Дифференциалдық геометрияның беттер теориясы

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 20 бет
Таңдаулыға:

Мазмұны

Кіріспе

1 Бет туралы ұғым
5
1.1 Беттің анықтамасы
5
1.2 Бет нүктелерінің ішкі координаталары
6
1.3 Беттегі қисықтар
7
2 Бетке жүргізілген жанама жазықтық және нормаль
8
2.1 Жанама жазықтықтың анықтамасы
8
2.2 Беттің нормалі
9
3 Беттің бірінші квадраттық формасы
12
3.1 Беттің бірінші квадраттық формасы және беттегі қисықтың ұзындығы
12
3.2 Беттегі қисықтардың арасындағы бұрыш
14
4 Беттің екінші квадраттық формасы
15
4.1 Беттің екінші квадраттық формасының анықтамасы
15
4.2 Беттегі қисықтың иілімі
18
5 Есептер
21
Қорытынды

Қолданылған әдебиеттер

Кіріспе
Менің курстық жұмысымның тақырыбы Дифференциалдық геометрияның беттер теориясы, есептері.
Беттер теориясы -- дифференциалдық геометрияның беттерінің қасиетін зерттейтін саласы. Классикалық беттер теориясында беттің қозғалыс кезінде өзгермейтін қасиеттері қарастырылады. Оның негізгі есептерінің бірі -- беттегі өлшеулер. Беттегі өлшеулердің көмегімен алынған фактілер жиынтығы беттің ішкі геометриясын құрайды. Сызықтың ұзындығы, екі бағыттың арасындағы бұрыш, сондай-ақ, геодезиялық сызық, геодезиялық сызықтың қисықтығы, т.б. ұғымдар беттің ішкі геометриясының ұғымдарына жатады.
Жалпы жағдайда беттің табиғаты сан алуан болып келеді. Сондықтан оны жазықтықтың бөлігінен деформация арқылы алу мүмкін емес. Олар өзін-өзі қиятын немесе беттескен бөліктері де бар болуы мүмкін. Дегенмен, мұндай беттің әрбір нүктесінің маңайының құрылымы элементарлық бет тәрізді болып келеді.
Беттердің геометриялық қасиеттерін зерттеу үшін оларға кейбір шарттар - регулярлық шартын қоямыз. Ерекшеліктері жоқ беттерді қарастыруымен ғана шектеліп қоймай және оларды зерттеу үшін тиімді тәсілдерді дамытып, біз беттердің кейбір маңызды сипаттамаларын: бетке жүргізілген жанама жазықытық және нормаль, бірінші және екінші квадраттық формалар және т.б. енгіземіз.
Соңғы кезде беттің классикалық теориясымен қатар, беттегі нүктенің жақын аймағын ғана емес, бетті тұтас қарастыратын теория да дамып келеді. Бұл теорияда регулярлы беттер де, ұшы не қыры бар беттер де зерттеледі.
Зерттеудің мақсаты: дифференциалдық геометрияның беттер теориясын талдау. Беттің бірінші және екінші квадраттық формасын қарастыру.
Зерттеудің міндеті: дифференциалдық геометрияның беттер теориясының бастапқы бөлімін қарастыру. Дифференциалдық геометрияның беттер теориясын есептер мен мысалдарда қарастыру.
Зерттеу әдістері: талдау нәтижесінде алынған мәліметтерді бақылап,
тақырып бойынша әдебиеттерді зерттеу.
Курстық жұмыстың құрылымы: курстық жұмыс кіріспеден, негізгі бөлімнен, практикалық бөлімнен, қорытынды және қолданылған әдебиеттер тізімінен тұрады.

1 Бет туралы ұғым
1.1 Беттің анықтамасы

Жай және регулярлық беттер. Біз бұдан былай R1,R2 евклидтік кеңістіктерді қарастырамыз.Бұл кеңістіктерде декарттық координаталар системалары берілген деп, яғни R2 кеңістігінің әрбір нүктесіне екі нақты сан, R3 кеңістігінің әрбір нүктесінде үш нақты сан сәйкестікке қойылған деп есептейміз. R2 кеңістігінің метрикасы ρ2 болсын. Онда R2 кеңістігінің ρ2(М0М)ε теңсіздігін қанағаттандыратын барлық М нүктелерінің жиынын, центрі М0 нүктесі, радиусы ε, ашық дөңгелек дейміз. Мұндағы ε - тұрақты, М0- берілген нүкте және М0∈R.
Анықтама. R2 кеңістігіндегі ашық дөңгелектің гомеоморфты бейнесі болатын, R3 кеңістігіндегі нүктелердің жиынын жай бет деп атаймыз.
G - деп R2 кеңістігіндегі ашық дөңгелекті белгілейік.
Р⊂R3 осы ашық дөңгелектің гомеоморфты бейнесі болсын.Онда бір f гомеоморфизмі табылып, f(G)=P. Келісуіміз бойынша R2,R3 кеңістіктерінде координаталар системасы берілген. Олай болса, f бейнелеуі (u,v)∊G нүктесіне (x,y,z)=P нүктесін сәйкестікке қояды. Яғни төмендегідей:

x=x(u,v)y=yu,vz=z(u,v) (u,v)∊G (2.1.1)

(2.1.1) теңдіктер системасын Р бетінің параметрлік теңдеуі деп атаймыз.
Ал, мына

r=ru,v,(u,v)∊G (2.1.2)

Теңдікті Р бетінің векторлық теңдеуі деп атаймыз. Егер Р беті (2.1.2) векторлық теңдеумен берілсе, онда Р: r=ru,v,(u,v)∊G деп жазалық. (2.1.1) функциялар G мен Р жиындарының арасында өзара бір мәнді сәйкестік орнатуы үшін

(хuyuzuxpyvzv) (2.1.3)

Матрицасының жиынының барлық нүктелеріндегі рангісі екіге тең болуы қажетті және жеткілікті екендігі матанализ курсынан белгілі. (2.1.3) матрицадағы Хu,...,Хv деп dxdu,...,dzdv дербес туындылар берілген. (2.1.3) матрицаның рангісі екіге тең болуы үшін ru,rv векторларының коллинеар болмауы қажетті және жеткілікті, яғни

ru,rv!=0 (2.1.4)

Беттің (2.1.4) қатысты қанағаттандырмайтын нүктелерін беттің ерекше нүктелері деп атайды.
Анықтама. Р: r=ru,v,(u,v)∊G беті берілсін. Егер бұл беттің ерекше нүктелері жоқ болса және ru,v векторлық функцияның барлық к - ретті үзіліссіз туындылары бар болса, онда Р беті к - ретті регулярлық бет деп аталады және

Р: r=ru,v∈СкG, k =1

деп жазады.
Қай ретте беттер z = z(x,y) түріндегі теңдеулермен берілуі мүмкін. Мұндай жағдайда бет айқын теңдеумен берілді деп айтады. Айқын теңдеумен берілген беттің теңдеуін (2.1.1) түрге келтіруге болады. Шынында да, егер x=u, y=v деп белгілесек, онда

x=u
y=v
z = (u, v)

шығады.
Егер бет F(x,y,z)=0 теңдеуімен берілсе,онда бет айқын емес түрде берілген деп айтады. Жалпы, соңғы теңдік, бетті анықтауы үшін Fx2x,y,z++Fy2x,y,z+Fz2x,y,z!=0 болуы керек, яғни дербес туындылардың біреуі нөлден өзгеше болуы қажет. Fz!=0 болсын. Онда F(x,y,z)=0 теңдігі Fz!=0 қанағаттандырып тұрған нүктенің мейлінше аз аймағында , z=z(x,y) функциясын анықтайтыны матанализ курсынан белгілі. Ендеше беттің теңдеуін айқын түрде жазуға болады.

1.2 Бет нүктелерінің ішкі координаталары
Бізге P:r=ru,v,(u,v)∈G беті берілсін. Онда беттің әрбір нүктесіне (u,v) қос саны сәйкес келеді. Яғни (u,v) қос саны осы нүктенің координаталарының ролін атқарып тұр. Осыған байланысты (u,v) қос санын, беттің нүктесінің ішкі немесе гаусстық координатасы деп атаймыз. Беттің теңдеуі және оның нүктесінің ішкі координаталары берілсе, онда ол нүктенің декарттық координаталарын табуға болады.

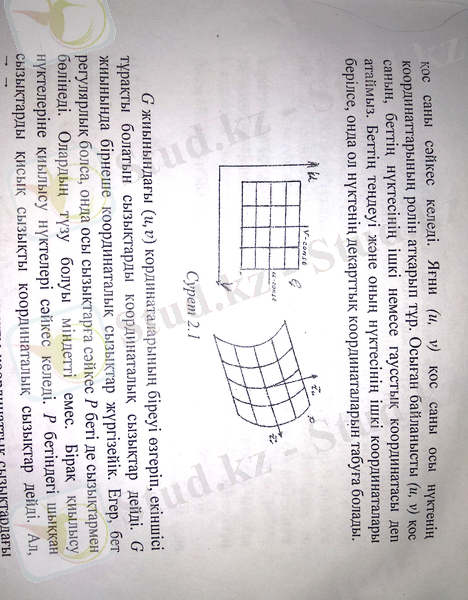
G жиынындағы (u,v) координаталарының біреуі өзгеріп, екіншісі тұрақты болатын сызықтарды координаталық сызықтар дейді. G жиынында бірнеше координаталық сызықтар жүргіейік. Егер, бет регулярлық болса, онда осы сызықтарға сәйкес Р беті де сызықтармен бөлінеді. Олардың түзу болуы міндетті емес. Бірақ қиылысу нүктелеріне қиылысу нүктелері сәйкес келеді. Р бетіндегі шыққан сызықтарды қисық сызықты координаталық сызықтар дейді. Ал, ru,rv векторлары - осы қисық сызықты координаталық сызықтардағы берілген нүктедегі сәйкес u=const, v=const сызықтарының бағытталған - жанамалары болады.

1.3 Беттегі қисықтар

Бізге P:r=r(u,v)∈CkG регулярлық беті берілсін. G жиынында жатқан, параметрік теңдеуі

u=ut,v=vt (2.1.5)
болатын l қисығын қарастыралық. Бұл қисық та k-ретті регулярлық қисық болсын. Онда P бетіндегі ішкі координаталары, (2.1.5) теңдікті қанағаттандыратын нүктелердің жиыны, P бетінде жатқан бір l қисығын береді және оның теңдеуі
r=rut,vt=r1t (2.1.6)
болады. Бұл қисық регулярлық қисық.

2 Бетке жүргізілген жанама жазықтық және нормаль
2.1 Жанама жазықтықтың анықтамасы
Бізге бір P регулярлық беті берілсін. M - осы P бетінің кез келген нүктесі болсын.
Анықтама. P бетінің M нүктесі арқылы өтетін, P бетінде жатқан барлық регулярлық қисықтардың M нүктесіндегі жанама түзулердің жиынын, P бетінің M нүктесіндегі контингенциясы деп атайды. Егер ол жазықтық болса, онда оны P бетінің M нүктесіндегі жанама жазықтығы деп атаймыз.
Mu0,v0 нүктесі арқылы өтетін, ruu0,v0,rvu0,v0 векторлары арқылы анықталатын жазықтықты PI деп белгілейік, PI бетке M нүктесінде жүргізілген жанама жазықтық болады.
M берілген нүкте, N жанама жазықтықтың ағым нүктесі болсын, онда MN,ru,rv векторлары компланар, яғни
MN,ru,rv=0 (2.2.1)
x0,y0,z0 үштігі М нүктесінің координаталары, ал X,Y,Z үштігі N нүктелерінің координаталары болсын. Онда (2.2.1) теңдік координаталар түрінде төмендегідей жазылады.
X-x0 Y-y0 Z-z0xuu0,v0 yuu0,v0 zuu0,v0xvu0,v0 yvu0,v0 zvu0,v0 =0 (2.2.2)
алып жазуға болады. Бұл параметрлік түрде берілген бетке жүргізілген жанама жазықтықтың теңдеуі.
Егер бет айқын түрде
z=zx,y
теңдеуімен берілсе, және x=u,y=v деп алсақ, (2.2.9) теңдіктен:
Z-z0=dzx0,y0dxX-x0+dzx0,y0dyY-y0 (2.2.3)
шығады.
Ал, енді бет айқын емес түрде,
Fx,y,z=0 (2.2.4)
теңдігімен берілсе, жанама жазықтықтың теңдеуі
FxX-x0+FyY-y0+FzZ-z0=0 (2.2.5)
болады.

2.2 Беттің нормалі
Анықтама. P:r=ru,v∈CkG, k=1 беті берілсін. Р бетінің М нүктесіндегі нормалі деп Р бетінің М нүктесіндегі жанама жазықтығына перпендикуляр және жанасу нүктесінен өтетін түзуді айтамыз.
Енді беттің нормалінің теңдеулерін қарастырайық. ru,rv векторлары жанама жазықтықты анықтап тұрған векторлар болғандықтан, олардың әрқайсысы нормальдің бағыттаушы вектор ru,rv болады. Егер ru,rv векторын координаталық түрде жазсақ былай болады:

ru,rv=yuzuyvzvMi+zuxuzvxvMj+xuyuxvy vMk. (2.2.6)

Мұндағы анықтауыштардың төменгі жағындағы М индекс анықтауыштың осы нүктеде есептелетінін көрсетеді. Mx0,y0,z0 болсын. X, Y, Z деп нормальдің ағым координаталарын белгілейік. Онда нормальдің канондық теңдеуін жазуға болады:

X-x0yuzuyvzvM=Y-y0zuxuzvxvM=Z-z0xuy uxvyvM (2.2.7)

Бет параметрлік, болмаса айқын түрде берілгенде бұл формуланы қолдануға болады.
Егер бет (2.2.11) түрде, яғни айқын емес түрде берілсе, нормаль теңдеуін:

X-x0Fxx0,y0,z0=Y-y0Fyx0,y0,z0=Z-z0F zx0,y0,z0 (2.2.8)

түрінде жазуға болады. Себебі Fx, Fy, Fz (2.2.13) жазықтықтың нормаль векторының координатасы. Олай болса, оны беттің нормалының бағыттаушы векторының бірі есебінде қарастыруға болады.
Анықтама. m=ru,rvru,rv векторын беттің бірлік нормаль векторы ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.