Аксиомалар системасының интерпретациясы

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 24 бет
Таңдаулыға:

Мазмұны

Кіріспе

1. Гильберт Давид өмірбаяны
5
2. Аксиоматикалық метод
7
2.1. Евклид геометриясының аксиоматикасы
7
2.2. I. Байланыс аксиомалары
8
2.3. II. Рет аксиомалары
10
2.4. III. Конгруэнттік аксиомалары
13
2.5. IV. Үзіліссіздік аксиомасы
15
2.6. V. Параллельдік аксиомасы
18
3. Аксиомалар системасының интерпретациясы
18
4. Аксиомалар системасын зерттеу
21
4.1. Үзіліссіздік аксиомасының тәуелсіздігі
25
Қорытынды

Қолданылған әдебиеттер

Кіріспе

Мен өзімнің курстық жұмысымда Геометрия аксиоматикасы тақырыбын қарастырамын.
Аксиома (көне грекше - лайықты қабылданған қағида) - нанымдылығы ақиқат (шындық) болғандықтан логикалық дәлелдеусіз алынатын қағида; теорияның ақиқат (шындық) ең бастапқы қағидасы. "Аксиома" термині Ертедегі Грекияда пайда болған. Ол алғаш рет Арситотельдің (біздің заманымыздан бұрын 384-322 жылдары) еңбектерінде кездеседі. Ал Евклид (біздің заманымыздан бұрын III ғасырда) аксиомалық жүйені пайдалана отырып өзінің басты еңбегі - "Негіздерді" жазды.
Математикалық теорияның негізі болып табылатын аксиомалар жүйесі де аксиомалар сияқты үнемі өзгертіліп әрі жетілдіріліп отырады. Аксиомалар жүйесіне оның қайшылықсыздығы, тәуелсіздігі және толықтығы сияқты негізгі талаптар қойылады. Аксиомалық тәсілдер геометрияда, арифметикада, ықтималдықтар теориясында тағы басқа салаларда кеңінен қолданылады.
Гильберттің ең маңызды ғылыми шығармаларының бірі Геометрияның негіздемесі атты еңбегі. Пиери еңбектері сияқты, Гильберттің бұл еңбегі 1899 жылы бірінші баспадан шыққан. Қазіргі аудармасы 1930 жылы жетінші баспадан бастап істеген. Осы еңбегінде Евклидтің геометриясының аксиомасының толық жүйесін берді. Гильберт жүйелі түрде өз аксиомаларының өзара тәуелсіздігін үйренеді және өзі іргелі геометриялық теоремалардың аксиомаларын жасады.
Гильберттің Геометрияның негіздемесі атты еңбегіндегі аксиоматикаға арналған бөлімінің алғы сөзінде былай деп жазылған Геометрия - арифметика сияқты өзінің құрастырған тек қана бір шама негізгі ережелерін талап етеді. Бұл негізгі ережелер геометриялық аксиомалар деп аталады. Геометриялық аксиомалардың анықталуы және олардың арақатынастарының зерттелуі Евклид заманындағы математикалық әдебиеттің көп ғажайып шығармаларының тақырыбы болып табылған.
Зерттеулердің жаңа талаптарын ескере отырып толық және оңай аксиомалар жүйесін геометрия үшін орнатуға болады, сонымен қатар ең маңызды геометриялық аксиомалармен теоремалар түсінікті болу үшін аксиомалардың әр түрлі топтарынан жеке аксиомалар пайда болды.
Мақсаты: Геометрия аксиоматикасын, теоремаларын, тұжырымдамалары мен системаларын толық қарастыру.
Міндеті: Геометрия аксиоматикасымен танысу, олардың салдарын, сызбаларын ажырата білу.

I. Гильберт Давид өмірбаяны
Гильберт Давид (нем. David Hilbert; 23 қаңтар 1862 -- 14 ақпан 1943) -- неміс математигі. Оның зерттеулері математиканың көптеген салаларының дамуына едәуір ықпал етті. Ол бүгінгі функционалдық талдаудың негізі болып табылатын Гильберттік кеңістіктер теориясын қалады. Оның 1899 жылы басылып шыққан "Геометрияның негіздері" деген кітабында геометрияны аксиомалық тұрғыда құруға арналса, 1934 - 1939 жылдар аралығында неміс математигі Пауль Бернайспен (1888 - 1977) бірігіп жазылған "Математиканың негіздері" атты еңбегінде бүкіл математиканы формалды түрге келтіруге әрекет жасалған. Ол математикалық теорияларды көрнекі түрде баяндаудың шебері болған. Осы тұрғыдан алғанда оның 1932 жылы француз математигі Стефан Кон-Фоссенмен (1902 - 1936) бірлесіп жазған "Көрнекі геометриясын" атауға болады. Оның "Табиғатты танып білу" деген мақаласы "Біздің білуіміз керек - біз білеміз де" деген ұранмен аяқталған. Ол 1900 жылы математиктердің дүниежүзілік конгресінде жасалған "Математикалық мәселелер" деген баяндамасында әріптестерін математиканың көптеген салалары бойынша шешімі табылмаған мәселелерді атап, оларды шешу ісіне атсалысуға шақырған.
Д. Гильберттің 1899 жылы жарыққа шыққан Геометрия негіздемелері деген кітабы ерекше әйгілі болды, оған 1903 жылы Н.И. Лобачевский атындағы халықаралық сыйлық берілді.
Геометрия әдетте аксиоматикалық әдіс негізінде құрылады. Ол қысқаша былай тұжырымдалады. Бір немесе бірнеше қатынаспен байланысқан кейбір объектілер енгізіледі. Бұл объектілер мен қатынастар негізгі деп аталады. Негізгі объектілер мен қатынастар аксиомалар талаптарын қанағаттандырғаны болмаса, табиғаты әртүрлі болуы мүмкін. Аксиомалар дәлелдемесіз қабылданатын тұжырымдар болып табылады. Аксиомалардан логикалық пайымдау арқылы туындайтын кез келген тұжырым теорема деп аталады. Берілген аксиомалар жүйесіне негізделген ұғымдар мен теоремалар жиынтығын, осы жүйеде салынған теория деп, ал осындай теорияларды салу әдісін аналитикалық әдіс дейді.
Гильберт ұсынған аксиомалар жүйесі 5 топтан тұрады: байланыс аксиомалары, рет аксиомалары, конгруэнттік аксиомалары, үзіліссіздік аксиомалары, параллельдік аксиомасы. Осы 5 топтың аксиомалары - нүкте, түзу және жазықтық атаулы үш текті объектіге және олардың арасындағы тиісті, арасында жатады және конгруэнтті сөздерімен өрнектелген үш қатынасқа қатысты. Нүкте, түзу және жазықтық дегеннің не екенін және көрсетілген қатынастардың тиянақты мағынасын Гильберт нақтыламайды. Олар жөнінде белгілі деп ұйғарылғанның барлығы аксиомаларда өрнектелген. Осының арқасында Гильберт аксиомалары негізінде салынған геометрия үйреншікті кескіндеуге тым алшақ түсіндірмелердің бар болуын мүмкін етеді.
Гильберт өзі ұсынған аксиомалар жүйесін терең әрі жан-жақты зерттеуден өткізді. Дербес жағдайда, егер арифметика қайшылықсыз болса, оның аксиомалар жүйесі қайшылықсыз екенін дәлелдеді. Онан соң Гильберт параллельдік аксиомасынан өзгеше, кейбір аксиомаларлың тәуелсіздігін дәлелдеді. Ақыр аяғы, Гильберт, геометрия негізіне, аксиомалар жүйесі бөлшектенген, қандай да аксиомалар тобын салғаннан, оны қалайша терең дамытуға болатыны жөніндегі сұрақты зерттеді.
Гильберттің жұмысымен элементар геометрия негіздемесі бойынша жүргізілген көпғасырлық зерттеулер негізінен аяқталды. Бұл жұмыс замандастары тарапынан жоғары бағаға иеленді және жоғарыда айтқанымыздай халықаралық жүлдемен марапатталды.

II. Аксиоматикалық метод

2.1. Евклид геометриясының аксиоматикасы

Математикалық теорияларды логикалық дәйектілік тұрғысынан қарастыру үшін ол теорияларға негіз болған аксиомалар системалары жеткіліксіз екендігі XIX ғасырдың екінші жартысында анықталды. Бұл жағдай әсіресе проективтік геометрия, евклидтік емес геометриялар, n-өлшемді кеңістіктер геометриялары құрылғаннан кейін айқын болды.
Осымен қатар математикалық теориялардың бірінің методтары екіншілерінде де қолданыла бастаған. Ал бір теорияның методтарын екінші бір теорияда пайдалану үшін алдымен сол теориялардың принциптерін, яғни логикалық негіздерін (аксиомалар системасын) зерттеу керек болады.
Міне осындай екі жағдай математика ғылымының аксиоматикалық метод жөніндегі теориясын туғызды.
Біз бұл тарауда геометрияның аксиоматикалық методын қарастырамыз. Аксиоматикалық методқа сүйеніп геометриялық теорияны құру мәселесін аксиомалар системасынан, яғни аксиоматикадан, бастаймыз. Бұл аксиомаларда геометриялық теорияның негізгі ұғымдары туралы сөз болады. Ол ұғымдар тек аксиомалар арқылы ғана анықталады, сондықтан оларды аксиомаларда ғана қанағаттандыратын геометриялық объектілер деп есептеуге тиістіміз.
Аксиомалардан логика заңдарына сүйеніп салдарлар, яғни теоремалар, қорытылып шығарылады. Дәлелденген теоремалар мен аксиомаларға сүйеніп басқа теоремалар дәлелденеді. Осылайша жаңа теоремалар пайда болады.
Сонымен, аксиомалар дегеніміз - геометрияның негізгі ұғымдары жөніндегі дәлелдемей алынған бастапқы ақиқаттар. Алдын ала берілген аксиомаларға сүйеніп теоремаларды дәлелдеу арқылы геометриялық теориялар (геометриялық системалар) құралады. Әрине, геометриялық теориялар берілген аксиомалар системасына байланысты, яғни аксиомалар системасын өзгертетін болсақ, бұл өзгеріске сәйкес геометриялық теория да өзгереді.
Аксиоматикалық методты зерттеп жасау мәселесіне еңбек сіңірген математиктер - Паш, Пеано, Веронезе, Гильберт. Әсіресе Д. Гильбертті ерекше атау керек, оның Геометрияның негіздері деген 1899ж. басылып шыққан классикалық еңбегінде Евклид геометриясының қайшылықсыз және толық аксиомалар системасы туралы баяндалады.
Енді Евклид геометриясының аксиомалар системасын келтірейік. (Бұл аксиомалар системасын Д. Гильберт құрған, сол себептен олар Гильберт системасы деп аталады).
Объектілердің немесе кез келген заттардың үш түрлі жиынын қарастырамыз. Бірінші жиын объектілерін нүктелер деп, екінші жиын объектілерін түзулер деп, ал үшінші жиын объектілерін жазықтықтар деп атауға келісейік. Нүктелер, түзулер және жазықтықтар бір-бірімен үш түрлі қатынаста болуы мүмкін деп ұйғарайық. Ол қатынастарды байланыс, реттік, конгруэнттік (немесе теңдік) қатынастары деп атайық.
Негізгі объектілер (яғни нүктелер, түзулер, жазықтықтар және олардың арасындағы байланыс, реттік, конгруэнттік қатынастар) төменде келтірілген аксиомалардың шарттарын қанағаттандыруға тиіс. Евклид геометриясының аксиомалары бес топқа бөлінеді, олар:
I - байланыс аксиомалары,
II - рет аксиомалары,
III - конгруэнттік аксиомалары,
IV - үзіліссіздік аксиомасы,
V - параллельдік аксиомасы.
Ілгеріде нүктелерді А, В, С, ... , түзулерді a, b, c, ... , жазықтықтарды α, β, γ, ... әріптерімен, байланыс қатынасын H таңбасымен, реттік қатынасын :: таңбасымен, конгруэнттік қатынасын ≡ таңбасымен белгілеуге келісейік те, әр топтың аксиомаларын өз алдына қарастырайық.

2.2. I. Байланыс аксиомалары

Бірінші топ аксиомалары байланыс қатынасын анықтайды. Нүктелер түзулермен (не жазықтықтармен) байланыс қатынасында болуы мүмкін. Егер А нүктесі а түзуімен байланыс қатынасында болса, онда а түзуі А нүктесі арқылы өтеді немесе А нүктесі а түзуінің бойында жатады дегенге келісейік. Егер екі түзу бір А нүктесі арқылы өтетін болса, онда олар сол А нүктесінде қиылысады, яғни А нүктесі сол түзулердің ортақ нүктесі болады дейміз. Нүктелер мен жазықтық арасындағы байланыс қатынасы жөніндегі келісімдер де жоғарыдағыша тұжырымдалып айтылады.
Егер а түзуінің əр нүктесі α жазықтығында жатса, онда а түзуі α жазықтығында жатады дейміз.
Ілгеріде нүктелер ( түзулер, жазықтықтар) дегенде, əр түрлі нүктелер ( түзулер, жазықтықтар) туралы сөз болатындығын ескереміз.
Енді бірінші топ аксиомаларын келтірейік.
I1. Кез келген А мен В екі нүкте арқылы өтетін а түзуі болады.
I2. Кез келген А мен В екі нүкте арқылы өтетін а түзуі біреуден артық болмайды.
I3. Әрбір түзудің бойында кемінде екі нүкте жатады.
Бір түзудің бойында жатпайтын кемінде үш нүкте болады.
I4. Бір түзудің бойында жатпайтын кез келген үш нүкте арқылы өтетін жазықтық болады.
Әрбір жазықтықта кемінде бір нүкте жатады.
I5. Бір түзудің бойында жатпайтын кез келген үш нүкте арқылы өтетін жазықтық біреуден артық болмайды.
I6. Егер түзудің екі нүктесі бір жазықтықта жатса, онда ол түзудің әрбір нүктесі де сол жазықтықта жатады.
I7. Егер екі жазықтықтың бір ортақ нүктесі болса, онда олардың кемінде тағы да бір ортақ нүктесі болады.
I8. Бір жазықтықта жатпайтын кемінде төрт нүкте болады.
Байланыс аксиомалары сүйеніп дәлелденетін теоремалар онша көп емес. Солардың кейбіреулерін келтірейік.
Теорема. Екі түзудің тек қана бір ортақ нүктесі болуы мүмкін.
Әр түрлі a мен b түзулерінің екі ортақ нүктесі болсын делік. Олай болғанда I2 аксиома бойынша a мен b түзулері әр түрлі болмай шығады. Бұл теореманың шартына қайшы.
Теорема. Әр түрлі екі жазықтықтың не бірден-бір ортақ нүктесі болмайды, не олардың ортақ түзуі болып, жазықтықтардың барлық ортақ нүктелері осы түзудің бойында жатады.
Шынында, α мен β жазықтықтарының ортақ А нүктесі болсын. I7 аксиома бойынша олардың кемінде тағы бір ортақ В нүктесі болады. А мен В нүктелері бір а түзуін анықтайды (I2 аксиома). I6 аксиома бойынша а түзуі α жазықтығында да, сондай-ақ β жазықтығында да жатады, яғни а түзуі α мен β жазықтықтарына ортақ.
Енді а түзуінің бойында α мен β жазықтықтарының барлық ортақ нүктелері жататындығын дәлелдейік.
Қарсы жориық, яғни α мен β жазықтықтарының ортақ С нүктесі болып, ол нүкте α түзуінің бойында жатпасын. Ал әр түрлі А, В, С үш нүкте арқылы өтетін жазықтық біреуден артық болмайды (I5 аксиома). Ендеше α мен β бірігіп бір жазықтық болу керек, бірақ теореманың шарты бойынша α мен β әр түрлі жазықтықтар. Демек, біздің α мен β жазықтықтарының ортақ С нүктесі а түзуінің бойында жатпайды деген жоруымыз дұрыс емес. Сонымен, теорема толық дәлелденді.
Келесі теоремалардың дәлелдемесін келтірмейміз, оларды оқушылардың өздері де дәлелдей алады.
Теорема. Берілген жазықтықта жатпайтын түзумен сол жазықтықтың не ортақ нүктесі болмайды, не олардың жалғыз ғана ортақ нүктесі болады.
Теорема. а түзуі мен ол түзудің бойында жатпайтын А нүктесі берілсе, онда А нүктесі мен а түзуі арқылы жалғыз ғана жазықтық жүргіуге болады.
Теорема. Әрбір жазықтықта бір түзудің бойында жатпайтын кемінде үш нүкте болады.

2.3. II. Рет аксиомалары

Екінші топ аксиомалары реттік қатынасты анықтайды. Біз реттік қатынасты бір түзудің бойында жатқан нүктелер үшін ғана қарастырамыз. Егер бір түзудің бойында жатқан В нүктесі А және С нүктелерімен реттік қатынаста болса, онда В нүктесі А мен С нүктелерінің арасында жатады дейтін боламыз.
II1. Егер В нүктесі А мен С нүктелерінің арасында жатса, онда А,В және С нүктелері бір түзудің әр түрлі үш нүктесі болады және В нүктесі С мен А нүктелерінің арасында жатады.
II2. Егер А мен В бір түзудің нүктелері болса, онда сол түзудің бойынан мынадай қасиеті бар кемінде бір С нүктесі табылады: В нүктесі А мен С нүктелерінің арасында жатады.
II3. Түзудің кез келген үш нүктесінің ішінде қалған екі нүктесінің арасында жататын нүкте бірден артпайтын болады.
Төртінші аксиоманы келтіруден бұрын кейбір анықтамаларды берейік.
А мен В екі нүктенің жиынын АВ кесіндісі дейді; А мен В нүктелерін АВ кесіндісінің ұштары дейді. Бұл А мен В нүктелерінің арасындағы нүктелердң АВ кесіндісінің ішкі нүктелері немесе АВ кесіндісінің нүктелері дейді.
II4 (Паш аксиомасы). А,В және С - бір түзудің бойында жатпайтын үш нүкте болсын, а түзуі АВС жазықтығындағы осы нүктелердің ешқайсысы арқылы өтпейтін түзу болсын. Сонда егер а түзуі АВ кесіндісінің бір нүктесі арқылы өтетін болса, онда ол АС не ВС кесіндісінің бір нүктесі арқылы өтеді.

Байланыс және рет аксиомаларынан бірсыпыра салдар шығады. Негізінде екінші топ аксиомалары арқылы түзу бойындағы нүктелерді реттеуге болады. Рет аксиомаларын пайдаланып, сәуленің, бұрыштың, жарты жазықтықтың анықтамаларын беруге болады. Рет аксиомаларынан шығатын барлық теоремаларға тоқтамай, кейбір теоремаларды ғана келтірейік.
Теорема. АС түзуінің А мен С екі нүктесінің арасында жататын кемінде бір D нүктесі болады.
Расында да, I3 аксиома бойынша АС түзуінен тыс кемінде бір Е нүктесі болады; II2 аксиома бойынша АЕ түзуінің бойынан, Е нүктесі AF кесіндісінің нүктесі болатындай, F нүктесі табылады (7-сызба).

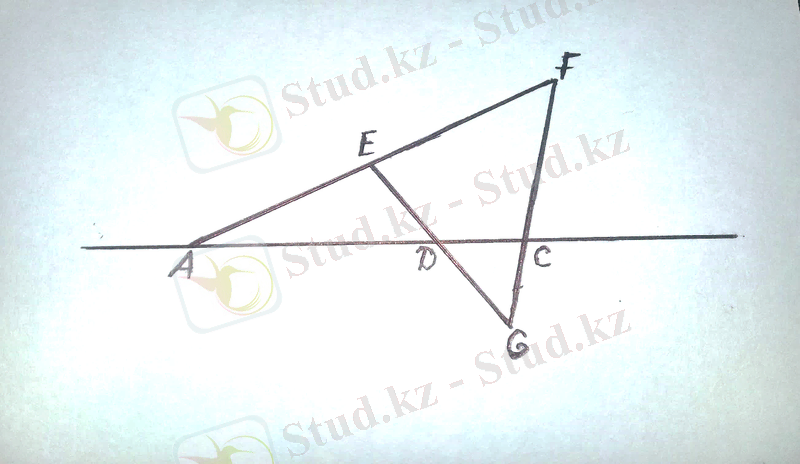
7-сызба
Сол II2 аксиома бойынша FC түзуінің бойынан C нүктесі F пен бір G нүктесінің арасында жататындай С нүктесі табылады. Ал II3 аксиома бойынша G нүктесі F пен С-нің арасында жатпайды, яғни G нүктесі FС кесіндісінің нүктесі емес. Паш аксиомасынан A, F және С нүктелері мен EG түзуіне қолдансақ: EG түзуі не АС кесіндісінің не FС кесіндісінің ішкі нүктесі арқылы өтуі керек. Алайда EG түзуі FС кесіндісін қия алмайды, себебі, онда I1 және I2 аксиомалар бойынша, бұл қарастырылып отырған нүктелер бір түзудің бойында жататын болып шығады. Ал, А, С және Е нүктелері бір түзудің бойында жатпайды. Сондықтан EG түзуі АС кесіндісін бір D нүктесінде қияды. Сонымен, теорема дәлелденді.
Басқа теоремаларды дәлелдемесіз келтірейік.
Теорема. Түзудің екі нүктесінің арасында шексіз көп нүктелер болады.
Теорема. Егер С мен D нүктелері А мен В нүктелерінің арасында жатса, онда CD кесіндісінің барлық нүктелері де АВ кесіндісінің нүктелері болады.
Бұл жағдайда CD кесіндісі АВ кесіндісінің ішінде жатады дейді.
Теорема. а түзуінің кез келген О нүктесі ол түзудегі нүктелерді екі жинаққа бөледі де, А мен В түрлі жинақтардың нүктелері болса, О нүктесі А мен В-нің арасында жатады, ал А мен В бір жинақтың нүктелері болса, О нүктесі А мен В-нің арасында жатпайды.
Анықтама. а түзуіндегі нүктелердің О нүктесімен анықталатын екі жинағының әрқайсысы түзудің жарты түзулері, немесе сәулелері, деп аталады. О нүктесін сәуленің бас нүктесі дейді.
Осы келтірілген анықтамалар мен теоремаларға сүйеніп, түзу нүктелерін екі жолымен реттеуге болады. Реттеу тәсіліне байланысты түзудің бағыты анықталады. Сонымен, түзуді екі бағытта қарастыруға болады. Оларды түзудің қарама-қарсы бағыттары дейді.
Теорема. α жазықтығындағы кез келген а түзуі сол жаықтықтағы нүктелерді екі жинаққа бөледі: егер де А мен В түрлі жинақтардың нүктелері болса, АВ кесіндісі а түзуін қияды; ал, егер де А мен В бір жинақтың нүктелері болса, АВ кесіндісі а түзуін қимайды.
Анықтама. α жазықтығындағы нүктелердің а түзуінің анықталатын екі жинағының әрқайсысы сол α жазықтығының жарты жазықтығы деп аталады.
Конгруэнттік аксиомаларын келтіргенде бұрыш деген ұғыммен пайдаланамыз. Сол себептен бұрыштың анықтамасымен танысайық.
Анықтама. Ортақ О төбесі бар әр түрлі h және k екі сәулесін бұрыш деп атайды да, ∠(h,k) деп белгілейді, О нүктесін ∠(h,k) бұрышының төбесі деп, ал h пен k сәулелерін ∠(h,k) бұрышының қабырғалары дейді. Бұрыштарды бір әріппен (немесе үш әріппен) белгілейді: мысалы, ∠B немесе ∠ABC.

2.4. III. Конгруэнттік аксиомалары

Конгруэнттік аксиомалары конгруэнттік немесе теңдік қатынасын анықтайды. Конгруэнттік қатынастар кесінділер (бұрыштар) үшін қарастырылады.
III1. А мен В бір а түзуінің нүктелері болсын, А'- кез келген h сәуленің бас нүктесі. Сонда АВ≡А'B' шартты қанағаттандыратын h сәуленің бойында B' нүктесі болады. Басқаша айтқанда, бұл аксиома бойынша берілген АВ кесіндісінде тең етіп, берілген сәуленің бойына А' нүктесінен бастап, А'B' кесіндісін салуға болады.
III2. Егер де А'B'≡АВ және А''B''≡АВ болса, онда А'B'≡А''B''; басқаша айтқанда, екі кесінді бір кесіндіге конгруэнт болса, олар өз ара да конгруэнт болады.
III3. А,В,С нүктелері а түзуінің үш нүктесі болсын. В нүктесі А мен С нүктелерінің арасында жатсын, А',B',С' нүктелері осы а түзуінің немесе басқа бір а' түзуінің нүктелері болып, В' нүктесі А' пен С' нүктелерінің арасында жататын болсын; сонда, егер де АВ≡А'B', ВС≡В'С' болса, онда АС≡А'С' болады.
Анықтама. Бір а сәулесін h деп белгілейік; а түзуімен анықталатын жарты жазықтық λ болсын. Сонда h сәулесі мен λ жарты жазықтығын репер дейді, h сәулесінің бас нүктесі репердің бас нүктесі делінеді; а түзуін репердің түзуі, λ жарты жазықтығымен анықталған жазықтықты репердің жазықтығы дейді. h сәулесі мен λ жарты жазықтығы арқылы анықталған репердің (h,λ) деп белгілейді.
III4. α жазықтығындағы ∠(h,k) бұрыш берілсін; ∠(h',k')- кез келген репер болсын (дербес жағдайда h' сәулесі α жазықтығында жатуы мүмкін). Сонда λ' жарты жазықтығында ∠(h,k)≡∠(h',k') шартты қанағаттандыратын жалғыз ғана k' сәулесі болады.
Әрбір бұрыш өзіне конгруэнт болады.
III5. А,В,С бір түзудің бойында жатпайтын үш нүкте, ал А',B',С' нүктелері де бір түзудің бойында жатпайтын үш нүкте болсын. Сонда АВ≡А'B', АС≡А'С', ∠ВАС≡B'А'С' болса, ∠АВС≡А'B'С' болады.
Байланыс аксиомалары мен рет аксиомаларына және конгруэнттік аксиомаларына сүйеніп дәлелденетін кейбір теоремаларды келтірейік. Әууелі мынадай анықтаманы келтірейік.
Анықтама. А,В,С және А',B',С' үшбұрыштарында АВ≡А'B', АС≡А'С',ВС≡В'С',∠А≡А',∠В≡В',∠С≡С' болса, онда мұндай үшбұрыштар конгруэнт үшбұрыштар болады.
Теорема. Егер АВ≡А'B', АС≡А'С',∠А≡А' болса, онда А,В,С үшбұрышы А',B',С' үшбұрышына конгруэент болады.
Дәлелдеме. III5 аксиома бойынша АВ≡А'B', АС≡А'С', ∠ВАС≡B'А'С', сондықтан ∠АВС≡А'B'С', яғни ∠В≡В'. Сондай-ақ, АС≡А'С', АВ≡А'B', , ∠САВ≡С'А'В' болғандықтан, АСВ≡А'С'B', яғни ∠С≡С'. Енді ВС≡В'С' болатындығын байқау керек. Мұны қарсы жору жолымен дәлелдейік. ВС≢В'С'делік. В'С' сәулесінің бойынан ВС≡В'С* шартты қанағаттандыратын С* нүктесін табайық (III1 аксиома). А',B',С' нүктелері бір түзудің бойында жатпағандықтан, А',С*,С' нүктелері де бір түзудің бойында жатпайды, сондықтан (А'С') және (А'С*) сәулелер бір-бірімен беттеспейді. А'B' түзуі мен С' нүктесі арқылы анықталатын жарты жазықтықты λ деп белгілейік, С*≭ --λ, яғни С*нүктесі λ жазықтығындағы нүкте, сондықтан А'С'--- λ және А'С*--- λ. III5 аксиоманы қолдансақ, ВА≡B'А', ВС≡В'С*, ∠АВС≡А'B'С* болғандықтан, ∠ВАС≡B'А'С*. Бірақ жоғарыда , ∠ВАС≡B'А'С' екендігін байқағанбыз. Бұл III4 аксиомаға қайшы: λ жарты жазықтығында бір ВАС бұрышына конгруэнт болатын екі бұрыш B'А'С' және B'А'С* бұрыштары табылады.
Мына теореманы дәлелдеусіз келтіре кетейік.
Теорема. А,В,С және А',B',С' үшбұрыштарында: АВ≡А'B', ∠В≡В', ∠А≡А' болса, онда ол үшбұрыштар конгруэнт болады.
Конгруэнттік аксиомаларын пайдаланып, кесінділерді (немесе бұрыштарды) салыстыруға болады.
Анықтама. Конгруэент емес А1А2 және В1В2 екі кесінді берілсін. Бір О нүктесінен кез келген h сәулесін алып, соның бойына ОА≡А1А2, ОВ≡В1В2 кесінділерін салайық, А нүктесі О мен В нүктелерінің арасында болса, яғни ОАВ болса, онда А1А2 кесіндісі В1В2 кесіндісінен кем болады немесе В1В2 кесіндісі А1А2 кесіндісінен артық болады.
Бұрыштарды да осылайша салыстыруға болады.
Теорема. Үшбұрыштың сыртқы бұрышы өзімен сыбайлас емес ішкі бұрыштың қай-қайсынан да артық болады.
Конгруэнттік қатынастың қасиеттеріне сүйеніп, қозғалыстың геометриялық түсінігін қарастыруға болады.
Анықтама. Екі фигураның (нүктелер жинақтарының) нүктелерінің арасында өз ара бір мәнді сәйкестік болсын. Сонда сәйкестік кесінділер конгруэнт болса, онда ол фигуралар конгруэнт болады дейді, сонымен қатар бәр фигура екінші фигурадан ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.