Векторлық кеңістіктің қосымшалары

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 22 бет
Таңдаулыға:

Кіріспе
3

1
Вектор ұғымы
4
2
Векторларға сызықтық амалдар қолдану
5
3
Векторлық кеңістіктің негізгі теориялық мазмұны
8
4
Вектордың берілген базиске қарағанда координаттары және олардың қасиеттері
9
5
Кез келген екі векторлық кеңістіктің арасындағы изоморфизм
10
6
Векторлық кеңістіктің ішкі кеңістігі.
Алмастырулар туралы Штейниц теоремасы
11
7
Векторлық кеңістіктің сызықты көрінісі
16
8
Векторлық кеңістіктің қосымшалары
18
9
Есептер
19

Қорытынды
21

Қолданылған әдебиеттер тізімі
22

Мазмұны

Кіріспе
ХІХ ғ сызықтық теңдіктер жүйесінің теориясымен бірге векторлар теориясы да дамыған. Бағытталған кесінділерді Арган (J.Argand, 1768-1822) 1806 жылы жарияланған Жалған шамалардың бірқатар көрінісінің тәжірибесі атты жұмысында пайдаланған. Ол кесінділерді Арган а, b және т.б. белгілерімен белгілеген. Мебиус басы А нүктесі және соңы В нүктесі кесіндісін АВ белгісімен белгілеген. Ол векторлар теориясын құрушылардың бірі болып табылады. Вектор терминін Гамильтон шамамен 1845 жылы енгізген. Ол сондай-ақ 1863 жылы векторлардың скалярлық және векторлық туындыларын анықтаған. Бүл туындыларды Грасманның еңбектерінде 1844 жылдың өзінде көрсетілгенін атап көрсету қажет. Ол оларды ішкі және сыртқы туындылар деп атаған. Вектор интуициялық тараптан шамасы, бағыты және (міндетті емес) жету нүктесі бар нысан ретінде түсініледі. Векторлық санақ бастамалары кешенді сандардың геометриялық үлгісімен бірге пайда болды (Гаусс, 1831). Векторлармен дамыған операцияларды Гамильтон өзінің кватернионды есептерінің бөлігі ретінде (вектор кватерионның жалған бөлшектерін құраған) жариялаған. Гамильтон вектор (лат. Vector, тасымалдаушы) терминінің өзін ұсынды және векторлық анализдің кейбір операцияларын сипаттады. Ол түсінікті Максвелл өзінің электромагнетизм бойынша еңбектерінде пайдаланып, өзінің есептеріне ғалымдардың назарын аударды. Сәл уақыттан кейін Гиббстің Векторлық анализдің элементтері жарық көрді (1880 жж), ал біраздан кейін Хевисайд (1903) векторлық анализге заманауи сипат берді.
Бұл курстық жұмыстың негізгі бөлімінде вектордың негізгі теориялық мазмұны, вектордың базиске қарағанда координаттары мен олардың қасиеттері, кез келген екі векторлық кеңістіктің арасындағы изоморфизм, векторлық кеңістіктің ішкі кеңістігі, Алмастырулар туралы Штейниц теоремасы және векторлық кеңістіктің сызықты көрнісі жайында толық айтылған. Ал екінші бөлімінде векторлық кеңістіктің қосымшалары яғни векторлық кеңістіктің геометрия, физика, математика, астрономияда қолданылуы жайында айтылған. Және міндетті түрде практикалық бөлімде векторлық кеңістікке байланысты шығарған есептер бар.

1.Вектор ұғымы
Өзінің сандық мәнімен қоса кеңістіктегі бағытымен де сипатталатын шамалар векторлық шамалар немесе векторлар деп аталады.
Сонымен, орын ауыстыру векторлық шама болып табылады. Векторларды бағытталған кесінді түрінде кескіндейді және бір әріппен немесе вектордың басы мен ұшын көрсететін екі әріппен белгілеп, төбесіне нұскама (стрелка) қояды. Мысалы жылдамдық векторын ʋ немесе АВ, күш векторын F немесе CD түрінде кескіндеуге болады.
Кеңістікте белгілі бір бағыты болмайтын, тек сандық мәнімен ғана сипатталатын шамалар скалярлық шамалар немесе скалярлар деп аталады. Мысалы, уақыт, заттың тығыздығы, дененің көлемі, температура, арақашықтығын (орын ауыстыру емес), сынып бөлмесінің ұзындығы, ені және биіктігі, т.с.с. скалярлық шамаларға жатады.
Кез келген вектордың сандық мәні оның модулі деп аталады.Модуль -- скалярлық шама.
Егер a және b векторларының модульдері мен бағыттары бірдей болса, онда олар тең болады а = b. Ал векторлардың модульдері тең болып, бірақ бағыттары қарама-қарсы болса, онда а = - bболады.
1-анықтама. Вектор дегеніміз - бағытталған кесінді немесе қайсысы бірінші (басы), ал қайсысы екінші (ұшы) екендігі көрсетіліп берілген нүктелер жұбы.
Вектор ұзындығымен және бағытымен анықталған геометриялық объект. Егер вектор басы А нүктесі және ұшы В нүктесі арқылы берілетін болса, онда оны АВ деп белгілейді. Көпшілік жағдайда, вектор бір ғана әріппен белгіленеді, мысалы А,В,С т.с.с.
2-анықтама. Вектордың модулі немесе ұзындығы деп оның басы мен ұшының ара қашықтығын айтады. Кейбір жағдайларда вектордың ұзындығы оның абсолют шамасы деп те атайды. Вектордың модулі АВ немесе а деп белгіленеді.
3-анықтама. Егер екі немесе одан да көп векторлардың бастары бір нүктеде түйіскен болса, ондай векторлар үйлескен деп аталады (1.1а-сурет).
4-анықтама.Вектордың бас нүктесі мен соңғы нүктесі үйлескен болса, ол вектор нөльдік вектор деп аталады. Нөльдік вектордың бағыты анықталмаған, яғни кез келген бағытты қабылдайды. Нөльдік векторды 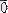түрінде белгілейміз.
Ескерту: Қарастырылатын а векторының бас нүктесі үшін кеңістіктегі немесе жазықтықтығы кезкелген нүктені (қажеттілігіне қарай) алуға болады. Сондықтан, олар да бос немесе ерікті векторлар деп атайды. Алдағы уақытта қарастырылатын векторларды ерікті векторлар деп түсіну қажет.
5-анықтама.Бір түзудің немесе параллель түзулердің бойында жатқан векторлар өзара коллинеарлы деп аталады
6-анықтама.Өзара коллинеарлы, ұзындықтары мен бағыттары бірдей а және в векторлары тең векторлар деп аталып, 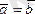түрінде жазылады
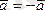
7-анықтама. Өзара коллинеарлы, ұзындықтары бірдей, ал бағыттары әр түрлі, және а векторлары қарама-қарсы векторлар деп аталады және 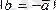түрінде жазылады.
8-анықтама.Векторлардың біреуін екіншісімен дәл келгенше бұрғандағы ең кіші айналу бұрышын (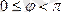) сол екі вектордың арасындағы бұрыш деп атайды. Аралық бұрыш, векторды сағат тіліне қарсы бағытпен айналдырудан шыққан болса оң, ал сағат тілімен бағыттас айналдырудан шыққан болса теріс болады.
10-анықтама.Векторлар бір жазықтыққа параллель болса, онда олар компланар векторлар деп аталады.

2.Векторларға сызықты амалдар қолдану

Векторларға сызықты амалдар қолдану қатарына, векторларды қосу, азайту және векторды нақты санға көбейту амалдары жатады.

Векторларды қосу

Мысалы, кез келген а және b векторлары берілсін. Осы векторларды қосып, a + b-ға тең болатын с векторын табу керек. Ол үшін векторды өзіне-өзін параллель көшіргенде вектор өзгермейді дейтін ережені пайдаланамыз. Осы ереженің көмегімен векторларды қосудың бірнеше тәсілдерін көрсетуге болады.

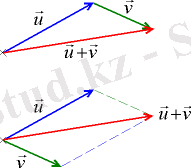
Мысалы, екі векторды бастарын түйістіре параллелограмның екі қабырғасы болатындай етіп өз-өзіне параллель көшіреміз де, параллелограмм саламыз. Сонда екі вектордың шыққан нүктесінен жургізілген бағыты көрсетілген диагональ қорытқы вектор болып табылады . Векторларды осылайша қосу параллелограмм ережесі бойынша қосу деп аталады.
Векторларды қосуда үшбұрыш ережесін де қолдануға болады. Ол үшін берілген векторларды бірінші вектордың ұшы екінші вектордың басымен түйісетіндей етіп, өз-өзіне параллель көшіреміз. Сонда бірінші вектордың басынан екінші вектордің ұшына қарай жүргізілген вектор сол екі вектордың қосындысын береді.
Ал енді екеу емес, бірнеше векторды қосу керек болса. Онда векторларды, алдыңғы вектордың ұшына келесі вектордың басы жалғасатындай етіп, әркайсысын параллель көшіреміз. Сонда алынған көпбұрыштың басы мен ұшын тұйықтап тұрған R векторы қорытқы вектор болып есептеледі. Ол бірінші вектордың басынан соңғы вектордың ұшына қарай бағытталады және мынаған тең болады: R = Ғ1+Ғ2+Ғ3+ Ғ4.
Екі u, v векторлары және олардың қосындысы
Екі векторларды қосуды параллелограмм ережесімен де, үшбұрыш ережесімен де іске асыруға болады.
Үшбұрыш ережесі. Екі 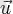мен 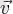векторларын үшбұрыш ережесімен қосу үшін осы екі векторды өздеріне біреуінің бас жағы екіншісінің аяғымен беттесетіндей параллель көшіру керек. Сонда пайда болған үшбұрыштың үшінші қабырғасы бас жағы алғашқы вектордың басымен беттесетін бастапқы екі вектордың қосынды векторы болып табылады.
Параллелограмм ережесі. Екі 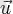мен 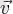векторларын параллелограмм ережесімен қосу үшін екеуін де бастары беттесетіндей параллель көшіріп параллелограммға болықтырады. Сонда екеуінің қосындысы деп параллелограммның осы екі вектор бас жағынан шығатын диагоналін айтады.
Екі сырғанақ векторларды қосу тек қана олар жатқан екі түзу қиылысқанда ғана анықталған. Бұл жағдайда әр вектор өз түзуі бойымен қиылысу нүктесіне дейін көшіріліп, содан кейін параллелограмм ережесімен қосылады.
Екі тұрақты векторларды қосу тек егер олардың ортақ бас нүктесі болғанда ғана анықталған. Бұл жағдайда да олар параллелограмм ережесімен қосылады.

Коллинеар сырғанақ векторларды қосу

Егер екі сырғанақ векторлар параллель болса, онда қосындыны табу қиыншылығы қосынды вектор жатқан түзуді табудың қиындығында жатыр. (Қосынды вектор бағыты мен ұзындығын еркін векторларды қосқандағыдау анықтаған абзал болар еді.) механикада статиканы зерттегенде параллель, еркін векторлармен берілетін, күштерді қосу мәселесінде қосымша гипотеза беріледі: берілген векторлар жүйесіне осы векторлар жатқан түзулерді қиып өтетіндей ұзындықтары бірдей, бағыттары қарама-қарсы бір түзу бойында жататындай екі векторды қосуға болады. Мысалы, параллель түзулерде жататын сырғанақ екі 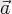және 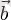внкторларын қосу керек болсын. Оларға бір түзу бойындағы 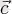мен векторларын қосайық. 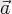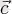мен векторлары жатқан түзулер қиылысады, сондықтан 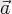мен векторлары да қиылысады. Яғни, келесі векторлар анықталған

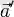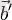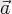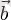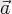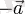мен векторлары жатқан түзулер мен векторлары шамалары бойынша тең бірақ бағыттары қарама-қарсы болғанда ғана қиылыспайды, бұл жағдайда мен векторлары -- векторлар жұбы деп аталады.
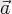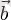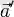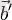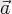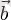Сонымен қорыта айтса, және векторларының қосындысы деп мен векторларының қосындысын түсіну керекі және бұл қосынды мен векторлары жұп болмаған жағдайдың бәрінде дұрыс анықталған.

Векторларды азайту

Векторларды косу ережесінен векторларды азайту ережесін шығарып алуға болады. Мысалы, с = а - b векторын табу керек болсын. Бұл теңдікті с = a + ( - b) түрінде жазуға болады, яғни векторлардың айырымын табу үшін а азайғыш векторға модулі азайткыш векторға тең, бірақ оған карама-карсы бағытталған - b векторын қосу керек. Немесе екі векторды өздеріне параллель көшіріп, бастары бір нүктеден шығатындай етіп орналастырамыз. Содан соң олардың ұштарын азайтқыштан (b) азайғышка (a) қарай бағытталған вектормен қосамыз. Міне, осы с векторы қорытқы вектор болады.

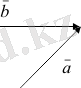
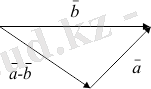
Бір тузудің бойында жатқан немесе бір-біріне параллель

Бір түзудің бойында жатқан немесе бір-біріне параллель векторлар бір жаққа қарай не қарама-қарсы бағытталуы мүмкін.
Мұндай векторлар а және b векторлары сияқты қосылады, яғни бірінші вектордың ұшы екінші вектордың басымен қосылады. Қорытқы вектор модулі бойынша қосылатын векторлар модульдерінің арифметикалық қосындысына немесе арифметикалық айырымына тең. Қорытқы вектор қосылатын векторлармен бағыттас модулі үлкен вектор жаққа қарай бағытталады.

Векторларды скалярға көбейту (бөлу)

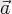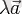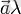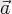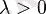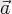векторы мен λ санының көбейтіндісі леп деп (немесе ) беліленетін, модулі тең, ал бағыты векторының бағытымен бірдей, егер болса. Егер , немесе вектор нөлдік болса, тек осы жағдайда ғана көбейтінді де 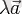-- нөлдік вектор.
Әдетте бұл көбейтіндіні жазғанда бірінші санды сосын векторды жазады, дегенмен де керісінше жазу да қате емес. Қалай десек те, .
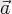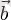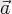
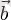
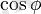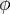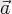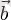мен векторларының көбейтіндісі деп тең санды айтады, мұндағы -- мен векторлары арасындағы бұрыш. Белгілеулері: 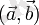немесе .
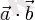Егер векторлардың біреуі нөлдік болса ϕ бұрышының беймәлімдігіне қарамастан көбейтінді нөлге тең боп деп есептеледі.
Векторлардың скаляр көбейтіндісінің қасиеттері:
1. -- коммутативтілік.
2. -- дистрибутивтілік.
3. -- санға көбейтуге қатысты сызықтық қасиеті.
4. -- вектор нормасы.
Геометриялық түрде алғанда скаляр көбейтінді бір вектордың ұзындығын екінші вектордың біріншісінің бағытына ортогональ проекциясының ұзындығын көбейткенге тең. Кез келген 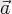векторының бірлік вектормен скаляр көбейтіндісі 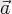векторының сол бірлік векторға ортогональ проекциясы болып табылады.
a векторынының b векторына Векторлық көбейтіндісі деп келесі шартты қанағаттандыруды айтады:
c векторының ұзындығы a мен b векторларының ұзындықтарының және осы векторлардың арасындағы φ бұрышының синусының көбейтінділеріне тең:

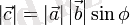
c векторы a мен b векторларының әр-қайсысына ортогональ
c векторы abc үштігі оң болатындай бағытталған.
Белгілеулер:

Геометриялық мағынасы бойынша 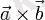векторлық көбейтіндісі 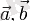векторларына керілген бағатталған параллелограммның ауданы болып табылады.

Аралас көбейтінді
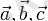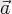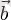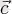векторларының аралас көбейтіндісі деп векторын және векторларының векторлық көбейтіндісіне скаляр көбейткенге тең скалярды айтады:

(теңдікте скаляр және векторлық көбейтінділер белгілері пайдаланылған).
Кейде аралас көбейтіндіні векторлардың үштік скаляр көбейтінді деп те атайды, нәтижесі скаляр болғандықтан болу керек (дәлірек айтқанда -- псевдоскаляр болады).
Геометриялық түрде аралас көбейтіндісі 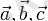векторларына керілген (бағатталған) параллелепипед көлемі болып табылады.

3.Векторлық кеңістік.

Бос емес элементтері еркін векторлар деп аталатын V=∅ жиынының элементтері үшін қосу және векторды скалярға көбейту амалдары анықталып және мынадай шарттар:

a+b=b+a, a+b+c=a+b+c, a+∅=a, a+-a=∅, 1-a=a, αμa=αμa, α+μa=αa+μa, αa+b=αa+αb

орындалса V жиынын сызықты векторлық кеңістік, ал төменде көрсетілген сегіз шарт оның аксиомалары деп аталады.
Векторлық кеңістіктің аксиомалары
1)a+b=b+a;
2)(a+b)+c=a+(b+c);
3);
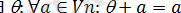4)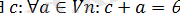, c=-a;
5);
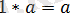6);
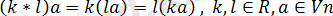7);
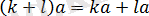8);
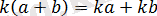Анықтама. a1, a2,..., ak векторлары немесе векторлар жүйесі берілсін
l1, l2, ..., ln 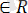сандар l1* a1+ l2* a2+...+ ln* an=b, онда b векторы a1, a2,..., ak векторының сызықтық комбинациясы деп аталады.
Анықтама.a1, a2,..., ak векторлар жүйесі сызықтық тәуелді деп аталады, егер олардың нөлдік сызықтық комбинациясында (сызықтық комбинация нолге тең) ең болмаса бір коэффициент нолден өзгеше болса.

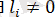
Анықтама. a1, a2,..., ak векторлар жүйесі сызықтық тәуелcіз деп аталады, егер олардың нөлдік сызықтық комбинациясында (сызықтық комбинация нолге тең) барлық коэффициент нолге тең болса.
Сызықты тәуелділіктің қасиеттері:
Егер векторлар жүйесінде a1, a2,..., akең болмаса бір вектор нолдік болса, онда бұл жүйе сызықты тәуелді болады.
Егер векторлар жүйесінде a1, a2,..., akекі тең вектор бар болса, онда бұл жүйе сызықты тәуелді болады.
Егер сызықты тәуелді жүйеге бірнеше вектор қоссақ, онда жаңа жүйе сызықты тәуелді болады.
Егер сызықты тәуелсіз жүйеден бірнеше вектор алсақ, онда жаңа жүйе тәуелсіз болады.
a1, a2,..., akсызықты тәуелді болуы үшін, оның ең болмаса бір векторы қалғандары арқылы өрнектелуі қажетті және жеткілікті.

4.Вектордың берілген базиске қарағанда координаттары және олардың қасиеттері

Ұзындықтары тең және бағыттары бірдей бағытталған кесінділер жиыны векторлық кеңістік болады: V={a, b,..., x} V векторлық кеңістіктің реттелген e1, e2,..., en векторлар жүйесінің векторлары сызықты тәуелсіз және кез келген а∈V векторы осы жүйенің векторлары арқылы жіктелсе (сызықтық комбинация), онда e1, e2,..., en векторлар жүйесін V векторлық кеңістіктің базисі, ал e1, e2,..., en базистік векторлар деп аталады. Анықтама бойынша векторлар жүйесі базис болу үшін:
a1∈R, i=1,..., n сандары табылып a1e1+a2e2+...+anen теңдігі тек a1=...=an=0 болғанда ғана орындалуы керек.
a=∅ болса a=a1e1+a2e2+...+anen теңдігі орындалатып, мұндағы а1, а2,..., аn∈R сандарының бәрі бірдей нөлге тең емес болуы қажет.
Базистік векторларының саны V векторлық кеңістіктің өлшемі деп аталады және dim(V)=n деп белгіленеді (dimension-өлшем). Енді V векторлық кеңістіктің өлшемін табуды қарастырайық.
Компланар емес e1=OA, e2=OB, e3=OC векторлары үшін xe1+ye2+ze3=∅ теңдігі тек қана x=y=z=∅ болғанда орындалады және кез келген a векторы 4⁰ қасиеті бойынша e1, e2,e3 векторлары арқылы сызықты өрнектеледі:
a=xe1+ye2+ze3, (1)
мұндағы x, y, z сандарының ең болмағанда біреуі нөлге тең емес. Демек, В=(e1, e2,e3) векторлар жүйесі V векторлық кеңістіктің базисі болады және тәуелсіз векторлар саны үшке тең, сондықтан dim(V)=3. Мұндағы кеңістікті үш өлшемді векторлық кеңістік деп атайды және V3 деп белгілейді. В=(e1, e2,e3) кеңістіктің базисі. Мұнда e1 векторы бірінші, e2 екінші, e3 үшінші базистік векторлар деп талады.
Ескерте кететін жай e1, e2,e3, e2,e3, e1, (e3, e2, e1) әртүрлі базистер.
формуланы векторды базистік векторларға жіктеу формуласы деп атайды. Мұндай жіктелу тек қана біреу болатын, яғни e1, e2,e3 векторларына сәйкес x, y, z сандарының тек қана бір үштігі бар болады. Шынында да, егер мұндай жіктелу екеу деп жорысақ, тағы да бір реттелген x1, y1, z1∈R сандары сандар үштігі табылып:
a=x1e1+y2e2+z1e3 (2)
Онда (1), (2) теңдіктерінен ∅=x-x1e1+y-y1e2+(z-z1)e3 теңдігін табамыз. Ал, e1, e2,e3 тәуелсіз векторлар жүйесі болғандықтан, мұндай теңдік тек x-x1=∅, y-y1=∅, (z-z1)=∅ немесе x=x1,y=y1,z=z1 болғанда дұрыс. Олай болса а векторы үшін (1) жіктелуден басқа жіктелуі жоқ. (1) формуладағы x, y, z сандары а векторының В(e1, e2,e3) базисіне қатысты координаттары немесе компоненттері деп аталады және оны былай жазып көрсетеді a(x, y, z), мұндағы х бірінші, у екінші, z үшінші координаттары. Базистік векторлардың координаттары e1 1, 0, 0, e20, 1, 0, e30, 0, 1 болады.Вектордың берілген базиске қатысты координаттарының қасиеттерін қарастырайық:
Векторлардың қосындысының координаттары қосылғыштардың координаттарының қосындысына тең болады.
Дәлелдеу: a∈ V3 және b∈ V3 векторларын базистік векторлар бойынша жіктеп жазайық: a=x1e1+y1e2+z1e3, b=x2e1+y2e2+z2e3 сондықтан

a+b=x1+x2e1+y1+y2e2+(z1+z2)e3

Векторды скалярға көбейткенде берілген вектордың әрбір координатасы сол скалярға көбейтіледі.
Дәлелдеу:
αa=αxe1+ye2+ze3, α∈R
αa=αxe1+αye2+(αz)e3

{e1, e2,e3} базисінде координаттарымен берілген a(a1, a2, a3) және b(b1, b2, b3) векторлары коллинеар болуы үшін олардың координаттары пропорционал болуы қажетті және жеткілікті.
Дәлелдеу: a∥b⇒b=αa⇒b1e1+b2e2+b3e3=αa1e1+αa2e2 +αa3e3⇒b1=αa1, b2=αa2, b3=αa3⇒b1a1=α,b2a2=α,b3a3=α.
Демек a және b векторларының координаттары пропорционал. Керісінше, a және b векторларының координаттары пропорционал болсын. b1a1=b2a2=b3a3=α. Бұл теңдіктердің біріншісін е1, екіншісін е2, үшіншісін е3 көбейтіп қоссақ b=αa. Бұдан a және b векторлары коллинеар болатындығы шығады.

5.Екі бірдей соңғы өлшем бірлігінің кез келген екі векторлық кеңістігінің арасындағы изоморфизм туралы теорема

Теорема 2. Екі соңғы өлшемді векторлық кеңістіктер өзара изоморфты болуы үшін олардың өлшем бірлігі бірдей болуы қажетті және жеткілікті.
Дәлелдеу. Өзара изоморфты екі кеңістіктің біреуінде n векторларынан тұратын сызықтық тәуелсіз жүйе болып, векторлардың көп мөлшерінен тұратын сызықтық тәуелсіз жүйе болмаса, онда ол екінші векторлық кеңістік үшін де әділетті болады.
Басқаша айтқанда: өзара изоморфты кеңістік бір өлшем бірлігіне ие.
Шарт жеткілікті. Оған көз жеткізу үшін кез келген n-мөлшерлі U кеңістігі n-мөлшерлі Аn арифметикалық кеңістігіне изоморфты екендігін дәлелдейік. u1, u2, ..., un - U кеңістігінің туынды базисі болсын. Онда әрбір uϵU векторы міндетті түрде былай жазылады:
u=x1u1+x2u2+...+xnun

u=x1u1+x2u2+...+xnun∈U векторына сәйкес v={x1, x2, ..., xn}∈An векторын қоя отырып, U және An кеңістіктері арасындағы ізделініп отырған изоморфты сәйкестікке қол жеткіземіз (дәлелдеу u∈U, u'∈U екі векторын қосқан кезде олардың сәйкес координаталары қосылатындығынан, ал u∈U векторын қандай да бір λ санына көбейткен кезде дәл сол λ санына u векторының координаталары да көбейтілетіндігінен шығады).
Ескерту 1.

u1=1∙u1+0∙u2+...+0∙un,u2=0∙u1+1∙u2+ ...+0∙un, ... ... ... ... ... ... .. ... ... ... ... ...un=0∙u1+0∙u2+... +1∙un,

болғандықтан, U және An векторлық кеңістіктері арасындағы изоморфизм анықталған жағдайда U кеңістігінің u1, u2, ..., un базисі An кеңістігінің векторлар жүйесіне өтеді

v1=1, 0,..., 0,v2=0, 1,..., 0, ... ... ... ... ... .vn={0, 0,..., 1}

және векторлардың осы жүйесі An кеңістінің базисін құрайды.
Жалпы U және V - екі изоморфты векторлық кеңістіктер. U және V кеңістіктерінің арасындағы u--v изоморфтық сәйкестік кезінде (ерікті түрде таңдалған) U кеңістігінің кез келген u1, u2, ..., un базисіне V кеңістігінің v1, v2, ..., vn қандай да бір базисі сәйкес келеді және U кеңістігінің u=x1u1+x2u2+...+xnun кез келген векторына u векторы u1, u2, ..., un базисіне қатысты координаталары тәрізді v1, v2, ..., vn базисіне қатысты координаталары бар V кеңістігінің v=x1v1+x2v2+...+xnvnвекторына сәйкес келеді. Керісінше, u1, u2, ..., un және v1, v2, ..., vn туынды базистері бойынша n-мөлшерлі екі кеңістіктің арасынан таңдай отырып және осы базистерге қатысты х1, x2, ..., xn бірдей координаталарға ие u=x1u1+x2u2+...+xnun∈U және v=x1v1+x2v2+...+xnvn∈V кез келген екі векторды салыстыра отырып, U және V кеңістіктері арасындағы изоморфизмге u--v қол жеткіземіз.
Ескерту 2. Болашақта біз n аталған мөлшерінің векторлық кеңістіктерін Vn, Un, Ln арқылы белгілейтін боламыз, сондай-ақ олардың арифметикалық n-мөлшерлі кеңістігі үшін (олардың барлығы изоморфты) An белгілемесін сақтаймыз.

6.Векторлық кеңістіктің ішкі кеңістігі. Векторлардың сызықтық тәуелділігі және векторлық кеңістік базисі туралы ары қарайғы теоремалар

1. Векторлық кеңістіктің ішкі кеңістігі анықтамасы. V векторлық кеңістікте келесі шарттарды қанағаттандыратын L векторлар жиынтығы болсын:
10 L құрамындағы u1 және u2 қандай болғанына қарамастан, олардың жалпы сомасы да L жиынтығына тиесілі болады.
20 L құрамындағы u векторы мен λ саны қандай болғанына ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.