Қос интегралды есептеу

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 22 бет
Таңдаулыға:

Қос интегралдың қолданылулары
Мазмұны
Кіріспе
Қос интеграл
Квадратталатын фигуралар және ауданның анықтамасы
Қос интеграл анықтамасы
Қос интегралдың геометриялық мағынасы
Қос интегралдың қасиеттері
Қос интегралда айнымалыларды алмастыру
Қос интегралды есептеу
Қос интегралдың (геометриялық) қолданулары
Жазық фигураның ауданын есептеу
Дененің көлемін есептеу
Бет ауданын есептеу
Қос интегралды физика және механика есептеріне қолдану
Пластинканың массасы
Пластинканың ауырлық центірінің координаттары
Пластинканың инерция моменттері
Пластинканың статикалық моменттері
Қос интегралдың қолданылуларына қатысты есептер
Қос интегралдардың геометриядағы есептеулері
Қос интегралдың физика және механикадағы есептеулері
Қорытынды
Пайдаланған әдебиеттер

Кіріспе

Интеграл(лат. іnteger - бүтін) - математиканың маңызды ұғымдарының бірі. Интеграл ұғымы бір жағынан - туындысы бойынша функцияны іздеу (мысалы, қозғалған нүктенің жүріп өткен жолын өрнектейтін функцияны сол нүктенің жылдамдығы бойынша табу), екінші жағынан - аудан, көлем және доға ұзындығын өлшеу, күштің белгілі бір уақыт ішінде атқарған жұмысын табу, т.б. қажеттіліктерден пайда болып еді. Осыған қатысты интеграл анықталмаған интеграл және анықталған интеграл болып ажыратылады. Міне, осыларды есептеу интегралдық есептеудің міндеті болып саналады. Интеграл сөзін алғаш рет (1690) швейцариялық ғалым Якоб Бернулли қолданған;өзінің шексіз аз бөліктерінің қосындысы түрінде қарастырылатын бүтін шама.
Интеграл ұғымы көп айнымалысы бар функцияларға да қолданылады. Интегралдық есептеудің аудан мен көлемді табуға байланысты бірқатар есептерін ежелгі грек математиктері шешкен. IX - XV-ғасырларда Орта және Таяу Шығыс ғалымдары Архимед еңбектерін араб тіліне аударып, ежелгі математиканың табыстарын кейінгі ұрпақтарға жеткізді. Әйткенмен, оларды одан әрі дамыта алмады. Тек XVI - XVII-ғасырларда ғана табиғаттану ғылымдарының жетістіктері интегралдық есептеудің одан әрі дамуын қажет етті. Интегралдық есептеудің негізгі ұғымдары мен идеялық жүйесін бір-біріне тәуелсіз түрде Исаак Ньютон мен Готфрид Лейбниц жасады. Интегралдық есептеу термині мен интеграл таңбасы Лейбництен бастап қолданылып келеді. Интегралдық есептеудің әрі қарай дамуы швейцариялық математик Иоганн Бернуллидің, әсіресе, Леонард Эйлердің есімдерімен тығыз байланысты. XIX-ғасырдың басында француз математигі Огюстен Луи Коши шектер теориясы негізінде интегралдық есептеу мен дифференциалдық есептеуді қайта құрды. Интегралдық есепті дамытуға XIX-ғасырда орыс ғалымдары Михаил Остроградский, Виктор Буняковский және Пафтуний Чебышев үлкен үлес қосты. Жалпы екі еселік интеграл дененің көлемін есептеу және пайдалану жолдар, физикалық және механикалық қоланулар қарастырылады. Сондықтан да, қос интеграл ұғымына қысқаша тоқталып, қолданулары мен мақсаттарын толық түсіндіруге тырысамыз.
Курстық жұмыстың мақсаты:
Қос интеграл ұғымын түсіндіре отырып, қос интегралдың қолдануларына толық тоқталу. Қарапайым өмірде қос интегралдың қажеттілігін айқындау;
Курстық жұмыстың міндеттері:
Қос интеграл ұғымына қысқаша тоқталым;
Қос интегралдың қолдануларын ашып көрсету;
Қос интегралдың қолданылуларына арналған есептерді ұсыну;

Қос интеграл
Квадратталатын фигуралар және ауданның анықтамасы
Бұл ұғым жазықтықта жатқан көп фигураның ауданы туралы ұғым.
Біз қос интеграл ұғымы мен қолдануларын толыққанды түсіндіре алу үшін ең алдымен квадратталған фигуралар мен ауданының анықтамасын қарастырып кетуді жөн санадық.
Көп бұрышты ұғым деп саны шектелген көпбұрыштардан құралған жиынды түсінеміз.

Көпбұрышты фигураның ауданы теріс емес санмен өрнектеледі.
Көп бұрышты фигураның мынадай қасиеттері бар:
1.Бір сарындылық. Егер көп бұрышты P фигура Q фигурасының ішінде жатса,

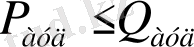
2.Аддитивтік. Егер көп бұрышты фигуралар 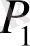мен 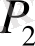-ның ортақ ішкі нүктелері жоқ болып, ал көпбұрышты фигура 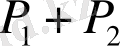сол фигуралардың біріктірмесі болса,

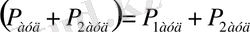
3.Инварианттық. Егер көп бұрышты фигуралар 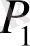мен 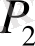өзара конгурентті болса,

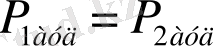
Көпбұрышты фигураның ауданы туралы төмендегіні айтуға болады. Жоғары үш қасиет сақталатын жазықтықтағы кейбір F фигурасына қолдану төмендегісінше іске асырылады.
Қарастырылатын F фигурасының ішіне бүтіндей жататын барлық мүмкін көпбұрышты P фигураларды тұрғызамыз да, оларды қамтылған P көпбұрышты фигуралар деп атаймыз.
Қамтылған фигуралардың аудандары жоғарыдан шектелгендіктен, дәл жоғары шекара

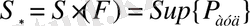
P Euro F
бар болады.
Сонан кейін фигура F бүтіндей ішінде жататын барлық мүмкін көпбұрышты Q фигуралар тұрғызамыз да, оларды қорғаушы (қамтушы) көпбұрышты фигуралар деп атаймыз.
Қамтушы фигуралардың аудандары төменнен шектелгендіктен, дәл төменгі шекара

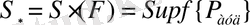
Q F
бар болады.
Әрбір қамтылған көпбұрышты фигураның ауданы кез келген қамтушы көпбұрышты фигураның ауданынан артық еместігін ескерсек,

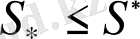
арақатынасы орындалады.
Егер қамтылған және қамтушы фигуралардың аудандары үшін

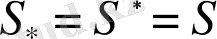
ендігі орындалса, F-квадратталатын фигура, ал S саны сол F фигурасының ауданы деп аталады.

Қос интеграл анықтамасы
Осы курстың бірінші бөлімінде біреселі интегралды қарастырып, онда физика, механика есептерін шығардық. Осы сияқты екі,үш, т.с.с еселі интегралдардың көмегімен физика, механика есептерін шығаруға болады, мысалы, дененің массасын, атқарылған жұмысты, кез келген беттің ауданын, дене көлемін, пластиналардың механикалық параметірлерін т.с.с. Оларды есептеуге қажетті қос интегралды қарастыратын боламыз.
Қос интеграл анықталған интегралдың интегралдың екі айнымалыға тәуелді функция жағдайының
жалпыламасы болып табылады. XOY жазықтығының тұйық D облысында z=f(x,y) үзіліссіз функциясы берілсін.
D облысын саны n-ге тең элементар Di(i=1,2,...,n)бөліктеріне бөлшектеп, олардың аудандарын ∆Si, ал диаметрлерін (облыс нүктелері арасындағы ең үлкен қашықтықты) di деп белгілейміз. (1.1-сурет).
у

Di
Di

О Х
1.1-сурет

Әрбір Di облысында кез келген Mi(xi,yi) нүктесін алып, сол нүктедегі f(xi,yi) түріндегі функция мәнін ∆Si-ге көбейтіп, барлық осындай көбейтінділерден

fx1,y1∆S1+fx2,y2∆S2+...+fxn,yn∆Sn=i =1nfxi,yi∆Si (1.2.1)

қосындысын тұрғызымыз. Мұндай қосынды D облысындағы z=f(x,y) функциясының интегралдық қосындысы деп аталады. n--infinity,maxdi--0 шартында (5.1) интегралдық қосындысының шегін қарастырайық. Егер осы шек бар болып және ол не D облысының бөлшектену тәсіліне, не ондағы нүктелердің қалай алынатынына тәуелсіз болса, онда ол D облысы бойынша f(x,y) функциясынан алынға қос интеграл деп аталады және

Dfx,ydxdy немесе Dfx,ydS

деп белгіленеді. Сонымен, қос интеграл

Dfx,ydxdy=limï--infinity,maxdi--0 i=1nf(xi,yi)∙∆Si (1.2.2)

Теңдігімен анықталады. Мұндайда f(x,y) функциясы D облысында интегралданатын функция, D - интегралдау облысы, x және y- интегралдау айырмалары, dxdy (немесе dS)- аудан элементі деп аталады.
Қандай да f(x,y) функциясының қос интегралы бола бере ме? Бұл сұраққа дәлелдеусіз келтіретін төмендегі теорема жауап береді.
Теорема 1.2.1. (фунция интегралдануының жеткілікті шарты). Егер f(x,y) функциясы тұйық D облысында үзіліссіз болса, онда ол осы облыста интегралданады.
Қос интегралдың геометриялық мағынасы
Қос интеграл геометриялық тұрғыда дене көлемін кескіндейді. Расында 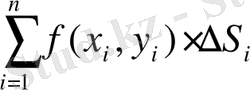қосындысындағы жекелеген 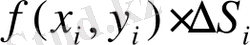көбейтіндісі i-ші цилиндр көлеміне тең. Мұндай цилиндрлердің табанында жатқан 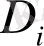бөлігінің ауданы 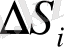болса, биіктігі 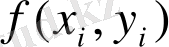-ге тең, цилиндрлердің өздері үстінен 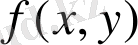бетімен, астынан 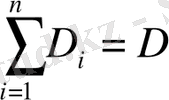облысымен, жан-жағынан Oz осіне параллель жасаушыларымен шектелген,

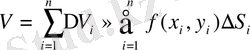
болғандықтан шегінеді.

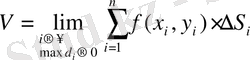
немесе (1.2.2) теңдігіне сәйкес

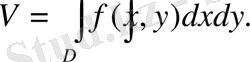
Сонымен, теріс емес 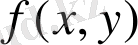функциясынан алынған қос интеграл шамасы цилиндірлік беттің көлеміне тең, мұндағы 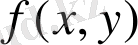- денені жоғарыдан шектейтін бет теңдеуі. Қос интегралдың геометриялық мағынасы осындай.

Қос интегралдардың қасиеттері
Бір еселі анықталған интегралға орындалатын қасиеттер екі еселі интегралға да орындалады. Біз олардың тұжырымдарын келтірейік.
1-қасиет. Егер f(x;y), ϕ(x;y) функциялары D облста интегралданса және с1,с 2 - const, онда с1 f(x;y)+-с2ϕ(x;y) функциясында D облыста интегралданады және
с1 f(x;y)+-с2ϕ(x;y)dxdy = c1 f(x;y)dxdy+-с2ϕ(x;y)dxdy
Теңдік орындалады.
2-қасиет. Егер f(x;y) пен ϕ(x;y) функциялары D облыста интегралданса,онда f(x;y) · ϕ(x;y) функция да осы облыста интегралданады.
3-қасиет. Егер f(x;y) функция D
облыста интегралданса және ауданы
нөлге тең Г қисық сызығы осы R
облысты ортақ ішкі нүктесі жоқ D1 мен
D2 байланысты облыстарға бөлсе, онда D1 D2
функция D1 мен D2 облыстарда
интегралданады (10.4-сурет) және:

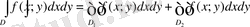
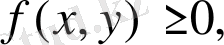
4-қасиет. Егер 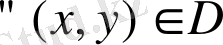болса, онда

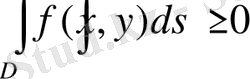
5-қасиет. Егер f(x;y) және ϕ(x;y) функциялар D облыста интегралданса және облыстың барлық 10.4-сурет
нүктелерінде f(x;y) = ϕ(x;y) теңсіздігі орындалса,
онда
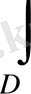f(x;y)dxdy 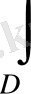=ϕ(x;y)dxdy
теңсіздік орындалады.
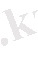
6-қасиет. Егер f(x;y) функциясы D облыста интегралданса, онда 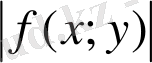функциясында осы облыста интегралданады және

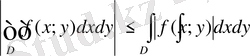
7-қасиет. 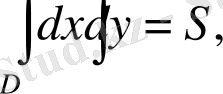себебі 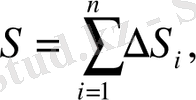мұндағы S - аймақтың ауданы.
8-қасиет. Функцияның орта мәні туралы теорема.
(D) облысы шектелген, ал f(x,y) функциясы осы облыста үздіксіз болсын. Онда (D) облысында міндетті түрде бір 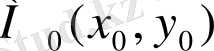нүктесі табылып

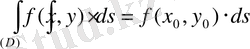
теңдігі орындалатын болады.
9-қасиет. (орта мән туралы теорема). Егер f(x;y) пен ϕ(x;y) функциялары D облыста интегралданса, ϕ(x;y) функциясы осы облыста теріс (оң ) емес болса, М мен m сандары f(x;y) функциясының D облысындағы сәйкес ең жоғарғы, ең төменгі шекарасыֿ бар болса, онда m = μ = M теңсіздігін қанағаттандыратын μ саны табылып,
f(x;y) ϕ(x;y)dxdy= μϕ(x;y)dxdy
теңдігі орындалады.
Осы қасиеттен: егер f(x;y) функция байланысты D облыста үзіліссіз болса, онда осы облыста А(͞x,͞y) нүкте табылып. u=f(͞x,͞y) және
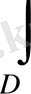f(x;y) ϕ(x;y)dxdy= f(͞x,͞y)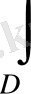ϕ(x;y)dxdy
болады.
Қос интегралда айнымалыларды алмастыру
(Жалпы жағдай. Қисық сызықты координаттар жүйесіндегі қос интеграл.)
(D) облысында f(x,y) екі айнымалының функциясынан декарт координат жүйесінде
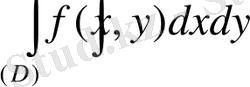(1.5.1)
қос интегралын есептеу керек болсын. Ол үшін
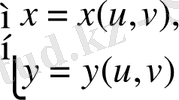(1.5.2)
(мұндағы u, v-қисық сызықты координат жүйесі) алмастыруын жасаймыз. Әрине x(u,v) және y(u,v) функциялары 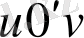жазықтығындағы 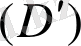облысындағы үздіксіз функциялар. Сонымен қатар (D) облысын 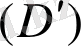облысына түрлендіргенде пайда болатын якобиан деп аталатын екінші ретті мына
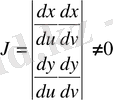(1.5.3)
анықтауыш нөлге тең емес. Бұл жағдайда 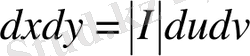(аудан элементі). Ендеше, (1.5.1) интегралы (1.5.2) алмастыруы арқылы
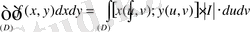(1.5.4)
түрге келетін болады.
Ескерту. Осы алмастыруды жүргізу нәтижесінде якобианның рөлі интегралдау (D) облысы екінші 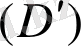облысына түрленеді де облысты созу не қысу рөлін атқарады.
Сонымен, қос интегралда жүргізілген айнымалыларды алмастыру екі мақсатта жүргізілетін болады екен:
а) қос интеграл астындағы функцияны қарапайым түрге келтіру,
б) интегралдау облысын дұрыс әрі қарапайым облысқа келтіру.
1.6. Қос интегралды есептеу
Алдымен, қос интегралды D тіктортбұрышты облыста есептейік.
1.6.1-Теорема. D={(x,y):α=x=b,c=y=d} тіктөртбүрышты облыста fx,y функциясының

J=Dfx,ydxdy (1.6.1)
қос интегралы бар болсын.
Егер кез келген x∈[a,b] үшін
Jx=cdfx,ydy (1.6.2)
анықталған бір еселі интегралы бар болса, онда қайталанған

abJxdx=abdxcdfx,ydy

Интегралы бар және мына теңдік орындалады:

Dfx,ydy=abdxcdfx,ydy. (1.6.3)
Дәлелдеу. Тікбұрышты D облысты a=x0x1x2...xn=b және c=y0y1y2 ...yn=d нүктелерімен OX,OY осьтеріне параллель түзулермен n∙m дербес төртбұрыштарға бөлейік
Dkl=xk-1=xxk∩yl-1=y=yl,

k=1.n, l=1,m, ∆xk=xk-xk-1, ∆yl=yl-yl-1,

және Dk l тіктөрбұрыштарға fx,y функциясының сәйкес ең үлкен және ең кіші шекарасы Mkl , mkl болсын. Онда барлық x,y∈Dkl үшін

mkl=f(x,y)=Mkl

Теңсіздігі орындалады. Теңсіздіктегі x=xk болсын, мұндағы xk∈xk-1,xk. Соңғы теңсіздікті айнымалы бойынша yl-1 - ден yl- ге дейін y айнымалы боцынша интегралдайық:

mklyl-1yldy=yl-1yfxk,ydy=Mklyl-1y ldy.

Осыдан:

mkl∆y1=J(xk)=Mkl∆yl,

мұндағы J(xk) интегралы бар, себебі (1.6.2) интеграл бар. Соңғы теңсіздік 1-ден m-ге дейін l бойынша қосымша алайық, сонда l=1mmkl∆yl=Jxk= =l=1mMkl∆yl.соңғы теңсіздікті - ға көбейтіп, 1-ден -ге дейін бойынша қосынды алайық, сонда

k=1n∆xkl=1mmkl∆yl=k=1nJ(xk)∆xk=k= 1mMkl∆yl. (1.6.4)

Егер Dkl дербес тіктөртбұрыштың ең үлкен диаметрі болса, әрі нөлге ұмтылса, онда Dkl дербес тіктөртбұрыштың ең үлкен ∆xk қабырғасы да нөлге ұмтылады. (1.6.4) теңсіздіктің ортасында J(x) функцияның интеграл қосындысы, ал оның оң жағы мен сол жағында қос интегралдың сәйкес төменгі мен жоғары қосындылары. Сондықтан ∆xk--0 болғанда, қос интегралдың төменгі мен жоғарғы қосындысы қос интегралға ұмтылады, онда k=1nJ(xk)∆xk интеграл қосындысының да интегралы бар және ол осы қос интегралға ұмтылады, яғни
abJxdx=abdxcdfx,ydy.

Демек, қайталанған қос интегралы бар. Теорема дәлілденді.
(1.6.5) формуланың оң жағындағы бірінші интеграл сыртқы, ал екінші интеграл ішкі интеграл деп аталады. Тіктөртбұрышты облыста қос интегралды есептегенде кез келген интегралдан бастап есептеуге болады.
Дәлелденген теораманың тұжырымында қос интегралдың және c,d сигментте тағайындалған кез келген y үшін J1y=abfx,ydx интегралының бар болуын ұйғарып, қайталанған

cdJ1ydy=cddyabfx,ydx (1.6.5)

Интегралының да бар болуын дәлелдеуге болады.
Енді кез келген қисық сызықты облыс үшін қос интегралды қайталанған интегралға келтіруге болатынын қарастырайық.
2. Бізге D={x,y:a=x=b, y1x=y=y2x} облыста анықталған fx,y фүнкция берілсін, мұндағы y1x, y2(x) функциялары [a,b] сегментте үзіліссіз болсын. Тұйық D облыста OY осіне параллел жүргізілген түзулер y1x, пен y2(x) ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.