Шектері шексіз интегралдар

Мазмұны

Кіріспе

Мен өзімнің курстық жұмысымда меншіксіз интегралдар туралы қарастырамын. Өзіндік емес интеграл немесе Меншікшіз Интеграл - Риман интегралы бар болуы үшін төмендегі екі шарттың орындалуы қажетті екені белгілі: 1) функцияның интегралдау кесіндісінде шенеулі болуы; 2) интегралдау кесіндісінің ұзындығы шенеулі болуы. Осы екі шарттың ең кемінде біреуінің орындалмауы өзіндік емес интеграл ұғымына әкеледі. Меншікшіз Интеграл - шектелмеген функциялар және шексіз аралықта берілген функцияларды интегралдау кезінде классикалық интеграл ұғымын жалпылау. Екі жағдайда да меншікшіз интеграл қосымша шектік ауысудың көмегімен әдеттегі интеграл арқылы анықталады.

• Егер [a, N] аралығының кез келген ақырғы бөліктерінде f(x) функциясы интегралданса және бар болса, онда оны [a, ∞\infty) интервалындағы f(x) функциясының меншікшіз интегралы деп атайды және түрінде белгіленеді.

- Егер бұл шек бар болса меншікшіз интеграл жинақты, ал шегі болмаса жинақсыз делінеді.

Меншікшіз интегралдың дәл анықтамасын 1823 жылы О. Коши (1789 - 1857) берген. Меншікшіз интегралды есептеуде параметрлері бойынша дифференциалдау және интегралдау, қатарларға жіктеу, қалынды теориясын қолдану, т. б. әдістер қолданылады.

Курстық жұмыстың мақсаты - шектері шексіз интеграл ұғымына түсінік беріп және практикада қоладнылуын көрсетіп, әр түрлі теоремалар арқылы түсіндіру.

Курстық жұмыстың міндеттері:

• Меншіксіз интеграл анықтамасын беріп, теоремаларды түсіндіру;
• Шектері шексіз интегралдарға түсінік беріп, олардың жинақтылық белгілерін көрсету;
• Меншіксіз интегралдардың практикада кездесетін интегралдарды есептеп шығару.

I. Функцияның шегі

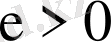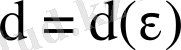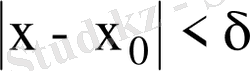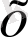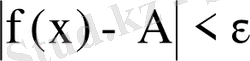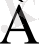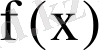Анықтама. Егер кішкене саны үшін, осы саннан тәуелді санын теңсіздігін қанағаттандыратын барлық нүктелерінде теңсіздігі орындалатындай етіп табуға болса, онда саны -тің 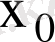нүктесіндегі шегі деп аталады да, 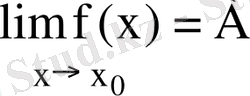деп белгілінеді. Аталған шек 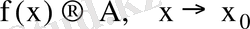түрінде де жазылады.

1 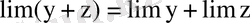. Қосындының шегі шектердің қосындысына тең.

2 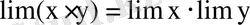. Көбейтіндінің шегі шектердің көбейтіндісіне тең.

3 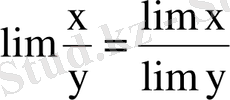, 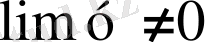. Егер 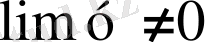болса, онда бөлшектің шегі алымының шегін бөлімнің шегіне бөлгенге тең.

4 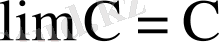. Тұрақты шаманың шегі сол шаманың өзіне тең.

5 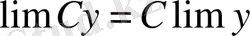. Тұрақты шаманы шектің сыртына шығаруға болады.

*Оң жақты/ сол жақты шектерді бір жақты шектер деп атайды

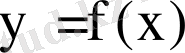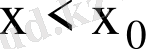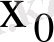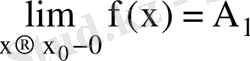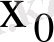функциясының болып х -тің -ге ұмтылғандағы -ге тең шегі осы функцияның сол жақты шегі деп аталады да деп белгіленеді, ал болып х -тің -ге ұмтылғандағы -ге тең шегі функцияның оң жақты шегі деп аталады да, 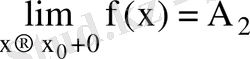деп белгіленеді.

II. Анықталмаған интеграл

1-Анықтама. Егер кез келген х бір F(х) табылып F'(х) = f(x) тең болып, F(х) -ті берілген аралықта f(x) үшін оның алғашқы функциясы деп айтады.

2-Анықтама. Барлық алғашқы функцияның жиынтығын F(х) +С, f(x) функция анықталмаған интеграл дейді.

Төмендегі символмен белгіленеді:

$$\int_{}^{}{\mathbf{f}\left( \mathbf{x} \right) \mathbf{dx = F(x) + C}}$$

$$\int_{}^{}\mathbf{- \ интегралдың\ белгісі}$$

f(x) - интеграл астындағы функция

$$\mathbf{f}\left( \mathbf{x} \right) \mathbf{dx - инт. \ астн. \ өрнек}$$

Қасиеттері:

1) ʃ d F(x) =F(x) +C

2) d(ʃ f(x) dx) =f(x) dx

3) ʃ k f(x) dx=kʃ f(x) dx

4) ʃ (f(x) ±g(x) ) dx=ʃ f(x) ±ʃ g(x) dx

Негізгі кестесі:

1) $\int_{}^{}{dx = x + C}$

2) $\int_{}^{}{x^{n}dx = \frac{x^{n + 1}}{n + 1}} + C, \ \ (n \neq - 1)$

3) $\int_{}^{}\frac{dx}{x} = \lnx + C$

4) $\int_{}^{}{a^{x}dx = \frac{a^{x}}{lna}} + C$ → $\int_{}^{}{e^{x}dx} = e^{x} + C$

5) $\int_{}^{}{sinxdx = - cosx + C}$

6) $\int_{}^{}{cosxdx = sinx + C}$

7) $\int_{}^{}{\frac{dx}{\cos^{2}x} = tgx + C}$

8) $\int_{}^{}\frac{dx}{\sin^{2}x} = - ctgx + C$

9) $\int_{}^{}{\frac{dx}{\sqrt{a^{2} - x^{2}}} = \arcsin\frac{x}{a} + C}$ → Дербес түрі $\int_{}^{}{\frac{dx}{\sqrt{1 - x^{2}}} = arcsinx + C}$

10) $\int_{}^{}{\frac{dx}{x^{2} + a^{2}} = \frac{1}{a}arctg\frac{x}{a} + C}$ → $\int_{}^{}\frac{dx}{1{+ x}^{2}} = arctgx + C$

11) $\int_{}^{}{\frac{dx}{x^{2} - a^{2}} = \frac{1}{2a}\ln\left \frac{x - a}{x + a} \right + C}$ → $\int_{}^{}{\frac{dx}{x^{2} - 1} = \frac{1}{2}\ln\left \frac{x - 1}{x + 1} \right + C}$

12) $\int_{}^{}\frac{dx}{\sqrt{x^{2} \pm a}} = \ln\left x + \sqrt{x^{2} \pm a} \right + C$

3-Анықтама. Анықталмаған интегралдың негізгі кестесін және оның қасиеттерін қолданатын әдісті тікелей интегралдау әдісі деп айтады.

III. Анықталған интеграл

Қисықсызықты трапецияның ауданы туралы есеп:

1. a=x ₀ $<$ x ₁ $<$ x ₂ …. x _i ˂x _i+1 ˂ … $<$ x _n-1 $<$ ˂x _n =b

2. ξ _i Є[x _i ; x _i+1 ]

3. f(ξ _i )

4. $\delta ᵢ = \sum_{i = 0}^{n - 1}{f(ᶓᵢ) \mathrm{\Delta}}x$ ; (1) -сигма интегралдық қосынды

S $\delta = \sum_{i = 0}^{n - 1}{f(ᶓ) ox}$

ρ = $\sum_{i = 0}^{n - 1}{mᵢ\mathrm{\Delta}xᵢ}$

Р= $\sum_{i = 0}^{n - 1}{Mᵢ\mathrm{\Delta}xᵢ}$

$\lim_{x \rightarrow 0}\rho = \lim_{x \rightarrow 0}{P = P}$

$\lambda = \max\mathrm{\Delta}xᵢ$ P-қисықсызықты трапецияның ауданы

Егер интегралдық қосынды $\delta ᵢ\underset{x \rightarrow 0}{\lbrack lim}{\delta ᵢ} = ($ 2) ] болса, онда ол санды а-дан в-ға дейінгі алынған x→0 f(x) функциясының анықталған интеграл деп атайды.

Және төмендегі символмен белгілейді.

$У = \int_{a}^{b}{f(x) dx}$ a-төменгі шек, b-жоғарғы шек

Қисықсызықты трапецияның ауданы: S $= \int_{a}^{b}{f(x) dx}$

Қасиеттері:

1. $\int_{a}^{b}\begin{array}{r} f(x) dx \\ a < b \end{array} = - \int_{b}^{a}{f(x) dx}$ x _i±1 -x _i =∆x _i

a) ∆xᵢ $\gg 0$

b) xᵢ - x _i+1 ≤0 xᵢ $\leq 0$

2. $\int_{a}^{b}{f(x) dx = \int_{a}^{c}{f(x) dx + \int_{c}^{b}{f(x) dx}}}$ c $\ \in \lbrack a, b\rbrack$

3. $\int_{a}^{b}{k\ f(x) dx = k\ \int_{a}^{b}{f(x) dx}}$ (k=const) ^a

4. $\int_{a}^{b}{\lbrack f(x) \pm g(x}$ ) ] dx= $\int_{a}^{b}{f(x) dx \pm \int_{a}^{b}{g(x) dx}}$

5. f(x) $\leq g(x)$ [a, b], $\int_{a}^{b}{f(x) dx} \leq \int_{a}^{b}{g(x) dx}$

6. $\left \int_{a}^{b}{f(x) dx} \right \leq \int_{a}^{b}\left f(x) \rightdx$

7. m, M [a; b] f(x)

m(b-a) $\leq \int_{a}^{b}{f(x) dx \leq M(b - a) }$

$$\int_{\mathbf{a}}^{\mathbf{b}}\mathbf{dx = x⃒}\frac{\mathbf{b}}{\mathbf{a}}\mathbf{= b - a}$$

Ньютон-Лейбниц формуласы

$\int_{\mathbf{a}}^{\mathbf{b}}{\mathbf{f}\left( \mathbf{x} \right) \mathbf{dx = F}\left( \mathbf{x} \right) \mathbf{⃒}\frac{\mathbf{b}}{\mathbf{a}}\mathbf{=}}$ F(b) - F(a)

F’(x) =f(x) F(c) +C= $\int_{}^{}\mathbf{fdx}$

Дәлелдеуі:

Ф(x) = $\int_{a}^{x}{f(t) dt}$ Ф(x) =F(x) +C

Ф’(x) =F’(x) =f(x) Ф’(x) =f(x)

x = a $\mathbf{Ф}\left( \mathbf{a} \right) \mathbf{=}\int_{\mathbf{a}}^{\mathbf{a}}{\mathbf{f}\left( \mathbf{t} \right) \mathbf{dt = 0}}$

0=F(a) +C C= - F(a)

Ф(x) = $\int_{a}^{x}{f(t) dt = F(x) - F(a) }$

x= b $\int_{\mathbf{a}}^{\mathbf{b}}{\mathbf{f}\left( \mathbf{x} \right) \mathbf{dx = F}\left( \mathbf{b} \right) \mathbf{- F(a) }}$

Мысалы:

$\int_{- 1}^{1}\frac{dx}{1 + x^{2}} = arctg⃒\frac{1}{- 1} = arctg1 - arctg( - 1) = \frac{\pi}{4} + \frac{\pi}{4} = \frac{\pi}{2}$

IV. Меншіксіз интеграл

1. Шектері шексіз интегралдар

Біздің осы уақытқа дейін қарастырған интегралдарымыздың интегралдау аралығы шексіз болсын. Міне, осы жағдайды қарайық.

Айталық, функция f(x), (a , ∞ ) аралығында анықталған және интегралданатын болсын. Сонымен, келесі интегралды

$$I = \ \int_{a}^{l}{f(x) dx\ (l > a) }$$

қараймыз.

Егер, l- шексіз өсумен бірге, осы қарастырып отырған интеграл бір тиянақты шекке ұмтылса, онда f(x) функциясын a - дан ∞ - ке дейін интегралданатын функция деп атайды. Сөйтіп, анықтауымыз бойынша

$\int_{a}^{\infty}{f(x) dx = \ \lim_{l \rightarrow \infty}{\int_{a}^{l}{f(x) dx}}}$ (1)

Егер (1) теңдіктің оң жағында тұрған шек бар болатын болса, онда мына интегралды

$\int_{a}^{\infty}{f(x) dx. }$

жинақты интеграл деп атайды.

Егер l шексіздікке ұмтылғанда интеграл l ешбір тиянақты шекке ұмтылмаса немесе абсолют шамасы бойынша шексіз өссе, онда мына интегралдың $$ $$\int_{a}^{\infty}{f(x) dx}$$

мағынасы болмайды және бұл жағдайда интегралды жинақсыз интеграл деп аталады.

Мына төмендегі интегралдар да $$ $$\int_{- \infty}^{b}{f(x) dx}\ \ және\ \int_{- \infty}^{\infty}{f(x) dx}$$

жоғарыдағыша анықталады. Бұл екі интегралдың кейінгісін былай анықтауға да болады: $$ $$\lim_{\begin{array}{r} l_{1} \rightarrow \infty \\ l_{2} + \infty \end{array}}{\int_{l_{1}}^{l_{2}}{f(x) dx = \ \ \int_{- \infty}^{\infty}{f(x) dx}}. }$$

Алғашқы F(x ) функциясы бар, f(x) функциясы үшін интеграл $$ $$\int_{a}^{\infty}{f(x) dx}$$

кәдімгі анықталған интеграл қалай есептелініп шығарылса, ол да солай шығарылады, яғни

$\int_{a}^{\infty}{f(x) dx = F(x) \begin{matrix} \infty \\ \\ a \end{matrix} = F(\infty) - F(a) },$ (2)

мұнда

$$F(\infty) = \ \lim_{l \rightarrow \infty}{F(l) . }$$

Шынында, анықтама бойынша

$$\int_{a}^{\infty}{f(x) dx = \ \lim_{l \rightarrow \infty}{\int_{a}^{l}{f(x) dx = \lim_{l \rightarrow \infty}{\left\lbrack F(l) - F(a) \right\rbrack = \lim_{l \rightarrow \infty}{F(l) - F(a) = F(x) \begin{matrix} \infty \\ \\ a \end{matrix}.$$

1. Мысал. ∫0∞dx1+x2=arctgx∞a=π2. \int_{0}^{\infty}{\frac{dx}{{1 + x}^{2}} = arctg\ x\begin{matrix} \infty \\ \\ a \end{matrix} = \ \frac{\pi}{2}. }
2. Мысал. ∫1∞dxx2=1\ \ \int_{1}^{\infty}{\frac{dx}{x^{2}} = 1}
3. Мысал. ∫1∞1x1+1x4dx. \ \int_{1}^{\infty}{\frac{1}{x}\sqrt{1 + \frac{1}{x^{4}}}dx. }

$\lim\int_{1}^{\infty}{\frac{1}{x}\sqrt{1 + \frac{1}{x^{4}}}dx \geq \lim{\int_{1}^{l}\frac{dx}{x} = \lim_{l \rightarrow \infty}{lnl = \infty}}}$

Сөйтіп, интерграл

$\int_{1}^{\infty}{\frac{1}{x}\sqrt{1 + \frac{1}{x^{4}}}dx}$

жинақсыз.

Шексіз аралықта анықталған немесе шекті аралықтың кейбір нүктелерінде берілген функция шексіздікке айналатын интегралдар меншіксіз интегралдар деп аталады.

Егер мына интегралдар

$\int_{- \infty}^{a}{f(x) dx}\ және\ \int_{a}^{+ \infty}{f(x) dx}$

жинақты болса, онда мына интеграл да

$\int_{- \infty}^{\infty}{f(x) dx}$

жинақты болады және

$\int_{- \infty}^{\infty}{f(x) dx =}\int_{- \infty}^{a}{f(x) dx +}\int_{a}^{+ \infty}{f(x) dx}. \$ (3)

Меншіксіз интегралдардың келесі қасиеттерін айтып кетейік:

1. ∫abf(x) dx=∫b+∞f(x) dx+∫a+∞f(x) dx; \int_{a}^{b}{f(x) dx =}\int_{b}^{+ \infty}{f(x) dx +}\int_{a}^{+ \infty}{f(x) dx}; \(4)
2. егерf≥0, онда∫a+∞f(x) dx≥0; егер\ f \geq 0, \ \ \ \ \ \ \ онда\ \int_{a}^{+ \infty}{f(x) dx \geq 0; }\ \
3. ∫a+∞[f(x) ±g(x) ] dx=∫a∞f(x) dx±∫a∞g(x) dx. \int_{a}^{+ \infty}{\lbrack f(x) \pm g(x) \rbrack dx =}\int_{a}^{\infty}{f(x) dx \pm}\int_{a}^{\infty}{g(x) dx}. \
4. Егер∫a∞f(x) dx\int_{a}^{\infty}{f(x) dx}\болатын болса, онда

$\lim_{l \rightarrow \infty}{\int_{l}^{\infty}{f(x) dx = 0}}$

2. Алғашқы функцияны білмей -ақ меншіксіз интегралдардың жинақтылығы туралы біраз белгілерді келтіруге болады. Одан бұрын мен бір көмекші теоремаға тоқтап кетемін.

Лемма. Айнымалы х мына $+ \infty - \ \$ ке ұмтылғанда функция F(x) бір тиянақты шекке ұмтылу үшін p мен q сандары бір -біріне тәуелсіз шексіздікке ұмтылғанда мына F(p) - F(q) айырманың нольге ұмтылуы қажетті және жеткілікті .

Бұл лемманы екінші түрде былай тұжырымдауға болады:

Функция F(x) бір тиянақты шекке ұмтылу үшін алдын ала берілген оң мейлінше аз $\varepsilon$ санына сәйкес N саны болып табылып, осы N санынан артық p және q сандары $p, \ q\ \geq N$ үшін келесі теңсіздіктің:

$\text{}F(p) - F(q) < \varepsilon$ (5)

орындалуы қажетті және жеткілікті.

Алдымен леммадағы айтылған шарттың қажеттілігін дәлелдейік. Ол үшін аргумент x мына $+ \infty = \ -$ ке ұмтылғанда, функция F(x) тиянақты L санына ұмтылады деп ұйғарайық, яғни

$$\lim_{x \rightarrow + \infty}{F(x) = L, }$$

немесе бәрібір, алдын ала берілген оң $\varepsilon$ санына сәйкес N саны табылып, осы N - нен артық х - тер үшін келесі теңсіздік орындалады

$\left F(x) - L \right < \frac{\varepsilon}{2}$ .

Айталық, p және q мына N санынын артық кез келген сандар болсын, онда кейінгі теңсіздік бойынша:

$$\left F(p) - L \right < \frac{\varepsilon}{2},$$

$\left F(q) - L \right < \frac{\varepsilon}{2}.$ (6)

Егер айнымалы x өзінен кіші a санына ұмтылғанда функция F(x) бір тиянақты шекке ұмтылуы үшін, p мен q сандары өздерінен кіші a санына бір - біріне тәуелсіз ұмтылғанда мына $F(p) - F(q)$ айырманың нольге ұмтылуы қажетті және жеткілікті.

Енді мәселе мына функция

$I(l) = \ \int_{a}^{l}{f(x) dx\ (l > a) }$

Аргумент l шексіздікке ұмтылағанда тиянақты шекке ұмтыла ма, міне, соны білуде. Жоғарыда атылған лемма бойынша бұл функцияның тиянақты шегі болу үшін төмендегі

$I(p) - I(q) = \ \int_{a}^{p}{f(x) dx -}\int_{a}^{q}{f(x) dx =}\int_{q}^{p}{f(x) dx}$

... жалғасы

I-тектi меншiксiз интегралдар

Меншіксіз интегралдар және олардың бас мәндері

II текті меншіксіз интегралдар. ( Шектелмеген функциялардан алынған интегралдар)

Математикалық талдаудың тура және кері есептері

Меншіксіз интегралдар туралы

Еселі интегралдардың қолданулары

Көп аргументті функциялардың интегралдық есептеулері

Жиындар мен математикалық логика элементтері. Дәрістер жинағы

Рационал сандар жиынының қасиеттері

Математикалық талдау

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс