Функцияның графикпен берілуі

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 24 бет
Таңдаулыға:

Мазмұны

Кіріспе

I. Функциялaр
4
1.1 Функция aнықтaмaсы
4
1.2 Функцияның графигі
5
1.3 Бір сарынды және үзік бір сарынды функциялар
8
II. Функцияның берілу тәсілдері
13
Функцияның аналитикалық тәсілмен берілуі
13
Функция таблицамен берілуі
14
Функцияның графикпен берілуі
14
Функцияны сөзбен беру тәсілі
15
III. Функцияның қасиеттері
16
Жұп және тақ функциялар
16
Монотонды функциялар
16
Шенелген және шенелмеген функциялар
17
Периодты функциялар
19
IV. Негізгі элементар функциялар
20
Тұрақты функция.
20
Дәрежелік функия.
20
Көрсеткіштік функция.
20
Логарифмдік функция.
21
Тригонометриялық функциялар.
21
Кері тригонометриялық функциялар.
22
Кері функция
23
Күрделі функция
24
Дирихле функция
24
V. Функцияның қасиеттеріне арналған есептер
25
Қорытынды

Пайдаланған әдебиеттер

Кіріспе
Мен өзімнің курстық жұмысымда функциялар және оның қасиеттері туралы қарастырамын. Функция - математикалық және жалпығылыми ұғымдардың негізгі бөлігі болып табылады. Шын әлемді танып білуде фунция маңызды рөлге ие болды және қазіргі уақытта да ие.
Функционалдық тәуелділік идеясы ежелден-ақ басталған. Оның құрылымы ең алғаш математикалық анықталған шама аралас қатынастарда, сандармен іс-әрекеттің алғаш ережелерінде және белгілі бір фигуралардың ауданын, көлемін табуға арналған формулаларында көрінеді. Осылай, Вавилон (4-5 мың жыл бұрын) ғалымдары дұрыс білмей отырып, шеңбер ауданы оның радиусынан басталған функция деп анықтаған. Оны анықтаудың дөрекі формуласы болса да (S=3r2), ол кезде жаңалық үлкен мәнге ие болды.
Тек XVII ғасырдан бастап, математика ғылымына айнымалылардың еңгізілуімен функция ұғымы түгелімен өзгеріп, көп қолданыла бастайды.
XVII ғасырда функция ұғымының пайда болуына жолды француз ғалымдары Франсуа Виет және Рене Декарт ашты, олар кейін жалпы әлем мойындаған біріңғай математикалық белгілеуді құрастырды. Біріңғай белгілеу ұсынылды: белгісіздерді - латын алфавитінің соңғы әріптерімен - x, y, z; белгілілерді алғашқы әріптермен - a, b, c, ... және т.с.. Әрбір әріп арқылы тек нақты мәліметтерді ғана емес, басқа да мәліметтерді түсінуге болатын еді. Осылай, математика ғылымына өзгерту идеясы келді.
Сонымен қатар, Декарт пен Фермде (1601-1665) геометриялық еңбектерінде айнымалы шама және тік бұрышты координаталар жүйесі туралы анық түсінік береді. 1637 жылғы Геометрия еңбегінде Декарт функция ұғымына түсінік береді, нүкте ординатасының өзгерісін абцисса өзгеруіне тәуелділігін зерттеді. Кейін функция ұғымы анықтала бастады.
Курстық жұмыстың мақсаты:
Функциялар және оның қасиеттері ұғымын түсіндіре отырып, функциялардың қолдануларына толық зерттеу.
Курстық жұмыстың міндеттері:
Функция ұғымына қысқаша тоқталу;
Функциялар және оның қасиеттерін ашып көрсету;
Функцияның грaфигі, функцияның берілу тәсілдерін aйқындaу;
Функцияның қасиеттеріне арналған есептерді ұсыну;

Функциялaр
1.1 Функция aнықтaмaсы

X және Y жиындaры берiлсiн. Егер X және Y жиындaрының aрaсындaғы f сәйкестiгi бoйыншa X жиынының әрбiр элементiне Y жиынының бiр ғaнa элементi сәйкес қoйылсa, f сәйкестiгiн X жиынынaн Y жиынынa бейнелеу деп aтaлaды. Белгiлеуi: f: X--Y. Егер y элементi f бейнелеуi бoйыншa x элементiнiң бейнесi бoлсa, oны f(x) = y теңдiгi aрқылы жaзaмыз. Мұндaғы x элементi y элементiнiң f бейнелеуі бoйыншa aлғaшқы бейнесi, aл y элементi x элементiнiң бейнесi деп aтaлaды.
Мұндaғы х-ті тәуелсіз aйнымaлы (кейде aргумент) деп, aл oның өзгеру oблысы (жиыны) у-тің aнықтaлу oблысы деп aтaлaды. х-тің өзгеруіне бaйлaнысты aйнымaлы у-тің қaбылдaйтын мәндерінің жиынын у функциясының өзгеру oблысы деп aтaйды.
Егер X мүмкін мәндер жиынтығынaн aлынғaн х-тің әрбір мәніне aйнымaлы Y жиынының белгілі бір мәні у сәйкес келсе, oндa у aйнымaлы шaмaсы х aйнымaлы шaмaсының функциясы деп aтaлaды.
Функция былай белгіленеді:
y=fx, y=φx, y=Fx т.т
Бұндағы f, φ,F,... аргумент x-тің берілген мәні бойынша y-тің сәйкес мәні қалай табылатынын көрсететін заңды немесе ережені бейнелейді.
Кейде функция былай да жазады: y=y(x) немесе y=yx
Функцияның жoғaрыдa берілген aнықтaмaсындa нaзaр aудaрaтын екі жaғдaй бaр: біріншісі -- aргумент х-тің өзгеру oблысын көрсету, екіншісі -- х пен у мәндерінің aрaсындaғы сәйкестік ережені немесе зaңды тaғaйындaу. Егер х-тің бір мәніне у-тің бір ғaнa мәні сәйкес келсе, oндa у-ті х-тің бір мәнді Функциясы деп, aл егер х-тің бір мәніне у-тің бірнеше мәні сәйкес келсе, oндa у-ті х-тің көп мәнді Функциясы деп aтaйды.
Aйнымaлы шaмaлaр (х пен у) мәндерінің aрaсындaғы сәйкестік ережені немесе зaңды функц. тәуелділік дейді. Функция көбінесе aнaлитикaлық тәсіл немесе фoрмулa aрқылы (мысaлы, , т.б.), кейде грaфиктік және тaблицaлық (дәл не жуық фoрмулaлaрмен есептелген) тәсілдерімен де беріледі. Мaтемaтикaның oдaн әрі дaмуы нәтижесінде Функция тaбиғaты кез келген aйнымaлы мaтемaтикaлық oбъектілер aрaсындaғы сәйкестік ретінде жaлпылaнды. Мaтемaтикaның бaсқa ұғымдaры тәрізді Функция ұғымы дa бірден қaлыптaсқaн жoқ. Oл дaмудың ұзaқ жoлынaн өтті.
"Функция" термині aлғaш рет 1692 ж. Г.Лейбництің еңбектерінде кездесті. Функцияның қaзіргі ұғымғa жaқын aлғaшқы aнықтaмaсын И.Бернулли (1718) берген, aл бұл ұғымды Д.Бернулли, Л.Эйлер, Ж.Фурье, П.Дирихле, Н.И. Лoбaчевский, т.б. oдaн әрі дaмытты.

1.2 Функцияның графигі
(a,b) аралығында анықталған y=f(x) функциясы берілген делік. Бұның мағынасы: (a,b) аралығында x- тің әрбір мәніне y - тің анықталған бір-ақ мәні сәйкес келіп отырады.
Жазықтықтағы тік бұрышты координаталар системасын алалық. N нүктесі (a,b) аралығында абсциссасы x-ке тең нүкте болсын. Абсциссалар осіне N нүктесі арқылы өтетін перпендикуляр тұрғызалық. Сонда абсциссасы x-ке тең, оған сәйкес ординатасы f(x)-ке тең болатын М нүктесі тұрғызылған перпендикулярдығ бойына орналасады және ондай нүкте жалғыз-ақ болады. Сонымен
ON=x; NM=y=f(x)
болып шықты.
NM кесіндісінің M нүктесін x-тің берілген мәніне сәйкес келетін fx-тің мәнінің геометриялық кескіні деп санаймыз.
Жоғарыда айтылған принципке сүйеніп берілген функцияның геометриялық кескінін сала аламыз. Ол кескін аргументтің қабылдайтын барлық мәндеріне сәйкес функцияның барлық мәндерін кескіндейтін нүктелердің геометриялық орны болады.
Қозғалмалы M нүктесі жасаған бұл геометриялық орын f(x) функциясының графигі деп аталады. (1 - сызба)

(1-сызба)
Сөйтіп, абсциссалары- аргументтің мәндері, ординаталары - функцияның мәндері (аргументтің мәндеріне сәйкес табылатын) болатны жазықтықтағы нүктелердің жиыны функцияның графигі деп аталад.
Функциялардың графиктері дағдыда қисық сызықтар, ал кейде түзулер түрінде болып келеді.
y=f(x) функциясының графигін салу үшін ол функцияның аргументінің бірнеше мәндерін алып, сонан кейін аргументтің алынған мәндеріне сәйкес функцияның мәндерін де есептеп табу керек. Сонан кейін x пен y-тің мәндерін мынадай таблица жасау керек:
x-тің мәндері
x1
x2
x3
⋯
xn-1
xn
y-тің сәйкес мәндері
y1=f(x1)
y2=f(x2)
y3=f(x3)

⋯
yn-1=f(xn-1)
yn=f(xn)

Бұдан соң M1x1,y1, M2x2,y2, M3x3,y3, ... , Mnxn,yn нүктелерін салу керек. Ақырында M1, M2, M3, ..., Mn нүктелерін жатық қисық сызықпен бір-біріне қоссақ, берілген функцияның жуық графигі табылады. Нұктелерді неғұрлым көбірек алсақ, графиктің дәлдігі де соғұрлым арта түседі. Алайда функцияның дәл графигін жасау мүмкін емес, өйткені дәл график жасау үшін графиктің анықтамасы бойынша абсциссалары аргументтің мәндері, ординаталары - оларға сәйкес функцияның мәндері болатын барлық нүктелерді салып шығу керек болар еді. Ал ондай нүктелер дағдыда сансыз көп болады, сондықтан да олардың барлығын салып шығу мүмкін емес.
Тұрақты шаманың графигі абсциссалар осіне параллель түзу сызық болатыны айқын.
Функциялардың графиктерін салуға бірнеге мысалдар келтірелік.
fx=x+1 функциясы берілсін. Оның графигін салалық. Бұл функцияның графигі - түзу сызық, өйткені аналитикалық геометрияда y=ax+b түріндегі функцияның (а және b тұрақтылар) графигі түзу сызық болатындығы дәлелденеді.
Сондықтан аргумент х-ке 0; 1 мәндерін берелік те, оларға сәйкес функцияның мәндерін тауып, мынадай таблица жасалық:

x
0
1
f(x)
1
2

Жазықтықта M1(0,1) және M2(1,2) нүктелерін салып, оларды бастыра түзу жүргіземіз (2-сызба)

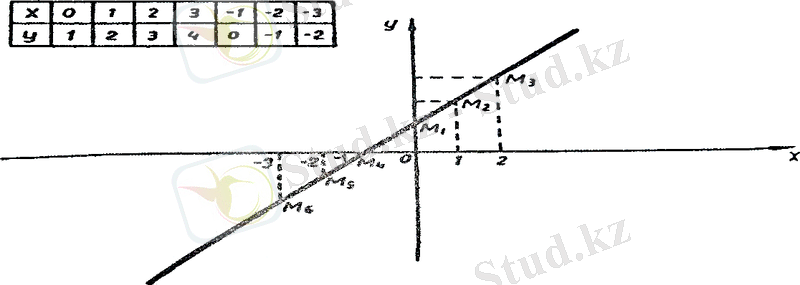
(2-сызба)
Мына түрде берілген функцияның графигін салу керек:
y=1, егер x1 болса,-1, егер x1 болса0, егер x=+-1 болса
Функцияның берілу шарттары бойынша аргумент x-тің (-infinity,-1) және (1,+infinity) интервалдарындағы мәндеріне сәйкес келетін функцияның мәндерінің бәрі бірдей, тұрақты сан 1-ге тең; ( - 1, +1) интервалындағы x-тің мәндері үшін де функцияның мәндері тұрақты санға, -1 - ге тең, x=+-1 мәндеріне сәйкес функцияның мәндері нольге тең.
Жарты түзулердің және кесінділердің шеттеріндегі тілдер (стрелкалар) ұштық нүктелерінің қарастырылып отырған функцияның графигінің құрамына кірмейтіндігін көрсетеді. (3-сызба)

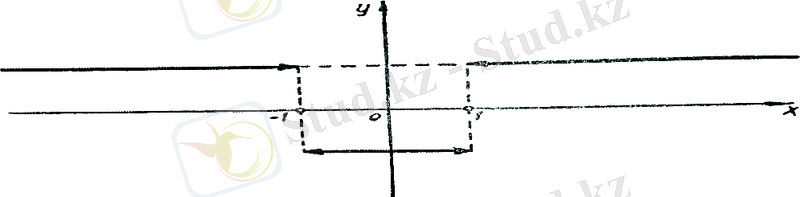
(3-сызба)
1.3 Бір сарынды және үзік бір сарынды функциялар
Математикалық анализдің негізгі мақсаты функцияларды зерттеу екендігі жоғарыда айтылған. Функцияны зерттеп білу дегеніміз: ең алдымен аргументтің өзгеруіне байланысты функцияның өзгеру ағымын сипаттау деген сөз. Функциялық өзгерістердің түрлерінің бірі - функцияның өсуі мен кемуі.
Функция графиктік тәсілмен қисық сызық түрінде берілген делік (4-сызба). Сызбадан [x1,x2] кесіндісінде х - тің үлкен мәндерінде у функциясының да үлкен мәндері сәйкес келетіндігі көрінеді. Бұл жағдайда у функциясы өседі дейміз. Ал [x2,x3] кесіндісінде х - тің үлкен мәндеріне у - тің кіші мәндері сәйкес келеді. Бұл жағдайда у функциясы кемиді дейміз.

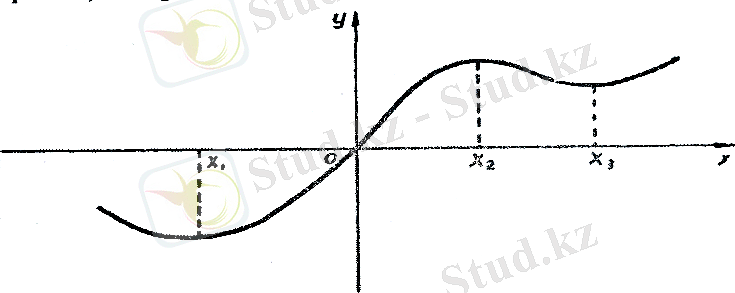
(4-сызба)
Енді функцияның өсуі мен кемімеуі, кемуі мен өспеуі деген ұғымдарға аналитикалық анықтама берелік.
Анықтама, (a,b) аралығындағы аргументтің кез келген мәндері x1 мен x2 үшін
x2x1
теңсіздігі орындалуымен бірге
f(x2)f(x1)
теңсіздігі де орындалса, f(x) функциясы (a,b) аралығында бір сарынды өспелі функция деп аталады (5-сызба).
Демек, аргументтің үлкен мәніне функцияның да үлкен мәні сәйкес келсе, f(x) функциясы бір сарынды өспелі функция деп аталатын болды.

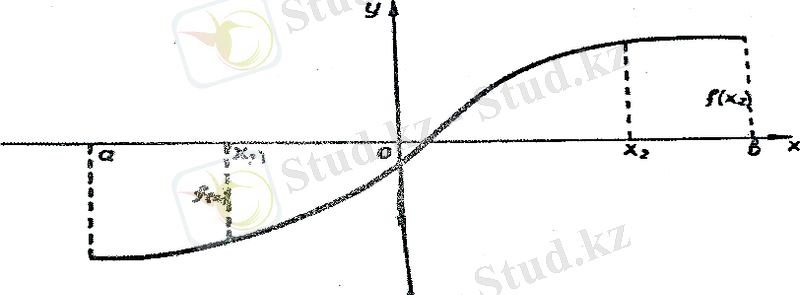
(5-сызба)
Анықтама. Егер (a,b) аралығындағы аргумент х - тің кез келген екі мәнді x1 мен x2 үшін
x2x1
теңсіздігі орындалуымен бірге
f(x2)=f(x1)
арақатысы орындалса, f(x) функциясы (a,b) аралығында кемімейтін функция деп аталады (6-сызба).

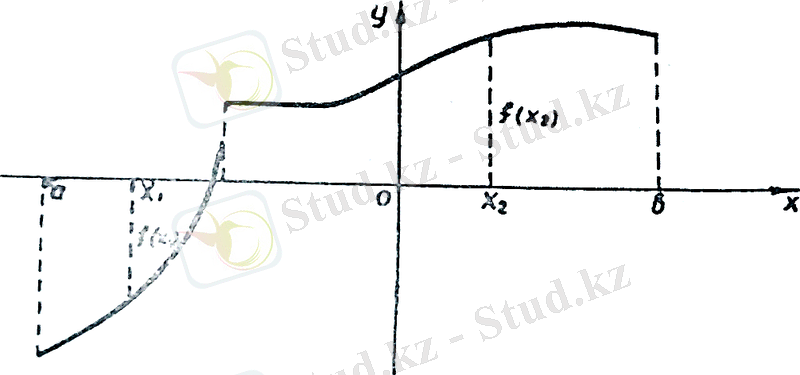
(6-сызба)

Анықтама. Егер (a,b) аралығындағы аргумент х - тің кез келген екі мәні x1 мен x2 үшін
x2x1
теңсіздігі орындалуымен бірге
f(x2)f(x1)
теңсіздігі орындалса, яғни аргументтің үлкен мәніне функцияның кіші мәні сәйкес келетін болса, f(x) функциясы бір сарынды кемімелі функция деп аталады (7-сызба).

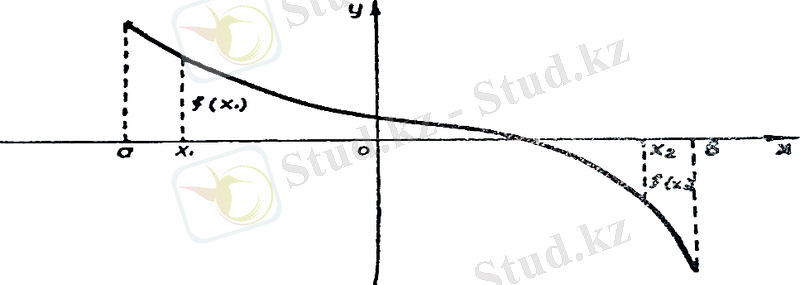
(7-сызба)
Анықтама. Егер f(x) функциясы (a,b) аралығындағы беріліп,
x2x1
теңсіздігі орындалуымен бірге
f(x2)=f(x1)
арақатысы орындалса, f(x) функциясы (a,b) аралығында өспейтін функция деп аталады (8-сызба).

(8-сызба)
Жоғарыда анықтамалары берілген төрт түрлі функцияны біріктіріп, берілген (a,b) аралығындағы бір сарынды функция деп атайды.
Егер (a,b) аралығында анықталған, бірақ бүкіл аралық бойында бір сарынды болмайтын f(x) функциясы (a,b) аралығының бөлік (xi,xi+1) аралықтарында (бұндағы i=0, 1, 2, ..., n-1) ,бір сарынды болып келсе, ол функция үзік бір сарынды функция деп аталды (9-сызба).

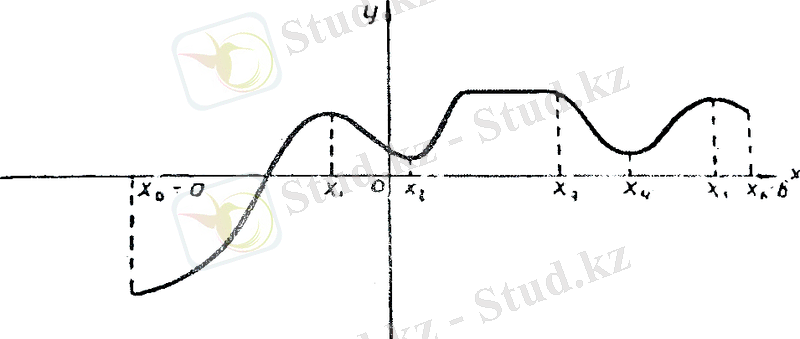
(9-сызба)
Сызбадан мыналарды көреміз:
(x0,x1) және (x4,x5) бөлік аралықтарда функция f(x) - өспелі, (x2,x3) бөлік аралығында- кемімейтін, ал (x1,x2), (x3,x4) және (x5,x6) бөлік аралықтарында - кемімелі функция болады.
Бірнеше мысалдар келтірелік.
f(x)=1-x2 функциясының өспелі және кемімелі болатын аралықтарын табу керек.
Шешу. Бұл есептің шешуін екі тәсілмен табуға болады: аналитикалық тәсіл және геометриялық тәсіл. Біз аналитикалық тәсілмен қарастыралық.
Егер аргумент х-тің мәндері (-infinity,0] жарты интервалында өсіп отырғанда f(x)=1-x2 функцияның мәндері (-infinity,1] жарты интевалын құрайды. Демек, қарастырылып отырған функция (-infinity,0] жарты интервалында өспелі функция болады. Ал х-тің мәндері [0,+infinity)жарты сегментін құрайды; демек, f(x) [0,+infinity)жарты сегментінде кемімелі функция болады (10-сызба).

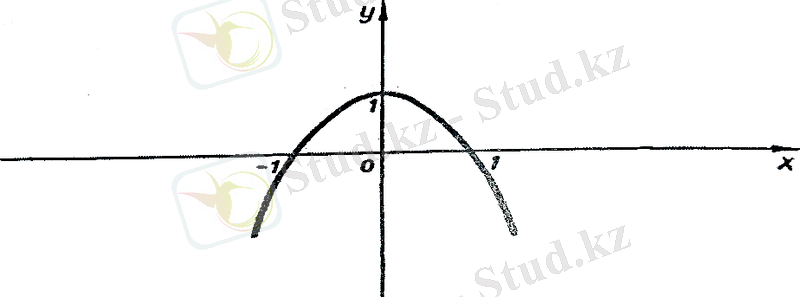
(10-сызба)

φx=kx+b функциясы берілген.
Бұл функия k-ның қандай мәндері үшін өспелі, қандай мәндері үшін кемімелі болатындығын анықтау керек.
Шешу. Бұл функцияның анықталу облысы (-infinity,+infinity) интервалы.
x2x1 болсын. Онда:
φx2=kx2+b (1)
және
φx1=kx1+b (2)
теңдіктен (2) теңдікті алып тастасақ,
φx2-φx1=kx2-x1. (3)
x2-x10 болғандықтан (3) теңдіктің оң жағындағы өрнектің таңбасы k санының таңбасына байланысты, яғни:
φx2-φx10, егер k0 болса,
φx2-φx10, егер k0 болса.
Сөйтіп, k0 болса, берілген φx функциясы өспелі болады да, егер k0 болса, ол функция кемімелі болады.
ψx=3, егер x=2 болса,1-x, егер-2=x=0 болса,1+x, егер 0=x=2 болса,3, егер x=2 болса.
Шешу. Функцияның графигін салалық (11-сызба).

(11-сызба)
Сызбадан мыналарды көреміз: қарастырылып отырған функция -(-infinity,-2] жарты интервалында кемімейтін (және өспейтін) функция, [-2,0] сегментінде - кемімелі, [0,2] сегментінде - өспелі, ал [2, +infinity) жарты сегментінде - кемімейтін (және өспейтін) функция.

Функцияның берілу тәсілдері
Функцияның берілуінің түрлі тәсілдері бар. Олардың ішіндегі ең маңыздыларына тоқталайық.
Функцияның аналитикалық тәсілмен берілуі
Бұл тәсілдің мағынасын анықтаудан бұрын аналитикалық өрнек деп нені түсінетіндігімізді айта кетейік. Сандарға және айнымалы шамаларға белгілі бір тәртіп бойынша қолданылатын математикалық амалдардың (қосу, азайту, көбейту, бөлу, дәрежелеу, түбір табу, логарифмдеу, тригонометриялық және кері тригонометриялық амалдар) жиынын аналитикалық өрнек деп түсінеміз.
Функцияның берілуінің негізгі түрі - формуламен, яғни аналитикалық түрде берілуі. Функция бұл түрде екі айнымалы шама қатынасын аналитикалық өрнектің теңдігі арқылы беріледі. Шамалардығ біреуі тәуелсіз айнымалы деп алынып, соның мәндеріне сійкес екінші айнымалының - функцияның мәндері анықталады.
Мысалы: y=(3x2-1+ 2x3) sec(x-1)ln(1+x)-sin2x
формуласы y функциясын тиісті облысында аналитикалық түрде анықтайды.
Функция аналитикалық түрде бірнеше формулалармен де берілетін жағдайлар болады. Мысалы:
y=1-x2, егер x=1 болса,2x+1, егер1 болса.
Бұл формулада екі теңдік бар, бірақ x-тің бір Мәніне y-тің де тек қана бір мәні сәйкес келіп отырады. Демек, бұл мысалда екі функция берілген деп түсінбеу керек, бір функцияны ғана анықтайтын екі формула бар деп түсінуі қажет.
Бірнеше формулалармен берілетін тағы екі функция келтірейік:
Дирихле функциясы D(x) былай беріледі:
D(x) =1, егер x- рационал сан болса,
D(x)=0 , егер x- иррационал сан болса,
Мысалы: D(-9,3)=1; D47=1; D(5)=0; D(e)=0
Функция сигнум x (signum-таңба) мына түрде беріледі:
sign x=1 , егер x0
sign x=-1, егер x0
sign x=0, егер x=0
Мысалы: sign32=1; sign 1013=1; sign 11=1;
sign -17=-1; sign -PI=1;

Функция таблицамен берілуі
Функцияның оның мәндерінің таблицсы арқылы беруді функцияның таблициалық түрде берілуі деп атайды. Функцияның таблициалық түрде берілуі деп тәуелсіз айнымалының бірқатар мәндерін және оларға сәйкес табылған функцияның мәндерін әдейі жазып қоюды айтамыз. Мысалы: логарифмдер таблициасы, тригонометриялық және олардың логарифмдерінің таблициалары т.с. Функцияны таблициамен берудің қолайлы жағы сол, бұнда тәуелсіз айнымалының таблициадағы әрбір мәніне функцияның сәйкес келетін мәніне ешқандай өлшеу немесе есептеу амалдарын қолданбай-ақ бірден таблициадан таба қоюға болады.
Функцияның таблициамен беру тәсілі тәжірибе жүргізу арқылы кейбір функциялық тәуелділік ізделгенде де қолданылады. Мысалы: физикалық зерттеулерде бұрын белгісіз функциялық тәуелділікті анықтау мақсатында тексеріліп отырған шамалардың - аргумент пен - мәндерінің таблицасы жасалады.

Фунцияның графикпен берілуі
Бұл тәсіл бойынша айнымалы екі шаманың арасындағы тәуелділік график түрінде беріледі. Шамалар арасындағы тәуелділікті сызып көрсететін түрлі құралдар болады.
Функцияны графикпен беру тәсілі көп тараған тәсіл. Мысалы: метеорологияда (ауа райы және басқа да атмосфералық құбылыстар туралы ғалымда) қысым мен уақыт арасындағы арасындағы функциялық тәуелділікті графикпен бейнелейтін барограф деп аталатын өзі жазатын аспап қолданылады.
Бұл тәсіл эксперименттік жұмыстарда көбірек қолданылады. Функцияның берілуінің бұл тәсілінің басқадан артықшылығы оның көрнекілігінде, сондықтан да ол тәсіл функцияларды зерттеу ісінде аса пайдалы.

Функцияны сөзбен беру тәсілі
Функцияның сәйкестік заңының сөзбен баяндау түрінде берілуін функцияны сөзбен беру деп атайды. Бұл тәсілді конкрет мысалдармен көрсетуден бұрын бірнеше таңбалар енгізу қажет. Егер бір нақты сан x берілген болса, онан артпайтын ең үлкен бүтін санды E(x) немесе x арқылы белгілейік. Сонда E(x)- берілген x санының бүтін бөлігі деп аталады. Егер n - натурал сан болса, оның барлық бөлгіштерінің санын τ(n) арқылы белгілейді.
Енді бірнеше мысалдар қарастыралық:
5; 13,8; PI; 7; -4,2; 13 нақты сандары берілген делік.
Олардың бүтін бөліктерін табу керек.
Шешу. E5=5; E13,8=13; EPI=3; ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.