Тізбектің шегі туралы теоремалар

Мазмұны

Кіріспе

Мен өзімнің курстық жұмысымда Шек табудың тәсілдері туралы қарастырамын. Шектердің қазіргі теориясы XIX ғ- дың басында қалыптаса бастады. Шек ұғымы алғаш рет О. Коши еңбектерінде қолданылды. Тізбек пен функция шектерінің теориясы Б. Больцано мен К. Вейерштрасстың еңбектері негізінде қалыптасты.

Шек ұғымы математикалық талдауда іргелі ұғым болып табылады. Шек жөнінде алғашқы мағұлмат сонау мектеп курсында кездеседі. Мәселен, алгебрада шек ұғымы шексіз кемімелі геометриялық прогрессияның мүшелер қосындысымен байланысса, геометрияда, шек ұғымы шеңбердің ұзындығын дөңгелек және бет ауданын, дене көлемін есептеумен байланысады.

Математикалық талдау курсында шек арқылы туынды, анықталған интеграл ұғымдары енгізіледі. Ең алдымен сандық тізбек ұғымымен танысып, келесі мысалдарды қарастырайық.

Анықтама. Егер әрбір натурал санға n = 1, 2, … қандай да бір заңдылықпен $x_{n}$ нақты саны сәйкес қойылса, онда $x_{1}$ , $x_{2}$ , . . . , $x_{n}$ , . . . сандар тізбегі анықталған дейді де былай белгіленеді

$\left\{ x_{n} \right\}$ = $\left\{ x_{1}{, \ x}_{2}{, \ldots, x}_{n}, \ldots \right\}$ , (1)

Мұндағы әрбір $x_{n}$ саны (1) тізбектің элементі немесе мүшесі деп аталады.

Тізбекке мысалдар:

1. {1, 12, 13, …}\left\{ 1, \ \ \frac{1}{2}, \frac{1}{3}, \ldots \right\}={1n}\left\{ \frac{1}{n} \right\}.
2. {12, 2, 12, 2, …}\left\{ \frac{1}{2}, \ 2, \ \frac{1}{2}, \ 2, \ldots \right\}={2(−1) n}\left\{ 2^{{( - 1) }^{n}} \right\}.
3. {−1, 2, −3, 4, …}\left\{ - 1, \ 2, \ - 3, \ 4, \ldots \right\}={(−1) nn}\left\{ {( - 1) }^{n}n \right\}.
4. {2, 5, 10, …}={n2+1}\left\{ 2, \ 5, \ 10, \ldots \right\} = \left\{ n^{2} + 1 \right\}.

Мақсаты : Шек табудың әр түрлі тәсілдерін анықтау.

Міндеті : Шектер теориясымен танысып, тізбектің және функцияның шектерін қарастырып, оларға мысалдар келтіру.

1 Тізбектің шегі

1. 1 Сандық тізбек және оның берілу тәсілдері

Сандық тізбек деп N натурал сандар жиынында анықталған сандық функцияны (немес N жиынының $\mathsf{R}$ жиынына бейнеленуін) атайды. Бұл функцияның f әріпімен белгілейік. Сонда анықтама бойынша 1 санына $f$ (1) мәні, 2 санына $f$ (2) мәні т. с. с. сәйкес келеді. Жалпы алғанда ондай сәйкестікті былай белгілейді:

n → $f$ (n) .

Бұл шамаларды сәйкес түрде $f_{1}$ = $f$ (1), $f_{2}$ = $f$ (2), …, $f_{n}$ = $f$ (n), … арқылы белгілеп, оларды тізбектің бірінші, екінші, және т. с. с. n - ші мүшелері деп атайды, n - ші мүшені тізбектің жалпы мүшесі дейді. Жалпы мүшесі $f_{n}\$ болатын тізбекті $\left\{ f_{1}{, f}_{2}, \ldots, f_{n}, \ldots \right\}$ немесе $\left\{ f_{n} \right\}$ арқылы белгілейді. Осылайша белгілеуде n номері N натурал сандар жиынының барлық мәндерін қабылдайды деп түсініледі.

Тізбекті жазып берудің жиі қолданылатын тәсілдері мыналар:

1. Аналитикалық тәсіл. Бұл тәсілді қолданғанда n номері бойынша тізбектің сәйкес мүшесін табу үшін формула жазылып көрсетіледі.

Мысалдар: 1. $x_{n}$ = 1+ $\frac{1}{2^{n}}$ $(n) \ (n\ \ N)$ . Бұл формула бойынша

$x_{1}\$ = 1 + $\ \frac{1}{2}$ = $\frac{3}{2}$ , …, $\ \ \ \ x_{5}$ = 1 + $\frac{1}{2^{5}}$ = 1+ $\frac{1}{32}$ = $\frac{33}{32}$ , т. с. с. Бұл жағдайда $\left\{ x_{n} \right\}$ тізбегі

$x_{n}$ = 1 + $\frac{1}{2^{n}}$ формуласымен берілген дейік.

2. $x_{n}$ = 3, n N. Бұл тізбектің барлық мүшелері бір- бірімен тең. Барлық мүшелері өзара тең болатын тізбекті тұрақты тізбек деп атайды.

3. Тізбекке тағы мынадай мысалдар келтірейік:

$\left\{ n \right\}$ = $\left\{ 1, \ 2, \ 3, \ldots, n, \ldots \right\}$ ; $\left\{ \frac{1}{n} \right\}$ = $\left\{ 1, \ \ \frac{1}{2}, \ \frac{1}{3}, \ldots, \frac{1}{n}, \ldots \right\}$ ;

$\left\{ 1 + \ \frac{1}{10^{n}} \right\}$ = $\left\{ 1, 1; 1, 01; 1, 001; \ldots; 1 + \frac{1}{10^{n}} \right\}$ ; $\left\{ \frac{n - 1}{n} \right\}$ = $\ \left\{ 0, \ \ \frac{1}{2}, \frac{2}{3}, \ldots \right\}$ .

2. Рекурренттік тәсіл. Бұл тәсілді қолданғанда тізбектің бірінші мүшесі беріледі және осы тізбектің белгілі бір неме бірнеше алғашқы мүшелері бойынша кез- келген мүшесін табу үшін формула беріледі.

Мысал. а) кез келген n ≥ 2 үшін $a_{n}$ = $a_{n - 1} + d$ ; б) кез- келген n ≥ 2 үшін $b_{n}$ = $b_{n - 1}*q$ ; а) және б) формулалары сәйкес $\left\{ a_{n} \right\}$ және $\left\{ b_{n} \right\}$ тізбектерінің берілген алдыңғы мүшесі бойынша оның кез келген мүшесін (екінші мүшесінен бастап) табуға мүмкіндік береді. Бұл тізбектер арифметикалық және геометриялық прогрессиялар түрінде бізге бұрыннан таныс болатын. Тізбектің рекурренттік тәсілмен берілуі шапшаң есептейтін электрондық есептеуіш машиналармен жұмыс істегенде аса қолайлы келеді; сонда машина әрі жеңіл, әрі шапшаң орындалатын біріңғай есептеу операцияларын бірнеше рет қайталайтын болады.

3. Баяндап беру тәсілі. Бұл тәсілді қолданғанда тізбек элементтері баяндап айтылатын болады. Бұл жағдайда тізбектің жалпы мүшесі үшін формула да, немесе оның мүшелері үшін рекуренттік қатыс та белгісіз болуы мүмкін. Осы айтылғанды мысалмен түсіндіру үшін мына тізбектерді қарастырайық.

а) 2, 3, 5, 7, 11, . . . ; б) 2; 2, 2; 2, 23; 2, 236; 2, 2361; . . . Бұл тізбектерді былайша баяндайды: бірінші тізбек жәй сандар тізбегі, ал екіншісі $\sqrt{5}$ саны үшін кемімен алынған ондық жуықтаулар тізбегі.

$\left\{ y_{n} \right\}$ тізбегін графикпен бейнелегенде мынадай екі тәсіл қолданылады:

1) $\left\{ y_{n} \right\}$ тізбегін фуекция деп алып, оны координаталық жазықтықтың $M$ ( $n, \ y_{n}$ ) нүктелерінің жиыны арқылы бейнелуге болады;

2) $\left\{ y_{n} \right\}$ тізбегін координаталық түзудің $M$ ( $y_{n}$ ) (немесе $y_{n}\$ ) нүктелерімен бейнелеуге болады.

$y_{n}$ = $\frac{1}{n}$ тізбегін бейнелеудің осы екі тәсілі де 28, 29- суреттерде көрсетілген.

1. 2 Тізбек шегін анықтау

1- анықтама . Егер кез келген оң ԑ санына сайкес натурал $n_{Ɛ}$ саны табылып, барлық $\ n\$ ˃ ${\ n}_{ԑ}$ номерлері үшін $\left x_{n} - a \right$ ˂ ԑ теңсіздігі орындалса, онда $a\$ саны $\left\{ x_{n} \right\}$ тізбегінің шегі деп аталады және былай жазылады: $\lim_{n \rightarrow \infty}x_{n}$ = $a$ немесе n→∞ (символдар арқылы: $\lim_{n \rightarrow \infty}x_{n}$ ⇔∀ԑ ˃ 0Ǝ ${\ n}_{ԑ}$ ǀn˃ ${\ n}_{ԑ}$ ⇒ǀ $x_{n} - a$ ǀ˂ԑ) . Шегі бар болатын тізбек жинақталатын тізбек деп, ал шегі болмайтын тізбек жинақталмайтын тізбек деп аталады. Модуль қасиетінің негізінде ǀ $x_{n} - a$ ǀ˂ԑ теңсіздігі -ԑ ˂ $x_{n} - \ a˂\ ԑ$ немесе $a - ԑ$ ˂ $x_{n}˂$ $a + ԑ$ теңсіздігімен пара пар, олай болса, барлық $n\$ ˃ ${\ n}_{ԑ}$ үшін $x_{n} \in$ $U_{ԑ}$ (a), яғни $a\$ нүктесінің ԑ- маңайы тізбектің $n\$ ˃ ${\ n}_{ԑ}$ нөмірлі барлық мүшелерін қамтиды. Бұдан тізбек шегінің тағы бір анықтамасына келеміз.

2- анықтама. Егер $a$ нүктесінің кез- келген ԑ маңайы $\left\{ x_{n} \right\}$ тізбегінің саны арқылы $\left\{ x_{1}{, x}_{2}{, \ldots, x}_{n_{ԑ}} \right\}$ мүшелерінен өзге барлық мүшелерін қамтитын болса, онда осы $a\$ санын $\left\{ x_{n} \right\}$ тізбегінің шегі деп атайды (30- сурет) .

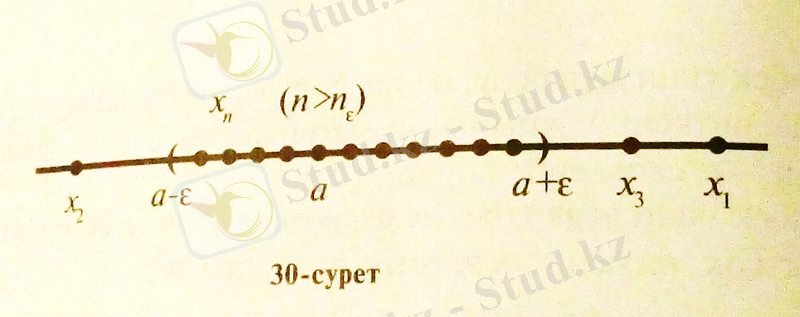
Мысалдар. 1. $\left\{ \frac{n - 1}{n + 1} \right\}$ тізбегі жинақталады және оның шегі 1 - ге тең. Шынында да, шек анықтамасының орындалатындығын тексерейік. Ол үшін $\left \frac{n - 1}{n + 1} - 1 \right\$ ˂ ԑ теңсіздігін қарастырайық. Кейбір түрлендірулерді орындай келе мынаны табамыз:

$\left \frac{n - 1}{n + 1} - 1 \right\$ ˂ ԑ⇔ $\left \frac{2}{n + 1} \right\$ ˂ ԑ ⇔ $\ \frac{n + 1}{2}$ ˃ $\frac{1}{ԑ}$ ⇔ $n$ ˃ $\ \frac{2}{ԑ}$ - 1.

Демек, натурал ${\ n}_{ԑ}$ саны табылып, (мысалы, $\ \frac{2}{ԑ}$ -1 санының бүтін бөлігіне тең), барлық $n\$ ˃ ${\ n}_{ԑ}$ = $\left\lbrack \ \frac{2}{ԑ}\ - \ 1 \right\rbrack$ нөмірлері үшін $\left \frac{n - 1}{n + 1} - 1 \right\$ ˂ ԑ теңсіздігі орындалады, яғни $\lim_{n \rightarrow \infty}\frac{n - 1}{n + 1}$ = 1. Енді ԑ = 0. 01 және ԑ = 0. 001 мәндеріне сәйкес ${\ n}_{ԑ}$ мәндерін табайық.

а) ԑ = 0. 01 ; ${\ n}_{ԑ}$ = (2 ^. $10^{2} - \$ 1) = 200 - 1= 199; ${\ n}_{ԑ}$ = 199.

б) ԑ = 0. 001 ; ${\ n}_{ԑ}$ = (2 ^. $10^{3} - \$ 1) = 2000 - 1= 1999;

$n \rightarrow \infty$ жағдайда $\frac{n - 1}{n + 1}\$ бөлшегі бірден кіші мәндерді қадһбылдай отырып, өсе келе 1 санына ұмтылады, яғни $\frac{n - 1}{n + 1}$ → 1.

2. $\lim_{n \rightarrow \infty}\frac{\cos\frac{\pi}{2}n}{n}$ = 0. Шынында да, $\left \frac{\cos\frac{\pi}{2}n}{n} - 0 \right$ ≤ $\ \frac{1}{n}$ < ԑ ⇔ $\frac{1}{ԑ}$ . Демек, $n\$ ˃ ${\ n}_{ԑ}\$ = $\left\lbrack \ \frac{1}{ԑ} \right\rbrack$ ⇔ $\left \frac{\cos\frac{\pi}{2}n}{n} - 0 \right$ < ԑ . $n \rightarrow \infty\$ жағдайда $\frac{\cos\frac{\pi}{2}n}{n}$ бөлшегі 0- ге тең де, одан кіші де мәндерді қабылдай отырып, өзінің шегі 0- ге ұмтылады .

3. $\left\{ \cos\frac{\pi}{2}n \right\}$ жинақталмайтын тізбек болады. Шынында да, $a\$ нүктесінің ԑ- маңайының сыртында осы тізбектің сансыз көп мүшелері жатады. Сондықтан $a\$ саны тізбектің шегі бола алмайды.

1. 3 Тізбектің шегі туралы теоремалар

1- теорема. Егер $\left\{ x_{n} \right\}$ және $\left\{ y_{n} \right\}$ тізбектері жинақталатын болса, онда $\left\{ x_{n} \pm y_{n} \right\}$ тізбектері де жинақталатын болады және $\lim_{n \rightarrow \infty}{(x_{n} \pm y_{n}) }$ = $\lim_{n \rightarrow \infty}x_{n}$ + $\lim_{n \rightarrow \infty}y_{n}$ , яғни жинақталатын екі тізбек қосындысының шегі сол тізбектер шектерінің қосындысына тең болады.

Дәлелдеуі. $\ \ \ \lim_{n \rightarrow \infty}x_{n}$ = $a$ $\underset{n \rightarrow \infty}{және\ \ \ lim}y_{n} = b$ дейік. Сонда1- теорема (6-п. ) негізінде $x_{n} = a$ + $\alpha_{n}$ , $y_{n} =$ b + $\beta_{n}$ (мұндағы $\left\{ \alpha_{n} \right\}$ мен $\left\{ \beta_{n}\ \right\}$ ақырсыз кіші тізбектер) теңдіктерін аламыз. Бұдан ${\ \ \ x}_{n} \pm y_{n}$ = $(a$ + $b)$ + ( $\alpha_{n} + \ \beta_{n}) .$ $\left\{ x_{n} \pm y_{n} \right\}$ тізбегі 1- лемма негізінде ақырсыз кіші тізбек, яғни $\lim_{n \rightarrow \infty}{(x_{n} \pm y_{n}) } = \$ 0. Сонда 6- пункттің 1- теоремасы бойынша $\lim_{n \rightarrow \infty}{(x_{n} \pm y_{n}) }$ = $\lim_{n \rightarrow \infty}x_{n}$ + $\lim_{n \rightarrow \infty}y_{n}. \$ Бұл теореманы индукция әдісін қолдана отырып, саны шектеулі тізбектердің алгебралық қосындысы үшін де дәлелдеуге болады.

2- теорема. Егер $\left\{ x_{n} \right\}$ және $\left\{ y_{n} \right\}$ жинақталатын тізбек болса, онда $\left\{ x_{n} \bullet y_{n} \right\}$ тізбегі де жинақталатын болады және $\lim_{n \rightarrow \infty}{(x_{n} \bullet y_{n}) }$ = $\lim_{n \rightarrow \infty}x_{n}$ ∙ $\lim_{n \rightarrow \infty}y_{n},$ яғни жинақталатын тізбектер көбейтіндісінің шегі олардың шектерінің көбейтіндісіне тең болады.

Дәлелдеуі. $\lim_{n \rightarrow \infty}x_{n}$ = $a$ $\underset{n \rightarrow \infty}{және\ \ \ lim}y_{n} = b$ болсын, сонда $x_{n} = a$ + $\alpha_{n}$ , $y_{n} =$ b + $\beta_{n}$ (мұндағы $\left\{ \alpha_{n} \right\}$ мен $\left\{ \beta_{n}\ \right\}$ ақырсыз кіші тізбектер) . Мына көбейтіндіні қарастырайық:

$x_{n} \bullet y_{n}$ = $(a$ + $\alpha_{n})$ ( $b + \ \beta_{n}) \$ = $ab + (a\beta_{n} + b\alpha_{n} + \alpha_{n}\beta_{n})$ ; $\left\{ a\beta_{n} + b\alpha_{n} + \alpha_{n}\beta_{n} \right\}$ тізбегі 1 және 2- леммалар негізінде ақырсыз кіші тізбек болып табылады. Сонымен, барлық n ∈ N үшін $\ x_{n} \bullet y_{n}$ = $ab + (a\beta_{n} + b\alpha_{n} + \alpha_{n}\beta_{n})$ , $\underset{n \rightarrow \infty}{\ \ \ lim}{(a\beta_{n} + b\alpha_{n} + \alpha_{n}\beta_{n}) }$ = 0. Ал бұдан мына теңдік шығады (1- теореманы қараңыз) :

$\lim_{n \rightarrow \infty}{(x_{n} \bullet y_{n}) }$ = $\lim_{n \rightarrow \infty}x_{n}$ ∙ $\lim_{n \rightarrow \infty}y_{n}$ .

Ескерту. Егер барлық n ∈ N үшін $\ x_{n}$ = С болса, онда $\lim_{n \rightarrow \infty}x_{n}$ = $\lim_{n \rightarrow \infty}С$ =С немесе тұрақты санның шегі десол тұрақты сан болады. Шынында да, $x_{n} - С = С - С = 0$ болғандықтан, $\left\{ x_{n} - С \right\}$ ақырсыз кіші тізбек, сондықтан 1- теорема бойынша $\lim_{n \rightarrow \infty}x_{n}$ = $С$ .

1- салдар. Егер $\left\{ x_{n} \right\}$ тізбегі жинақталатын болса, онда кез келген С саны үшін $\left\{ {С \bullet x}_{n} \right\}$ тізбегі де жинақталатын тізбек болады және $\lim_{n \rightarrow \infty}{С \bullet x}_{n} =$ $\lim_{n \rightarrow \infty}С$ ∙ $\lim_{n \rightarrow \infty}x_{n}$ $=$ $\underset{n \rightarrow \infty}{С \bullet lim}x_{n}$ , яғни тұрақты көбейткішті шек таңбасының алдына шығаруға болады.

2- салдар. Егер $\left\{ x_{n} \right\}$ тізбегі жинақталатын тізбек, ал k- натурал сан болса онда

$\lim_{n \rightarrow \infty}x_{n}^{k}$ = ${(\lim_{n \rightarrow \infty}x_{n}) }^{k}$ .

Бұл салдарды 2- теоремадан индукция әдісін қолдана отырып алуға болады.

3- теорема. Егер $\left\{ x_{n} \right\}$ және $\left\{ y_{n} \right\}$ , ${\ y}_{n}$ ≠ 0, тізбектері жинақталатын болып, сонымен бірге, $\lim_{n \rightarrow \infty}y_{n}$ ≠ 0 болса, онда $\left\{ \frac{x_{n}}{y_{n}} \right\}$ тізбегі жинақталатын тізбек болады да $\lim_{n \rightarrow \infty}\frac{x_{n}}{y_{n}}$ = $\ \frac{\lim_{n \rightarrow \infty}x_{n}}{\lim_{n \rightarrow \infty}y_{n}}$ теңдігі орындалады. Алдын ала мына лемманы дәлелдейік.

Лемма. Егер $\left\{ y_{n} \right\}$ тізбегі ( ${\ y}_{n}$ ≠ 0) жинақталатын болып, сонымен бірге, $\lim_{n \rightarrow \infty}y_{n}$ ≠ 0 болса, онда $n_{0}$ нөмірі табылып, барлық $n\$ ˃ ${\ n}_{0}$ нөмірлері үшін $\left\{ \frac{1}{y_{n}} \right\}$ тізбегі шенделген тізбек болады.

Дәлелдеуі. Анықтама бойынша

$\underset{n \rightarrow \infty}{\ \ lim}y_{n} = b\$ ⇔ ∀ԑ > 0 ∃ ${\ n}_{0}⃒\ n\ ˃{\ n}_{0} \Rightarrow \left {\ y}_{n} - b \right = \left b - {\ y}_{n} \right < ԑ$ .

Енді ԑ $= \frac{b}{2}$ деп алып, айырма модулінің қасиетін пайдаланып, алдыңғы теңсіздікті мына түрде жазайық: $\frac{b}{2}$ > $\left b - {\ y}_{n} \right$ ≥ $b$ - $\left y_{n} \right$ , $n\$ ˃ ${\ n}_{0}$ . Бұдан $\left y_{n} \right$ > $\frac{b}{2}$ теңсіздігі шығады, ал шарт бойынша ${\ y}_{n}$ ≠ 0 болғандықтан, барлық ( $n\$ ˃ ${\ n}_{0}$ ) нөмірлері үшін $\frac{1}{y_{n}}$ < $\frac{b}{2}$ теңсіздігі орындалады.

3- теореманы дәлелдеуге көшейік. $\lim_{n \rightarrow \infty}x_{n}$ = $a, \ \underset{n \rightarrow \infty}{\ \ lim}y_{n} = b$ деп алайық. Теореманы дәлелдеу үшін (6-п, 1- теорема бойынша) $\ \frac{x_{n}}{y_{n}}$ - $\frac{2}{b}$ айырымы ақырсыз кіші екенін дәлелдеу жеткілікті. Бізге мына теғдіктер белгілі:

$\lim_{n \rightarrow \infty}x_{n}$ = $a \Leftrightarrow$ ${\ x}_{n} = a$ + $\alpha_{n}$ , $\lim_{n \rightarrow \infty}\alpha_{n}$ = $0$ ;

$\underset{n \rightarrow \infty}{\ \ \ lim}y_{n} = b$ ⇔ ${\ y}_{n} =$ b + $\beta_{n}$ , $\lim_{n \rightarrow \infty}\beta_{n}$ = $0$ .

Осыларды пайдаланып табатынымыз:

---

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс