Кванттық механикадағы физикалық шамалардың операторлары және орта мәндері


ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ және ҒЫЛЫМ МИНИСТРЛІГІ СЕМЕЙ қаласының ШӘКӘРІМ атындағы МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ
Инженерлік-технологиялық факультет
(факультеттің атауы)
«Техникалық физика и жылуэнергетика» кафедрасы
(кафедраның атауы)
СӨЖ
(жұмыстың аты)
Физикалық шамалардың орта мәндері.
(жұмыстың тақырыбы)
Орындаған: Ризабек Л. Ж.
Тобы: ТФ-701
Тексерген: Нурабаева Г. У.
Семей 2020
Мазмұны
Кіріспе3
1 Физикалық шамалардың операторлары. Операторлардың сызықтылығы және эрмиттілігі. 4
2 Де Бройл толқындарының кейбір қасиеттері. Физикалық шамалардың операторлары7
Қорытынды10
Пайдаланылған әдебиеттер тізімі11
Кіріспе
Атомдық деңгейдегі бөлшектердің қозғалысы мен əсерлесулерінің жалпы заңдылықтарын зерттейді жəне осы заңдылықтарға сүйене отырып атом ядросының, атомның, молекулалар мен қатты денелердің құрылысы теориялары мен қасиеттерін тағайындайды.
Классикалық физиканың атомдардың қасиеттері мен құрылысын жəне олардың жарықпен əсерлесуін түсіндіре алмауына байланысты физиканың жаңа бөлігі-кванттық механика пайда болды.
Кванттық механика, физиканың басқа да бөліктері сияқты, нақты физикалық құбылыстарды математикалық кескіндер (өрнектер, қатынастар) түрінде сипаттайды. Бұл кескіндер негізгі математикалық объектілерден: функциялардан, матрицалардан, операторлардан жəне олардың арасындағы қатынастардан құралады. Осы математикалық образдар мен физикалық объектілер - электрондар, атомдар жəне молекулалар арасындағы сəйкестік негізгі физикалық ұғымдар арқылы тағайындалады. Бір жағынан, бұл физикалық ұғымдар математикалық заңдылықтар мен əдістерді пайдалануға болатын математикалық объектілермен сипатталуы қажет, ал екінші жағынан, физикалық кұбылыстың мазмұны осы физикалық үғымдар арқылы сипатталатын физикалық құбылыстар мен тəжірибелерді қарастыру нəтижесінде тағайындалады.
1 Физикалық шамалардың операторлары. Операторлардың сызықтылығы және эрмиттілігі.
Оператор - бір толқындық функцияны басқа функцияға ауыстыратын математикалық символ, яғни кез келген әрекет. Операторды бүркеншігі бар әріппен белгілейді. Мысалы:
Бұл теңдіктегі
Кванттық механикада пайдаланылатын операторлардың тобы шектелген, себебі, кванттық механика суперпозиция принципіне
негізделген. Бұл принципті бұзба
 с үшін, операторлар сызықтық түрде болу керек. Сызықтық операторлардың математикалық анықтамасын келтіруге болады:
с үшін, операторлар сызықтық түрде болу керек. Сызықтық операторлардың математикалық анықтамасын келтіруге болады:
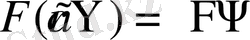 ;
;
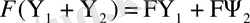 . (1. 2)
. (1. 2)
Бұл екі шартты біріктіруге болады:
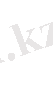
мұндағы
Физикалық шамалардың операторлары сызықтық ғана емес, өзіне түйіндес болу керек. (5. 1) қатысты мына түрде жазуға болады:
Бұл операторлық қатыстағы F тұрақты шама, оның кейбір мәндері (1. 3) -ті қанағаттандырады, олар
(1. 3а) қатысты сол жағынан
 .
.
Бұл қатысты
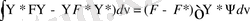 .
.
Нормалау шарты (3. 4) -ті және
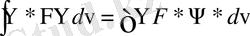 .
(1. 4)
.
(1. 4)
Бұл теңдік келесі теңдіктің дербес жағдайы болады:
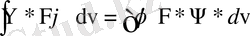 .
(1. 5)
.
(1. 5)
Сонымен, біз операторлардың өзіне түйіндес шартын алдық. (5. 5) теңдікті мына түрде жазуға болады:
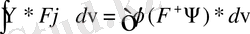 .
(1. 5a)
.
(1. 5a)
(1. 5) және (1. 5а) - ны салыстыра отырып, операторлардың өзіне түйіндес болу шартын қысқаша түрде көрсетейік:
мұндағы «+» символын эрмиттік түйіндес амалы ретінде түсіну керек,
яғни оны (1. 5) теңдіктің сол жағындағы интегралдың оң жағындағы интегралға ауысуы деп қарастырамыз.
Енді бастапқы
мұндағы ~ (тильда) белгісі
Бұл теңдік
2 Де Бройл толқындарының кейбір қасиеттері. Физикалық шамалардың операторлары
Француз ғалымы Луи де Бройль жарықтың корпускулалық-толқындық табиғаты жөніндегі түсініктерді дамыта келе, корпускулалық-толқындық дуализм тек оптикалық құбылыстарға тән ерекшелік емес, ол барлық микродүние физикасында жан-жақты қолданылуға тиіс деген батыл жорамал ұсынды. Бөлшектердің корпускулалық және толқындық қасиеттерін сипаттайтын шамаларды байланыстыратын математикалық өрнектер дәл фотондардікі сияқты. Сонымен қозғалыстағы кез келген бөлшекпен бір толқындық процесс байланысқан болады.
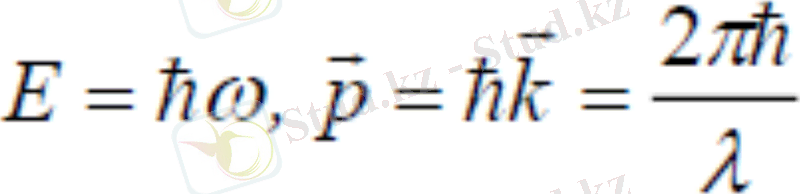
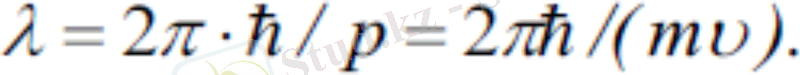
Келесі қатынас, де-Бройльша, зат бөлшектеріне салыстырылатын жазық монохромат толқын ұзындығын береді:
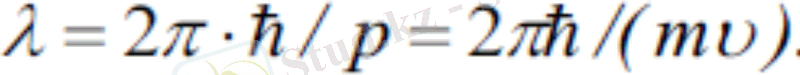 Бұл
де-Бройль толқын ұзындығы
Бұл
де-Бройль толқын ұзындығы
Тыныштық массасы нөл емес бөлшектер үшін p=mv өрнектері де-Бройль теңдеулері деп аталады
Де Бройль толқын ұзындығын энергияның функциясы ретінде табалық. Егер
U
потенциалдар айырмасы әсерінен электрон v жылдамдыққа ие болса, онда оның p импульсы
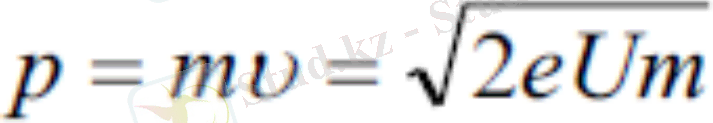
Осы электронмен де Бройль толқыны байланысқан, оның толқын ұзындығы
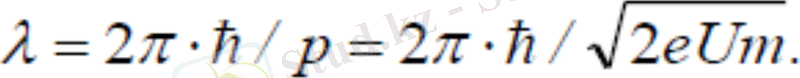
Оператор-шартты белгі, немесе ереже; оны қолдану арқылы бір функциядан басқа функцияны алуға болады. Физикада операторлар әдетте үстіне ˆ таңбасын қойып белгіленеді:
. L ˆ, B ˆ, A ˆ
Егер
L ˆ
операторы арқылы ψ
(х)
функциядан φ
(х)
функция алынатын болса, онда
Lˆ
операторы ψ
(х)
функциясына әсер етеді (немесе
Lˆ
операторы ψ
(х)
функциясын φ
(х)
-ға айналдырады) д. а. Оператордың осы амалы (әрекеті) былай жазылады:
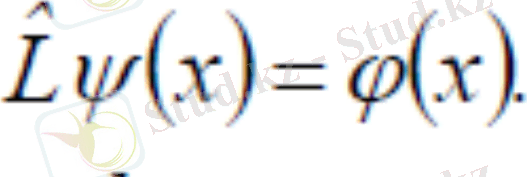
Кванттық механикада күйлердің суперпозиция принципі қанғат-тандырылуы үшін тек сызықтық операторлар қолданылады. Және кез келген сызықтық оператор емес, тек өзара түйіндес, немесе эрмиттік операторлар қолданылады.
Физикалық шамалардың операторлары . Кез келген физикалық шамаға (динамикалық айнымалыға) сәйкес оператор өзара түйіндес, эрмиттік болуға тиіс. Оператордың нақты түрі, оның көмегімен алынатын нәтиже тәжірибеге үйлесетіндей, таңдалып алынады. xˆ координат және x рˆ импульс проекциясының операторлары кванттық механиканың негізгі операторлары болып табылады. х координатының операторы ретінде осы координатқа көбейту операторын алу керек, яғни xˆ координат операторын қайсыбір f(x) функцияға қолдану, осы функцияны х - қа көбейтуге саяды :
xˆ f(x) = хf(x) . Сонымен, xˆ = х . Осылай болғандықтан координаттың орташа мәні формуласына сәйкес былай анықталады:
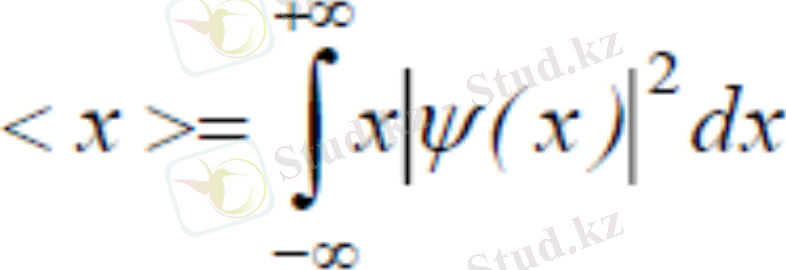
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz