Аспан жұлдыздарының аспан сферасына проекциялануы

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 67 бет
Таңдаулыға:

МАЗМҰНЫ

МАЗМҰНЫ: Кіріспе . . .

: 4

МАЗМҰНЫ: 1.

: 9 - СЫНЫПТАҒЫ АСТРОНОМИЯ САБАҚТАРЫНДА ӨТІЛЕТІН ТАҚЫРЫПТАРДЫ ТАЛДАУ

МАЗМҰНЫ: 1. 1

: Жұлдызды аспан. Аспан сферасы. Аспан координаталарының жүйелері . . .

МАЗМҰНЫ: 1. 2

: Жұлдызды аспанның жылжымалы картасы. Әр түрлі географиялық еңдіктегі аспан сферасының қозғалысы . . .

МАЗМҰНЫ: 1. 3

: Жергілікті, белдеулік және бүкіләлемдік уақыт. Астрономиядағы қашықтықты анықтаудың кейбір тәсілдері . . .

МАЗМҰНЫ: 2

: ЖАРАТЫЛЫСТАНУ - МАТЕМАТИКА БАҒЫТЫНДАҒЫ ОРТА МЕКТЕПТІҢ 11 - СЫНЫБЫНДА АСТРОНОМИЯДАН САБАҚ ТАҚЫРЫПТАРЫ

МАЗМҰНЫ: 2. 1

: Жұлдызды аспан және жұлдыздарға қарап бағдар алудың негізгі принципі. Жұлдыздар әлемі. Айнымалы жұлдыздар. Күн - Жер байланысы . . .

МАЗМҰНЫ: 2. 2

: Жер тобының планеталары. Алып - планеталар. Күн жүйесінің кіші денелері. Біздің Галактика. Басқа Галактикалардың ашылуы. Квазарлар . . .

МАЗМҰНЫ: 2. 3

: Әлем. Үлкен жарылыс. Әлем эволюциясының негізгі кезеңдері. Әлемнің кеңеюі. Әлемнің модельдері. Әлемдегі тіршілік және сана. Ғарышты игеру және адамзаттың оны игеру болашағы . . .

МАЗМҰНЫ: 3

: АСТРОНОМИЯ САБАҚТАРЫНДА АҚПАРАТТЫҚ ТЕХНОЛОГИЯЛАРДЫ ПАЙДАЛАНУ

МАЗМҰНЫ: 3. 1

: Астрономия сабағында жаңа технологияларды пайдалану әдістемесі. Астрономия және физика сабағын ақпараттық технологиялар негізінде жүргізу . . .

МАЗМҰНЫ: 3. 2

: Электронды оқулық - қазіргі кездегі білім берудің негізгі құрамдас бөлігі . . .

МАЗМҰНЫ: 3. 3

: 9 және 11 сыныптардағы астрономиядан сабақ жоспары . . .

МАЗМҰНЫ: Қорытынды . . .

: 68

МАЗМҰНЫ: Әдебиеттер тізімі . . .

: 69

МАЗМҰНЫ:

Кіріспе

Оқу процесіне жаңа информациялық технологияларды енгізу ісі астрономиямен тығыз байланыста өткізіледі, сондықтан физик мұғалімдер компьютерлік техниканы меңгеріп қана қоймай, оны өз пәндерінде кеңінен қолдануы тиіс. Осындай сәттерде физика және астрономия курсының мазмұнын да қайта қарап, оның компьютерлік сүйемелдеуде пайдалануға болатын бөлімдерін саралап, сабақтарды жаңалап өткізу әдістемелерін кұрастыру кажет. Жаңа технологияларды физикада пайдалану ісі бұрынғы белгілі әдістемелермен қатар педагогикалық жаңа технологияларды қолдануды талап етеді. Астрономиядан сабақ беру әдістемесі педагогикалық ғылымдар жүйесінің бір бөлігі болып табылады, пән ерекшелігіне қарай физика және астрономия курсын толығынан компьтерлік негізге ауыстыруға болмайды. Тек кейбір тақырыптар мен тарауларды оқып үйренуді ғана компьютерлік технологияға жүктеу керек.

Жұмыстың өзектілігі : Ғылым мен техниканың қарқынды даму кезеңінде астрономияны оқып үйрену өте маңызды мәселелердің бірі. Сондықтан астрономия тақырыптарын ақпараттық техногияларды қолдана отырып сабақ жүргізу оқушылар үшін өте тиімді.

Дипломдық жұмыстың мақсаты мен міндеттері: Aстрономиялық құбылыстарды оқушыларға түсіндірудің бір қиыншылығы - олар тек түнде жұлдыздар әлімінің аз ғана бөлігі көзге көрінеді, бірақ жердің күнді айнала қозғалыс себебінен аспан әлемін толық байқау қиындық тудырады. Бұл жұмыс осы тақырыпты кеңінен, әрі тиянақты талдау арқылы әдістемелік тұрғыдан егжей-тегжейлі қарастырылған.

Дипломдық жұмыстың зерттеу объектісі: Орта мектептің физика және астрономия сабақтарында астрономия тақырыптарын оқыту. Астрономиялық құбылыстарды қарапайым талдаудан бастап, галактикалар және әлемнің дамуындағы астрофизикалық құбылыстарын түсіндіру арқылы оқыту қарастырылған. Дипломдық жұмыста ақпараттық технологияларды пайдалана отырып 9 және 11 - сыныптың негізігі тақырыптарын оқыту әдістері қарастырылған.

Дипломдық жұмыстың ғылыми-әдістемелік жаңалығы: Әдістемелік тұрғыдан аз зерттелген орта мектептің астрономия сабақтары тақырыптарының әдістемесін жасау.

Жұмыстың құрылымы: Дипломдық жұмыс кіріспе, үш тарау, қорытынды және пайдаланылған әдебиеттер тізімінен құрылған.

9 - СЫНЫПТАҒЫ АСТРОНОМИЯ САБАҚТАРЫНДА ӨТІЛЕТІН ТАҚЫРЫПТАРДЫ ТАЛДАУЖұлдызды аспан

Айсыз ашық түні аспаннан сан жетпес жұлдыздар жымыңдап, адамның көңілін өздеріне еріксіз аударады. Шынында да, жер бетінің кез келген орнынан бір мезетте аспан күмбезінен құралсыз көзбен үш мыңға тарта жұлдызды көруге болады. Оларды танып - білмек үшін адамдар өте ерте заманда жұлдыздардың өзара орналасуын жан - жануарларға немесе басқа нәрселерге ұқсатып топтастырып, оларға шоқжұлдыз атауларын берген. Мысалы, Геркулес пішіні бір тізесін бүккен адамға, Торпақ - бұқаның мүйізіне, Аққу мен Бүркіт - қанатын жая самғап ұшқан құстарға ұқсайды. Сондай-ақ Қарақұрт, Жылан, Сужылан т. б. шоқжұлдыздарының атаулары олардың бейнелерінің өздері аттас жәндіктерге айна-қатесіз ұқсауынан туындаған. Сонымен қатар қайсыбір шоқжұлдыз атауларының мағыналық мәні де бар. Мысалы, Таразы шоқжұлдызының атауы күзгі күн мен түннің теңелуі кезінде Күннің осы шоқжұлдызда (осыдан 2000 жыл бұрын) орналасуынан туған. Сондай-ақ шоқжұлдыз атаулары қатарында аңыздарда кездесетін кейіпкерлер мен жануарлар да баршылық. Мысалы, Персей, Қауыс-Мерген, Айдаһар, Кентавр т. б.

Қайсыбір шоқжұлдыздардың атауы ата - бабаларымыздың тұрмыс - салт әдет - ғұрып, ғарыштану және діни түсніктермен байланыстырылған. Астрономия тарихын зерттеуші орыс ғалымы Д. О. Святский өз еңбектерінде дала қазақтарының Темірқазық пен оның маңындағы бірнеше жұлдыздарды аспан қазығына арқандалған жылқы ретінде бейнелейтінін жазған (1. 1-сурет)

Сурет 1. 1 - Кіші Аю мен Үлкен Аю жылқы пішінінде бейнеленген

Шоқжұлдыздардың астрономияда осы күндері қолданып жүрген атауларының 48-і өте ертеден, Ежелгі Мысыр, Вавилон және Грекия замандарынан белгілі. Ежелгі грек астрономдары Гиппарх (б. з. д. 180 не 190-125 жж. ) Птолемей (90-160 жж. ) шоқжұлдыз атауларын бір жүйеге келтіріп, олардағы жұлдыздардың алғашқы тізімдерін, суреттемесін жасаған. Бірақ ол тізімде Жер шарының солтүстік жартышарында орналасқан елді мекендердің аспанында көрінетін шоқжұлдыздар ғана қамтылған. Ал аспанның қалған бөліктерінің жұлдыздарын саяхатшылар XVI-XVIII ғасырларда оңтүстікке шеккен сапарларында шоқжұлдыздарға топтастырып, картаға түсірген.

Шоқжұлдыз дегеніміз - аспанның нақты шекарасы анықталған белгілі бір бөлігі.

Аспанда барлығы 88 шоқжұлдыз белгіленген. Шоқжұлдыз шекараларылары Халықаралық астрономия одағының (ХАО) арнаулы қаулысы бойынша бекітілген, бipaқ олардың ешқандай физикалық мағынасы жоқ. Шоқжұлдыздардың 31-i аспанның солтүстік жартышарында, 48-i оңтүстік жартышарында, ал қалған 9-ы аспан экваторының бойында eкі жартышарға да ортақ орналасқан. Халықаралық деңгейде шоқжұлдыз атаулары латын тілінде қолданылады. Мысалы, бізге қазақ халық астрономиясынан жақсы таныс Жетіқарақшының астрономиялық аталуы - Үлкен Аю. Сол сияқты Ұшқар-Таразы - Орион, Қамбар - Арыстан, Қарақұрт - Кассиопея деп аталады.

Жарық жұлдыздардың көпшілігінің ежелден келе жатқан өзіндік атаулары бар. Олар, әдетте, жұлдыздардың өзіндік ерекшеліктерін сипаттайды: Сириус - “жарқырауық”, Альдебаран - “iз басушы” немесе шоқжұлдыз бейнеленетін зат бөліктері мен жануарлар мүшелерінің атауымен байланыстырылады. Мысалы, Жетқарақшының жеті жұлдызының төртеyi Хорезмдік ұлы астроном Бирунидің "Канон Масуди” атты еңбегінде аю денесіне қатысты Мерак (β) - “қарын”, Фахз (γ) - “сан, бөксе”, Маграз (δ) - “құйрық басы”, Мизар (ξ) - “ортасы” деген мағынада таңбаланған. Бируни өзінен шамамен мың жыл бұрын өмір сүрген Птолемейдің жүйелеген жұлдыз атауларын араб тіліне аударып, сәл ғана өзгерткен. Қазіргі кезде қолданылып жүрген 300-ге тарта жұлдыздың төл атауларының 15%-ы грек, 5%-ы латын, 80%-ы араб тілінде айтылады.

Түнгі аспанға қарағанымызда, жұлдыздардың жарықтылықтары әр түрлі екенін аңғарамыз. Сириус, Арктур және Вега жарқырап көзге бірден түссе, Алькордың көмескі жұлдыз екенін байқаймыз. Жұлдыздардың көзге көрінерлік жарықтылығын санмен өрнектеу үшін астрономдар көрінерлік жұлдыздық шама деген ұғымды пайдаланады. Мұны алғаш ежелгі грек астрономы Гиппарх еңгізген. Ол аспандағы көзге көрінетін жұлдыздарды алты топқа бөліп, ең жарық жұлдыздарды бірінші жұлдыздық шамаға, ал ең көмескілерін алтыншы жұлдыздық шамаға тағайындады.

XIX ғасырдың ортасында ағылшын астрономы Норман Погсон жұлдыздық шаманың осы замағы шкаласын ұсынды. Бұл шкалада 5 жұлдыздық шама (ж. ш. ) жұлдыз жарықтылығының 100 есе өзгеруін көрсетеді. Демек, бip ж. ш. айырмашылығы жұлдыз жарықтылығының есе өзгеруіне сәйкес болады.

Көрінерлік ж. ш. т (лат. magnitudo - “шама” сөзінен) әрпімен таңбаланады. Астрономияда жұлдыз жалтырлығы (жылтырауы) деген ұғым қолданылады. Ол жұлдыздың одан келетін сәулеге перпендикуляр орналасқан бірлік ауданды жарықтандыратын жарық мөлшерін береді.

Жарық өлшегіш аспап фотометрді пайдаланып жүргізілген өте дәл өлшеулер жұлдыз жалтырлығының әрқилы болатынын көрсетеді. Сондықтан кейбір жұлдыздардың жалтырлығы ж. ш. бойынша бөлшек және теріс мәндермен де өрнектеледі.

Аспандағы ең жарық жұлдыз Сүмбіленің (Сириус) көрінерлік ж. ш. - сы m = -1, 58; Күннің ж. ш. -сы m = -26, 6; толған Айдың ж. ш. -сы m = -12, 7.

Бір жұлдыздың жалтырлығы жоғары, ал енді біреуінің төмен болуы жұлдыздың шын мәніндегі жарықтылығы туралы мәлімет бере алмайды. Себебі жарық жұлдыздың бізге жақын орналасуынан көрінерлік ж. ш. - сы жоғары болуы мүмкін, бірақ тура осындай жұлдыздың алысырақ орналасуынан көрінерлік ж. ш. - сы төмен болады.

Жұлдыздардың шын мәніндегі жарықтылығын анықтау үшін абсолют жұлдыздың шама түсінігі қолданылады. М - абсолют ж. ш., жұлдыздың стандарт қашықтық - 10 парсек немесе 32, 6 жарық жылы қашықтығында орналасқандағы көрінерлік ж. ш.

Мұндай қашықтықта абсолюттік ж. ш. аспандағы ең жарық жұлдыз Сириус үшін +1, 41, Күн үшін +4, 8, ал Бетельгейзе үшін -6, 0, Ригель үшін -7, 0 болар еді (1. 1-кесте) .

Кесте 1. 1 - Жарық жұлдыздар тізімі

Қысқаша белгіленуі: Қысқаша белгіленуі

Тура көтерілуі, А: Тура көтерілуі, А

Еңістігі,δ:

Еңістігі,

Көрінерлік жұлдыздық шамасы, m: Көрінерлік жұлдыздық шамасы, m

Абсолютжұлдыздық шама:

Абсолют

жұлдыздық шама

: 1

Қысқаша белгіленуі: 2

Тура көтерілуі, А: 3

Еңістігі,δ: 4

Көрінерлік жұлдыздық шамасы, m: 5

Абсолютжұлдыздық шама: 6

: Сириус

Қысқаша белгіленуі: αСМа

Тура көтерілуі, А: 6 caғ 45 мин

Еңістігі,δ: -16" 43'

Көрінерлік жұлдыздық шамасы, m: -1, 58

Абсолютжұлдыздық шама: +1, 41

: Арктур

Қысқаша белгіленуі: α Boo

Тура көтерілуі, А: 14caғ 16 мин

Еңістігі,δ: +19" 11'

Көрінерлік жұлдыздық шамасы, m: -0, 05

Абсолютжұлдыздық шама: -0, 2

: Вега

Қысқаша белгіленуі: α Lyr

Тура көтерілуі, А: 18 caғ 37 мин

Еңістігі,δ: +38° 47'

Көрінерлік жұлдыздық шамасы, m: 0, 03

Абсолютжұлдыздық шама: +0, 5

: Капелла

Қысқаша белгіленуі: α Aur

Тура көтерілуі, А: 5 caғ 17 мин

Еңістігі,δ: +46° 00'

Көрінерлік жұлдыздық шамасы, m: 0, 08

Абсолютжұлдыздық шама: -0, 6

: Ригель

Қысқаша белгіленуі: β Ori

Тура көтерілуі, А: 5 caғ 15 мин

Еңістігі,δ: -8° 12'

Көрінерлік жұлдыздық шамасы, m: 0, 12

Абсолютжұлдыздық шама: -7, 0

: Процион

Қысқаша белгіленуі: α CMi

Тура көтерілуі, А: 7 caғ 39 мин

Еңістігі,δ: +5° 14'

Көрінерлік жұлдыздық шамасы, m: 0, 37

Абсолютжұлдыздық шама: +2, 65

: Бетельгейзе

Қысқаша белгіленуі: α Ori

Тура көтерілуі, А: 5 caғ 52 мин

Еңістігі,δ: +7° 24'

Көрінерлік жұлдыздық шамасы, m: 0, 42

Абсолютжұлдыздық шама: -6, 0

: Альтаир

Қысқаша белгіленуі: α Agl

Тура көтерілуі, А: 19 caғ 51 мин

Еңістігі,δ: +8° 52'

Көрінерлік жұлдыздық шамасы, m: 0, 77

Абсолютжұлдыздық шама: +2, 3

: Альдебаран

Қысқаша белгіленуі: α Tau

Тура көтерілуі, А: 4 caғ 36 мин

Еңістігі,δ: +16° 31'

Көрінерлік жұлдыздық шамасы, m: 0, 85

Абсолютжұлдыздық шама: -0, 7

: Альголь

Қысқаша белгіленуі: δ Per

Тура көтерілуі, А: 3 caғ 08 мин

Еңістігі,δ: +40° 57'

Көрінерлік жұлдыздық шамасы, m: 1, 12

Абсолютжұлдыздық шама: -0, 3

: Регул

Қысқаша белгіленуі: α Leo

Тура көтерілуі, А: 10 сағ 08 мин

Еңістігі,δ: +11° 58'

Көрінерлік жұлдыздық шамасы, m: 1, 35

Абсолютжұлдыздық шама: -0, 6

: Кастор

Қысқаша белгіленуі: α Gem

Тура көтерілуі, А: 7 caғ З5 мин

Еңістігі,δ: -26 °19'

Көрінерлік жұлдыздық шамасы, m: 1, 58

Абсолютжұлдыздық шама: +0, 85

: Темірқазық

Қысқаша белгіленуі: α Umi

Тура көтерілуі, А: 1 caғ. 49 мин

Еңістігі,δ: +89 °02'

Көрінерлік жұлдыздық шамасы, m: 2, 02

Абсолютжұлдыздық шама: -4, 6

Аспан сферасы

Жұлдыздардың, планеталардың, т. б. аспан денелерінің орналасу орындарын анықтау және өлшеу сияқты практикалық мәселелерді шешу үшін астрономияда аспан сферасы деген ұғым қолданылады.

Аспан сферасы - радиусы анықталмаған жорамал сфера. Аспан шырақтары әр түрлі қашықтықта болғандықтан, сфераның бетіне бақылаушы белгілі бір уақытта өзі орналасқан орыннан көретін бүкіл аспан шырақтары проекцияланады (1. 2-сурет) .

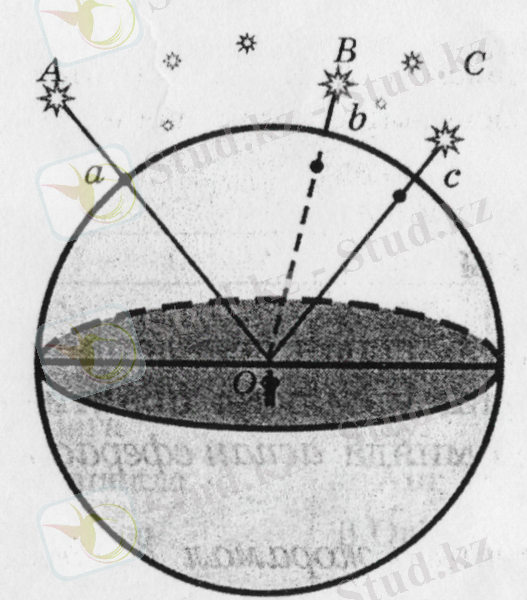
Сурет 1. 2 - Аспан жұлдыздарының аспан сферасына проекциялануы

Аспан сферасының орталық нүктесі, әдетте, Жер центрі немесе жер бетіндегі бақылаушы тұрған орынмен сәйкестендіріледі.

Аспан сферасында тек бұрыштық өлшеулер ғана қарастырылады. Бұрыштық қашықтық деп сферадағы екі нүктенің арасындағы доғамен өлшенетін қашықтықты немесе оған сәйкес орталық бұрыш шамасын айтады. Яғни, бұл - бақылаушы көзімен қарағандағы (аспан сферасының орталық нүктесінен) осы екі нүктеге тарайтын сәулелердің арасындағы бұрыш. Аспан сферасы туралы ұғым адамзат тарихында өте ертеде пайда болған. Себебі аспан адамға жер бетін көмкерген өте үлкен күмбез тәрізді болып көрінеді. Ежелгі дүниетаным бойынша бүкіл әлем бетінде козғалмайтын шырақтар (Ай, Күн, планеталар, жұлдыздар) орналасқан мөлдір сфералардан құралған. "Аспан" сөзінің өзі көне үнді тілінде "тастан жасалған күмбез" деген ұғымды білдіреді. Түркі халықтарының ежелгі ұғымы бойынша аспан (көк) жеті немесе тоғыз қабаттан тұрады. Оларда дәрежелеріне сәйкес тәңірлер мекендейді. Астрономияның дамуы мұндай түсініктің қате екенін дәлелдеп берді, әйтсе де ыңғайлы болғандықтан, аспан сферасы деген ұғым қазіргі астрономияда кеңінен қолданылады.

Ерте заманда аспан сферасы айналады деп есептелсе, біз оның айналысы Жердің өз осін айналуынан пайда болатын көрінерлік құбылыс екенін жақсы білеміз. Жер шары батыстан шығысқа карай айналатындықтан, аспан бізге шығыстан батысқа қарай айналатын болып көрінеді. Осыдан аспан шырақтарының шығыстан туып, батыстан батуы туындайды.

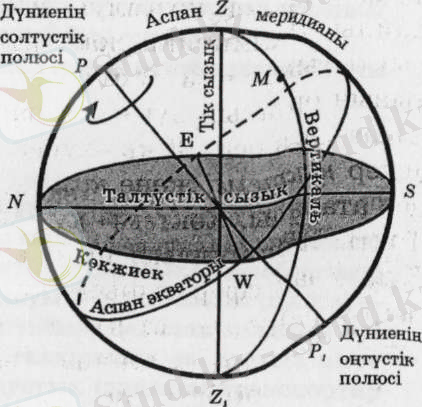
Аспан сферасының негізгі элементтері 1. 3-суретте көрсетілген.

Зенит

Надир

Сурет 1. 3 - Аспан сферасының элементтері

Зенит (Z) нүктесі бақылаушының дәл төбесінде, ал Надир (Z ₁ ) - сфераның қарама-қарсы нүктесінде орналасқан. Осы екі нүктені қосатын түзу вертикаль сызық немесе тік сызық, оған перпендикуляр әрі аспан сферасының нүктесі арқылы өтетін жазықтық математикалық немесе нақты көкжиек жазықтығы деп аталады. Ол аспан сферасын қиып, үлкен дөңгелек көкжиек түзеді. Көкжиек аспан сферасын көрінетін және көрінбейтін екі бөлікке бөледі. Зениттен М шырақ арқылы надирге дейін өтетін өтетін үлкен дөңгелек шырақ вертикалі деп аталады. Аспан сферасы және шырақтардың тәуліктік айналысы дүние осінің төңірегінде өтеді. Жер өлшемі жұлдыздарға дейінгі қашықтықпен салыстырғанда өте кіші болғандықтан, іс жүзінде дүние осі жер бетіндегі кез келген орын үшін Жер осіне параллель болады. Дүние осінің аспан сферасымен қиылысатын нүктелері аспан сферасының айналысына қатыспайды. Сондықтан да олар дүние полюстері деп аталады. Төңірегінде аспан сферасының айналысы

сағат тілінің айналу бағытына кері болатын полюс дүниенің солтүстік полюсі қарсы полюс дүниенің оңтүстік полюсі деп аталады. Дүниенің солтүстік полюсі маңында (1 ⁰ -қа жуық қашықтықта) Темірқазық жұлдызы орналасқан.

Зенит және дүние осі арқылы өтетін жазықтық аспан меридианының жазықтығы, ал оның аспан сферасымен қиылысқан кезінде пайда болатын үлкен дөңгелек аспан меридианы болып табылады. Аспан меридианы аспанның тәуліктік айналысына қатыспайды да, көкжиекпен екі нүктеде қиылысады, олар - көкжиектің оңтүстік (S) және солтүстік (N) нүктелері. Математикалық көкжиек және аспан меридианы жазықтықтарының қиылысуында пайда болатын түзу талтүстік сызық деп аталады. Оның себебі тал түсте тігінен қойылған бағанның көлеңкесі осы түзу бойымен бағытталады. Жер бетінің кез келген нүктесінде нақты оңтүстік-солтүстік бағытты осы талтүстік сызық бағыты береді. Сондықтан ол Жер бетінде дұрыс бағдарлану үшін өте қажет бағыт болып табылады. Аспанда оның қызметін аспан меридианы атқарады.

Аспан сферасының орталық нүктесі арқылы өтетін және дүние осімен тік бұрыш жасайтын жазықтық аспан экваторының жазықтығы деп аталады. Жер экваторына параллель бағытталған бұл жазықтық пен аспан сферасымен қиылысқанда пайда болатын үлкен дөңгелек аспан экваторы деп аталады. Аспан экваторы аспан сферасын оңтүстік және солтүстік екі жартышарға бөледі және көкжиекпен екі нүктеде - шығыс (Е) және батыс (W) нүктелерінде қиылысады.

Дүние полюстері және шырақ арқылы өтетін үлкен дөңгелек шырақтың еңістік дөңгелегі деп аталады. Кез келген шырақ аспан сферасының тәуліктік айналысына қатыса отырып, тәуліктік параллель деп аталатын кіші дөңгелектер бойымен қозғалады. Бұл жайт жылжымайтындай етіп бекітілген фотоаппаратпен түсірілген түнгі аспанның суретінен айқын көрінеді.

Эклиптика - Күннің зодиак шоқжұлдыздары бойымен жылдық қозғалысы өтетін үлкен дөңгелек. Күннің эклиптика бойымен қозғалуы Жердің Күнді айналуынан туындайды. Эклиптика жазықтығы аспан экваторының жазықтығына ε= 23°26' бұрыш жасай орналасқан. Күн шарығының орталық нүктесі аспан экваторын жылына екі рет - 21 наурыз бен 23 қыркүйек маңында қиып өтеді. Бұл нүктелер көктемгі және күзгі күн мен түннің теңелу нүктелері деп аталады. Көктемгі күн мен түннің теңелу нүктесі (ϓ- Тоқты шоқжұлдызының таңбасымен белгіленеді) арқылы Күн аспан сферасының оңтүстік жартышарынан солтүстік жартышарына, ал күзгі күн мен түннің теңелу нүктесі(Ω-Таразы шоқжұлдызының таңбасымен белгіленеді) арқылы кері бағытта өтеді.

Күн мен түннің теңелу нүктелеріне 90° құрайтын Күннің тоқырау нүктелері орналасады. Жазғы күннің тоқырау нүктесі Торпақ пен Егіздер шоқжұлдыздарының шекарасында жатыр, ол Шаянның зодиак таңбасымен белгіленеді. Қысқы күннің тоқырау нүктесі Мерген шоқжұлдызында жатыр, ол Ешкімүйіздің (Ұғылақ) таңбасымен белгіленеді (1. 4-сурет) .

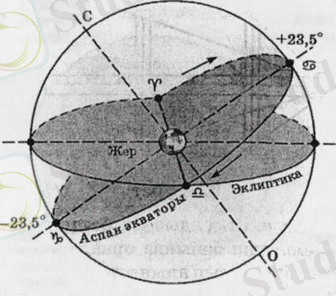
Сурет 1. 4 - Аспан сферасындағы эклиптика және экватордың орналасуы

Негізгі жазықтықтар мен үлкен дөңгелектер аспан координаталарын енгізуде қолданылады [1] .

Аспан координаталарының жүйелері

Жер бетіндегі кез келген нүктенің орны - ендік және бойлық (φ және λ) географиялық координаталардың көмегімен анықталатыны белгілі. Аспан координаталары аспан денелерінің аспан сферасында орналасуын анықтайды.

Аспан координаталары географиялық координаталарға ұқсас, бірақ астрономдар географтарға қарағанда әp түрлі зерттеу мәселелеріне байланысты аспан координаталарының бірнеше жүйесін қолданады. Солардың екеуімен танысайық.

Координаталардың көкжиектік жүйесі. Жұлдыздардың көкжиекке және дүние бұрыштарына қатысты көрінерлік орналасуын қарастырсақ, онда координаталардың көкжиектік жүйесін алу ыңғайлы. Бұл жүйедегі негізгі жазықтық - математикалық көкжиек жазықтығы. Аспан шырағының орны екі бұрышпен анықталады, оның бірі - көкжиек сызығы бойымен өлшенетін шырақ вертикаліне дейінгі бұрыш - азимут астрономияда, әдетте, оңтүстік нүктеден батысқа қарай, ал географияда солтүстік нүктеден шығысқа қарай есептелінеді. Екіншісі - вертикаль бойымен өлшенетін (1. 5-сурет) шырақтың көкжиектен бұрыштық қашықтығы - шырақ биіктігі(һ) .

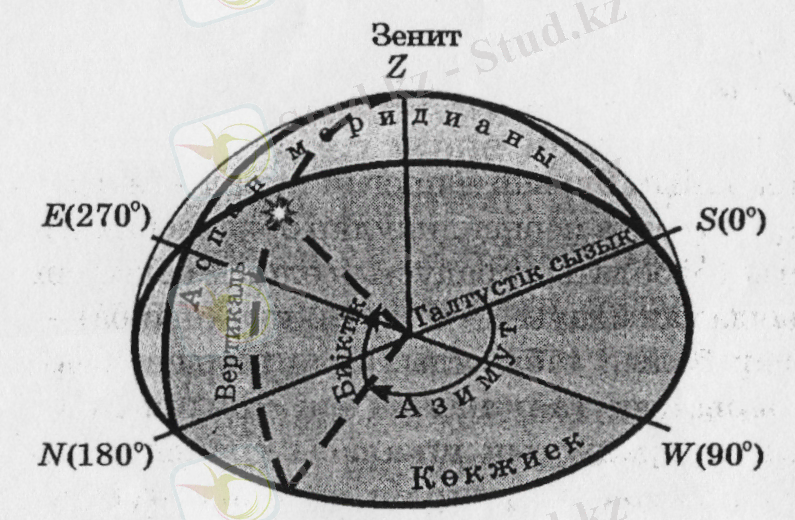
Сурет 1. 5 - Аспан сферасындағы координаталар жүйесі

Шырақ биіктігінің -90°-тан +90°-қа дейін болады. Бұрыш өлшегіш құрал көмегімен (мысал теодлоит) аспан денесінің жиектік координаталарын анықтау оп-оңай.

Бірақ бұл координаталар жүйесін қолдану кезінде туындайтын қолайсыз жағдайлар да бар. Себебі аспан денелерінің көкжиектік координаталарының мәні уақыт пен бақылаушының тұрған орнына байланысты. Көкжиектік координаталар шырақтардың аспанда белгілі бір орын мен уақыттағы орналасуын анықтайды.

Координаталардың экваторлық жүйесі. Аспан сферасының көрінерлік айналыста болатынын білдік, әрі жұлдыздардың ондағы орындары өзгермейді. Сондықтан онымен бірге қозғалатын координаталар жүйесін қолдану ыңғайлы. Ол - экваторлық координаталар жүйесі (1. 6-сурет) .

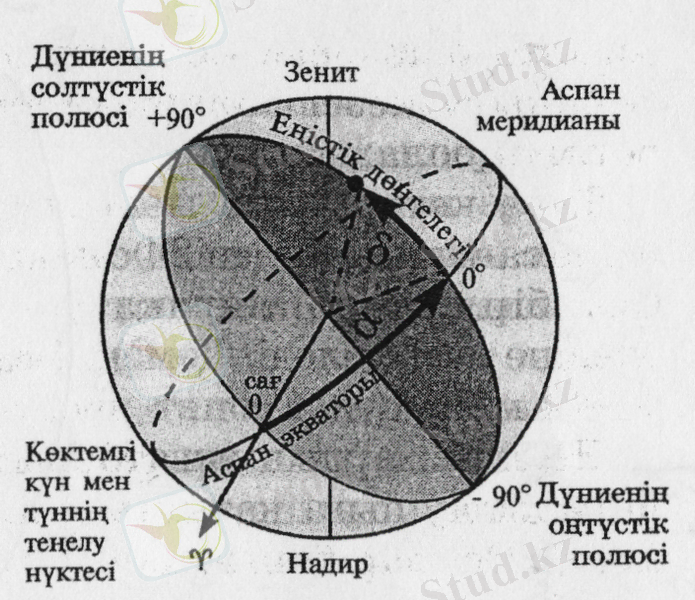
Сурет 1. 6 - Экваторлық координаталар жүйесі

Оның негізгі жазықтығы - аспан шырағының аспан экваторынан бұрыштық қашықтығын көрсететін координата еңістік деп аталады да, δ әрпімен белгіленеді. Ол еңістік дөңгелегі бойымен өлшенетін доға ұзындығына тең. Еңістіктің аспан сферасының солтүстік жартышарында таңбасы «оң», мәні 0 - ден +90 ⁰ - қа дейін, ал оңтүстік жартышарда «теріс», 0-ден -90 ⁰ - қа дейін.

Экваторлық жүйеде қолданылатын екінші координата географиялық бойлыққа ұқсас. Ол тура көтерілу деп аталада да, α әрпімен белгіленеді. Тура көтерілу координатасының мәні аспан экваторының бойымен көктемгі күн мен түннің теңелу нүктесінен шырақтың еңістің дөңгелегіне дейін аспан сферасының айналу бағытына қарама-қарсы бағытта өлшенеді. Сондықтан да жұлдыздардың көкжиектен шығу кезегі олардың тура көтерілу мәндерінің өсу ретімен болады.

Тура көтерілудің мәні градустық (0°-тан 360°-қа дейін) және сағаттық (0-ден 24 сағ-қа дейін) бірліктермен өлшенеді. Осы бірліктердің арақатынасын анықтау 24 сағ = 360° екеніне негізделеді. Демек, 1 сағ = 15°; 1 мин = 15'; 1 с = 15"; 1° = 4 мин; 1' = 4 с.

Жұлдыздардың экваторлық координаталарының мәндері бақылаушыға қатысты емес, әрі ұзақ уақыт бойы өзгермейді. Осылар бойынша олар аспан карталарында орналастырылады және каталогтарда тіркеледі.

1. 2 Жұлдызды аспанның жылжымалы картасы. Әр түрлі географиялық еңдіктегі аспан сферасының қозғалысы

Жұлдызды аспанның жылжымалы картасы (ЖАЖК) белгілі бір орында жылдың кез келген күні мен тәуліктің әр сәтінде жұлдызды аспанның көрінісін анықтау мақсатында қолданылады. ЖАЖК екі бөліктен құралған: жұлдыздар картасы және қондырма дөңгелек.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.