Комбинаторикалық есептерді шешудің негізгі тәсілдері

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 30 бет
Таңдаулыға:

МАЗМҰНЫ
Кіріспе
3
1Комбинаторика элементерінің түсінігі
1.1Комбинаторика ұғымы, шығу тарихы
4
1.2Комбинаториканыңнегізгі элементтері
5
2 Комбинаторика элементтерін пайдаланып есептер шығару
2.1Комбинаторикалық есептерді шешудің негізгі тәсілдері
10
2.2Қайталамалы таңдамалар үшін қолданылатын комбинаторика формулалары
14
2.3 Мультижиындар
22
3 Ньютон биномы
23
3.1 Паськал үшбұрышы
23
4 Комбинаторика элементтерін мектепте қолдану
28
5 Практикалық бөлім
30
Қортынды
32
Пайдаланылған әдебиеттер
33

Кіріспе

Курыстық жұмыстың өзектілігі:Комбинаторика - математика тарауларының бірі. Мұнда шекті жиын элементтерінің түрлі қосылыстары, басқаша айтқанда, әр қилы конфигурациялары (пішін үйлесім - ағылш. сonfiguration, белгілі бір жүйені, аппараттық жабдықтарды, оның нақты параметрлерін немесе сипатгамаларын, құрылғылар құрамын (бөліктерін), өзара байланыстарын анықтай отырып орналастыру). Қарастырылып, олардың сандары саналады және де есептеледі. Қазіргі кезде комбинаторика математика салаларының ішінде өте жедел дамып отырған бөлігіне айналды информация мен ықтималдықтар теорияларына кеңінен қолданылуы. Дискреттік деп аталып жүрген математиканың өзінде де көп ықпалын тигізетін міне, осы қосылыстар теориясы. Шешуі нешеу, неше тәсілмен деген сұрақтарға жауап беруді қажет ететін есептер - комбинаторикалық есептер деп аталады. Мұндай есептерді шешумен айналысатын математика саласы комбинаторика деп аталады
Комбинаторика элементтері тақырыбы алғаш мектептерде 1973-1975 жылдары факультативтік жұмыстарда жүзеге асты. Ал, 1975-1976 жылдары оқу жылынан бастап бұл, тақырып жалпыға міндетті жаңа бағдарлама бойынша оқытылды. Кейінірек, 1980 жылдан бастап математиканың бұл бөлімі мектеп бағдарламасынан алынып тасталды. Осылайша, ширек ғасырға жуық уақыт бойы орта мектепте де, педагогикалық жоғары оқу орындарында да комбинаторлық талдау есептерін шығару және оларды оқыту әдістемесі оқылмай қойды.
Қазіргі таңда комбинаторика кездейсоқ жағдайлар алгебрасы және статистика теорясы элементтері бастамалары республикамыздағы бірқатар авторлардың алгебра оқулықтарынан, сондай-ақ Қазақстанның жалпы орта білім беретін мектебінің 5-6 сыныптарына арналған математиканың жаңа стандарттық бағдарламаларының мазмұнынан нақты орын алды.
Орта мектептерде әзірге Ықтималдық теориясының бастамасы тақырыбын оқыту тәжірибесі жоқ сондықтан, Комбинаторика элементтері және оны ықтималдық теориясында қолдану курсының сипаттамасы қызығушылық тудыруы мүмкін.
Жұмыстың мақсаты: ықтималдықтар теориясы мен комбинаторика элементтерін теориялық тұрғыда негіздеп, комбинаторика элементтерін қолданып есептер шығару әдістемесін жетілдіру.
Жұмыстың міндеттері:
1.Комбинаторика әдісі туралы мәлімет жинау.
2. Комбинаторика қасиеттерін қарастыру.
3. Мектепте комбинаторика элементтерін оқытып-үйрету.
4.Курстық жұмысқа сәйкес есептерді шығру.
I Тарау.Комбинаторика элементтеріне түсінік

1.1 Комбинаторика ұғымы, шығу тарихы
Комбинаторика - дискретті объектілерді, жиындарды және олардың арасындағы қатынастарды зерттейтінматематиканыңбір бөлімі. Комбинаторика математиканың көп салаларымен - алгебрамен , геометриямен, ықтималдықтар теориясыментығыз байланысты және генетика, информатика, статистикалық физика салаларында кеңінен қолданылады. Комбинаторика терминін 1666 жылы Лейбниц енгізген. Комбинаторика(лат. сombino - жалғастырамын) комбинаторикалық анализ деп те аталады. Комбинаторикалық анализ комбинаторикалық математика, комбинаторика - математиканың кез келген шектеулі жиын (шектеудің кейбір шарттарын шексіз жиын) бөліктерінің орналастырылуы мен өзара орналасуына байланысты мәселелерін зерттейтін бөлімі.
Комбинаторикалық сипаттағы идеялар ықтималдық теориясы, алгебра тәрізді математикалық бөлімдерінде өте кең тараған. Комбинаторикалық анализ есептері ерте кезден-ақ белгілі болған. Оның дамуына көптеген математиктер елеулі үлес қосты. Бірақ, комбинаторикалық анализ өз алдына пән ретінде тек ХХ ғасырда ғана қалыптаса бастады. Комбиторикалық графтар теориясы, шектеулі автоматтар теориясы тәрізді математиканың салаларымен тығыз байланысты. Графтар теориясы (ағылш. graph theory) - түйіндері нүктелер жиыны, ал түйіндердің жалғасуы (қабырға деп аталатын) парлы екі нүкте болып келетін тор түрінде бейнеленеді. Егер, түйіндердің жалғасу реті айтарлықтай маңызды болса - бағытталған граф, әйтпесе бағытталмаған граф болады.
Оның тәжірибелері ғылыми тәжірибелерді жоспарлауды және оларға талдау жасауда, сызықтық және динамикалық бағдарламалауда, математикалық экономикада т.б. ғылым мен техникалық көптеген салаларында қолданылады. Комбинаторикалық анализ проблемасының үш түрі бар.
Санап шығу есептерінде объектілердің шектеулі жиынынды кездесетін шарттарды қанағаттандыратын орналастырулар саны қарастырады. Іс жүзінде мұндай есептер жасаушы функциялар әдісі мен Д.Пойаның (1887-1985) (американдық математик) санап шығу әдісінің көмегімен шешіледі.
Салу есептерінде кейбір қасиеттері сақталатын шектеулі жиын бөліктері конфигурациясының болуы, егер болса оның салынатындығы туралы мәселелер қарастырылады. Таңдап алу есептерінде ішкі жиын бөліктерінің кейбір құрамын таңдап алу шарттары зерттеледі.мұндай есептерді шешкенде комбинаторлық ойлармен қатар алгебралық аппарат та қолданылады.
Комбинаторикалық формулаларды қолдану кездейсоқ оқиғалардың ықтималдықтарын есептеуді біршама жеңілдетеді. Іс жүзінде адамға өзара орналасуының барлық мүмкін жағдайларын есептеуге немесе қандайда бір іс-әрекеттің барлық мүмкін нәтижелерін және оны орындауға қажетті барлық мүмкін тәсілдер санын есептеуге тура келеді. Мысалы, футболдан әлем біріншілігінде жартылай финалға шыққан 4 команда арасында алтын, күміс, және қола медальдары неше түрлі тәсілдермен иемделінеді және т.с.с. Бұл есептерде заттардың өзара орналасуының немесе іс-әрекеттің барлық мүмкін комбинациялары қарастырылады.
Сондықтан, мұндай есептерді комбинаторикалық есептер деп атайды. Комбинаторика есептерін шешуде қолданылатын өзіндік заңдылықтар мен формулалар бар. Кейбір комбинатроикалық есептермен ежелгі грек математиктері де айналысқан. Дегенмен, бұл саладағы маңызды нәтижелерді алгебра мен ықтималдықтар териясының дамуына байланысты ХVII және XVIII ғасыр математиктері ала бастаған. Алғашында ықтималдықтар теориясы, негізінен құмар ойындардың (ойын сүйегін тастау,карта ойындары және т.с.с) мұқтаждығынан туындаған. Мәселен, Людовик 14 тұсында құмар ойындардың шынайы әуесқойы Кавалер де Мере үш ойын сүйегін қатар тастау нәтижесінде қосындысына 12 ұпайдан гөрі 11 ұпайдың жиірек түсетінін байқаған. Бірақ, оның ойынша бұл ұпайлардың екеуін де әр түрлі 6 комбинациямен алуға болады деп санаған.
11 ұпай үшін: 6,4,1,6,3,25,5,1,5,4,2,5,3,34,4,3
12 ұпай үшін:6,5,1,6,4,2,6,3,3,5,5,2,(4,4,4 )
Де Меренің қатесін француз математигі Блез Паскаль (1623-1662) көрсетті. Де Мере көрсетілген комбинацияларды өзара тең мүмкіндікті оқиғалар емес. Мысалы, (6,4,1) комбинайиясын 6 түрлі тәсілмен алуға болады: 6,4,1,6,1,4,4,1,6,4,6,1,1,6,4 (4,4,4)
Комбинациясының тек бір ғана мүмкіндігі бар.
ХVII ғасырдың екінші жартысында Паскаль мен Ферма арасындағы хат алмасу кезінде ғалымдар құмар ойындарда кездесетін заңдылықтарды ғылыми тұғыдан негіздеп бақты. Тарихшы ғалымдар ықтималдық теориясының пайда болуын осы хат алысулардан бастау алады деп бағалайды. Бұл теорияның дамуына нидерланд математигі Х.Гюйгенс (1629-1695), неміс ғалымы Г.В. Лейбниц (1646-1716), швейцар математигі Я.Бернулли (1654-1705) және өзгелер қомақты үлес қосты. XVIII ғасырда жаратылыстану және тұрмыс-тіршілік мұқтаждадықтары (бақылау қателіктері теориясы, оқ ату теориясы есептері, статистика мәселелері және т.с.с ) ықтималдықтар теориясының дамуын жаңа сатыға көтерді.
Ықтималдықтар теориясында аналитикалық тәсілдерді қолдануда үлкен үлес қосқандар қатарында А.Муавр (1667-1754), П.С. Лаплас(1749-1827), К.Гаусс (1777-1855), С. Пуассон (1781-1840) сынды ғұлама математиктер болды.
Ал, XIX-XX ғасырларда ықтималдықтар теорисы мен математикалық статистиканың дамуына орыс математикьтерінің қосқан үлесі зор. Олардың қатарына П.Л. Чебышев(1821-1894), А.А. Марков (1856-1922), А.М. Ляпунов (1857-1918), С.Н. Бернштейн (1880-1968), А.Я. Хинчин (1894-1959), А.Н. Колмогоров (1903-1987) және өзгелерді қосуға болады. Мәселен, А.Н. Колмогоров ықтималдықтар теориясын аксиоматикалық жолмен тұрғызды.

1.2 Комбинаториканың негізгі элементтері.
Комбинаторика ақырлы жиындардың құрастыру әдістерін зерттейді.
Комбинаторика екі түрлі есептерді зерттейді: таңдау есептерін және орналастыру есептерін.
Таңдау есептерінде берілген жиыннан элементтерді таңдап алудың ережелері анықталады.
Орналастыру есептерінде берілген элементтерден жаңа жиындар құралады.
Кез келген жағдайда комбинаторикалық конфигурациялардың құрастырылуымен байланысты болады, сондықтан комбинаторикалық конфигурациялардың бар болуы, конфигурация санын зерттеу, құрастыру алгоритмі сияқты мәселелерді шешуге тура келеді.
Комбинаторикалық конфигурациялардың негізгі түрлеріне мыналар жатады: біріктіру, алмастырулар, терулер, орналастырулар, композициялар, бөліктеулер.
Мысал келтірсек. Айталық, a,b,cжәне d элементтері берілсін.Осы элементтерден 2 элемент алып, бір бірінен айырмашылығы ең болмағанда бір элементте болатын қосылыстар жасалық: ab,ac,ad,bc,cd. Міне берілген 4 элементтен 2-ден жасалған және айырмашылықтары элементтерде болатын қосылыстар осылар. Осындай қосылыстар терулер деп аталады.Берілген n элементтен k-дан жасалған терулер дегеніміз - бір-бірінен айырмашылықтары ең болмағанда бір элементінде болатын қосылыстар.
n элементтен k-дан жасалған терулер санын Cnk деп белгілейміз. Мысалы, жоғарыдағы терулер саны C42=6
Теорема. Мына формула орынды

Cnk=nn-1n-2...(n-k+1)1∙2∙3∙k (1)

формула сырт пішініне қарағанда күрделі көрінгенмен оны есептеген кезде өте оңай жүргізіледі: бөлшектің алымына төменгі индекстен басталған және бірінен кейін бірі 1-ге кеміп отырған натурал сандардың көбейтіндісі және де көбейткіштерінің саны жоғарғы индекске тең, ал бөлшектің бөлімінде 1-ден бастап жоғарғы индекске дейінгі натурал сандардың көбейтіндісі тұр. Мәселен,
C103=10∙9∙81∙2∙3=10∙3∙4=120

Демек, 10 элементтен 3-тен 120 әр түрлі терулер жасауға болады.Тәжірибелік есептерде теру қосылысы n элементтен k элементін алу жағдайында пайда болады. Мәселен, қалың жұртшылыққа кең тараған 36-дан 5 спортлото ойынындағы әр билетті толтыру - 36-дан 5-тен жасалған теру. Демек, барлық мұндай терулер саны
C365=36∙35∙34∙33∙321∙2∙3∙4∙5=6∙7∙34 ∙33∙8=376992

Мұны 36-дан 5 спортлото билеттерін әр түрлі толтырулардың барлық жағдайлары деп те түсіну керек.

Мысал: 10 сауын сиырын олардың сүттілігіне не басқа да өзгешеліктеріне қарамай екі сауыншыға тең етіп қанша әдіспен бөліп беруге болады?
Шешуі: Мұнда 10-нан 5 элементті алу екендігін түсіну қиын емес. Сонда сұрап отырған әдістер саны - C105
(1) формула бойынша есептесек C105=504
Теру сандарының мынадай қасиеттері бар.
1. Теру саны үшін факториал таңбасын пайдаланып,
Cnk=n!k!(n-k)! (2)
2.
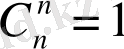
3.
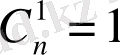
4.
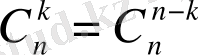
Бұл теңдіктердің орынды болатындығы (2) теңдіктен көрініп тұр. Теру саны арқылы Ньютон биномы деп аталатын жіктеуді келісті түрде жазуға болады:

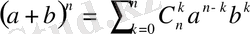
Сөйтіп, биномдық жіктеудегі коэффициенттер - теру сандары. Ескерте кетелік, келісім бойынша

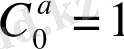
теңдігін анықтама есебінде қабылдайды.
Орналастырулар. Бұл қосылыстың анықтамасын беруден басталық.
Анықтама. n элементтен k-дан алынған орналастырулар дегеніміз бір-бірінен өзгешеліктері әрі элементтерінде, әрі элементтердің реттерінде болатын қосылыстар.Мәселен, a,b,c,d төрт элементтерінен екіденжасалған орналатырулар мыналар:

аb, ac, ad, bc, cd, bd,
ba, ca, da, cb, db, dc.

барлығы - 12. сөйтіп, орналастырулар әрі теру болады. Практикалық есептерде орналастырулар n элементтерден k элементті бірдіндеп алғаннан келіп шығады.
n элеметтен k-дан жасалған орналастырулар санын әдетте деп белгілейді.
Теорема. Орналастырулар саны үшін

Ank=nn-1n-2...(n-k+1) (3)

формуласы орынды.
Теру санының формуласын қолдануда оңай: төменгі индекстен бастап көбейткіштер құру керек; келесі көбейткіш ілгеріден бірді алып тастағаннан шығады; көбейткіштердің саны жоғарғы индекске тең. Mәселен, бұл санды 10 қозыны 3 көгендедің барлық мүмкін болатын жағдайлары деп те түсінуге болады, өйткені қозыларды көгенге біртіндеп көгендейді.
Алмастырулар. Анықтама:n элементтен n-нен жасалған орналастыруларды n элементтен жасалған алмастырулар дейді.Алмастырулар P саны үшін таңбалауы қолданылады.
Теорема. Алмастырулар саны үшін мына формула:
Pn=n!=nn-1n-2...1 (4)
орынды.
Сонымен, n элементтен жасалған алмастырулар дегеніміз, бір-бірінен өзгешеліктері элементтердің реттеріндеғана болатын қосылыстар.Ескерте кетелік, теру,орналастыру және алмастыру сандарының арасында мынадай байланыс бар.
Cnk=AnkPk

Бір-бірлеп алынған комбинация. Бұл қосылыс жайында оқулықтарда аз айтылады, ал оның қолданылуы бірінші сыныптың бағдарламасынан бастап кездеседі деп айтсақ, жаңылыспаған болар едік. Айталық, k элементтер тобы берілсін: бірінші топта n1 элемент, екінші топта n2 элемент және т.б. , k -ші топта nk элемент болсын делік:

Бірінші топ элементтері: a1,a2,...an
Екінші топ элементтері: b1,b2,...bn.
k-ші топ элементтері: c1,c2,...cn.

Бірінші топтан бір элемент - аі1, екінші топтан бір элемент - bі2 т.т.,k-ші топтан бір элемент - сіk алып, соларды алынған реттеріне қарай бір-бірлеп жазып, мынадай қосылыс жасалық:
ai1,bi2,...,cik

Міне осындай қосылысты бір-бірлеп алынған комбинация деп аталады.
Теорема. Жоғарыдағы элементтердің топтарынан жасалған бір-бірлеп алынған комбинациялар саны n1·n2·n3·nk көбейтіндісіне тең.Бұл теореманы комбинаториканың негізгі теоремасы деп те атайды.
Бұлай деп аталатын себебі, бұл теоременың идеясы қандай да болмасын комбинаторика санын есептеуге қатысады. Мысал: Төрт ойын сүйегі лақтырылған. Сүйектердегі ұпайлардың бірдей болу ықтималдығы қандай? Шешуі: Төрт ойын сүйегін лақтырғанда пайда болатын жағдайды (I,j,k,l) деп қарастыруға болады. Әр сүйекте 6 ұпай бар. Демек, негізгі теорема бойынша барлық жағдайлар саны n=64. А - барлық сүйектердегі ұпайлар бірдей. Сонда A-ға қолайлы жағдайлар алтау: (1, 1, 1), (2, 2, 2),...,(6, 6, 6).
Демек,
PA=664=1216

Мысал: Урнада 3 қара және 2 ақ шар бар. Жәшіктен қандай да бір 2 шар алынған. Сол алынған шарлардың түстері әр түрлі болу ықтималдығы қандай?
Шешуі: Тәжірибе 5 шардан 2 шар алу. Демек, барлық жағдайлар саны - C52=5∙2=10 .
А - алынған екі шардың түстері әр түрлі. Сонда, А-ға қолайлы жағдайда 1 ақ және 1 қара шар болуы керек. Негізгі теорема бойынша қолайлы жағдайлар саны - C31C21=3∙2=6 ,

PA=610=0.6
Мысал: Трамвай аялдамасында 8 жолаушы тұрған. Бұлар маршрут бойынша келген трамвайдың екі вагонына қалай болса солай отырған. Әр вагонға жолауларшың төрт-төрттен отыру ықтималдығы қандай?
Шешуі: Сегіз адамның әрқайсысы екі вагонның біреуіне отыра алады. Сонда, барлық жағдайлар саны, комбинаториканың негізгі теоремесы бойынша, 28 дәрежесіне тең. Ал, қолайлы жағдайлардың санын есептеу үшін 8-ден 4 принципін қолдануға болады- C=70. Демек ізделінде ықтималдық P=7028≈0.2734

2. Комбинаторика элементтерін пайдаланып есептер шығару
2.1 Комбинаторикалық есептерді шешудің негізгі тәсілдері

Іс жүзінде адамға заттардың өзара орналасуының барлық мүмкін жағдайларын есептеуге немесе қандай да бір іс-әрекеттің барлық мүмкін нәтижелерін және оны орындауға қажетті барлық мүмкін тәсілдер санын есептеуге тура келеді. Мысалы: әр түрлі 5 кітапты екі оқушыға неше түрлі тәсілмен үлестіріп беруге болады? Футболдан әлем біріншілігінде жартылай финалға шыққан 4 команда арасында алтын, күміс, қола медальдары неше түрлі тәсілмен иемделінеді және т.с.с.
Бұл есептерде заттардың өзара орналасуының немесе іс-әрекеттің барлық мүмкін комбинациялары қарастырылады. Сондықтан, мұндай есептерді комбинаторикалық есептер деп атайды.
Комбинаторлық әдістер физика, химия, биология, экономика, тағы басқа ғылымда қолдануға болады. Ал комбинаторикалық есептерді шешуде үйретуде математика саласын комбинаторика деп атайды.
Комбинаторика есептерін шешуде қолданатын өзіндік заңдылықтар мен формулалар бар.
A жиынының элементтері санын n(A)арқылы белгілейді. Мынадай заңдылық орындалады:
Қосу ережесі.
Кез келген санаулы элементтері бар А және В жиындары үшін
nA∪B=nA+nB-n(A∩B) (1)
теңдігі орындалады.
Ал бұдан
nA+nB=nA∪B+n(A∩B) (2)

математикалық индукция принципі бойынша бірнеше қосылғыштарға жазып шығуға болады.

(3)

Есеп.Сыныптағы 32 оқушының 14-і мектепте өткен футбол турниріне, 10-ы баскетбол турниріне және 8-і волейбол ойынынан жарысқа қатысқан. Мұнда 6 оқушы әрі футбол, әрі баскетбол жарысына, 5 оқушы әрі футбол, әрі волейбол жарысына, 4 оқушы әрі баскетбол, әрі волейбол турниріне, ал 3 оқушы барлық үш ойыннан жарысқа қатысқан.
Сынып оқушыларының нешеуі осы турнирлердің бірде-біреуіне қатыспаған?
Талдау:
Эйлер - Венн диаграммасын қолданайық.
А - футболға қатысқан оқушылар жиыны,
В - баскетбол,
С - волейбол,
U - сыныптағы барлық оқушылар жиыны болсын. Есеп шарты бойынша:

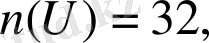
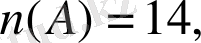
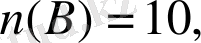
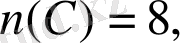
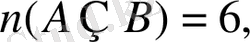
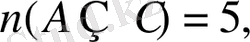
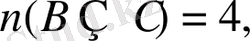
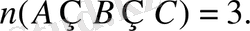
(3) формула бойынша

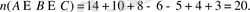
Сыныптағы оқушылардың жарыстың қандай да бір түріне қатысқандарын біліп алдық. Онда сыныпта 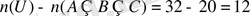оқушы жарыстың бірде-бір түріне қатыспаған.Өмірдегі сан мыңдаған оқиғаларға математикалық тұрғыда қортынды жасауға арналған негізгі тәсілдердің біреуі мүмкіндіктерді санау немесе комбинаторика болып табылады. Жиынның элементтерінің санын, оларды реттеу санын табу, барлық мүмкін болмыстардың санын табу қажеттігі өмірде көптеп кездеседі. Осы мәселені оңтайлы шешуге бізге мүмкіндік санау тәсілдері немесе комбинаторика көмектеседі.Математикалық оқиғаларды көбінесе жиындармен жиындарға қолданылатын амалдар арқылы белгілеп, мүмкіндіктер санын қосу және көбейту ережесін қолданып есептеу комбинаториканың негізі болады да комбинаторикалық мазмұнды есептерді шешу ісі көбінесе оны қандай бір жиынның элементтерінің санын, бұл элементтерді белгілі ретпен орналастыру мүмкіндігін немесе оның ішкі жиындарын санау арқылы шығарылатын болады.Енді комбинаторикалық есептерді шешудің негізгі тәсілдеріне тоқталсақ:
1. Қосу ережесі. Дербес жағдайдағы мүмкіндіктер санын есептеп, немесе ішкі жиынның элементтері мен оларды орналастыру сандарын есептеп өзара қосу және тізбе түрінде жазып өсу заңдылығын табу тәсілдері қолданылады. Бұл тәсілге жиындарға қолданылатын амалды пайдалансақ жиындардың бірігуінің элементерінің санын табуға арналған формуласын пайдаланамыз. Ал тізбекті пайдалансақ өзгеру заңдылығын, рекуренттік қатынасты байқау деген сияқты тәсілдер таңдауға тура келеді.
Мысал1: 10 тор көзді жолақтың сол жақ шеткі көзіндегі тас оңға қарай 1 не 2 аттап көшу арқылы оң жақ шеткі көзге неше әр түрлі маршрутпен жетуге болады?
Шешуі: 2-ші көзге 1, 3-ші көзге 2 тәсілмен келе алады да 3- көзден бастап әр көзге оның алдындағы 2 көзден 1 не 2 аттап түсе алады. k-інші көзге келетін маршрут саны , рекурент формуласы бойынша есептеледі. Олай болса: Жауабы: 89-әр түрлі маршрут
Мысал2: Сыныптағы 25 оқушының 15-і математика 9-ы физика пәнінен факультетив сабаққа қатысады да 6-ы бұл екеуінің қай-қайсысына қатыспайды. Екі факультетивке қатар қатысатын және тек математикаға қатысатын оқушылар қанша?
Шешуі: А- математикаға, В- физикаға қатысатын оқушылар жиыны болса 25-6=19 болғандықтан екі фалультетивке қатар қатысатындар саны 15+9-19=5 болады да тек математикаға ғана қатысатындар 15-5=10 оқушы.
Мысал3: Алдындағы келтірілген 1 б) мысалдағы үшбұрыштар санын табайық.
Шешуі: Үшбұрыштың табанының сол жақ төбесі астыңғы табан бойындағы түйін нүктелерінде болатын үшбұрыштар санын оң жағынан бастап санап қоссақ, сәйкес 1,2,3,4,5,6 болады да қосындысы 21-ді 2 еселеп алсақ суреттегі барлық үшбұрыштардың санын береді.Жауабы: 42 үшбұрыш.
Мысал4: нүктелер тізбегінің санын квадрат сандар, ал төменгітізбектерді сәйкесінше үшбұрыш сандар және бестік сандар деп алайық.
а) 7- ші квадрат, үшбұрыш, бестік сандарды тап.
б) Квадрат, үшбұрыш, бестік сандарының заңдылығын тауып әр қайсысының 10- шы, 50- ші сандарын тап.
Шешуі:Квадрат сандардың заңдылығы айқын. Үштік сандар 2-сінен бастап алдыңғысына сәйкес 2,3,4 деген сияқты тізбектелген бүтін сандармен қосылып отыратындықтан 7-шісі 1+2+3+4+5+6+7=28 n-інші сан 1+2+3+...+n болады. Бестік сандар саны: 1+(1+3) = 2 + 3∙1, 5+(1+3+3) = 3+ (1+2)∙3 .
2. Көбейту ережесі
Оқиға немесе жиынның әр элементінің мүмкігдігін есептеп барлық мүмкіндікті табу тәсілі көбейту ережесі арқылы жүзеге асырылады. Көбейту ережесін жиын арқылы анықтасақ n- элементтен тұратын А, m элементтен тұратын В жиындарының әр қайсысынан бір бір элемент алып құрастыруға болатын a,bпарлар саны 1-ге тең. Осындай барлық мүмкін парлар жиынын А, В жиындарының Декараттық көбейтіндісі деп атап деп белгілейді.
Есеп.
Асханада І-ші тамақтың екі түрін , ІІ тамақтың үш түрін және екі түрлі десерт ұсынады. Асхана қанша түрлі түскі тамақ ұсынуға болады?

Бұл тәсіл графиктік жолмен кескінделген. Бұл схеманыталдау ағашы деп атайды.. . .
.
Сонымен, асханашы 12 түрлі түскі тамақ ұсынады.
Мысал1: 21 оқушысы бар сыныптың оқушыларын неше әр түрлі тәсілмен сапқа тұрғызуға болады?
Шешуі:1- ші орынға 21- оқушының кез келгенін , 2- ші орынға 1- ші орынға тұрған оқушыдан басқа 20 оқушының кез келгенін, деген сияқты 21-інші орынға қалған 1 оқушыны таңдау арқылы 21- элементтен тұратын парлар таңдау керек болатындықтан сапқа тұрудың барлық мүмкіндігіболады.
Мысал-2: жиынтығынан солдан оңға қарай бағытпен АСТАНА сөзін әр түрлі неше тәсілмен оқуға болады?
Шешуі: С- әріптерінің қтан әр қайсысына 1, Т әрпінің әр қайсысына екі С- ның қайсысынан да баруға болатындықтан әр қайсысына 2 деген сияқты келуге болатын мүмкіндіктер бар болғандықтан барлық мүмкіндіктер саны Жауабы: Әртүрлі 36 тәсілмен оқылады.
Мысал-3: 6 лампа арқылы бөлмеге неше тәсілмен жарық беруге болады? (әр лампада жеке ажыратқыш бар)
Шешуі: 6 лапаның әр қайсысында бөлмеге жарық беруге қатысудың жану, сөну деген 2 мүмкіндігі болатындықтан есептің жауабы .
Мысал-4: 0,1,2,3 цифрларын пайдаланып неше 5 таңбалы сан жазуға болады?
Шешуі: 5 таңбалы санның алдыңғы цифры 0-ден басқа 3 мән, басқа разриядтағы цифрлар берілген 4 цифрдың төртеуін де қабылдай алатындықтан бес таңбалы сан .
Мысал-5: Барлық үш таңбалы жұп сан нешеу?
Шешуі :Бұл есептегі оқиға үщ таңбалы жұп сан жазу, оқиға элементтері -үш таңбалы санның цифрлары, жүздік орындағы цифрдың мүмкін мәндері 0-ден басқа 9 цифр, 10-дық орындыкі барлық 10 цифр, ал бірлік орындағы цифр жұп болатындықтан оның мүмкін мәндерінің саны 5 болатыны түсінікті. Сондықтан есептің жауабы .
Мысал-6: 10 оқушыдан 3 оқушыдан тұратын кезекшілер тобын неше әр түрлі тәсілмен таңдап алуға болады.
Шешуі:Оқиға үш элементі жиын таңдау. Бірінші кезекшіні 10, екіншісін 9 оқушыдан, үшіншіні 8 оқушыдан таңдаймыз. Көбейту ережесі бойынша барлық мүмкіндік саны . Бірақ бұл санға А, В, С үш оқушыдан тұратын кезекшілер тобы, таңдалу ретіне байланысты рет есептеліп тұрғанын ескерсек есептің жауабы 720:6 = 120.
Мысал-7: 8х8 шахмат тақтасында бір ақ, бір қара көзден тұратын пар көзді:
а) неше әр түрлі тәсілмен белгілеуге болады?
б) Бұл екі көз бір баған немесе жол бойында болатын мүмкіндіктер?
в) Бір баған немесе жол бойында болмайтын мүмкіндіктер саны қанша?
Жауабы: Ақ көзді таңдау мүмкіндігі 32. Таңдаған ақ көзбен бір баған немесе бір жол бойында болатын қара көз 4+4=8 . Барлық мүмкіндік саны 32∙8=256
Мысал-8: 5 әр түрлі реңді ленталардан 3 көлденең жолақтан құралған жалауды неше әр түрлі тәсілмен жасауға болады?
Жауабы: Әр түрлі үш реңнен жасалатын, және шеткі екеуі бірдей , ортаңғысы өзгеше болатын екі жағдайды қарастыр.
2.2 Қайталамалы таңдамалар үшін қолданылатын комбинаторика формумалары

Қайталамалы орналастырулар.
Осы уақытқа дейін элементар жиыннан орналастырулар жасағанда одан алынған элемент жиынға қайыра енбейтін еді, ондай орналастырулар қайталанбайтын орналастырулар болады. Біз енді қайталамалы орналастыруларды, яғни жиыннан алынған элемент сол жиынға қайыра енетінін қарастырамыз, мысалдар келтірейік.
1-мысал:1,2,3 цифрларынан екі таңбалы неше сан жазуға болады?
Шешуі. Бұл есепті екі тәсілмен шешуге болады.
Бірінші тәсіл: цифрлары қайталанбайтын әр түрлі екі таңбалы сандарды
A32=3∙2=6 тәсілмен жасаймыз, олар:
12,21,31,13,23,32
Екінші тәсіл: цифрлары қайталанып отырған әр түрлі екі таңбалы сандарды біртіндеп жазсақ, мыналар шығады:
11;21;31
12;22;32
13;23;33
Яғни олардың барлық саны 3∙3=9 болады. Басқаша айтқанда цифрдың әрқайсысы да 3 тәсілмен алынады, сонда бірінші алынған цифр әр жолы екінші цифрмен комбинацияланады, сөйтіп, екі цифр комбинациясын
3∙3=32=9
Тәсілмен аламыз. Бұл мысалды әрі қарай да кеңейте беруге болады.
2-мысал. Осы 1,2,3 цифрларынан қайталамалы орналастырулар тәсілімен үш таңбалы, K таңбалы неше сан құруға болады?
Шешуі. Үш таңбалы санның бірінші цифрын 3 тәсілмен, екіншісін де 3 тәсілмен алуға болады.
Сонда, алдыңғы екі цифрлы санды 3∙3=32 тәсілмен аламыз. Бұлардың әрқайсысы үшінші цифрмен комбинацияланады. Сонда үш цифрлы санды 32∙3=33=27 тәсілмен құруға болады. Осылайша талқыласақ, осы үш цифрдан 4 цифрлы сандарды 34=81 тәсілмен, ал K цифрлы сандарды 3K тәсілмен құруға болатынын байқау қиын емес.
Енді есептің шартын өзгертіп, яғни берілген 1,2,3 цифр орнына 1,2,3,...,N цифрды алайық.
Сонда N цифрдан әр түрлі екі цифрлы сандарды N∙N=N2 тәсілмен, әр түрлі үш цифрлы сандарды N2∙N=N3 тәсілмен, ал K цифрлы әр түлі сандарды NK тәсілмен құруға болады. Сонымен, мынадай қорытындыға келеміз:
Элементтері қайталанып келетін N элементтен K-дан алынған орналастырулар
PNK=PK

формуласымен өрнектеледі.
Мұны қайталамалы орналастырулар немесе қайталамалы іріктеме формуласы деп аталады. Қайталанбайтын орналастырулар мен салыстыруларды айтқанда іріктеме көлемі K=Nболатын.
Ал, элементтері қайталанатын орналастырулар мен алмастырулар үшін KN, K=Nжәне KN болуы мүмкін. Бұл факт жоғарыда келтірілген мысалдан айқын көрініп тұр.
3-мысал. Соғылатын телефонның номері 4 цифрдан құралған. Ол номердің:
а. Барлық цифрлары әр түрлі болып келу ықтималдығын.
ә. Барлық цифрларының жұп болып келу ықтималдығын анықтау керек.
Шешуі: а. 4 таңбалы нөмердің әр цифры 0,1,2,3,4,5,6,7,8,9 цифрларының кез келгені болуы мүмкін. Олай болса, әр түрлі төрт таңбалы нөмрлердің барлық саны 104 болады. Олар 0000-ден 9999-ға дейінгі нөмірлер саны. Бұлардың ішінде бізге қажеттісі - цифрлары әр түрлі төрт таңбалы сандар, олар 10 цифрдан 4тен алынған орналастырудың санына тең, яғни

А104=10∙9∙8∙7

бұл- оқиғаның пайда болуына қолайлы жағдайлар саны. Оқиғалардың барлық тең мүмкіндікті, ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.