ГАУСС ФОРМУЛАСЫ

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 17 бет
Таңдаулыға:

МАЗМҰНЫ
КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. 3
1.ГАУСС ФОРМУЛАСЫ
1.1. Гаусс тарихына шолу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 5
1.2.Гаусс формуласын дәлелдеу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... . 6
1.3.САТЖ Гаусс әдісімен шешу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 7
2. ВАЛЛИС ФОРМУЛАСЫ
2.1.Валлис формуласының шығуы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .11
2.2.Эйлердің синустар шексіз көбейтіндісі негізінде дәлелдеу ... ... ... ... ... ... 12
3. САННЫҢ ТРАНСЦЕНДЕНТТІГІ
3.1.Тарихы мен қасиеттері ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...14
3.2.Трансценденттік сандар ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... ... . 16
ҚОРЫТЫНДЫ ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 18
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ ... ... ... ... ... ... ... . ... ... ... ... ... ... ... .. 19

КІРІСПЕ

Курстық жұмыстың өзектілігі:

XVIII ғасырдың соңында Германиада бір сабақта мұғалім оқушыларына "1 - ден 100 ге дейінгі натурал сандардың қосындысын табуды" тапсырыпты. Оқушылардың біреуі ізделген қосынды 5050-ге тең деп жауап беріпті. Бұл оқушы кейіннен аты әлемге әйгілі болған математиктер королі Карл Фридрих Гаусс екен. Салу есептері ежелгі математиктердің еңбектері арасынан елеулі орын алған. Өйткені, бұл кезеңде барлық математикалық деректер сызба көмегімен геометриялық тілде негізделген. Сызғыш пен циркульді пайдаланып көпбұрыштарды, оның ішінде дұрыс көпбұрыштарды салу мәселесі немістің ұлы математигі Карл Гауссқа дейін өз шешімін таппай келді. Бұл мәселені тек 1801 жылы ғана К. Гаусс алгебралық жолмен толық шешті. Оның дәлелдемесі бойынша дұрыс n-бұрышты циркульді және сызғышты пайдаланып салу үшін n=2m , P1∙P2 ... ... .∙Pk, mEuroZ, m=0,
P1,P2, ... ... .∙Pk22+1, ал 7 мұндай түрде жазылмайды, яғни жетібұрышты циркулді және сызғышты пайдаланып салуға болмайды.
Валлис формуласы-бірінші формулалардың бірі, онда сан рационалды сандардың кезектілігі түрінде көрсетілген.
Дегенмен , ол өте қолданылмайды , өйткені, іс жүзінде оны пайдалану мағынасыз.
1655 жылы Джон Валлис PI санын анықтау үшін формуланы ұсынды.
Дж. Валлис шеңбер ауданын есептеуді қарастырды . Бұл жұмыс өте баяу жүреді, сондықтан PI санын практикалық есептеу үшін Валлис формуласы аз жарамды. Алайда, ол түрлі теориялық зерттеулерде пайдалы, мысалы, Стирлинг формуласын шығару кезінде. Валлис тарихи формуласы шексіз шығармалардың алғашқы мысалдарының бірі ретінде маңызды болды.
Трансценденттік сан (лат. transcendere-ауысу, асып кету) -- бұл нақты немесе кешенді сан, ол алгебралық емес-басқа сөзбен айтқанда, ол рационалды коэффициенттермен (нөлге тең емес) көп мағыналы емес сан.
Трансценденттік сан, бүтін коэффициенттермен көп мағыналы түбірі болып табылмайтын сан. Ол тек қана шындықты ғана қарастырады, сонымен қатар, олардың бар-жоғын, оның ішінде Ж. Лиувилль (1844) өзі байқаған факт негізінде негіздеген: иррационалдық алгебралық сандар иррационалдық сандармен "өте күшті" жақындауға жол бермейді;
С. I. Кантор (1883) : ол кейбір барлық алгебралық жиындардың санақсыздығын анықтайды, бұл шын мәнінде континуумның көптеген қуатын құрайтынын дәлелдеді.
Э. Борель (1898): шара теориясының алғашқы ұғымдарын енгізе отырып, трансценденттің "барлығы дерлік" нақты сандары, алайда бұл сан трансцендентті болып табылатындығының дәлелі өте қиын міндетті құрайды. е санының трансценденттілігін Ш. Эрмит дәлелдеді (1873). Алгебралық және логарифмдердің трансценденттілік сандарды дәлелдеген математик Ф. Линдеман (1882). Трансцендентті санының дәлелдеді А. О. Гельфонд (1929). Ол. математик Т. Шнайдер бір мезгілде 1934 жылы 0 және 1-ден ерекшеленетін алгебралық αβ, α-трансцендентті және алгебралық иррационалдық β (осылайша Гильберттің жетінші мәселесін шеше отырып) екенін дәлелдеді.
Ғылыми жұмыстарымның нәтижесінде қазіргі математиканың негізгі әдістерінің бірі болып табылатын, техника ғылымдарында қуатты құрал болып табылатын векторлық әдісті меңгереміз.
Курстық жұмыс мақсаты:
Гаусс Әдісі болып табылаты классикалық әдісімен шешу сызықтық алгебралық теңдеулер жүйелерін (СТЖ). Ол үшін ыңғайлы, жылдам шешім шектелген мөлшері бойынша матрицалау.Гаусс әдісі екі жолмен шешіледі: тікелей және кері. Тікелей барысын деп аталады дәйекті келтіруге СТЖ - үшбұрышт түрі, яғни нөлдеу мәндерін тұрған, басты диагональ. Кері жүріс білдіреді дәйекті болуы айнымалылардың мәндерін білдіре отырып, әрбір айнымалы арқылы өтетінін.
Үйрену тәжірибеде қолдану Гаусс әдісі қарапайым болып келеді ьо, жеткілікті қарапайым ережелерін көбейту, қосу және азайту амалдарын қолдану.
Сол баяғыда PI - қатынас саны енгізілді шеңбер ұзындығы оның диаметріне және циркуль және сызғыш салу мүмкіндіктері берілген алаңы бар шаршы шеңбер. Бұл шеңбер квадраты туралы міндет. Помо кезінде құрылысты мұқият талдау- циркуль щи және сызғыштар көз жеткізуге болады, егер ол мүмкін болса, саны PI алгебралық болып табылады. Сондықтан, әрине, пайда болды-кает саны осындай болып табылады ма деген сұрақ. Жауабы бар ежелгі дәуірде берілген бұл сұраққа,тек өткен ғасырдың соңында Ф. Линде 1882 жылы берді-ман. Ол PI алгебралық емес екенін дәлелдеді, яғни трансцендентті және, іздер-шеңбердің квадраты туралы есеп дұрыс емес.

Міндеттері:
Гаусс әдісі туралы мәлімет жинау.
Гаусс формуласының қолданылуы, дәлелденуі.
Валлис формуласын қорыту.
Эйлердің синустар шексіз көбейтіндісі негізінде дәлелдеуі.
Трансценденттік сандарды қарастыру.

Курстық жұмыстың құрылымы: Курстық жұмыс кіріспеден, үш бөлімнен тұрады. Кіріспеде курстық жұмыстың өзектілігі мен мақсаты көрсетілген. Бірінші бөлімде гаусс әдісінің тарихы мен дәлелденуі қарастырылған,тақырып бойынша есеп қарастырылған. Екінші бөлімде валлис формуласы қорытылған, Эйлердің синустар шексіз көбейтіндісі негізінде,интегралдауда дәлелденген, үшінші бөлімде санның трансценттілігінің құрылымы қарастырылған.Қорытынды жасалынды.

ГАУСС ФОРМУЛАСЫ

Гаусс тарихына шолу
Компекс сандарды математикаға енгізудің бірінші қадамдарын XVI ғасырда үшінші және төртінші дәрежелі теңдеулерді шешуге байланысты италия математиктері Кардано және Бомбелли жасады. Бірақ, тек XIX ғасырда ғана Гаусс комплекс санның нақты түсінігін бере алды. XIX ғасырда комплекс сандардың негізінде құрастырылған комплекс айнымалылы функциялардың теориясы математикалық талдауды жаңа нәтижелермен байытты, және келешекте механика және физиканың маңызды бөлімдерін зерттеуде күшті құрал болып табылды.
Жаңа сандық жүйені құрастыру үшін геометриялық тұрғыларды пайдаланған ыңғайлы. Нақты сандар түзудегі нүктелермен бейнеленеді, бұл бейнелеу түзудің барлық нүктелер жиыны мен нақты сандар жиыны арасындағы бірмәнді сәйкестікке негізделеді. Жаңа сандарды нақты сандар жұптарының көмегімен құрастыру керек, және жаңа сандық жүйе нақты сандар жүйесінің кеңейтілуі болып табылады.
Сандық әдістер есепті шешудің қуатты математикалық құралдарының бірі болып табылады. Қарапайым сандық әдістерді біз барлық жерде қолданамыз, мысалы, қағаз парағындағы квадрат түбірін аламыз. Күрделі сандық әдістерсіз жауап ала алмайтын міндеттер бар; классикалық мысал - Нептунның уранның қозғалыс ауытқулары бойынша ашылуы.
Сызықты алгебралық теңдеулер жүйесі дифференциалдық, интегралдық немесе сызықты емес (трансценденттік) теңдеулер жүйелерімен сипатталатын бірқатар қолданбалы есептерді шешу кезінде аралық немесе түпкілікті кезең ретінде туындайды. Олар математикалық бағдарламалау, мәліметтерді статистикалық өңдеу, функциялардың аппроксимациясы есептерінде, шеткі дифференциалдық есептерді соңғы айырмалықтар әдісімен дискреттеу кезінде, соңғы элементтер әдісімен, проекциялық әдістермен, шекаралық элементтер әдістерінде, Дискреттік ерекшеліктерде, ұшу аппаратының аэродинамикалық компоновкасының панельді әдісінде және т. б. пайда болуы мүмкін.
Пайда болатын жүйелердің матрицалары әртүрлі құрылымдар мен қасиеттерге ие болуы мүмкін. Қазір бірнеше мыңға жуық толық толтыру матрицалары бар сызықты алгебралық теңдеулер жүйесін шешу қажеттілігі бар. Соңғы элементтер әдісімен бірқатар қолданбалы есептерді шешу кезінде бірқатар жағдайларда лентаның бірнеше ондаған мың жарым ені мыңға дейін оң анықталған ленталық матрицаларына ие жүйелер пайда болады. Және, ақырында, бірқатар есептерде соңғы айырмалар әдісін қолданған кезде миллионның сиретілген матрицалары бар айырымдық теңдеулер жүйесін шешу қажет.
Сызықтық теңдеулер жүйесін шешудің ең көп таралған әдістерінің бірі Гаусс-Зейдель әдісі болып табылады.

1.2. Гаусс формуласының дәлелдеу
Бізде n сызықтық теңдеулер жүйесі бар болсын:

a11x1 + a12x2 + a13x3 + ... a1nxn = b1
a21x1 + a22x2 + a23x3 + ... a2nxn = b2
a31x1 + a32x2 + a33x3 + ... a3nxn = b3
... ... ... ... ...
am1x1 + am2x2 + am3x3 + ... amnxn = bn ... ... ... ... ...

мұнда xi-белгісіз, aij - белгісіз коэффициенттер, bi-теңдеулердегі бос мүшелер, I, j 1-ден n-ге дейінгі мәндер жүгіреді.
Тапсырманың мақсаты-aij және Bi xi табу.
Гаусс әдісінің мәні кейбір операциялардың көмегімен теңдеулердің бастапқы жүйесін қарапайым жүйеге келтіруге болады. Бұл қарапайым жүйе үшбұрышты көрініс табады:
a11x1 +
a12x2 +
a13x3 +
...
a1nxn = b1

a22x2 +
a23x3 +
...
a2nxn = b2

a33x3 +
...
a3nxn = b3
...

...
amnxn = bn
Бұл жүйенің ерекшелігі-I нөмірлі жолдарда ji кезіндегі барлық aij коэффициенттері нөлге тең.
Егер біз теңдеулердің жүйесін осындай үшбұрыш түріне келтіре алатын болсақ, онда теңдеулерді шешу оңай. Соңғы теңдеуден xn= Bn ann табамыз. Содан кейін оны алдыңғы теңдеуге қойып, xN-1 табамыз. Табылған екі шешімді келесі теңдеуді қойып, xn-2 табамыз. Және X1 таппайынша, шешім неден аяқталады. Мұндай рәсім кері айдау деп аталады.
Енді жүйенің үшбұрышты болуына қалай қол жеткізу керек деген сұраққа көшеміз.
Сызықтық алгебрадан, егер теңдеулер жүйесінің кейбір жолына осы жүйенің кез келген басқа жолдарының кез келген сызықтық комбинациясын қосса, онда жүйенің шешімі өзгермейді. Жолдардың сызықтық комбинациясы деп әрқайсысы кейбір санға көбейтілетін жолдар сомасы түсініледі (негізінде кез келген).
Екінші жолда X1 мүшесі жоқ теңдеуді алу керек. Осы жолға m санына көбейтілген бірінші жолды қосамыз.

(a11x1 + a12x2 + a13x3 + ... a1NxN = b1)*M +
a21x1 + a22x2 + a23x3 + ... a2NxN = b2

Аламыз

(a11*М + a21) x1 + ... = b1*M + b2

Х1мүшесі нөлге тең болу үшін M = -a21 ,a11 қажет. Бұл операцияны өткізіп, теңдеуді екінші теңдеудің орнына жазып, үшінші теңдеуге кірісеміз. Оған M = - a31 ,a11 көбейтілген бірінші теңдеуді қосып, x1 кезінде мүшенің орнына нөл аламыз. Мұндай операцияны барлық басқа теңдеулермен жасау керек. Нәтижесінде біз осындай жүйе аламыз:

a11x1 +
a12x2 +
a13x3 +
...
a1nxn = b1

a22x2 +
a23x3 +
...
a2nxn = b2

a32x2 +
a33x3 +
...
a3nxn = b3
...
...
...
...
...
аn1 ,х1
an2x2 +
an3x3 +
...
annxn = bn

Осыдан кейін x2 мүшелерінен үшінші, төртінші, N теңдеуінде құтыламыз. Ол үшін j нөмірімен теңдеуге M =-aj2 ,a22 көбейтілген 2-ші теңдеуді қосу қажет. Осы операцияны басқа теңдеулерден өткізіп, x2 -ден көп сандардағы теңдеулерде мүшелері жоқ жүйені аламыз.
Және олай бұдан әрі... Ол үшінші мүше үшін, Төртінші... теңдеу аяқталғанша, нәтижесінде үшбұрышты түр жүйесін аламыз.
Теңдеулер жүйесінен барлық белгісіз мәндерді табуға болады. Соңғы теңдеуден xn=bn(n-1) , ann(n-1) табамыз.
Соңғы теңдеуге xn қойып, xn-1 және т. б. табамыз, x1 -ге дейін ол белгілі болған кезде жүйенің бірінші теңдеуінен анықталады Xn,Xn-1, ..., X2
Осылайша, Гаусс әдісі бойынша бірінші кезеңде тура жүріспен деп аталатын бастапқы жүйе үшбұрышты матрицамен эквивалентті болып түрлендіріледі, ал екінші кезеңде кері жүріспен деп аталатын эквивалентті жүйені шеше отырып, беймәлім жүйені есептейді.

1.3 СТЖ Гаусс әдісімен шешу
Кез келген теңдеулер жүйесінде үш жағдай болуы мүмкін:
1.Жүйе үйлесімсіз:
2.Жүйе үйлесімді және анықталған:
3. Жүйе үйлесімді және анықталмаған:
Сызықты теңдеулер жүйесінің көптеген шешу әдістерінің арасында практикалық қолдануға және теориялық қорытындыларға да ыңғайлы әдістерінің бірі теңдеулер жүйесiндегi белгiсiздердi бiртiндеп жоюға негізделген Гаусс әдісі болып табылады. Қарапайым түрлендірулердің көмегімен берілген жүйе шешімдері айқын көрінетің түрге келтіріледі. Гаусс әдісі теңдеулердің кез келген жүйесіне қолданыла береді. Үйлесімсіз болады, егер түрлендіру процессінде 0*x1+*x2+...+0*xn= с, с!=0 (**) теңдеуін алсақ, басқа жағдайларда жүйе үйлесімді. Үйлесімді жүйе анықталған болады, егер ол үшбұрышты түрге келтірілсе ( r=n болған жағдайда) және анықталмаған, егер трапециялық түрге келтірілсе (rn жағдайында).

Кері матрицаның көмегімен сызықты теңдеулер жүйесін оңай шешуге болады. (1) жүйесін матрица түрінде жазсақ (1.1):

(1)

(1.1)

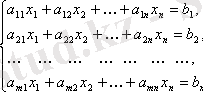
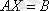
мұндағы

(1.2)

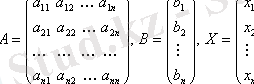
егер А- ерекше емес матрица болса, онда (1.2)

(1.3)

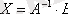
Сызықтық теңдеулер жүйесін Жордан - Гаусс әдісімен шешу.

Сызықтық теңдеулер жүйесі берілсін

(1)
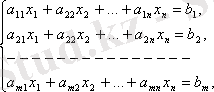
Осы жүйенің А матрицасынан 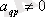элементін аламыз. Бұл элемент шешуші элемент деп, А матрицасының, р-ші тік жолдары - шешуші тік жолдар, Q-ші жатық жолдары- шешуші жатық жолдар деп аталады .

(1.1)

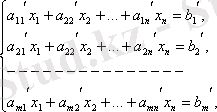
Жаңа теңдеулер жүйесін қарастырамыз. Бұл теңдеулер жүйесінің матрицасы A` болады, бұл жүйенің коэффициенттері мен бос мүшелері

(1.2)

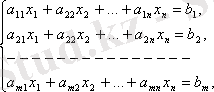
формулалардан анықталады. Дербес жағдайда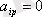, егер i !=q. Егерболса, (1.4)

(1.3)

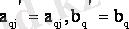
болады.
A` матрицаның 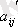элементін анықтау үшін "тіктөртбұрыш ережесін" қолданамыз. А матрицасының өзгеріске ұшырайтын 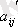элементін, 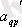шешуші элементін және 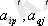элементін қарастырамыз. 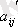элементін табу 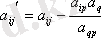формуласын қолданамыз. ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.