Векторлық көрсету әдістері

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 27 бет
Таңдаулыға:

Стереометриядағы векторлық əдіс

МАЗМҰНЫ

КІРІСПЕ . . . 3

1. ВЕКТОР ТҮСІНІГІ МЕН МӘНІ

1. 1. Вектордың тарихына шолу . . . 5

1. 2. Геометрияда вектор әдісмен теоремаларды дәлелдеу . . . 8

1. 3. Вектордың алгебрада қолданылуы . . . 15

2. СТЕРЕОМЕТРИЯДАҒЫ ВЕКТОРЛЫҚ ƏДІСТІҢ ҚҰРЫЛЫМЫ

2. 1. Векторлық көрсету әдістері . . . 19

2. 2. Векторларға қолданылатын сызықтық амалдар . . . 22

2. 3. Векторды координат өстердің орттары арқылы жіктеу. Вектордың

Модулі . . . 24

ҚОРЫТЫНДЫ . . . 29

ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . . 32

КІРІСПЕ

Курстық жұмыстың өзектілігі :XVIII-XX ғасырларда геометрияда жаңа әдістер пайда болды. Оларға жататындар: координаталық әдіс, геометриялық түрлендірулер әдісі, векторлық әдіс. Соның ішінде векторлық әдіс қазіргі уақытта зор табыспен қолданылып отыр. Сондықтан ғылыми жұмысымның негізгі мақсаты - векторлардың қолданылуы болып табылады. Ғылыми жұмыста негізгі қамтылған мәселелер де осы вектордың физикалық және геометриялық қолданысы мен оның өмірдегі маңызы және тарихына шолу жасау болып табылады.

Ғылыми жұмыстың негізгі бөлімінде векторларды пайдаланып шығарылатын геометриялық, алгебралық және физикалық есептермен танысамыз және геометриялық теоремаларды векторлық әдіспен дәлелдейміз. Соның нәтижесінде вектор тақырыбын терең игереміз және ғылымның күрделі, бірақ аса тартымды бастамаларымен танысамыз. Сондай-ақ векторлардың маңызы туралы қысқаша әңгімелеп береміз. Осы арқылы вектор жайлы толық мағлұмат аламыз.
Вектордың мектеп геометриясына да кіріп, орнығып алғанына көп уақыт болып қалды. Жаратылыстану-математика бағытында білім беретін мектептер бағдарламасында да векторларға көп уақыт бөледі. Векторларды мектеп бағдарламасына енгізбеу мүмкін емес еді, себебі вектор ұғымы - қазіргі заман ұғымдарының негізгі ұғымы.
Ғылыми жұмыстарымның нәтижесінде қазіргі математиканың негізгі әдістерінің бірі болып табылатын, техника ғылымдарында қуатты құрал болып табылатын векторлық әдісті меңгереміз.

Векторлар қолдануларға өте бай. Бірақ ең алдымен вектор дегеніміз не? Курстық жұмыс мақсаты : Вектор дегеніміз - өлшемімен ғана емес, бағытымен де сипатталатын және геометриялық қосу ережесіне бағынатын шамаларды айтамыз. Вектор латын сөзінен шыққан «ілестіру», «сүйреу», «тарту» деген мағынаны білдіреді. Сызбада вектор стрелкамен кескінделеді. Стрелка басынан ұшына қараған бағытын анықтайды. АВ векторының ұзындығын АВ векторының модулі немесе абсолют шамасы деп атайды және оны │ АВ │арқылы белгілейді.

Екі вектордың қосындысы вектор болады, ол қосындыны екі әдіспен табуға болады: бірі - үшбұрыш әдісі, екіншісі - параллелограмм әдісі.
Бұл біздің вектор туралы негізгі мәліметтеріміз. Ал қазір вектор жайлы көбірек айтуға және вектордың қолдануларына анағұрлым тереңірек мысалдарды, есептерді қарастырамыз.

Міндеттері:

1. Стереометриядағы векторлар әдісі туралы мәлімет жинау.

2. Стереометриядағы векторлар әдісі қасиеттерін қарастыру.

3. Курстық жұмысқа сәйкес есептерді шығру. .

Курстық жұмыстың құрылымы: Курстық жұмыс кіріспеден, екі бөлімнен тұрады. Кіріспеде курстық жұмыстың өзектілігі мен мақсаты көрсетілген. Бірінші бөлімде вектор түсінігі мен мәні қарастырылған. Екінші бөлімде стереометриядағы векторлық әдістің құрылымы қарастырылған, тақырып бойынша есептер шығарылды. Қорытынды жасалынды.

1. ВЕКТОР ТҮСІНІГІ МЕН МӘНІ

1. 1. Вектордың тарихына шолу

Векторлар техника ғылымдарының қауырт дамуына байланысты XVIII ғасырда бастау алып, XIX ғасырдың жартысында есептеудің талапқа сай жаңа түрін іздестіру барысында дүниеге келді. Векторлық есептеулердің жасы «жас» болғанымен бастау көзі сонау ерте заман данышпаны Аристотельдің «Механикалық проблемалар» атты еңбегінде кездеседі. Аристотель бұл еңбегінде бір нүктеге түсірілген және өзара бұрыш жасай бағытталған екі күштің әсерінен жүрген жолын табуды екінші мәселе етіп қойды.
XVIII ғасырда Аристотельдің «қозғалыстар параллелограмы» қайтадан жандана түсті. Галилео Галилей күш және оның денені қозғайтын құраушысының арасындағы метрикалық байланысты зерттеді. Оның еңбектеріне қарап, Галилейдің тең әсерлі күш, қорытқы жылдамдық ұғымдарына өте жақын, қапталдас келгенін көруге болады.
Ағылшын математигі, әрі физигі Исаак Ньютон қозғалыстарды жасауға алғаш рет «параллелограмм ережесін» пайдаланады. Неміс математигі Готфрид Вильгельм Лейбниц геометриялық есептеудің идеясын берді, бірақ дамытпады.
Механикадағы векторлық алгебраның негізін қалаушы Джон Валлис механикадағы геометриялық аппарат жасауға жаңа қадам жасады. Ол екі үш күштің әсерлі және қорытқы жылдамдығын анықтауға колданылатын «параллелограмм ережесін» берді. Күштерді, жылдамдықтарды қосу, жіктеу, векторларды санға көбейту амалдарын алғаш рет берген де осы адам. Сонымен векторлық алгебраның негізін қалаған оқымысты - Джон Валлис. Дәл осы бағытта аса табысты еңбек еткен Л. Карно. Ол «қозғалыстың геометриялық теориясын» жасау мәселесін көтеру және қазір пайдаланып отырған векторлық есептеудің символдық аппаратын жасап шықты.
Монж-Понселле мектебінің көрнекті өкілі Бара де Сен-Венан серпімділік теориясындағы, гидродинамикадағы, термодинамикада, жалпы механикадағы тамаша еңбектерімен физиктер мен механиктер арасындағы аса танымал тұлға еді. Сен-Венан векторлық есептеулер саласына қомақты үлес қосты, механикада қолданылатын векторлық аппаратты жетілдіруде жемісті еңбек етті. «О геометрических суммах и разностях их применения для упрощения механики» атты 1845 жылы жариялаған еңбегінде Сен-Венан скаляр көбейтінді, векторлық көбейтінді, векторлық фукцияны дифференциялдау, интегралдау ережелерін берді. Сөйтіп, ол механиканы вектор негізінде құрудың жалпы схемасын жасап шықты.

Понселенің шәкірті Резаль 1862 жылы жариялаған «Чистая кинематика» еңбегінде Сен-Венанның аппаратты жетілдіру және векторлық аппараттың кинематикада қолданылуларына толып жатқан мысалдар келтірді.
Д. Валлис, Л. Карно, Сен-Венан - бұлар векторлық алгебра және векторлық анализдің ұғымдарын ғылымға енгізді. Олар механикаға қажетті геометриялық аппарат жасау жолында жемісті еңбек етті. Бірақ векторлық есептеулердің негізін салушылар Ирландия математигі, астрономы Уильям Гамильтон және неміс физигі, математигі Герман Грассман деп айтылып жүр.
1844 жылы У. Гамильтон векторлық есептеулерге арналған алғашқы мақалалары және Г. Грассманның «Учение о претяженности» атты көлемді еңбегі жарияланды. 1853 жылы Гамильтонның «Лекции о кватерлонах» атты еңбегі жарық көрді. Бұлардың әрқайсысы есептеудің жаңа әрі әмбебап түрін жасады, векторлық есептеулерге көп еңбек сіңірді. «Вектор» ұғымын 1846 жылы ғылымға енгізген Гамильтон болды.

1. 2. Вектордың физикада қолданылуы

Вектор физикада, қолданбалы басқа да ғылымдарда қолданылады. Физикада вектордың көмегімен әр түрлі бағытталған шамалар: күш, үдеу, жылдамдық, т. б. өрнектеуге болады.

Вектордың физикадағы қолданысын білу үшін мына есепті қарастырайық.
Көлбеулік бұрышы болатын көлбеу жазықтықпен массасы m білеуше қозғалып келеді дейік. Білеушенің жазықтықпен үйкеліс коэффизиенті ν- ге тең.
Берілгені : m - масса, ν (ню) - үйкеліс коэффициенті, а - білеушесінің үдеуін табу керек.

Шешуі : Білеушеге үш күш әсер етеді: 1) ауырлық күші 2) тіректің реакция күші (байланыс күші) - ^ N ; 3) үйкеліс күші - F _үй .

Бұл суреттердің бағыттары суретте көрсетілген.

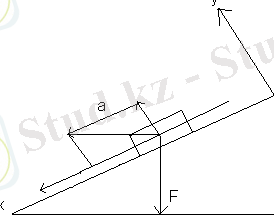
Осы күштер бірігіп, білеушеге оның бойымен төмен бағытталған а үдеу береді.
х пен у координаталар осьтерін сәйкес түрде көлбеу жазықтыққа параллель және оған перпендикуляр бағыттаймыз.

Ньютонның екінші заңын векторлық әдіспен былай жазамыз: ma = mg + N+F _үй . Ал бұл теңдеуді скаляр түрінде жазу үшін, векторлардың х пен у осьтеріндегі проекцияларын табайық.

х осіндегі проекциядан бастайық.

аүдеу векторыныңхосіндегі проекциясы оң (ах) жәнеавекторының модуліне тең (авекторыхосьіне параллель) ах=а.
- ауырлық күшін құраушыларға жіктейміз. Тіктөртбұрыш шығады. Олардың қабырғалары-ның құраушылары.
проекциясыхосіндегі ∆ABD-дан(Fа) = sin; оңхосімен бағыттас.
Үйкеліс күші векторлық проекциясы теріс және -Fүй-ке тең.
Тіректің реакция күшінің (байланыс күшінің) векторының проекциясы нөлге тең. Өйткені ол векторхосіне перпендикуляр. . Ньютонның екінші заңыхосіндегі векторлардың модульдері арқылы өрнектелген, сондықтан проекциялар үшін теңдеуінің түрі мынадай:Fүй(2) Ендіуосіндегі проекцияларды табамыз:

1) Үдеу векторының у осіндегі проекциясы нөлге тең. ( а векторы у осіне перпендикуляр)

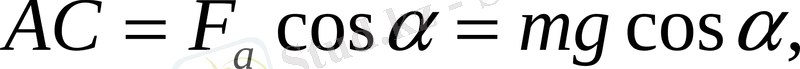2) АСD -дан күшінің проекциясы мынаған тең болатынын көруге болады: =cos . Осыдан шығатыны: теріс

3) Тіректің реакциясы күші векторының проекциясы оң және оның модуліне тең:

4) Үйкеліс күшінің векторының проекциясы нөлге тең F _үй = 0.

Бұл жағдайда Ньютонның екінші заңының теңдеуі мына түрде жазылады: 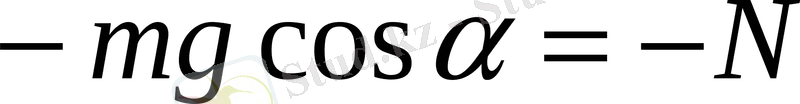яғни, , Үйкеліс күші F _үй = νN тең екенін білеміз.

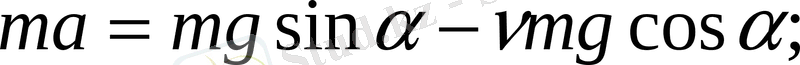
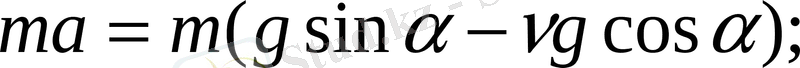
F _үй = νmg cos екінші формулаға қоямыз. 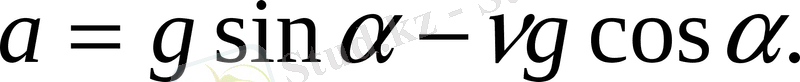Осы формуладан еркін түсу үдеуінен кем екенін көріп отырмыз. Егер үйкеліс болса ( ), онда көлбеу жазықтық бойымен сырғанап келе жатқан дененің үдеуі модулі жағынан яғни мұнда да, ол g -ден кем.

Векторлар көлбеу жазықтыққа кең түрде пайдаланылады, себебі олар төмен түскенде не жоғары көтерілгенде үдеуі кемітуге мүмкіндік жасайды.

1. 2. Геометрияда вектор әдісмен теоремаларды дәлелдеу

Вектор геометрияда көптеп қолданылады. Вектор ұғымының геометрияда қолданылуы кейбір күрделі геометриялық ұғымдарды ықшамды айтуға, геометриялық есептерді шығарудың ерекше бір әдісін табуға мүмкіндік берді. Векторлық әдістің геометрияда қолданылуын екі топқа бөлуге болады. 1) Векторлық амалдарды оқып-үйрену барысында геометриялық фигуралардың және оның қасиеттерін колдана отырып шығарылатын есептер. 2) Геометрияда вектор әдісмен теоремаларды дәлелдеу.
Мысалы, векторлық әдіспен үшбұрыштың орта сызығы туралы теораманы дәлелдеуге болады.

Теорема: Үшбұрыштың орта сызығы үшбұрыштың табанына параллель және оның жартысына тең.

Берілгені: АВС , МК орта сызығы. Дәлелдеу керек:

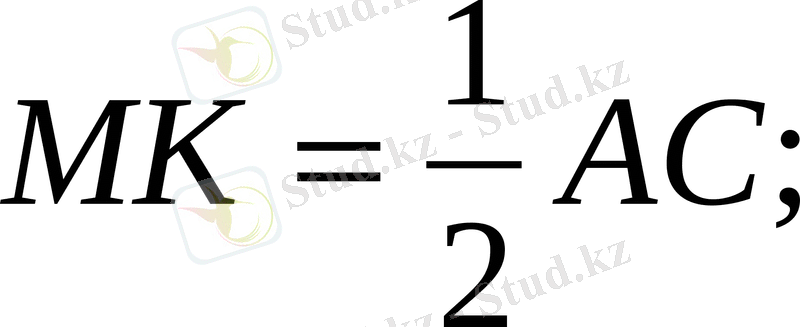
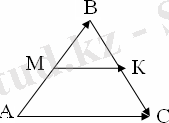
Дәлелдеуі: 1) АВ = с , ВС = а , АС = b

Вектордың қосындысының анықтамасы бойынша:

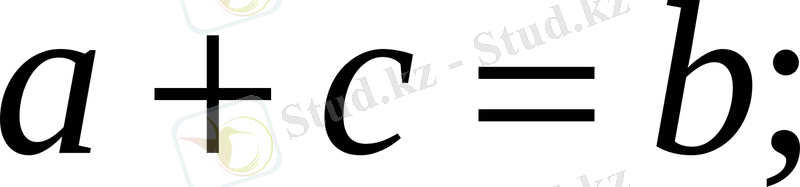
М және К нүктелері АВС -ның АВ және ВС қабырғаларының ортасы.

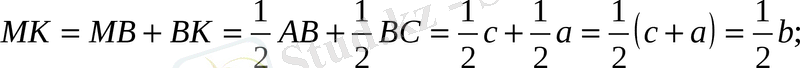
онда

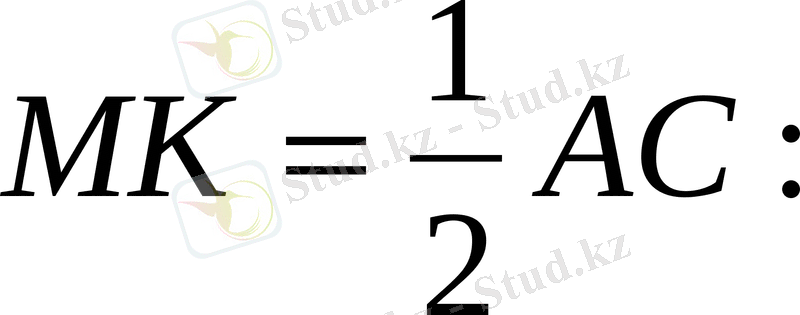
Теорема дәлелденді.

Сонымен қатар ромбының диагональдары перпендикуляр екенін де вектор әдісі арқылы оңай дәлелдеуге болады.

Теорема: Ромбының диагональдары тік бұрыш жасап қилысады.

Б 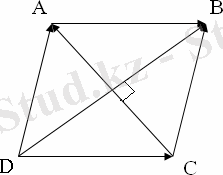ерілгені: ABCD - ромб. BD және AC - диагональдар. Дәлелдеу керек:

Дәлелдеуі: 1. Мынадай белгілеулер енгізейік.

АВ=а , ВС=b ромбының анықтамасынан

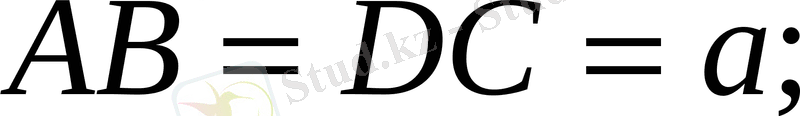
2. Векторлардың айырмасымен қосындысынан шығатыны:

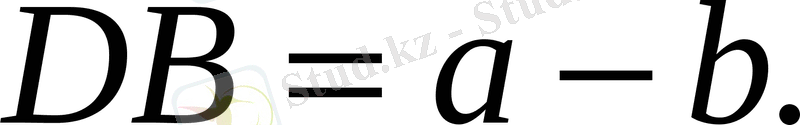
3. скаляр көбейтіндінің қасиеті бойынша.

4. Ромбының қабырғалары тең болғандықтан 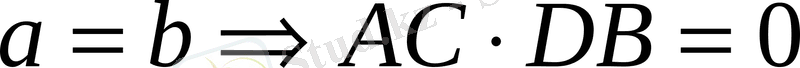олай болса,

Векторлық қасиет геометрияда кейбір кесінділердің параллельдігін дәлелдеуде қолданылады. Мұндай жағдайда есептерді шығарғанда, векторлардың коллинеарлығы қолданылады.

^ Мысалы : Жазықтықта ABCD төртбұрышы және одан тыс жатқан М нүктесі берілген. М нүктесіне АВСD төртбұрыштың АВ , СD , ВС , DА қабырғаларының ортасына қарағанда симметриялы нүктелер параллелограмның төбесі болатындығын дәлелдеу керек.

Б 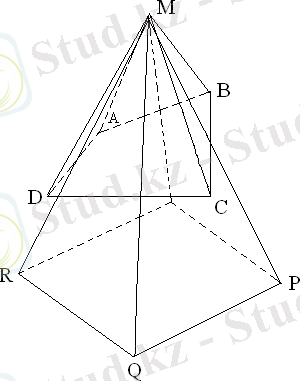ерілгені: АВСD - төртбұрыш. R , N , P , Q - M нүктесіне АВ , ВС , СD және DА кесіндісінің ортасына қарағанда симметриялы нүктелер.

Дәлелдеу керек:

RNQP - параллелограмм.

Дәлелдеуі: Параллелограмм ережесі бойынша: MN = MA + MB ; MP = MB + MC ; MQ = MC + MD ; MR = MD + MA . (1)

Вектордың айырмасының анықтамасы бойынша: NR = MR - MN және PQ = MQ - MP ; NR - PQ =( MR - MN ) -( MQ - MP ) болғандықтан (1) теңдіктен NR - PQ =0 болады.

NR = PQ сол сияқты NP = RQ , бұдан шығатыны NR = PQ және NP = RQ , яғни NPQR - параллелограмм.

Вектордың қолданылуының тағы бір түрі: нүктенің кесіндінің ортасы немесе кесіндіні белгілі бір қатынаста бөлетіндігіне байланысты есептер.

М 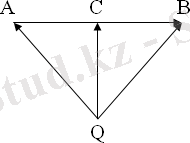ысалы : С нүктесі АВ кесіндісін АС : СВ = m : n бөлетіндігін дәлелдеу үшін: 1)

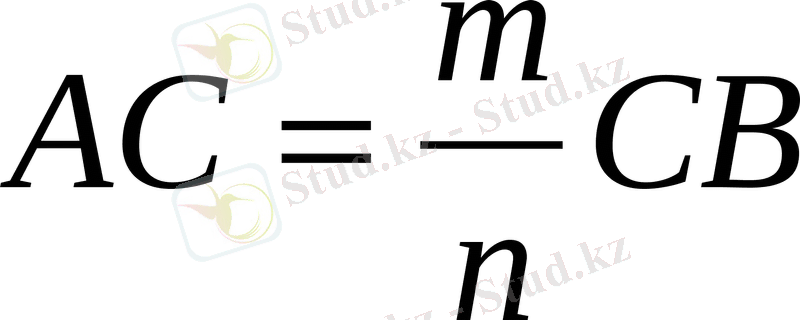
2) ( Q - кез-келген нүкте) болатындығын дәлелдесек жеткілікті.

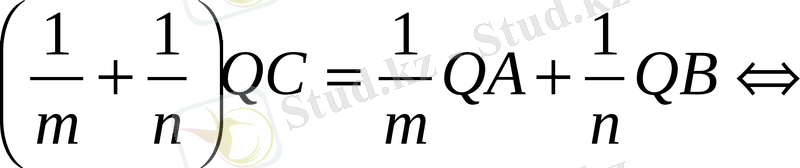
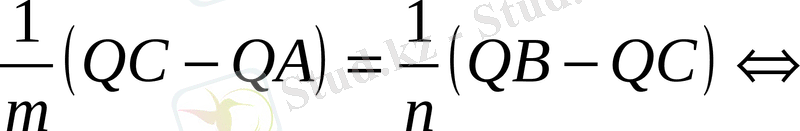
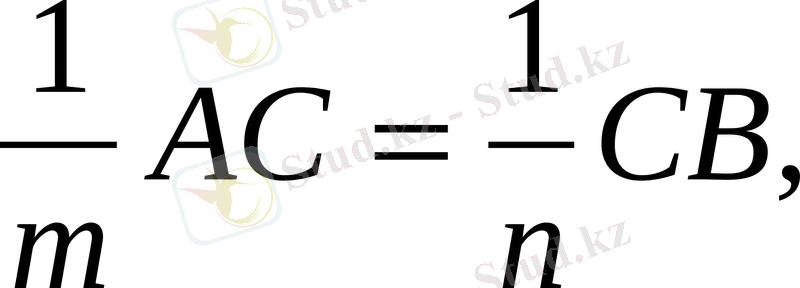
Векторлардың скаляр көбейтіндісінің қасиетін қолданып, кез-келген үшбұрыштың биіктіктері бір нүктеде қилысатынын дәлеледеуге болады

Д 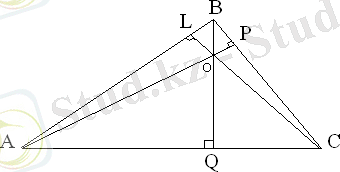әлелдеу керек: АР ВС ; ВQ CA .

1. AP және BQ - АВС -тың биіктіктері, О - олардың қилысу нүктесі.

2. ОА = а ; ОВ = в ; ОС = с ;

L нүктесі ОС мен AВ -ның қиылысуы.

3. Векторлардың айырмасы-ның анықтамасына сүйеніп, АВ = в - а ; ВС = с - в ; СА = а - с ;
4. РА ВС , онда

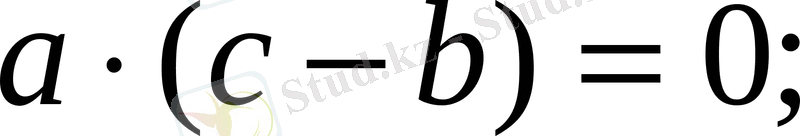
5. Осы сияқты ОВ СА болғандықтан яғни,

6. Бұл теңдіктерден шығатыны ОС АВ .

7. Яғни, СL - ABC -ның биіктігі.

1. 3. Вектордың алгебрада қолданылуы

Вектор ұғымы - физикалық ұғым ғана емес, математикалық ұғым. Математикада еркін вектор ұғымы қолданылады. Векторларға қолданылатын амалдардың ішінде байы - скаляр көбейтінді амалы. Ол алгебрада теңсіздіктерді, теңдеулерді, теңдеулер жүйесін шешуде қолданылады.

Екі вектордың скаляр көбейтіндісі олардың абсолют шамаларын олардың арасындағы бұрыштың косинусына көбейткенге тең болады.

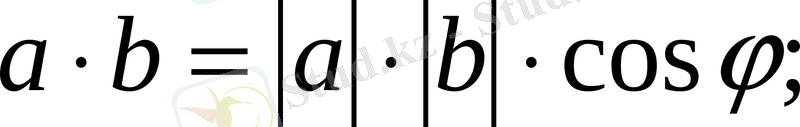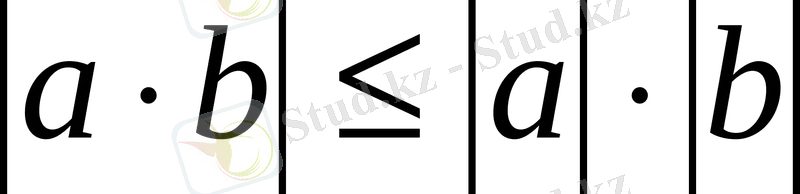; ал соs 1 онда (1)

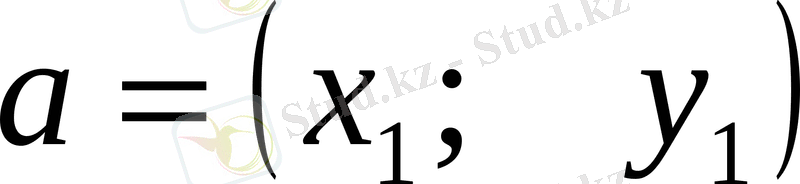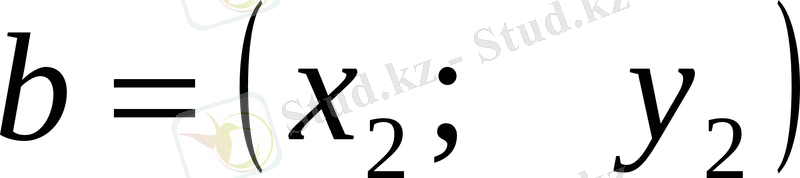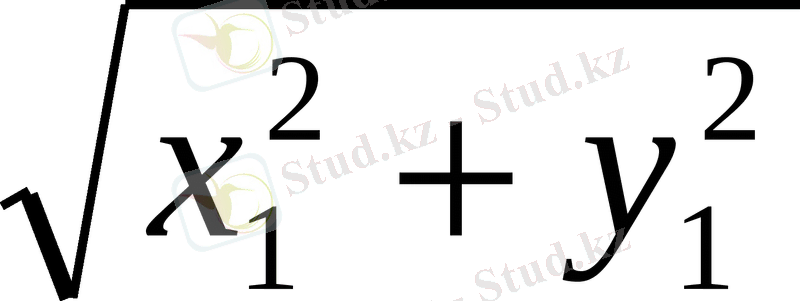
Сондықтан егер және векторлары берілсе, онда = = 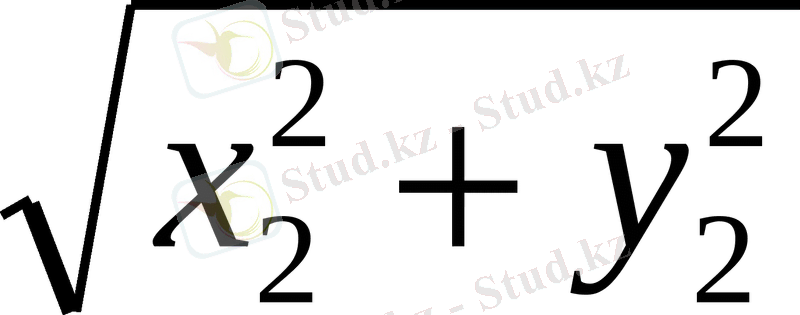(2)

Ал үш өлшемді кеңістікте: 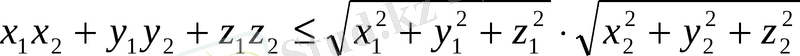(3)

Мысалы: онда 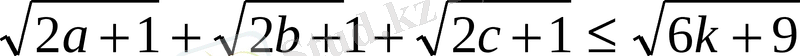дәлелдеу керек.

Дәлелдеуі: х және у векторлар берілген болсын. Оның координаталары

х ( 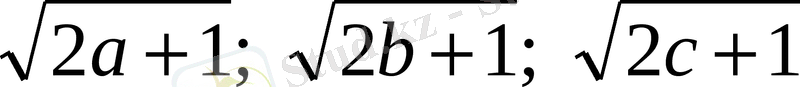) ; у (1; 1; 1) . (3) формула бойынша

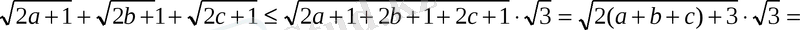
2. Кейбір теңсіздікді дәстүрлі әдіспен дәлелдеу қиынға түседі. Векторлық әдісті қолдану есепті шешуді жеңілдетеді және тездетеді.

Мысалы :

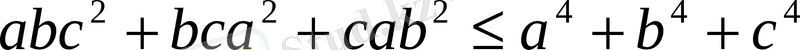
Мынадай векторларды қарастырайық.

х ( ас ; bа ; сb ) ; у ( bс ; са ; аb ), бұдан ;

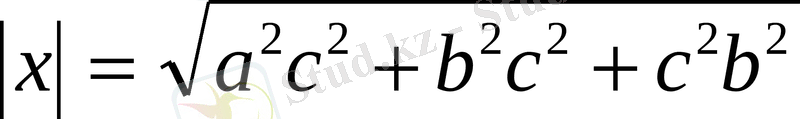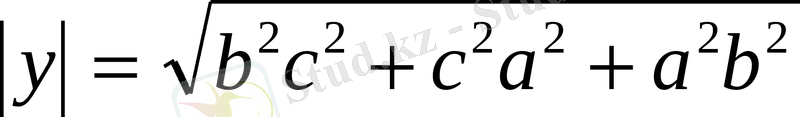
Формула бойынша:

=

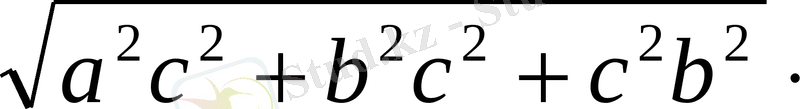
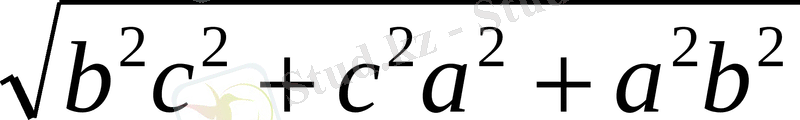
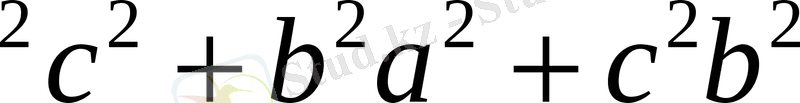
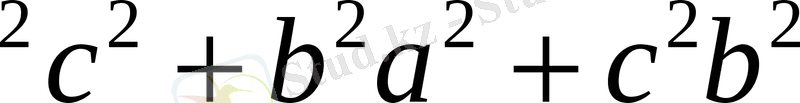
Енді х ( а ², b ², с ²), у ( с ², b ², а ²) болсын. Теңсіздіктің оң жағына формула қолдансақ, 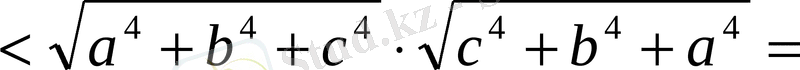шығады, олай болса, теңсіздік дәлелденді.

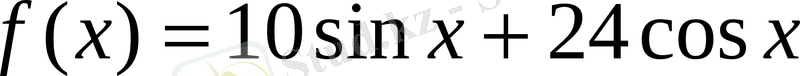функциясының максимум және минимум мәнін табу керек болсын.

Алгебралық өрнекті а және b векторларының скаляр көбейтіндісі деп қарастырсақ, онда а (10; 24) және b (sin x ; cos x ) болады.

.

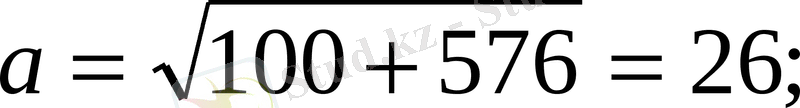
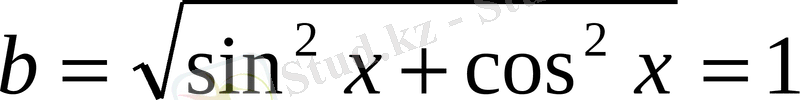Скаляр көбейтіндісінің қасиетіне сүйенсек, 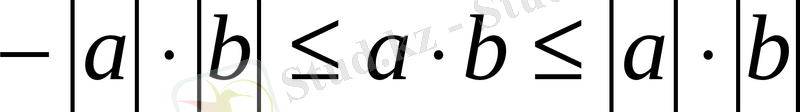болғандықтан, болады. Сонда min f ( х ) =-26, max f ( х ) =26.

4. Теңдеулер жүйесін шешу.

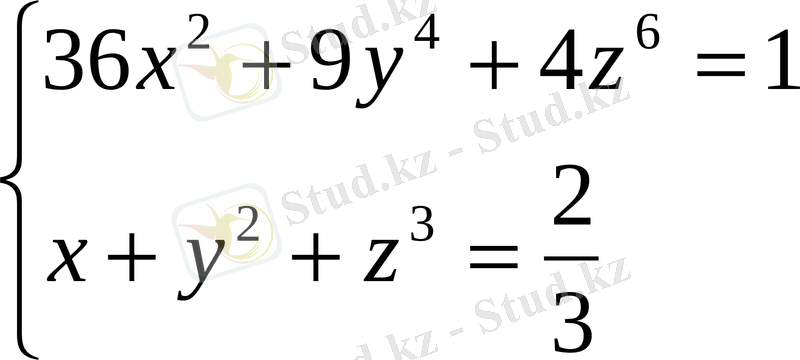
теңдеулер жүйесін шешу үшін мынадай векторларды қарастырайық: 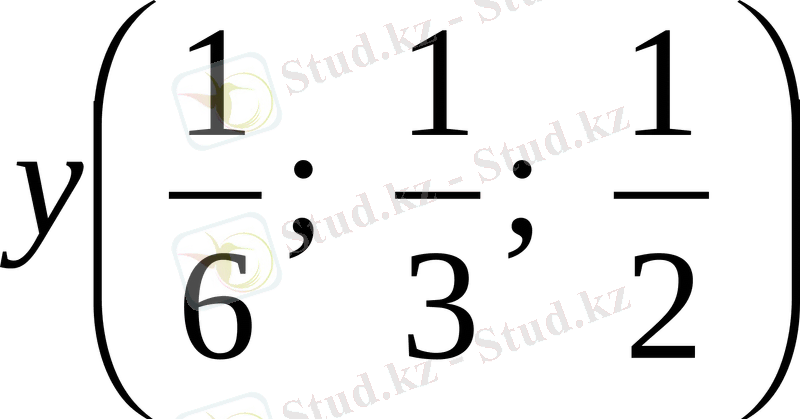ұзындықтарын табамыз.

,

=

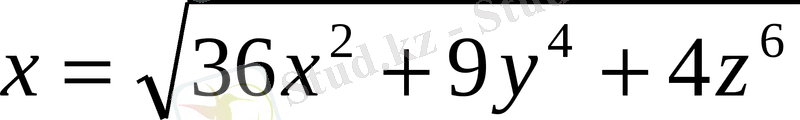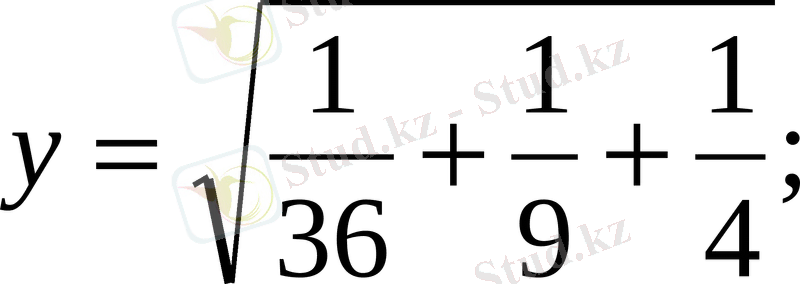
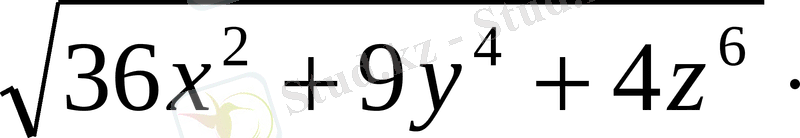
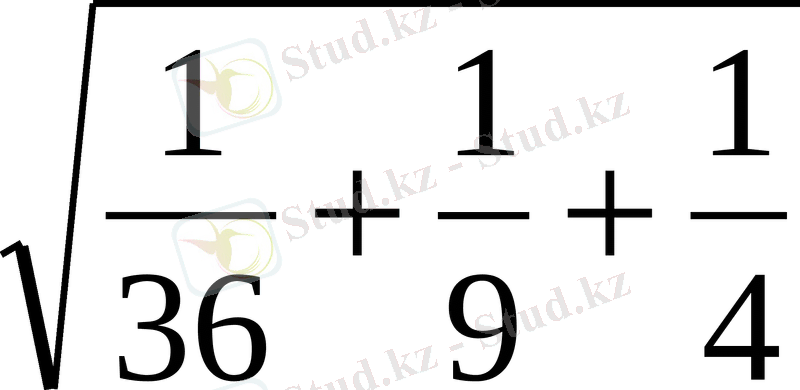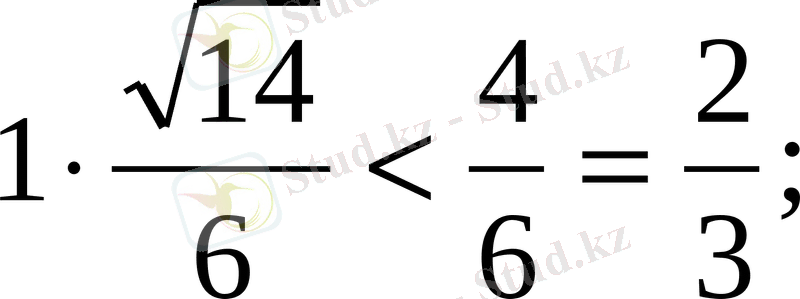
Ал, 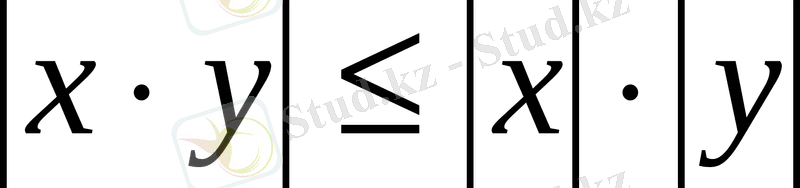болғандықтан жүйенің шешімі болмайды.

2007 жылғы олимпиадалық мына есепті: 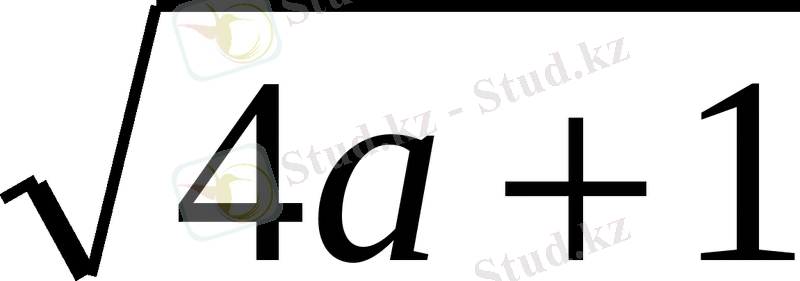+ + 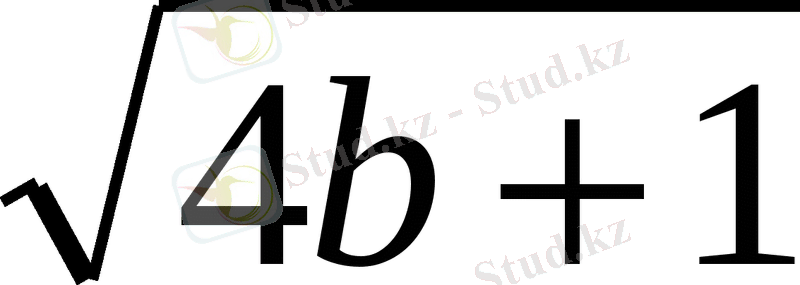векторлық әдісті пайдалана отырып шығаруға болады:

Шешуі :

a + b + c =1

p =(1; 1; 1) және q =( ; ; )

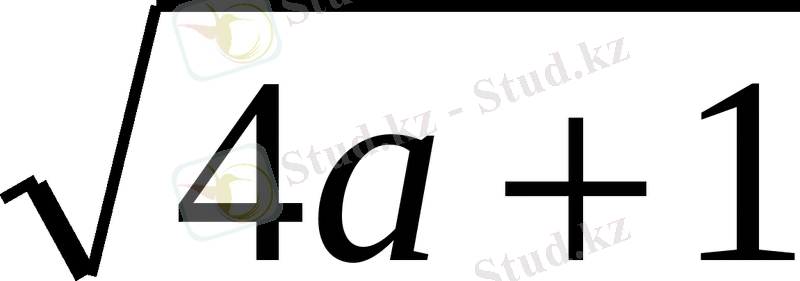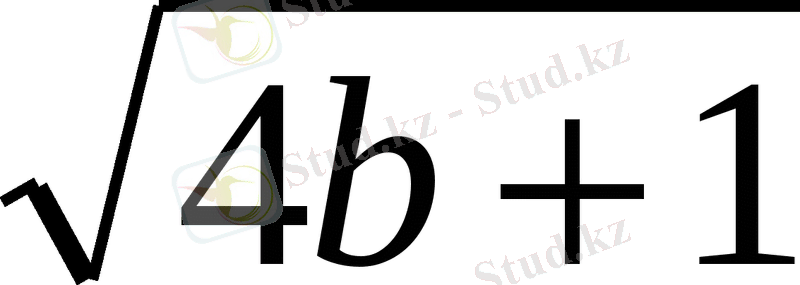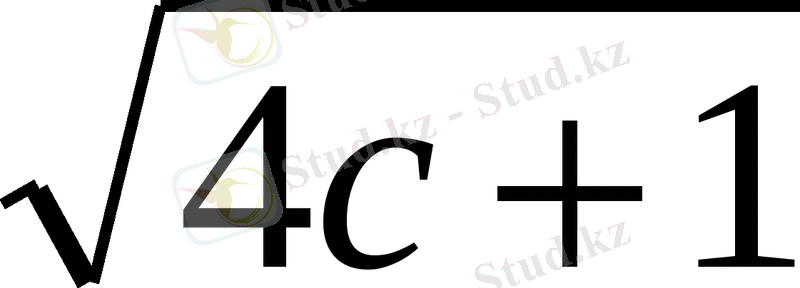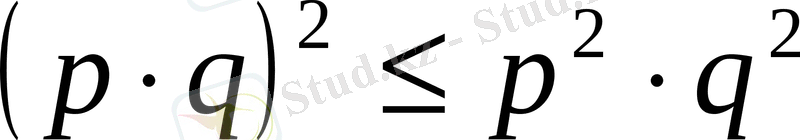немесе

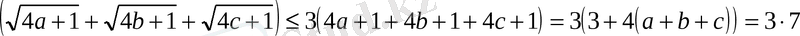
a + b + c =1 болғандықтан, 3(3+4⋅1) =21. Теңсіздік дәлелденді.

Осы тәрізді вектор әдісі арқылы шығарылатын бірнеше мысалдар келтіруге болады.

1-есеп: күрделі иррационал теңдеуді вектордың көмегімен шешуге болады.

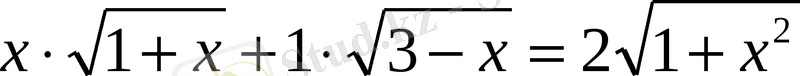теңдеуін қарастырайық.

Шешуі : екі вектор 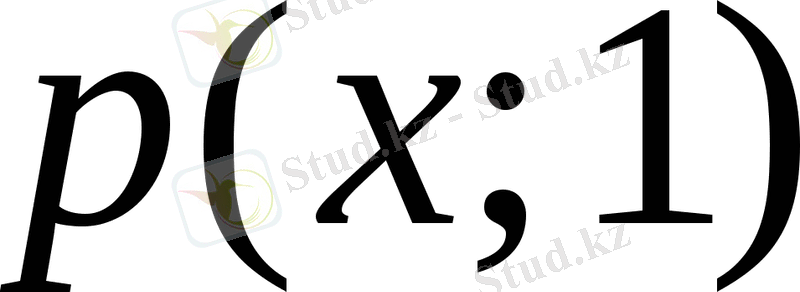және 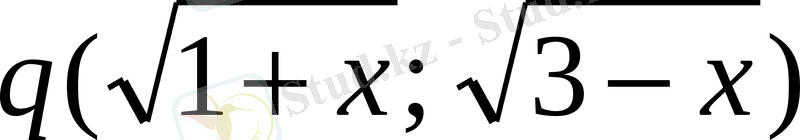. Осы векторлардың скаляр көбейтіндісі

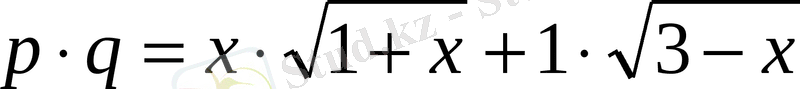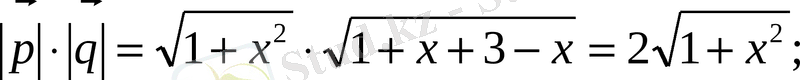
модульдерінің көбейтіндісі анықтама бойынша векторлар коллинеар (бағыттас) болады.

⇒ ⇒

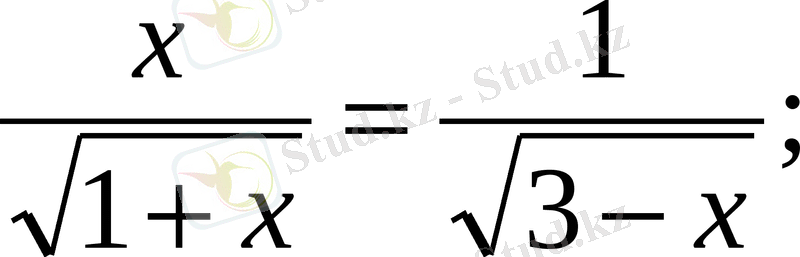
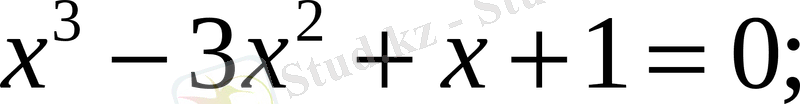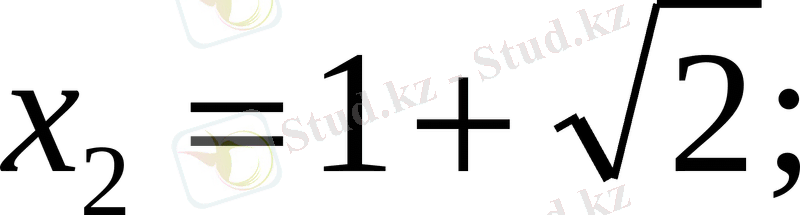
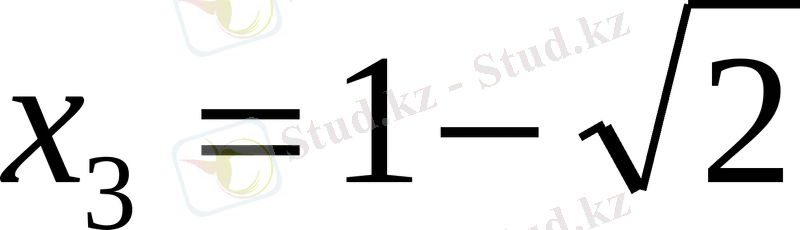
Жауабы: .

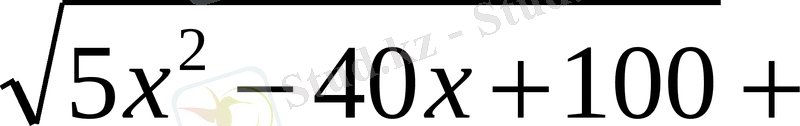
2-есеп: Кез-келген х саны үшін 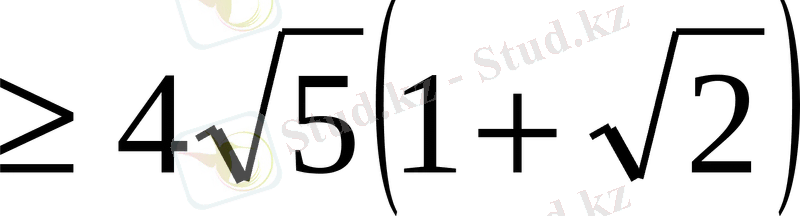(1) теңсіздігін дәлелдеу керек. Теңдік белгісі қандай жағдайда орындалады?

Шешуі : (1) теңсіздіктің екі жағын да -ке көбейтіп, жазсақ:

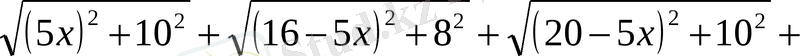
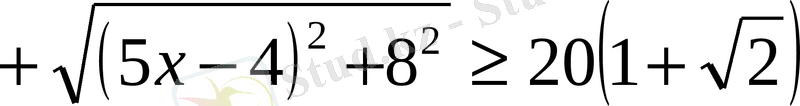(2)

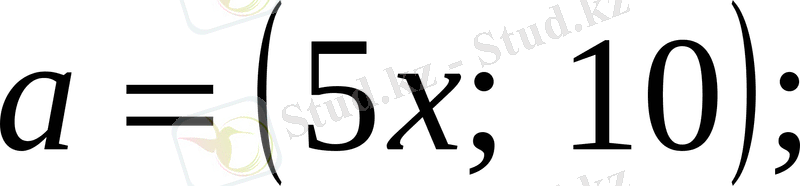
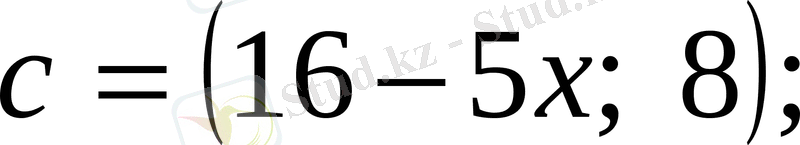
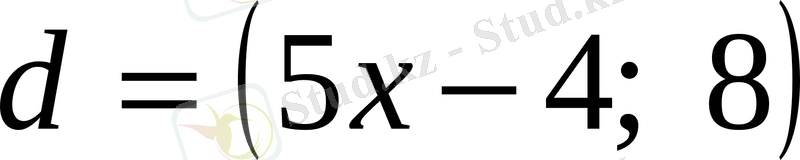векторларын қарастырайық. Бұдан шығатыны:

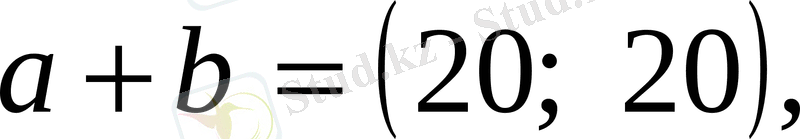
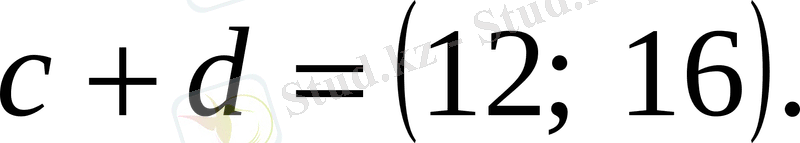
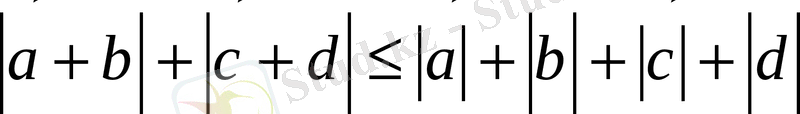сүйеніп, (3) -тен (2) -ні алып, оның екі жағын да санына бөліп жіберіп, (1) теңсіздікті аламыз.

«=» белгісі мен және мен векторлары бағыттас болғанда, яғни

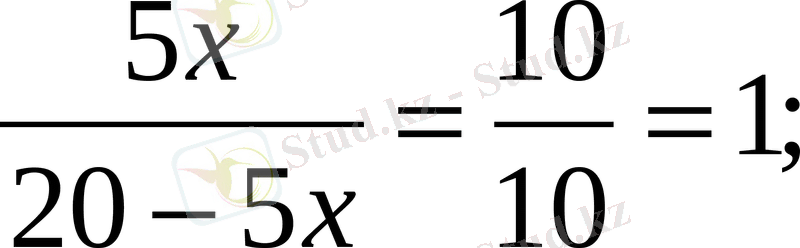
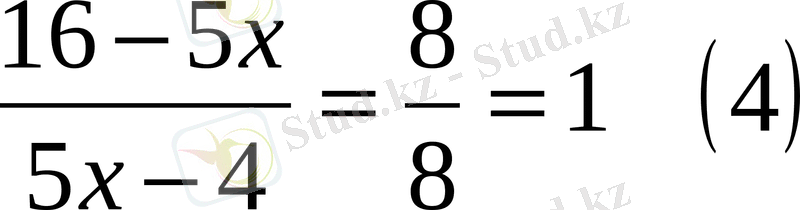шарттары орындалғанда ғана орындалады. (4) -ті шешіп, екендігі шығады. Теңдік болғанда орындалады.

Векторлар ғылым мен техниканың көптеген салаларында маңызды рөл атқарып, есептердің алуан түрлерін шығаруда үлкен қолданысқа ие болып отыр. Мысалы, векторлар теориялық физикада, математикалық физикада, теориялық механикада, аэродинамикада, гидродинамикада, өрістер теориясында, электротехникада тағы басқа ғылыми салаларында қолданылады. Осыдан векторлық әдісті игерудің қаншалықты маңызды екендігін көрдік. Солардың негізгілерін тағы да атап өтелік.

Векторлар табиғат құбылыстарын зерттеуге қолданылады. Физиканың бірталай заңдары «вектор» тілінде өрнектеледі. Векторларды қолдану математиканы физикамен байланыстыруға, математиканы физикалық мазмұнды есептермен байытуға мүмкіндік берді.
Векторлық аппаратты геометриялық есептерге қолданғанда қазіргі заманға сай әдістеме, оның идеяларын зерттеу әдістері туралы түсінік беруге мүмкіндік туады.
Компьютерлік техникада, сызықтық программалау есептерінде, халық экономикасына байланысты есептерді шешуге қолданылады.
Векторлық әдісті пайдалану физика, информатика, астрономия және есептеуіш техника сияқты математикамен сабақтас бағыттарды жеңіл меңгеруге игі әсер етеді.
Астрономия және басқада карталарды кескіндеуге үлесі көп.
Ең бастысы есеп шығаруда маңызды қызмет атқарады. Ылғида болмаса да векторлық әдіспен теңдеулердің, теңдеулер жүйесінің, теңсіздіктің кейбір түрлерін векторлық әдіспен шешуге болады.

Сондықтан, есеп шығаруда, геометриялық есептерді шешуде векторлық әдісті қолдануға болады.

2007 жылы облыстық олимпиадада болған мына есепт де вектордың көмегімен шешуге болады:

Егер а + b + с =1 болса, онда 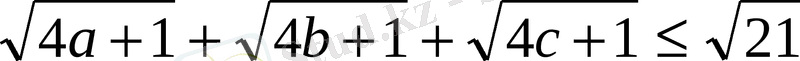теңсіздігін дәлелде.

Сонымен Қатар мына есептепді вектор әдісімен шешуге болады.

1) Егер х + у + z =1 болса, онда 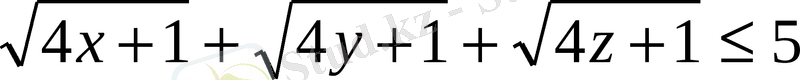теңсіздігін дәлелде.

2) 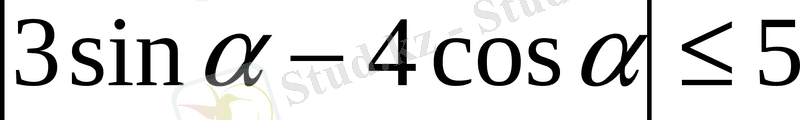теңсіздіктің α -нің кез-келген мәнінде орындалатындығын дәлелде.

3)

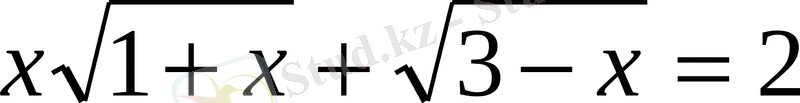
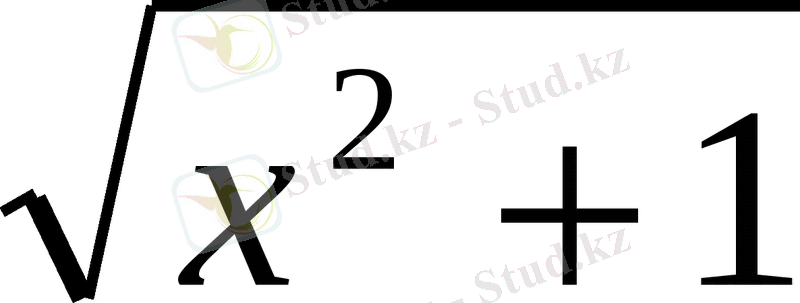
4)

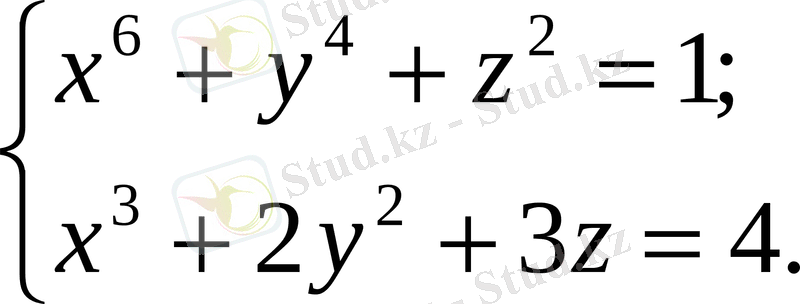
Бұл векторлық әдістің қолдануға бай екендігін көрсетеді.

2. СТЕРЕОМЕТРИЯДАҒЫ ВЕКТОРЛЫҚ ƏДІСТІҢ ҚҰРЫЛЫМЫ

2. 1. Векторлық көрсету әдістері

Векторлық көрсету (vektor data structure, vektor data model) - синонимі; деректердің векторлық моделі-қос координаттардың жиынтығы түріндегі нүктелік, сызықтық жəне полигональды кеңістік объектілердің асандық көрінуі. Олар тек объектілердің геометриясын ғана сипаттайды, бұл сызықты жəне полигональды кеңістік объектілердің сандық көрінуі. Олар тек объектілердің геометриясын ғана сипаттайды, бұл сызықты жəне полигональды объектілердің топологиялық, векторлық көрінуіне немесе векторлы-топологиялық, векторлы-топологиялық көріну түріндегі геометрия мен топологиялық қатынасқа (топологияға) сəйкес келеді; машиналық жүзеге асыруда векторлық көрінуге кеңістік мəліметтердің векторлық көрінуге кеңістік мəліметтердің векторлқ форматы vektor data format, деректердің векторлық құрылымы кортографиялық объектілердің геометриясын ғана көрсетеді. Оған пайдалылықты қосу үшін, геометриялық деректерді жеке файлда немесе деректер базасында сақталатын сəйкес келетін атрибутивті деректермен байланыстыру қажет. Осының арқасында объектілердің жиілікті көрінуі картаға көп ұқсас болады. Растрлы құрылымда əрбір ячейкаға антрибуттың мəні жазылады. Векторлықта мүлде басқа əдіс пайдаланылады, яғни нақты түрдегі антрибурсыз өзіндік графикалық примитивті сақтайды жəне жеке антрибутивті деректер базаларна сүйенеді. Деректердің векторлық құрлымдарда сызық жəне одан көп координаттардан тұрады. 1 қима үшін кеңістікте жағдай мен бағыт беретін координатттардың 2-еуі жеткілікті. Одан, күрделі сызқтар қималардан тұрады, олардың əрқайсысы қос координатпен басталып, аяқталады. Қисық сызықтар үшін қысқа түзу қималардың үлкен санының көмегімен болжамды көріністер пайдаланылуы мүмкін қималар кескінділер қысқа болған сайын олар барынша нақты күрделі сызықты көрсетеді. Сөйтіп, деректердің векторлық құрылымды кеңістікке объектілердің жағдайын жақсы көрсетсе де, олар нақты емес. Олар сонда да географиялық кеңістікке шамалап алынған бейнесі болып табылады. Кейбір сызықтар өздігінен болып жəне белгілі бір антрибутивті ақпаратты ақпараттарды иеленсе, басқалары торат деп аталатын сызықтың күрделі түрі, ол осы сызықтардың кеңістік қатынастары туралы қосымша ақпаратты да құрайды. Мысалы, жолдық торап жолдың типі туралы ақпаратты ғана емес, сол сияқты ол қозғалыстың мүмкін болатын бағытын көрсетеді. Бұл ақпарат əрбір кеңістігіне тəн болуы қажет, өйткені тұтынушыларға қозғалыс əрбір кесіндінің бойынан, антрибуттардың өзгеруіне дейін, тіпті екі жақты көше, бір жақты болғанға дейін жалғасуы мүмкін екендігін ескертеді. Осы кесінділерді байланыстыратын басқа кодтар, оларды біріктіретін түінділер туралы ақпаратты қосулары мүмкін. Түйін, мысалы, тоқтау белгісін, бағдаршам немесе бұрылуға болмайды деген белгіні иеленуі мүмкін. Барлық осы қосымша антибруттар барлық торап бойнша анықталуы керек, компьютерге осы тораппен үлгіленетін қатынастың жүзеге асырылатындығын ескертеді. Байланыстылық жəне кеңістік қатынастар туралы мұндай нақты ақпарат топология деп аталады. Аудандық объктілер сызықтыққа ұқсас деректердің векторлы құрылымында көрсетілуі мүмкін. Бірнші кесіндінің координатының бірінші 2-і, біруақытта болып табылатын сызық кесінділерін тұйық түйінге біркітіре отырып область немесе полигон құрылады. Нүктелер мен сызықтар сияқты, полигондармен де объектілердің атрибуттарын құрайтын файл байланысады. Полигон (polygon, area, area feature, region, face) - синонимі көп бұрыш, полигональды объект, контур, контурлы объект, облыс, кеңістік объектілердің негізгі 4 типінің бірі, векторлы-топологиялық көрінулерде немесе «спагетти» моделіндегі сегменттерде тұйық доға түрінде пайда болған жəне ішкі нүктелермен ұштасқан, олардың атрибуттар мəнінде ұйымдасқан, ішкі облыс; ішкі полигондарды (innex poligon) құрамайтын қарапайым полигон (simple poligon) мен «аралдар» (island) жəне анклавтар (hole) деп те аталатын ішкі полигондарды құрайтын құрылымдық полигон (complex poligon) деп бөлінеді.

Полигондардың бірігіуі ерекше ұштасатын полигондарды қосатын стандарта универсалды полигон (universe fase) немесе көрсетілген территрияның шекарасында сыртқы облыс (outside) деп аталатын қабаттың басқа да барлық полигонына қатынасы бойынша сыртқы полигнальды қабатты түзеді.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.