Сөйлемдер мен пікірлер

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 18 бет
Таңдаулыға:

№ 3 Ә. Молдағұлова атындағы жалпы орта мектебі

" Мектеп шеңберіндегі математикалық логика есептері "

" Мектеп шеңберіндегі математикалық логика есептері "
ғылыми жобасына
ПІКІР

Бұл жоба оқушылардың логикалық ойлау қабілетін дамытатын маңызды тақырыптарының бірі.
Алгебра курсында қарастырылатын Логикалық есептерді шешу жолдарының әр түрлі әдістеріне негізделіп отыр.
Ұсынылған жобаның басты мақсаты логикалық есептерді тез, әрі тиімді шешуге бағытталған. Логикалық есептерді шешудің тиімді тәсілдері арқылы оқушылардың тез түсініп, жылдам шығарылуын көрсетті.
Автор ұсынылып отырған материалдарға жан-жақты талдау жасап, терең зерттеген. Пайдаланылаған әдебиеттер тізімін көрсете отырып, көп іздену жұмыстары жүргізілгені көрінеді. Мен бұл жұмысқа өте жоғары баға беремін.

Аннотация
Зерттеудің мақсаты:
1. Логикалық есептердің түрлері, оларды шешу, әртүрлі тәсілдермен тиімді шығару.
Зерттеудің жаңалығы :
1. Логикалық есептердің ерекшеліктерін ашып ,айқындау.
Зерттеудің әдістері:
Кітапханаларда арнайы зерттеу жұмыстар жүргізу, ғаламтордан , тарихи зерттеп ой-пікірлерді, түрлі басылымдарды, оқулықтардан логикаға қатысты мәліметтерді бір жерге жинақтап, топтастыру, оқушылармен сауалнама жүргізу, нәтижесін табу.
Зерттеудің нәтижесі:
Оқушылар логикалық есептің мағынасын түсініп,тез шығаратын болды.

Кіріспе
Білім өркениеттіліктің әрі өлшемі, әрі тетігі болып табылатындықтан кез келген мемлекеттің рухани және әлеуметтік дәрежесі білім деңгейіне байланысты бағаланады.
Жан-жақты үйлесімді, өркениетті елдің ұрпағын тәрбиелеп шығу бүгінгі мектептің алдына қойылған мақсаттардың бірі. Бүгінгі заман талабына сай оқыту әдістемесін күннен күнге жетілдіре түсуін талап етеді. Осы талаптың орындалуы орта мектеп бағдарламасындағы әрбір пәннің әр тарауының әр тақырыбын оқушы санасына жететіндей етіп оқытқанда ғана орындалады. Олай болса, оқушыларды жеке тұлға етіп тәрбиелеуде математика пәнінің де алатын орны, салмағы зор.
"Математикалық логика дегеніміз не?" деген сауалға сай келетінін жасуапты бір сөзбен мынадай қалыптама түрінде беруге болатын секілді:
Математикалық логика = математикаланған логика + логикаланған математика.
Бұл жоба жұмыстың мақсаты: мектеп қабырғасында оқытылатын математикалық логика элементтерінің кейбір тұстарын нақтылап, мысалдар келтіру арқылы айқындап көрсету.
Логикалық есептер мектептегі алгебра курсының маңызды тақырыптарының бірі. Егердеосы логикалық есептерді шешудің оңай тәсілін оқушылар меңгеретін болса, онда есеп шығару барысында қиналмай тез шығарады.

I. Математикалық логиканың элементтері

1.1. Сөйлемдер мен пікірлер

Қоршаған ортаны танып білу барысында адамдар объектілердің арасындағы, объектілер мен олардың қасиеттерінің арасындағы өзара байланысты анықтайды. Осы байланыс түрлі ұғымдардан құралған сөйлемдер арқылы беріледі. Мысалы, "Тең қабырғалы үшбұрыштың барлық бұрыштары тең", "28 саны 7 - ге бөлінеді", "16 жұп сан".
Әрбір математикалық сөйлем өзінің мағынасымен және логикалық құрылымымен сипатталады. Сондықтан біз сөйлемнің құрылымына ерекше көңіл бөлеміз. Математикада сөйлемдер жәй (элементар) және құрама (күрделі) болып бөлінеді. "28 саны 7 - ге бөлінеді" деген сөйлем жәй. "28 саны жұп және 7 - ге бөлінеді 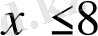", "" , "Егер үшбұрыш теңбүйірлі болса, онда оның табанындағы бұрыштары тең" сөйлемдері құрама сөйлемдер.
Құрама сөйлемдер жәй сөйлемдер "және", "немесе", "егер", "онда", "емес" деген сөздермен байланыстыру арқылы жасалады. Бұл сөздер математикада логикалық жалғаулар деп аталады.
Құрама сөйлемнің логикалық құрылымын анықтау үшін
1. Берілген құрама сөйлем қандай жәй сөйлемдерден құралған;
2. Қандай логикалық жалғаулармен байланысқан екенін білу керек?
Мысалы, "28 саны жұп және 7 - ге бөлінеді" деген сөйлемнің логикалық құрылымын анықтайық. Ол мынадай екі жәй сөйлемнен тұрады: А "28 саны жұп ", "28 саны 7 - ге бөлінеді ". Олар "және" деген логикалық жалғаулықтың көмегімен бір құрама сөйлемге келтірілген. Жәй сөйлемдердің белгіленуін пайдаланып, осы құрама сөйлемнің логикалық құрылымы "А және В" екенін айтуға болады. 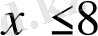"" сөйлемнің құрылу ерекшелігі бөлек. Егер А "х саны 8 - ге тең", "х=8" болса, В: "х саны 8 - ден кіші", яғни 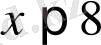"" онда оның логикалық құрылымы "А немесе В" болады.
Үшінші сөйлемде А: "үшбұрыш теңбүйірлі", В: "табанындағы бұрыштары тең" болса, онда оны "Егер А, болса онда В" түрінде жазуға болады.
"14 саны 4 - ке бөлінбейді" деген сөйлемнің логикалық құрылымын анықтау үшін А: "14 саны 4 - ке бөлінеді" деп алайық. Сонда берілген сөйлем "А емес", "А дұрыс емес" түрінде болады.
Бірқатар жәй хабарлы сөйлемдерді қарастырайық:
1. Қазақстан - егеменді мемлекет;
2. Натурал сандар жиыны ақырсыз;
3. 25 саны 5 - ке еселі;
4. Құр жиынның элементі бар;
5. 38 саны 3 - ке бөлінеді;
Бұл сөйлемдердің барлығы мазмұны жағынан әртүрлі. Бірақ олардың барлығына ортақ бір қасиеттің бар екенін байқауға болады. Осы ортақ - кейбір сөйлемдерде ақиқат (дұрыс, дәл), ал басқаларында жалған (дұрыс емес, қате) ойлардың айтылуы, 1, 2, 3, сөйлемдері ақиқат, ал 4, 5 сөйлемдер жалған деп есептейміз.
Хабарлы сөйлемнің ақиқат немесе жалған екендігін айтуға болса, онда ол пікір деп аталады.
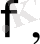
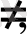
Математикада пікірлермен үнемі кездесіп отырамыз және ондай пікірлерді жазу үшін тағы басқа символдарды пайдаланамыз. Мысалы, 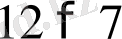"" пікір "12 саны 7 - артық" деген сөйлемнің математикалық жазылуы болып табылады. Кез келген хабарлы сөйлем пікір блмайтынын көрсетейік. Мысалы, 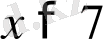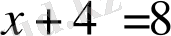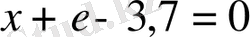"", "", "" сөйлемдері пікір бола алмайды, өйткені сөйлемдердегі айнымалылардың мәндері белгісіз болғандықтан олардың әрқайсысының ақиқат немесе жалған екендігі туралы айта алмаймыз. Қандай да бір сөйлем туралы ол ақиқат немесе жалған деп үнемі айта алмаймыз. Пікірлерді латын алфавитінің үлкне әріптерімен, ал лоардың мағынасы ақиқат болса, "а" әрпімен, жалған болса "ж" әрпімен белгілеу келісілген.
Ескерту: Кейбір оқулықтарда ақиқат және жалған деген сөздерді сәйкесінше 1 және 0 цифрларымен белгілейді.
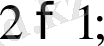
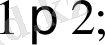
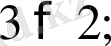
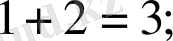
Бастауыш мектеп оқушылары математика пәнінің алғашқы сабағынан бастап ақиқат пікірмен кездеседі. Олар 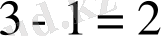тағы сол сияқты пікірлермен танысады. Одан кейін екі таңбалы, үш таңбалы сандар туралы пікірлер, күрделі сандық өрнектердің теңдігі, теңсіздігі туралы пікірлерге кездесетін болады. Мысалы, мына амалдардың дұрыс орындалғандығын не дұрыс орындалмағандығын тексеріңіздер:
517+408=925
804-235=579
Басқаша айтқанда, бұл жаттығуда берілген теңдіктердің ақиқат немесе жалған екендіктерін анықтау талап етіледі. Есептеу арқылы оқушы бірінші теңдіктің ақиқат, ал екінші теңдіктің жалған екендігіне көз жеткізеді.
Басқа жаттығуларда:
1.
2.
3.
4.
5. тағы сол сияқты жазылулардың дұрыс немесе
дұрыс емес екендігін анықтау талап етіледі.
Мұндай жаттығуларды орындауда пікір ұғымын пайдаланып отырмыз, өйткені берілген сөйлемдердің ақиқат немесе жалған екендігін анықтау талап етіліп отыр.
Пікірлер элементар (жәй) және күрделі (құрама) болып келеді. Элементар пікір деп оны басқа пікірлерге жіктеуге келмейтін пікірді айтамыз.
Егер пікірді бірнеше элементар пікірге жіктеуге болса, оны күрделі пікір деп атайды.
Күрделі пікір әртүрлі жалғаулықтар және сөз тіркестері арқылы элементар пікірлердер құрылады. Мысалы, "102 саны жұп және 9 - ға бөлінеді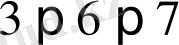", "" , "берілген төртбұрыш - ромб немесе квадрат" деген пікірлердің әрқайсысы күрделі. Олар элементар пікірлерді "және", "немесе" деген сөздермен байланыстыру арқылы алынып тұр.
Күрделі пікірлерді "егер", "онда", "сонда тек сонда ғана" деген сөздерді пайдаланып та алуға болады. Мысалы, "Егер үшбұрыштың екі қабырғасы тең болса, онда ол теңбүйірлі", "трапеция теңбүйірлі болса, сонда тек сонда ғана оны сырттай шеңбер сызуға болады".
Грамматикада "және", "немесе", "егер", "онда", "сонда тек сонда ғана" сөздерін жалғаулық деп атайды. Логикада оларды элементар пікірлер арасындағы байламдар деп атайды, өйткені мұндай жалғаулықтар элементар пікірлерді бір күрделі пікірге біріктіреді.
Сөйлем құрылысында қолданылатын "емес" сөзі мен, "дұрыс емес" деген тіркесті қарастырайық. Аталған тіркес қандай да бір пікірді теріске шығару мақсатында қолданылады: Мысалы, "12 жәй сан". Бұл - жалған пікір, себебі 12 саны 1 мен өзінен басқа да сандарға бөлінеді. Осы сөйлемге "емес", "дұрыс емес" сөздерін қолданайық. Одан қосақтасақ "12 жәй сан емес", "12 жәй сан деген дұрыс емес" деген сөйлемдер құрастырамыз. Ал, бұл - пікірлер ақиқат болады.
Сонымен, "және", "немесе", "егер", "онда", "сонда тек сонда ғана", "емес", "дұрыс емес" тағы басқа байламдар арқылы кез - келген элементар пікірлерден әртүрлі күрделі пікірлер алуға болады және олардың мағыналық сипатына көңіл аударылмайды. Пікірлер теориясында күрделі пікірге кіретін элементар пікірлердің ақиқат немесе жалған екендігіне байланысты күрделі пікірдің де ақиқат немесе жалған екендігі зерттеледі.
Кез келген А пікірінен, оны теріске шығара отырып, яғни А пікірі орындалмайды деп қабылдап, жаңа пікір алуға болады.
А пікірін теріске шығаруды 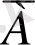деп белгілейді, ол "А емес" деп оқылады, мысалы, егер А - "Тік төрбұрышын диагональдары тең" деген пікір болса, онда 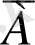- "Тік төртбұрышын диагональдары тең емес" деген пікір болады. Бұл мысалда А пікір ақиқат, ал 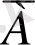пікір жалған.
Егер А - "128 саны жәй сан" десек, 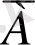- "128 саны жәй сан емес" деген пікірді білдіреді. Бұнда керісінше, А - пікірі жалған, ал 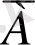- ақиқат пікір. Сонымен, А қандай пікір болғанымен, А және 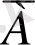екі пікірінің бірі - ақиқат, екіншісі - жалған болады. А және 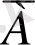арасындағы байланысты кесте арқылы көрсетуге болады. Мұндағы "а" әрпі ақиқат, "ж" әрпі жалған дегенді белгілейді. Осы түрдегі кестені ақиқаттық кесте деп атайды.

а
ж
ж
а

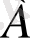
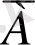
А қандай да бір пікір болсын. Сонда оның теріс пікірі 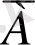-да пікір болып
табылады, ендеше 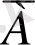пікірінің де, теріс 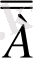пікірін қарастыруға болады. Оны А пікірін екі рет теріске шығару деп атайды. А пікірін екі рет теріске шығару, А пікірінің өзі екенін көрсету қиын емес. Оған 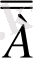пікірінің ақиқаттық кестесін құру арқылы көз жеткізуге болады. Басқаша айтқанда, кез келген пікірді екі рет теріске шығара отырып алғашқы пікірді аламыз, яғни .

а
ж
а
ж
а
ж

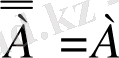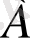
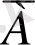
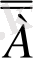
Егер айтылған пікірдегі баяндауышқа "емес" шылауын қоссақ, пікірдің теріске шығатынын көрдік. Ал егер А пікірдегі баяндауыштың "емес" шылауы болса, онда 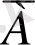пікірін құру үшін ол шылауды алып тастау керек.
Егер А - "бүгін күн суық емес" болса, 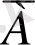- "бүгін күн суық" болады.
Мысалы:
А: "Асан - оқу озаты";
В: "Асан тәртіпті";
С: "Асан спортпен шұғылданады";
Д: "Асан саяхат құруды жақсы көреді" деген пікірлер берілсін.
Осы элементар пікірлерден мынандай күрделі пікірлер құруға болады:
1) "Асан оқу озаты және саяхат құруды жақсы көреді";
2) "Асан оқу озаты, тәртіпті және саяхат құруы жақсы көреді";
3) "Асан саяхат құруды жақсы көреді, ал спротпен шұғылданбайды";
4) "Асан спортпен шұғылданбайды және саяхат құруды жақсы көрмейтіні дұрыс емес";
Сонымен, нақтылы күрделі пікірдегі элементар пікірлерді әріптермен алмастырып берілген күрделі пікірдің логикалық құрылымын анықтайтын өрнекті аламыз. Осындай өрнек бар болса, онда оның ақиқат немесе жалған екендігін, яғни осы өрнекке сәйке келетін күрделі пікірдің ақиқат немесе жалған екендігін анықтауға болады.

Тұжырымдар логикасы. Тұжырым алғашқы ұғымдардың бірі, ол анықталмайды. Түсіндіріледі. Ақиқат немесе жалғандығы туралы айтуға болатын хабарлы сөйлем тұжырым болып табылады.
Мысалдар. Жер - күн жүйесінің планетасы (ақиқат тұжырым), Ай - жердің жасанды спутнигі (жалған), 43 (ақиқат), 25 (жалған), Әрбір нақты 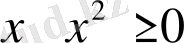(ақиқат), 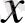нақты саны табылып 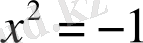орындалады (жалған) және т.б.
Бірақ әрбір хабарлы сөйлем тұжырым болып табылмайды. Мысалы, Бүгін ауа-райы тамаша сөйлемі ауа-райы жақсы ұғымының субъектілігіне байланысты тұжырым болып табылмайды. Әрбір сұраулы және әрбір лепті сөйлемдер тұжырым болып табылмайды. Анықтама да тұжырым емес.
Жеке тұжырымдарды 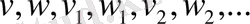әріптерімен белгілейміз. Сонымен, әрбір жеке тұжырым ақиқат немесе жалған, бірақ бір мезгілде екеуі де бола алмайды.
Мынадай келісімге келейік: егер 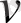тұжырымы ақиқат болса ол ақиқат мәнін қабылдайды және 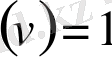. Егер 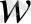тұжырымы жалған болса, онда ол жалған мәнін қабылдайды да .
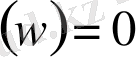Жай тұжырымдардан логикалық жалғаулардың көмегімен күрделі тұжырым жасауға болады. Ондай логикалық жалғаулар: ЖӘНЕ, НЕМЕСЕ, ЕМЕС, ЕГЕР...ОНДА... және т.б.

1.2 Оқушылардың математикалық сауаттылығы мен мынадай негізгі тақырыптары қамтылған:
Практикалық мазмұнды мәтінді есептер;
Бірнеше көп нұсқаның ішінен тиімді нұсқаны анықтау;
Функционалдық сауаттылықты анықтауға берілген ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.