Жүктелген денелерде атомаралық байланыстың қирауы

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 63 бет
Таңдаулыға:

Қазақстан Республикасы Білім және ғылым министрлігі

Қожа Ахмет Ясауи атындағы Халықаралық қазақ-түрік университеті

Физика кафедрасы

Арынова Ақбота

Қатты денелердің қирау концепция теңдеуіндегі 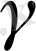коэффициентіне кристалл құрылымының әсері

ДИПЛОМДЫҚ ЖҰМЫС

5B060400 - «физика» мамандығы

Түркістан 2014

Қазақстан Республикасы Білім және ғылым министрлігі

Қ. А. Ясауи атындағы Халықаралық қазақ-түрік университеті

Физика кафедрасы

Қызметте қолдану үшін (қажет кезінде)

«Қорғауға жіберілді»

Кафедра меңгерушісі

ф-м. ғ. д., профессор Тұрмамбеков Т. А

ДИПЛОМДЫҚ ЖҰМЫС

Тақырыбы: Қатты денелердің қирау концепция теңдеуіндегі 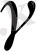коэффициентіне кристалл құрылымының әсері

5B060400 - «физика» мамандығы

Орындаған Арынова А.

Ғылыми жетекшісі

ф-м. ғ. д., профессор Бақтыбаев А. Н.

Түркістан 2014

МАЗМҰНЫ

Кіріспе . . . 4-7

1 Жүктелген қатты денелерде өтетін процестер . . . 8-11

1. 1 Қатты денелерді қирататын элементар акт процестері . . . 8-11

1. 2 Механикалық қирауда жүктелген жүктің рөлі және коэффициентінің

физикалық мәні . . . 12-16

1. 3 Жүктелген денелерде атомаралық байланыстың қирауы. Қираудың жинақталу кинетикасы . . . 16-19

2 Дененің құрылымын зерттейтін тәсілдер . . . 20-24

2. 1 Монокристалл мен поликристалдардың жарамдылық мерзімінің кернеу мен температураға тәуелділігі және блок бұрышы . . . 24-38

2. 2 Екіфазалы қорытпалардың және сәулелендірілген металдардың кейбір құрылымдық ерекшеліктері . . . 39-44

2. 3 Жарамдылық мерзім формуласындағы коэффициенттерге және жарамдылық мерзімге құрылым тұрақсыздығының әсері . . . 44-62

Қорытынды . . . ……. . 63

Пайдаланылған әдебиеттер. . …. . 64-65

Кіріспе

Заманауи ғылым мен техниканың дамуы барлық ғылым саласын қамтиды, соның нәтижесінде жаңа зерттеу бағыттары пайда болды. Сондықтан ол қалыптасқан теориялар мен көзқарастарды қайта қарауды талап етеді. Бұл күрделі зерттеу үдерістері және қайта қалыптастыру мақсатындағы зерттеулер беріктілік физикасында да орын алады. Кез келген материалдың беріктілігі сол материал қирамай өзінің біртұтастығын сақтайтын шама екендігі белгілі. Материалдардың қирауы қатты денелер физикасындағы ең актуалды проблемалардың бірі болып есептеледі. Материалдардың қирауын зерттеу - ғылым саласының ерекшелігі, ол қазіргі техникада экстремальді жағдайда жұмыс істей алатын жаңа материалдарды табу қажеттілігінен туындайды. Материалдың төзімділігін, жарамдылық мерзімін ұлғайту жолдарын қарастыру, сонымен қатар сол материалдың жұмыс атқару мерзімін алдын-ала болжау тәсілдерін дамыту ерекше орын алады. Жоғарыда айтылған проблемаларды шешуде материал қирауының физикалық табиғатын білу маңызды екендігі белгілі. Сонымен бірге бұл бағытта, материалдың деформациялану үдерісінің физикалық табиғатын зерттеу қирау секілді актуалды мәселе болып табылады.

Көп уақытқа дейін қатты денелердің қирау проблемасы таза механикалық көзқараста қарастырылып келген. Яғни қатты дененің қирауы тұтас денелер механикасы төңірегінде өз дамуын тапқан, ол берілген қасиетке байланысты серпімді түрде өтетін мәселелерді есептеу жолымен қарастырылады. Кейінгі кездерде серпімді түрде қарастырылып, соның нәтижесінде ол денеде кездесетін сызаттардың пайда болуынан денелердің қирауы төмендейтіндігі қарастырылады. Қирау физикасының дамуына атомаралық байланыс күштеріне негізделген теориялардың елеулі үлесі бар. Бұл теориялар арқылы бірнеше қатты денелердің теориялық беріктілігі анықталған, яғни материалдың теориялық беріктілігі нақты беріктіліктен 100-1000 есе төмен екендігі анықталған. Бұл қайшылықтарды түсіндіру мақсатында табиғаттағы кез келген қатты денелерде және олардың құрылымдарында ақаулар бар деп есептеледі. Атап айтқанда, материал ішіндегі микросызаттың болуынан деп есептеледі.

Бірақ дененің қирауын таза механикалық көзқараспен қарағанда, дененің қирауы критикалық құбылыс деп қарастырылады. Яғни дененің механикалық тепе-теңдігі, оқшауланған серпімді механикалық кернеу (σ _оқ ) критикалық шамасына жеткенде, дене теңсіздігін жоғалтып қирайды. Дененің қирауына физикалық көзқараспен қарап, ол көзқарастың ары қарай дамуын ΧΧ-шы ғасырдың 50-ші жылдары академик С. Н. Журков қарастырған. Нәтижесінде ол қатты дене қирауының кинетикалық концепциясын ұсынған [1] .

Бұл концепция өзінің дамуын В. Р. Гегель, В. А. Степанов және басқа да зерттеушілердің еңбектерінде жалғасын тапты [2] .

Қираудың кинетикалық концепциясы бойынша болған кезде, қирау үдерісі термофлуктуациялық әсерден басталатындығы дәлелденген. Денені жүктеген кездегі механикалық кернеу атомаралық байланыстағы потенциалдық тосқауылды төмендетеді. Бұл тосқауыл қирауға қажетті энергия шамасына тең болады. Сол себепті механикалық кернеу дененің қирауына бағыт береді. Денелердің қирау механизмін термофлуктуациялық үдеріс деп есептеп, бұл зерттеу жұмысында кристалдық құрылымға ие қатты денелердің кинетикалық қирау заңдылықтары, атап айтқанда иондық кристалдар қарастырылған. Сондықтан зерттеуге қойылған нақты шешілетін мәселелерді қарастырайық. Бірақ нақты мәселелерді қарастырудан бұрын қарастырылып шешілген мәселелерге тоқталайық.

[2] еңбекте дененің қирауын кинетика-термофлуктуациялық үдеріс деп атауға түрткі болған негізгі мәліметтерді қарастырайық.

1920-шы жылдары дене пластиктивтілігінің температураға және жүктеу жылдамдығына тәуелділігі зерттелініп, Беккерь мынадай ой-пікірді ұсынған: дененің пластиктивтілігін зерттегенде, дене атомдарының жылулық қозғалысын ескеру қажет. Беккерьдің ой-пікірі бойынша термофлуктуация үдерісі, жүктелген денедегі жақыннан әсерлесудің тосқауылдан өтуіне көмектесіп, пластикалық ығысуға алып келеді. Яғни пластикалық деформацияны термоактивациялық үдеріс деп қарастыруды ұсынған.

Термофлуктуациялық үдерістің негізгі рөл атқаратынын және атом-молекулалық бөлшектердің механикалық күш өрісінде қайтадан орналасып, нәтижеде деформациялық және релакцияциондық үдерістің дамуына алып келу мәселелері [3] еңбектерде талданған.

Жүктелген денеде дене формасының өзгеруін талдай отырып, механикалық күш өрісіндегі атомдар жүйесі потенциал тосқауылдарынан өтуін термофлуктуация деп атайды.

Сонымен пластикалық деформация мен релаксация үдерістерін термофлуктуациялық үдеріс деп есептеу ертеден-ақ басталған. Бұл көзқарас бірнеше еңбектерде дислокациялық теория негізінде қарастырылып, мысалы [4-5] еңбекте алынған нәтижелер қираудың кинетикалық концепциясын ұсынуға өзінің үлесін қосқан.

Шынында да, бір-бірімен байланысты қирау және деформация құбылыстарының табиғатта елеулі айырмашылықтары бар: деформация термофлуктуациялық және кинетикалық үдеріс болса, ал қирау атермикалық және критикалық үдеріс болып табылады. Дегенмен, қираудың кинетикалық концепциясы негізінде экспериментальды түрде алынған нәтижелер жатады. Ол нәтижелерге қарағанда қатты денелер беріктілігінің температураға, уақытқа тәуелділігі: беріктілік шегінің кернеуге және температураға тәуелділігі; жоғары температуралы жылжығыштық және жоғары мерзімді беріктілік. Ал ең негізгісі беріктілікке әсер еткен күштің мерзімі болып есептеледі. Бұл мәліметтерді статикалық шаршау деп атайды және ол мәліметтер кейбір металдарға, ас тұзына, болаттарға, бір топ қатты денелерге екені анықталған. Бірақ барлық анықталған мәліметтердегі беріктілікке уақыттың тәуелділігін қосымша фактор деп есептейді, яғни қирау критикалық түрде өтеді.

Қатты дене қирауының негізінде жататын беріктіліктің уақытқа тәуелділігін дәлелдеу мақсатында жүйелі зерттеу нәтижелеріне қарағанда беріктіліктің уақытқа тәуелділігі ортаның құрылымының гетерогендігінде, яғни құрылымның біртексіздігінде емес, ол факторлар беріктіліктің уақытқа тәуелділік заңдылығына қосымша фактор болып есептеледі.

Беріктілікке температураның әсерін жүйелі түрде зерттеу Ресей ғылым академиясының А. Ф. Иоффе атындағы физика техникалық институтта басталған. Сол институтта жүргізілген Журковтың, Регельдің, Нарзуллаевтың, Санфированың, Томашевскийдің бірінші жүргізілген тәжірибелеріне қарағанда беріктіліктің уақытқа тәуелділігі әртүрлі қатты денелерде орын алады. Ол зерттелген қатты денелердің поликристалды құрылымға ие алюминий, никель, мырыш, платина металдары және алюминий негізіндегі екі түрлі қатты ерітінділер жатады [6] .

Жарамдылық мерзімінің τ сыртқы бір бағытта тартатын механикалық кернеуге σ және сынау температурасына тәуелділігі [7] еңбекте көрсетілген. Ол еңбектегі параметрлер арасындағы талдай отырып, барлық зерттелген қатты денелерге мынадай түрдегі параметрлер қатынасына бағынатындығы анықталған:

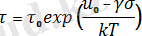
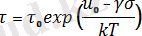(1)

Мұндағы, - белгілі σ кернеуіндегі және t температурадағы сол материалдың жарамдылық мерзімі.

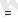
τ ₀ - t 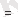10 ^-12 - 10 ^-13 с температураға тәуелсіз жарамдылық мерзім.

u ₀ - зерттелген қатты дененің жүктелмеген кездегі қирау активация энергиясы.

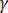
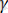- активациялық көлем.

Температура тұрақты болғанда 1- ші теңдеу мына түрде болады:

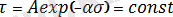
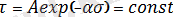(2)

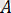
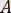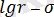
мұндағы, және коэффициенттері 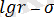координатадағы тура сызықтың иілгіштігімен анықталады.

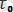
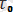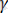
, u _0, 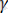тұрақты коэффициенттер және коэффициенттерімен төмендегі формула арқылы байланысқан:

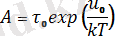
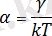
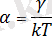; (3)

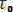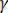
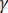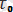
, u _0, параметрлерді талдаған нәтижелеріне қарағанда, 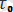барлық зерттелген қатты денелерде бірдей екендігі, яғни дәрежесі 10 ^-12 -10 ^-13 аралғында жататындығы және ол жарамдылық мерзім атомның жылулық тербеліс периодына тең екендігі анықталған.

Біз қарастыратын зерттеулерде құрылымның жарамдылық мерзімге әсерін анықтауға болады. Бірінші теңдеу арқылы u ₀ шамасын анықтау, жоғарыда көрсетілген шарттар арқылы анықтауды мынандай деп тұжырымдауға болады. Алдын-ала анықталған [7] мәліметтерде бірінші формуладағы γ- коэффициенттің шамасын құрылым сезімтал коэффициенті деп қабылдап, белгілі күйдегі бір топ үлгілерге, атап айтқанда алдын-ала күйдіру, прокаттау дәрежесі тағы басқа өңделген үлгілердің γ- коэффициенттің мәндері бірдей деп қабылданады және әртүрлі температурада және кернеуде жылжығыштық режимде сынаған кездегі қираған үлгілері өзгермейді.

Қорытындылай келе, кристалдардың қирау кинетикасын анықтау мақсатында феноменологиялық микроқұрылымдық зерттеу нәтижелері бір - біріне қарама - қарсы көзқарастарды тудырады.

Дипломдық жұмыстың өзектілігі: Заманауи ғылым мен техниканың дамуы барлық ғылым саласын қамтиды, соның нәтижесінде жаңа зерттеу бағыттары пайда болды. Сондықтан ол қалыптасқан теориялар мен көзқарастарды қайта қарауды талап етеді. Бұл күрделі зерттеу үдерістері және қайта қалыптастыру мақсатындағы зерттеулер беріктілік физикасында да орын алады. Кез келген материалдың беріктілігі сол материал қирамай өзінің біртұтастығын сақтайтын шама екендігі белгілі. Материалдардың қирауы қатты денелер физикасындағы ең актуалды проблемалардың бірі болып есептеледі. Материалдардың қирауын зерттеу - ғылым саласының ерекшелігі, ол қазіргі техникада экстремальді жағдайда жұмыс істей алатын жаңа материалдарды табу қажеттілігінен туындайды. Материалдың төзімділігін, жарамдылық мерзімін ұлғайту жолдарын қарастыру, сонымен қатар сол материалдың жұмыс атқару мерзімін алдын-ала болжау тәсілдерін дамыту ерекше орын алады. Жоғарыда айтылған проблемаларды шешуде материал қирауының физикалық табиғатын білу маңызды екендігі белгілі. Сонымен бірге бұл бағытта, материалдың деформациялану үдерісінің физикалық табиғатын зерттеу қирау секілді актуалды мәселе болып табылады.

Дипломдық жұмыстың мақсаты: Жарамдылық мерзімге механикалық кернеу мен температураның әсерін анықтау - дене қирау заңдылығының феноменологиялық талдауының негізі болып табылады. Бірақ бұл талдаудың дұрыс екендігін анықтау мақсатында зерттелген дененің құрылым элементін тексеріп отыруды қажет етеді. Себебі, дене құрылым элементі ол дененің жарамдылық мерзіміне өзінің әсерін тигізеді. Сондықтан кез келген қатты дененің құрылым элементін анықтау және оның жарамдылық мерзіммен байланыстығын анықтау - дипломдық жұмыстың негізгі мақсаты болып есептеледі.

Жұмыстың құрылымы: Дипломдық жұмыс кіріспе, екі тарау, қорытынды және пайдаланылған әдебиеттер тізімінен тұрады.

1 Жүктелген қатты денелерде өтетін процестер

1. 1 Қатты денелерді қирататын элементар акт процестері

Қатты денелердің қирау табиғаты термофлуктуациялық екендігін біз жоғарыда айтып өттік. Бірақ бұл процестің сондай екендігін белгілі қатты дене үшін дәл анықтаған (қарастырған) жоқпыз. Атом - молекулалық деңгейде, яғни микропроцестер жөнінде мәліметті тек макрохарактеристиканы анықтау арқылы, атап айтсақ жүктелген дененің жарамдылық мерзімін анықтау арқылы алдық.

Енді, алдымен, металдарда элементар қирау процесінде кездесетін акттарды қарастырайық. Бізге белгілі, металдардың әрбір атомы симметрия түрде басқа атомдармен қоршалған (ақауларды есепке алмағанда) және өзара әсерлеседі.

Әрбір атомның байланыс энергиясы атомаралық байланыс энергиясының жақын орналасқан атомдар санының көбейтіндісіне тең. Активациялық түрде металдың кристалдық торында әр түрлі процестер кездесуі мүмкін. Бұл процестерді әр түрлі ақаулардың пайда болуына (нүктелі, сызықты және беттік ақаулар) және ол ақаулардың орын ауыстыруына байланысты деп айтуға болады. Бұл процестер белгілі активациялық энергиямен жүріп отырады. Металдардың жарамдылық мерзімін анықтау теңдеуіне қарағанда бастапқы қирау активациялық энергия шамасы 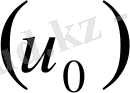атомдардың булану немесе сублимация энергия шамасына тең. Металл бетінен атомдардың булану барысында, әрбір атомның метал бетінен шығу актінде кристал торынан координация санының жартысына тең атом байланыстары қирайды.

Сонымен әрбір атомның булану энергиясы сол атомның толық байланыс энергиясының жартысына тең екендігін есептеу қиын емес, ол үшін әрбір атомаралық байланыс екі атомдікі екенін ескеріп, металдың барлық атомаралық байланыстарын анықтау арқылы табуға болады. Бірақ металдың қирау процесі атомдардың булану процесі деп айтуға болмайды. Кейбір жағдайда осындай процесс деп айту да мүмкін. Мысалы, сызат ұшынан атомдардың ұшуы, соның арқасында сызаттың өсуі, сонымен металдың қирауы. Бірақ басқа да процестер болуы мүмкін, ол процестердің энергиясы сублимация энергиясына тең болуы мүмкін. Сол процестердің бірін қарастырайық.

Металдың екіге бөлінуін екі атом қабыршағында атом байланысының қирауы арқасында деп түсінсек, бұл қирау энергиясын әрбір атом байланысына шаққанда (бөлгенде), оның шамасы сублимация энергия шамасынан елеулі кем. Себебі, әрбір атомның қираған байланыс саны түйіндегі байланыс санының жартысынан кем. Сол себепті, дененің екіге бөлінуін сызаттардың үлгі көлденең кесімінен таралып өсуімен түсіндіру оңай. Олай болса, дененің қирау жылдамдығы сызат фронтының қозғалу жылдамдығына тең. Сызаттың бұл қозғалуын механикалық деңгейде бірденінен сызықты, фронттың белгілі жылдамдықпен қозғалуы деп қарастыруға болады. Ал флуктуациялық қирау құбылысы тізбектеліп, бірінің артынан бірі атомаралық байланыстың үзілуімен өтеді. Яғни сызат фронтының бір бөлігінде жылжып (қажетті флуктуация жеткен бөлігінде), қалған сызат бөлегі жылжып оларға қосылады, сонымен сызат фронты тағы да тура сызықты болады. Қазіргі кезде флуктуациялық қозғалыс кристалдағы сызықты ақаулардың (дислокация) торда қозғалуымен түсіндіріледі. Дислокация, алдымен екі рет баспалдақ (перегиб) жасап, ол ары қарай екі жаңа дислокация бойымен кеңейеді. Бұл процесті схема түрінде былай көрсетуге болады:

F - әсер етуші күш бағыты. Тік (вертикаль) сызықтар - дислокация

сызығы.

Баспалдақ пайда болу үшін қажет активациялық энергия, «б» баспалдақтың кеңеюіне қажет болған активация энергиясынан әлдеқайда жоғары. Сол себепті, дислокацияның жылжу жылдамдығын, баспалдақ пайда болу актын күтуімен анықталады. Осы сияқты, сызат фронтының орын ауыстыруын (қозғалуын) сипаттауға болады.

Ескерте кету қажет , бұл дислокацияның қозғалу және сызаттың орын ауыстыру модельдері әр уақытта орын алады деп айтуға болмайды. Себебі, басқа процестердің активациялық энергия шамасы, мысалы, өздік диффузия, ендірілген атомдардың пайда болуы (ішкі сублимация), баспалдағы бар дислокациялардың қозғалуы, дислокациялардың қиылысуы, екі ретті дислокацияның баспалдағы, дислокацияның тосқауылдан босалып шығуы т. б. сублимация энергияға жақын. Сол себепті, қирау энергия шамасын талдау ғана үлкен мәнге ие болмай, бұл шамаға металдың күйі қандай әсерін тигізетінін анықтаудың үлкен мәні бар. Мысалы, күйдіру, әр түрлі механикалық өңдеу, легирлеу т. б.

Металдардың қирауын зерттегенде, қирау активациялық энергия шамасы металдардың күйін кеңінен өзгертуден, мысалы, қоспа атомдардың концентрациясын, дислокацияның тығыздығын т. б. метал құрылымын өзгертуден өзгермейтіндігі анықталған. Сонымен бірге бұл өзгерістерге, металдағы басқа процестердің сезгіштігі байқалған. Мысалы, таза күміске қоспа атомдарының қосылуы өздік диффузия энергиясының өзгеретіндігі, ал сублимация энергиясына және қирау активация энергиясына әсерін тигізбейтіндігі анықталған. Сонымен бірге қоспа атомдар, диффузия процесінің активация энергиясына және дислокация процестеріне әсерін тигізетіндігі анықталған. Сол себепті, қирау элементар акты, сублимация актына жақын деп есептеуге болады. Бірақ, металдарда қирау элементар процесінің мәселесі толық шешілген деп айтуға болмайды. Атомаралық байланыстың қирауын термофлуктуациялық модельмен түсіндіру, жалпы қирау мәселесінің негізін бергенмен және металдардың механикалық қирауын түсіндіруде бастамасы болғанмен, толық шешімін бере алмайды. Металдардың қирауын толық шешу үшін, атом-молекулалық деңгейде тәжірибе қою арқылы, бұл термофлуктуациялық гипотезаны дәлелдеу қажет.

Енді полимер материалдарының қирау элементар актын қарастырамыз. Полимер материалдарының металдардан айырмашылығы, полимерлердің атомаралық байланысын екіге бөлуге болады: полимер тізбектеріндегі күшті байланыс (химиялық) және тізбектер аралығындағы не болмаса бір тізбектің бөлшектер аралығындағы әлсіз (Ван-дер-Вальстық, сутектік) байланыстар. Сол себепті, бұл материалдың қирауын қандай байланыстардың үзілгендігі анықтайды: молекула ішіндегі байланыстың үзілуі ма (химиялық байланыс) не болмаса молекулааралық (Ван-дер-Вальстық) байланыстың үзілуі ма деген сұрақ туады.

Полимерлердің қирау активациялық энергиясының 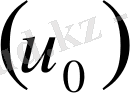химиялық байланыстарының үзілуі, активациялық энергиясына тең екендігі белгілі. Бірақ, бұл екі энергияның теңдігі полимердің атомдық қирау механизмін анықтамайды. Себебі, бұл қирау активациялық энергиясы, әлсіз молекулааралық байланыстардың үзілу активациялық энергиясының жинақталуымен шыққан шамада болуы мүмкін.

Бірақ полимердің қирау активациялық энергиясының химиялық байланыстың үзілу активациялық энергиясына теңдігі, қосымша жүргізілген тәжірбиелер сапалы түрде дәлелдейді. Мысалы, полимер күйін, оларды пластификациялау, молекула тізбегін ориентациялау және сәулелендіру арқылы өзгерту, полимерлердің бастапқы қирау активациялық энергия шамасын 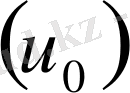өзгертпейді. Бұл жағдай полимерлерді қирауға алып келетін элементар акт, макромолекуладағы керілген химиялық байланыстың термофлуктуациялық қирауы деп есептеуге болады. Бірақ полимердің жарамдылық мерзімін анықтау арқылы, 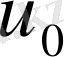- дің физикалық мәні толық шешілді деп айтуға болмайды. Себебі керілген макромолекуланың үзілуі, термофлуктуациялық процесс деп айтудың қиыншылықтары бар. Оған қосымша, полимерлер белгілі күйде молекулааралық байланыстың үзілуінен қирайды. Мысалы, әрбір полимердің белгілі температурадан жоғары болған кездегі қирауы.

Тағы да бір ескеретін жағдай, қатты денелердің қирауы, керілген атомаралық байланыстың уақыт барысында термофлуктуациялық қирау акты өту нәтижесі деп есептеу, жеңілдетілген жағдай. Шынында да, дене жүктелгеннен бастап элементар қирау актынан басқа (атомаралық байланыстардың үзілуі), дененің деформациялануына алып келетін акттар (атомдардың және молекулалардың қайтадан топталу акты, металдарда нүктелі, сызықты және беттік ақаулардың орын ауыстыруы, полимерлерде ориентациялық процестердің жүруі т. б. ) бар. Сол себепті, қирауды нақты талдағанда, қирау процесін деформация процесімен байланыстырып есепке алу қажет. Сонымен бірге, әрбір элементар актының қирау процесіне қосатын үлесін анықтауды қажет етеді.

Дене қирауының дамуына, қираған байланыстардың жинақталуы қажет, яғни жүктелген денеде қираған байланыстардың рекомбинацияланбауы керек екендігі белгілі. Бұл шарт, қираған байланысты қоршайтын орта қасиетіне белгілі шарт тудырады. Шынында да, егер кристалдық тордағы екі атомаралықтағы байланыс, флуктуация әсерімен қирап, жүктелген жүк елеулі арақашықтыққа бірінен-бірін ажыратпаса, басқа бір көрші атомаралық байланыстың қасына орналасады. Сонымен ол үзілген байланыс қайтадан орнына келеді. Бұл байланыстың орнына келуі, тек көрші атомдар өздерінің орналасуын өзгертіп үлгермеген жағдайда болуы мүмкін. Қираған байланыстың сақталуы үшін (қираған күйінде қалу үшін), сол атомның қасында елеулі деформация жүруі керек. Сонда ғана байланыс қайтадан орнына келмейді. Сонымен, уақыт барысында қираған байланыстың қасында не болмаса кіші шамадағы арақашықтықта тағы бір флуктуациялық қирау процесі жүріп, ары қарай осылай жалғаса береді. Қирау процесі даму үшін, қираған байланыстың қасында өзгерістер болуы керек. Осы қарастырылған процестер полимерлерде орын алады. Шынында да, қираған макромолекула қайтадан орнына келмеу үшін, яғни рекомбинация процесін тоқтату үшін, қираған макромолекула ұштары бірінен-бірін алшақтауы керек.

Бұл қарастырылған мәселелер элементар қирау акты түсінігіне елеулі қиындықтар туғызады. Қирау процесінің активациялық энергиясын белгілі эффективті шама, ол күрделі байланысқан әр түрлі процестерді көрсетеді. Мысалы, элементар байланыс, қирау акты және атомдардың қайтадан топталуы.

Шынында да, дененің қирауына атом байланыстарының үзілуі жеткіліксіз, ол қираған байланысты бірінен-бірін ажыратып, қайтадан байланысты болмайтындай етіп қою керек. Олай болса, үзілген байланысты ажырату үшін де, уақыт керек және ол процесс өзінің белгілі активация энергиясына ие. Бұл жағдайда жарамдылық мерзім екі процестің өтуіне : қирау және қираған байланысты ажыратуға кетеді екен. Сонымен бұл екі процесс, есептелетін активация энергия шамасына 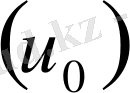өзінің үлесін қосады. Деформация процесі дененің қирау барысында тек рекомбинация процесіне жол қоймау ролін атқармай, бұл процесс байланыстың қирау акты алдында өтіп, атом байланыстарын жүктеуге (керуге) көмектеседі.