ҚАТТЫ ДЕНЕНІҢ ІШКІ ҚҰРЫЛЫМЫ

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 70 бет
Таңдаулыға:

МАЗМҰНЫ

КІРІСПЕ . . . 3

1 ҚАТТЫ ДЕНЕНІҢ ІШКІ ҚҰРЫЛЫМЫ. КРИСТАЛ ТОРЫ . . . 13

1. 1 Қатты денелердегі анизотропия. Моно және поликристалды қатты денелер. Химиялық элементтердің кристалдық құрылымдары . . . 17

1. 2 Кристалдардағы құрылым жетіспеушілігі. Түйін аралық атомдар және ваканция. Электрондар және кемтіктер. Дислокациялар және экситондар . . . 23

1. 3 Дислокация. Дислокация көздері. Дислокациялардың өзара әсерлесуі . . . 38

2 МЕТАЛДАР МЕН КРИСТАЛДАРДАҒЫ МИКРОСЫЗАТТАР . . . 49

2. 1 Микросызаттарды зерттейтін тәсілдер. Кіші бұрышты рентген сәулесінің шашырауы. Жарықтың шашырауы . . . 48

2. 2 Ақау тығыздығын өлшеу. Элекртондық микроскопия. Микросызат ұрығының өлшемі, концентрациясы және формасы . . . 51

2. 3 Электрондық микроскопия көмегімен микросызаттарды анықтау. Деформациядан тығыздықтың төмендеуі . . . 53

ҚОРЫТЫНДЫ . . . 69

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР . . . 70

Кіріспе

Қазіргі заманда ғылым мен техниканың дамуы барлық ғылым саласын қамтиды, нәтижеде жаңа зерттеу бағыттары пайда болады. Сонымен қатар қалыптасқан теорияларды және көзқарастарды қайтадан қарауды талап етеді. Бұл терең зерттеу үдерістері және қайтадан қалыптастыру мақсатындағы зерттеулер беріктілік физикасында да орын алады. Кез келген материалдың беріктілігі сол материал қирамай өзінің біртұтастығын сақтайтын шама екендігі белгілі.

Материалдардың қирау проблемасы қатты денелер физикасындағы ең актуалды проблемалардың бірі болып есептеледі. Материалдардың қирауын зерттеу ғылым саласының ерекшелігі қазіргі техникада экстремальді жағдайда жұмыс істей алатын жаңа материалдарды табу қажеттілігінен туындайды.

Материалдың төзімділігін, жарамдылық мерзімін ұлғайту жолдарын қарастыру, сонымен қатар ол материалдың жұмыс атқару мерзімін алдын-ала болжау тәсілдерін дамыту тағы басқа орын алады.

Жоғарыда айтылған проблемаларды шешуде материал қирауының физикалық табиғатын білумен тығыз байланыста екендігі белгілі. Сонымен бірге бұл бағытта материалдың деформациялану үдерісінің физикалық табиғатын зерттеу қираумен қатар актуалды мәселе болып табылады. Көп уақытқа дейін қатты денелердің қирау проблемасын таза механикалық көзқараста қарастырылған. Яғни қатты дененің қирауы тұтас денелер механикасы төңірегінде дамуын тапқан. Яғни берілген қасиетке байланысты серпімді өтетін мәселелерді есептеу жолымен қарастырылады. Кейінгі кездерде серпімді қарастырылған, соның арқасында ол денеде кездесетін сызаттардың болуынан денелердің қирауы төмендейтіндігі қарастырылады.

Қирау физикасының дамуына атомаралық байланыс күштерге негізделген теориялардың елеулі үлесі бар. Бұл теория арқылы бірнеше қатты денелердің теориялық беріктілігі анықталған. Бұл еңбектерге қарағанда материалдың теориялық беріктілігі 100-1000 есе нақты беріктіліктен төмен екендігі анықталған. Бұл қайшылықтарды түсіндіру мақсатында табиғаттағы кез келген қатты денелерде, олардың құрылымында ақаулар бар деп есептеледі. Атап айтқанда, материалдың ішінде микросызаттың болуынан деп есептеледі. Бірақ, дененің қирауын таза механикалық көзқараспен қарағанда дене қирауы критикалық құбылыс деп қарастырылады.

Дене қирауына физикалық көзқараспен қара, ол көзқарастың ары қарай дамуына ΧΧ-шы ғасырдың 50-ші жылдары академик С. Н. Журков қарастырған. Нәтижесінде қатты дене қирауының кинетикалық концепциясын ұсынған.

Бұл концепция өзінің дамуын В. Р. Регель, В. А. Степанов және басқа да зерттеушілердің еңбектерінде қарастырылған.

Қираудың кинетикалық концепциясы бойынша болған кезде қирау үдерісі термофлуктуациялық әсерден басталатынын дәлелдеген. Денені жүктеген механикалық кернеу атомаралық байланыстағы потенциалдық тосқауылды төмендетеді. Ол тосқауыл қирауға қажетті энергия шамасына тең болады. Сол себепті механикалық кернеу дененің қирауына бағыт береді.

Денелердің қирау механизмін термофлуктуациялық процесс деп есептеп, бұл зерттеу жұмысында кристалдық құрылымға ие қатты денелердің кинетикалық қирау заңдылықтары қарастырылған. Атап айтқанда, иондық кристалдар қарастырылған. Бірақ алдымен зерттеуге қойылған нақты шешілетін мәселелерге тоқтайық. Нақты мәселелерді қарастырудан бұрын қарастырылып шешілген мәселелерге тоқтайық. [1] еңбекте дененің қирауын кинетикалық термофлуктуациялық үдеріс деп атауға түрткі болған негізгі мәліметтерді қарастырайық.

1920-шы жылдары дене пластиктивтілігінің температураға, жүктеу жылдамдығына тәуелділігі зерттеліп Беккерь мынадай ой-пікірді ұсынған.

Дене пластиктивтілігін зерттегенде дене атомдарының жылулық қозғалысын ескеру қажет. Беккерьдің ой-пікірі бойынша термофлуктуация жүктелген денедегі жақыннан әсерлесу тосқауылдан өтуге көмектесіп, пластикалық ығысуға алып келеді. Яғни пластикалық деформацияны термоактивациялық үдеріс деп қарастыруды ұсынған.

Термофлуктуациялық үдерістің негізгі рөл атқаратынын және атом-молекулалық бөлшектердің механикалық күш өрісінде қайтадан орналасып, нәтижеде деформациялық және релакцияциондық үдерістің дамуына алып келу мәселелері[1-2] еңбектерде талданған.

Жүктелген денеде дене формасының өзгеруін талдай отырып, [1-2] еңбектердің авторлары механикалық күш өрісіндегі атомдар жүйесі потенциал тосқауылдарынан өтуін термофлуктуация деп есептеген.

Сонымен пластикалық деформация және релаксация үдерістері термофлуктуациялық үдеріс деп есептеу ертеде басталған. Бұл көзқарас бірнеше еңбектерде дислокациялық теория негізінде қарастырылып, мысалы [2-3] еңбекте алынған нәтижелер қираудың кинетикалық концепциясын ұсынуға өзінің үлесін қосқан.

Шынында да, бір-бірімен байланысты қирау және деформация елеулі айырмашылықтары бар: деформация термофлуктуациялық және кинетикалық болса, қирау атермикалық және критикалық түрде өтеді.

Дегенмен, қираудың кинетикалық концепциясы негізінде экспериментальды түрде алынған нәтижелер жатады. Ол нәтижелерге қарағанда қатты денелер беріктілігінің температураға, уақытқа тәуелділігі: беріктілік шегінің кернеуге және температураға тәуелділігі [18] ; жоғары температуралы жылжығыштық және жоғары мерзімді беріктілік мысалы, [19] . Ал ең негізгісі беріктілікке әсер еткен күштің мерзімі болып есептеледі.

Бұл мәліметтерді статикалық шаршау деп атайды және ол мәліметтер кейбір металдарға [21], ас тұзына [22], болаттарға [23], бір топ қатты денелерге [24, 25] екені анықталған. Бірақ барлық [5] -ке дейінгі анықталған мәліметтердегі беріктілікке уақыттың тәуелділігін қосымша фактор деп есептейді. Яғни қирау критикалық түрде өтеді деген ой-пікірде қалған [26] . Мысалы, [4] еңбекте беріктіліктің уақытқа тәуелділігін қатты дене құрылымы тұтқыр-серпімді гетерогендікпен түсіндірілді. Яғни, жүктің уақытқа тәуелділігі дененің ішінде кернеудің бөлінуімен байланыстырылды. Ол бөлінудің арқасында үлгінің серпімді бөлігінде кернеу пайда болып дененің лезде қирауына алып келеді. Ал [5] еңбекте беріктілік шегіне уақыттың әсерін материалдың құрылымы біртексіздігімен байланысты. Атап айтқанда, бұл ой-пікір күйдіріп-шыңдалған болаттың беріктілігіне қатысты. Белгілі уақыт аралығында құрылым өзгереді. Сондықтан шамасы төмендейді. Бұл ой-пікір [6] еңбектегі мәселелерді біршама нақтырақ қарастырады.

Қатты дене қирауының негізінде жататын беріктіліктің уақытқа тәуелділігін дәлелдеу мақсатында жүйелі зерттеу нәтижелеріне қарағанда беріктіліктің уақытқа тәуелділігі ортаның құрылымының гетерогендігінде. Яғни құрылымның біртексіздігінде емес, ол факторлар беріктіліктің уақытқа тәуелділік заңдылығына қосымша фактор болып есептеледі.

Беріктілікке температураның әсерін жүйелі түрде зерттеу Ресей ғылым академиясының А. Ф. Иоффе атындағы физика техникалық институтта басталған. Сол институтта жүргізілген Журковтың, Регельдің, Нарзуллаевтың, Санфированың, Томашерскийдің бірінші жүргізілген тәжірибелеріне қарағанда беріктіліктің уақытқа тәуелділігі әртүрлі қатты денелерде орын алады.

Ол зерттелген қатты денелердің поликристалды құрылымға ие алюминий, никель, мырыш, платина металдары жатады және алюминий негізіндегі екі түрлі қатты ерітінділер жатады.

Жарамдылық мерзімінің τ сыртқы бір бағытта тартатын механикалық кернеуге σ және сынау температурасына тәуелділігі [7] еңбекте көрсетілген. Ол еңбектегі параметрлер арасындағы талдай отырып, барлық зерттелген қатты денелерге мынадай түрдегі параметрлер қатынасына бағынатындығы анықталған:

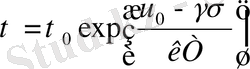(1)

Мұндағы, - белгілі σ кернеуіндегі және t температурадағы сол материалдың жарамдылық мерзімі.

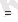
τ ₀ - t 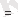10 ^-12 - 10 ^-13 с температураға тәуелсіз жарамдылықмерзім.

u ₀ - зерттелген қатты дененің жүктелмеген кездегі қирау активация энергиясы.

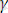
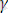- активациялық көлем.

Температура тұрақты болғанда 1- ші теңдеу мына формулаға [10] .

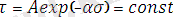
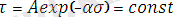(2)

Мұндағы, А және α коэффициенттері координатадағы тура сызықтың иілгіштігімен анықталады.

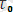
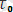, u _{0

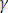
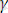,} тұрақты коэффициенттерА және α коэффициенттерімен төмендегі формула арқылы байланысқан.

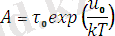
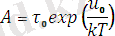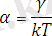
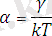; (3)

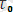
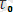, u _{0

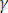
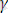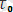
,} параметрлердің талдаған [5] еңбектің нәтижелеріне қарағанда exp алдындағы 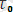барлық зерттелген қатты денелерде бірдей екендігі, яғни дәрежесі 10 ^-12 -10 ^-13 аралғында жататындығы және ол жарамдылық мерзім атомның жылулық тербеліс периодына тең екендігі анықталған, u ₀ - параметр материалдан материалға өткенде өзгеретіндігі, бірақ әрбір материалға оның ішкі құрылымына тәуелсізбірдей екендігі анықталған. Мысалы, жоғарыда көрсетілген металдар үшін u ₀ -дің мәні ол материалдың бастапқы механикалық және термикалық өңдеулеріне тәуелсіз екендігі анықталған. Әрбір зерттелген металдың u ₀ мәні сол металдар атомдарының жылулық ыдырау энергиясына тең екендігі анықталған. Яғни сол металдың сублимация энергиясына тең екендігі анықталған. 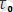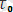және u ₀ - дің сәйкесінше атомдардың тербеліс периодына және байланыс энергиясына теңдігі денелерден кинетикалық, термофлуктуациялық процестермен байланыстыруға болатындығын көрсетеді. Соның негізінде [5] - ші еңбекте ұсынылған материалдың қирау процесіне, яғни уақыт барысында жүктелген атомаралық байланыстың ыдырауын біртіндеп және қайтымсыз өтетін процеспен байланысты деген ой-пікірге негіз бола алады. Бұл қайтымсыз процесс дененің бірнеше бөлікке бөлінген кезде тоқтайды. Бұл қайтымсыз ыдырау процесі жүруде негізгі рольді атомдардың жылулық қозғалысы атқарады, әсіресе жылулық флуктуация, яғни атомдардың орташа kT энергиясы аймағындағы флуктуация атқарады.

Жоғарыда айтылған ой-пікірлерге сүйене отырып, беріктіліктің уақытқа тәуелділігін анықтағанда ең негізгі мәселе-қатты денелердің қирау табиғатының кинетикасын анықтау болып табылады.

Бұл бағыттағы зерттеулер қирау кинетикасына тікелей физикалық тәсілдермен тіркеу бағытында жүргізіледі, яғни микроскопиялық деңгейінде қирау қирау кинетикасы зерттелінеді.

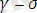
Ондай зерттеудің қажеттілігі интегралды қираудың элементар табиғатын, яғни атом деңгейінде өтетін процестерді анықтауға қажет. Себебі, ол элементар процестер u ₀ энергетикалық тосқауылдардың қасиеттерін және ол тосқауылдың шамасын анықтауға қажет болады. Шынында да, u ₀ сол дененің бастапқы энергетикалық тосқауыл әсер ететін кернеу бастапқы тосқауылды 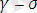-ға төмендейді. Төмендетілген тосқауылдың шамасы болады. Яғни тосқауыл жақын арақашықтықтағы жобамен бірнеше атомаралық ұзындығында орналасқан болып, сол тосқауылдан өткен кезде атомаралық байланыс қирайды деген ой-пікірді тудырады. Себебі, егер біз оншақты атомаралықтан үлкен арақашықтықта әсер ететін күшті σ кернеуді қарастырсақ, ол күштің әсері атермикалық болуы мүмкін. u ₀ -дің“атом өлшемімен ” байланыстыруға дәлел. u ₀ - дің сублимацияға тең болған себебі сублимация, яғни булану дененің бетіндегі атомдарда өтеді. Бірақ бұл қирау элементар атты нақты көптеген бір-біріне қайшы гипотезалар туады. Мысалы, [6] еңбектегі гипотезалар. Бір-біріне қарсы u ₀ қирау активация энергиясындағы бірнеше гипотезалардың барына қарамастан u ₀ -дің табиғатын зерттеуде u ₀ параметрінің бірнеше факторларға әсерін анықтау. Мысалы, кернеуленген күйдің түрін анықтау, u ₀ -дің атом-электрондық сипаттамасымен байланысын анықтау тағы басқа мәселелер. Қираудың элементар акт жолдарын табудың ең негізгі мәселесі болып табылады. Мысалы, 1950 жылдары Пинес деген ғалым денелердің қирауына ваканциялық механизммен өтеді деген гипотезаны ұсынған. Бұл механизм бойынша жүктелген денеде дене ішіндегі ваканцияның сызаттардың ұшына келуден, сызат өсіп денені қиратады. Ваканциялық механизмге негізделген теория τ-дың σ-ға, Τ-ға байланыстылығы жөнінде алынған теориялық теңдеу эксперименттен алынған теңдеуден өзгеше. Пинестің теңдеуінде exp алдындағы . 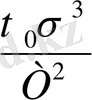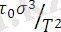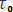Бұл теңдеу арқылы алынған жарамддылық мерзімінің эксперимент мәндерін талдау нәтижелері металдар үшінuu ₀ өздік диффузия. Бұл алынған u ₀ мәліметіне сүйене отырып, дененің элементар қирау актының табиғаты ваканциялық ой-пікірді айтуға мүмкіндік тудырады. Бірақ Пинестің exp алдындағы 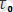күрделі параметрлер, сол параметрлерді алуға қолданған ваканционды модельге тура келетіндігіне күмән келтіреді.

Пинес u ₀ -дің өзгеруін темірден өтетін полиморфты өзгерістермен байланыстырып, яғни u ₀ -ді өздік диффузия энергиясымен байланыстырмай полиморфты энергияның өздік диффузиямен байланыстырған. Бірақ темірден өтетін полиморфты энергетикалық сипаттаманың өзгерісін анықтаудың қаншалықты дұрыс екендігіне көңіл аудармаса, ол өзгерістің мәндері бір-біріне қайшы.

Сонымен қоса, Пинестің еңбегінде темірдің жарамдылық мерзімін жоғары температурада анықтаған. ұнтақтан пісірілген кеуекті үлгілер зерттелген, ал [5-6] еңбектер нәтижелеріне сүйенсек, кеуекті пісірілген үлгілерде және жоғары температураларда ваканция концепциясы жоғары болғандықтан шынында да қирау сублимация механикасының ваканционды механизмге өтуі мүмкін.

Жоғарыда айтылған Пинестің эксперимент нәтижелерін дәлелденген мәліметтер деп айтуға болмайды. Яғни Пинестің еңбегінде u ₀ -дің қалыпты температурадағы мәні құйма металдарға анықталған сублимация энергиясына тең екендігіне күмән тудырғаны орынсыз деп есептеуге болады.

Шынында да, жоғары температурада 1/2Т _балқу және механикалық кернеу мәні төмен болған кезде 1-ші теңдеу орындалмайды. Онда болу орынды, яғни орындалған кезде 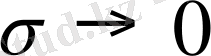жарамдылық мерзім белгілі мәнге ие болар еді, ал жоғары температурада жарамдылық мерзім өте кіші мәнге ие болар еді. Жоғары температурадағы алынған нәтижелер бірінші теңдеуге бағынбайтын себебі [6-7] еңбектерде қарастырылған.

Шынында да, [7-8] еңбекте күміске кейбір қоспаларды енгізгенде u ₀ өзгермейтіндігі және сублимация энергиясы өзгермейтіндігі анықталған. Бірақ өздік диффузия активация энергиясы елеулі өзгереді, яғни u ₀ және өздік диффузия арасында қалыпты температурада ешқандай бір мәнді байланыс жоқ екендігін көрсетеді.

Бұл бағытта u ₀ -дің кез келген процестің активация энергиясымен салыстыру дәлелді көзқарас деп есептеуге болады. Термоактивациялық талдау теориясында активация энергиясын есептеу оның мәнін феноменологиялық мәліметтермен, яғни жарамдылық мерзімінің кернеу мен температураға тәуелділігінен анықталған u ₀ -мен салыстыру тек бірдей құрылымға ие үлгілерді зерттеу кезінде орын алады. Тек осы жағдайда, яғни бірдей құрылымға ие кезде термофлуктуациялық акттың өту жылдамдығының температураға тәуелділігі қарапайым Больцман заңына бағынады. Бұл жағдайда құрылымның бірдей болуын тексеру тек үлгінің құрылым элементі анықталғаннан кейін жүргізуге болады. Тек сонда ғана ол құрылымның зерттелетін процестерге әсерін анықтауға болады.

Біз қарастыратын зерттеулерде құрылымның жарамдылық мерзімге әсерін анықтауға болады. Бірінші теңдеу арқылы u ₀ шамасын анықтау, жоғарыда көрсетілген шарттар арқылы анықтауды мынандай деп тұжырымдауға болады. Алдын-ала анықталған мәліметтерде бірінші формуладағы γ- коэффициенттің шамасын құрылым сезімтал коэффициенті деп қабылдап, белгілі күйдегі бір топ үлгілерге, атап айтқанда алдын-ала күйдіру, прокаттау дәрежесі тағы басқа өңделген үлгілердің γ- коэффициенттің мәндері бірдей деп қабылданады және әртүрлі температурада және кернеуде жылжығыштық режимде сынаған кездегі қираған үлгілері өзгермейді.

Бұрынғы жұмыстарды талдағанда гамма мен дән өлшемдері арасында байланыс бар екендігі анықталған, яғни үлгінің дән өлшемі өзгерсе гамма коэффициентінің өзгеретіні де анықталған. Бірақ металды әртүрлі темпеартурада және кернеуде жарамдылық мерзімін анықтауға зерттеу процесі барысында дән өлшемінің тұрақтылығы анықталмаған. Тек γ-ның үлгі дәнінің өлшемімен байланысы бар екендігі анықталған.

Жарамдылық мерзімге нақты құрылымның әсерін зерттеуде құрылым түрлерінің ішінде құрылым түрінің деформацияланған металдарда иондық коваленттік моно және поликристалды денелерде бірдей жалпы қасиеттерін анықтайтын құрылым түрлеріне назар аударған жөн.

Әдебиеттегі мәліметтерді талдау барысында көптеген кристалдық материалдарда блок құрылымы кездеседі, ол құрылым кристалл торында дислокацияның көлем бойынша біртексіз таралуынан келіп шығады. Жобамен блок салыстырмалы түрде дислокациясы жоқ кристалл торының бөлігін дислокация тығыздығы жоғары бөлігінің шекарасын көрсетеді. Сонымен қатар блок шекарасындағы бір таңбалы дислокациялар блоктардың орналасуында бір-бірінен бұрылу шамасын анықтайды. Ол бір таңбалы дислокациялардың концентрациясы жоғары болса, блоктың бұрылуы да жоғары.

Хирщтің ой-пікірі бойынша блоктың бұзылуы шамасы кристалдардың деформациясына, қирауына елеулі әсер етеді деп есептейміз. Бірақ қазіргі таңда блоктың бұрылу шамасы кристалдың беріктілігі мен байланыстылығын, сонымен қатар бірінші теңдеудегі γ- коэффициентімен байланысы бар екендігі зерттелмеген. Зерттелмеген себептің бірі-блок бұрылуын нақты анықтайтын тәсілді табу қиындығында, әсіресе поликристалды минералдар үшін. Әрине жарамдылық мерзімді шектейтін құрылым элементін табу өте қажет, бірақ u ₀ шамасын жан-жақты талдауға жеткіліксіз.

u ₀ -ді жеткілікті дәрежеде талдауға жүйелі түрде ол шаманың тек поликристалды металдарға ғана емес, сонымен қатар көптеген ионды, ковалентті, металдық, молекулааралық (ВДВ) әсерлесуге ие моно және поли кристалдарды зерттеуді қажет етеді. Сонымен қатар u ₀ -дің шамасына материалдың күйін анықтайтын негізгі параметрлердің, яғни қысым мен температураның әсерін білуді қажет етеді. u ₀ -ге кристалды механикалық және термикалық өңдегенде, әртүрлі қоспаларды кристалға енгізгенде, фазалардың бөлінуі, аллатропиялық өтулер арқасындағы кристалл құрылымының өзгеруі u ₀ шамасына әсерін анықтауды қажет етеді.

Шынында да, жоғарыда айтқанымыздай жарамдылық мерзімінің температураға және кернеуге тәуелділігі жөніндегі мәлімет және активация энергиясын талдауға арналған еңбектер аса көп еместігі, сонымен қатар ол мәліметтер нәтижелері бір-бірімен қайшылығы бар екендігі анықталған. Ал қирау активация энергиясын анықтағанда материалдардың құрылымы жөнінде зерттеулер жасалынбаған.

Бұл бағытта тек феноменологиялық зерттеу жүргізу жеткіліксіз. Бірақ материалдардың қирау кинетика табиғатын талдауда, дәлелдеуде қажетті мәліметтерді береді. Ол мәліметтерді нақтылау мақсатында тікелей физикалық тәсілдерді қолдануды қажет етеді.

Атом деңгейдегі физикалық тәсілдер микродеңгейдегі қирау элементінің пайда болуын және ол элементтердің дамуын зерттеуге мүмкіндік береді. Бұл бағыттағы зерттеулер 70-жылдары басталып, ол тәсілдер бірін-бірі толықтырады және бірін алған мәліметін бірі тексеріп отырады.

Бұл зерттеу тәсілдері негізінен қираудың бастапқы кезіндегі өтетін мәліметтерді анықтайды. Ол мәліметтер кіші өлшемдегі тұрақты сызаттардың пайда болуымен байланысты ол сызаттарды «сызат ұрығы» деп атайды. Сол микросызаттардың пайда болуын олардың өлшемдері, концентрациясы, формасы, материал көлемі бойынша өлшемдерінің таралуы материалдың жарамдылық мерзімін анықтау барысында жоғарыда айтылған сызаттардың өзгеру заңдылықтары сонымен қатар қирауға қарама-қарсы микросызаттардың емделу процестерін зерттеуді қажет етеді.

Металдар мен кристалдарда микросызаттардың болуы соның арқасында ол кристалдардың нақты беріктілігі теориялық беріктіліктен төмен болуының себебі ертеде қарастырылған. Кристалл материалдарында сызаттардың пайда болуын пластикалық деформациясының оқшаулануымен байланыстырған .

Бұл еңбектегі идеяларды нақтылау мақсатында дислокация теориясы арқылы сызаттардың пайда болуын дәлелдеу мақсатында бірнеше механизмдер ұсынылған. Бірақ қатты денелердің ішінде микросызаттардың болу идеясы ертеде айтылмағанымен және сонымен қатар ол сызаттардың пайда болу механизмін ұсынғанмен микросызаттар жөнінде яғни олардың пайда болуы және дамуы жөнінде эксперименталдық мәліметтер жоқтың қасы. Сондықтан жоғарыдағы айтылған бастапқы қирау кездегі заттың пайда болуы және дамуы зерттелмеген.

Зерттелмеудің бірден-бір себебі, микросызатты көру тәсілдерінің қиындығы мен күрделілігінде деп есептеуге болады. Дегенмен, қазіргі кездегі кездесетін микросызатты анықтайтын мәліметтерге тоқталайық.

Микрон және одан да үлкен әрбір сызаттар [8] еңбектерде пайда болуын дислокациялық механизммен қарастырылған болса, оларды эксперимент арқылы көру ионды LiFжәне MgO кристалдарда В. Н. Рожанскийдің және т. б. ғалымдардың еңбектерінде анықталған.

Р. И. Гарберд, И. В. Обреимов, Л. М. Поляков еңбектерінде бірнеше тәсілдермен, атап айтқанда жарық сәулесінің шашырауы, электрондық микроскопия және тығыздықты өлшеу тәсілдерімен бөлме температурасын (18 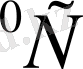температурада) NaCl кристалында оны қысқан кезде пайда болған микросызаттар зерттелген. Зерттеу нәтижелеріне қарағанда деформацияның басында-ақ үлгінің көлемінде 200-ден 1000 Å өлшем аралығында сызаттар пайда болғаны анықталған. Бірақ бұл сызаттардың концентрациясы, олардың жинақталуы және бастапқы қирау кезіндегі басқа да мәліметтер бұл еңбектерде қарастырылмаған. Сондықтан жарық сәулесінің кристалда шашырауын микросызатпен байланыстыру біршама күмән тудырады. Ол жөнінде Н. И. Абаев, Н. И. Корнфельт сияқты зерттеушілер ескерткен.

И. А. Одюнг, Ю. П. Либеров еңбектерінде электрондық микроскопия және тығыздықты электрокедергіні өлшеу арқылы бөлме температурасында поликристалды никель, мыс, алюминий, темір металдарын бір бағытта созған кезде пайда болған микросызаттар анықталған. Алынған мәліметтерге қарағанда зерттелген материалдардың деформациясы қираған кездегі деформациямен жобамен 20-30% деформациясына жеткен кезде металдар ретінде ұзындығы 2-7 мкм және ені 0, 1 мкм микросызаттар пайда болғаны анықталған. Бірақ жоғарыда айтқанымыздай ол сызаттардың қирау басталғандағы концентрациясы, олардың жинақталуы және басқа да мәліметтер анықталмаған.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.