Гармониялық тербелістің энергиясы

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 61 бет
Таңдаулыға:

Қазақстан Республикасы Білім және ғылым министрлігі

Қ. А. Ясауи атындағы Халықаралық Қазақ-Түрік университеті

Жаратылыстану факультеті

Кибишева Б

Тақырыбы: Атомдық, молекулалық және ядролық физикада гармониялық осциллятор теориясын қолдану

ДИПЛОМДЫҚ ЖҰМЫС

050604-мамандығы - «Физика»

Түркістан 2010ж

Қазақстан Республикасы Білім және ғылым министрлігі

Қ. А. Ясауи атындағы Халықаралық Қазақ-Түрік университеті

Жаратылыстану факультеті

«Қорғауға жіберілді»

Физика кафедрасының меңгерушісі

ф. -м. ғ. д., профессор Бақтыбаев А. Н

«» 2010ж

ДИПЛОМДЫҚ ЖҰМЫС

Тақырыбы: Атомдық, молекулалық және ядролық физикада гармониялық осциллятор теориясын қолдану

050604-мамандығы бойынша - «Физика»

Орындаған: Б. Кибишева

Ғылыми жетекшісі: физ-мат. ғ. к. Б. Бекмурзаев

Түркістан 2010ж

Мазмұны

Кіріспе . . . 4

I тарау . Тербелістер туралы жалпы мәліметтер . . . 6

Гармониялық тербелістер . . . 6
Гармониялық тербелістің энергиясы . . . 10
Гармониялық осциллятор . . . 11
Системаның тепе-теңдік қалпының маңындағы болымсыз тербелістері . . . 14
Математикалық маятник . . . 15

II тарау. Атомдық, молекулалық және ядролық физикада гармониялық осциллятор теориясын қолдану . . . 17

Сызықты гармониялық осциллятор . . . 17
Сызықты гармониялық осциллятордың кванттық энергиясы . . . 20
Сызықты осциллятордың қалыпты және қозған күйі . . . 23
Өзара байланысқан осцилляторлар. Ван-дер-Ваальс күштері . . . 28
Үш өлшемді потенциал жәшіктегі бөлшек . . . 33
Сызықты гармониялық осциллятордың теориялық физикада қолданылуы . . . 36
Бірөлшемді қозғалыс теңдеуінің жалпы қасиеттері . . . 41

ІІІ тарау. Кванттық механика және Шредингер теңдеуі . . . 45

3. 1. Шредингер теңдеуі . . . 45

Шрадингер теңдеуі және кванттау . . . 48
Гармониялық осциллятор . . . 51
Бірөлшемді потенциалдық шұңқырлар . . . 53
Гамильтон теңдеуі. Фазалық кеңістік . . . 58

Қорытынды . . . 62

Пайдаланылған әдебиеттер . . . 64

КІРІСПЕ

Гармониялық осциллятор кванттық-механикалық есептерді шешуде қолданатын модель. Гармониялық осциллятор өзінің симметрия қасиетімен көптеген физиканың есептерінде кездеседі. Осциллятор теориясын жасау үлкен практикалық маңызы бар. Себебі, көптеген есептерді шешкен кезде Шредингер теңдеуін қолданамыз. Біздің жұмысымызда гармониялық осциллятор атомдық, молекулалық және ядролық физикада қолданылуын көрсету болып табылады.

Тербелістер деп белгілі бір дәрежеде қайталағыштығымен айқындалатын процесстерді айтады. Мысалы, сағат маятнигінің тербелуі, ішектің немесе камертон таяқшасының тербелісі, радиоқабылдағыш контурының конденсатор астарларындағы кернеу және т. б. осындай қайталағыштық қасиетке ие болады.

Қайталанатын процесстің физикалық табиғатына байланысты тербелістер: механикалық, электромагниттік, электромеханикалық және т. б. түрге бөлінеді.

Тербелістер табиғат пен техникада кеңінен таралған. Көптеген жағдайда олар зиянды роль атқарады. Рельс арқылы поэзд дөңгелегінің өтуі кезіндегі соққы салдарынан пайда болатын көпірдің тербелісі, еспе винттің айналуы салдарынан корабль қорабының тербелісі (вибрациясы), самолет қанаттарының вибрациясы тәрізді процестер апатқа ұшыратуы мүмкін. Мұндай жағдайда міндет - тербелісті алдын ала болдырмау немесе ең болмағанда тербелісті қауіпті мөлшерге жеткізбеу.

Сонымен қатар, тербелмелі процестер техниканың түрлі салаларының негізін қалайды. Мысалы, бүкіл радиотехника тербелмелі процестерге негіздеоген.

Тербелмелі системаға жасалатын әсердің сипатына қарай еркін (немесе меншікті) тербелістер, еріксіз тербелістер, автотербелістер және параметрлік тербелістер болып ажыратылады.

Еркін немесе меншікті тербелістер деп қозғалысқа келтірілгеннен кейін немесе орнықты қалпынан шығарылғаннан соң өзімен-өзі қалатын системада өтетін тербелістарді айтады. Жіпке ілінген шариктің (маятник) тербелісі осыған мысал бола алады. Қозғалысты тудыру үшін шарикті түртіп жіберу керек немесе оны бір жағына тартып апарып қоя беру керек.

Еріксіз тербелістер деп тербелмелі система әлсін-әлі өзгеріп отыратын сыртқы күштің әсеріне кез болатын тербелістерді; алайда бұл әсерлер жүзеге асатын уақыт мезетінде тербелмелі системаның өзі белгілейді - сыртқы әсерлерді системаның өзі басқарады. Жоғары көтерілген гирдің немесе бұралған пружинаның энергиясы есебінен маятнигі түрткі алатын (қозғалысқа келетін) сағат осыған мысал бола алады. Бұл түрткілер маятник ортаңғы қалпынан өтер кезде беріледі. Параметрлік тербелістер кезінде сыртқы әсер салдарынан системаның қандай да болсын параметрі, мысалы, тербеліс жасап тұрған шарик ілінген жіптің ұзындығы, периодты түрде өзгереді.

Гармониялық тербелістер, яғни тербелетін шама (мысалы, маятниктің ауытқуы) уақыт бойынша синус не косинус заңына сәйкес өзгеретін тербелістер қарапайым тербелістер қатарына жатады. Бұл тербелістер мына себептерден есе маңызды деп саналады: біріншіден табиғаттағы және техникадағы тербелістер көбінесе гармониялық тербелістерге жақын сипатта болады, және екіншіден басқа түрдегі периодты процестерді (уақытпен басқаша тәуелділікте болатын) бірнеше гармониялық тербелістердің қосылуы ретінде қарастыруға болады.

Гармониялық осциллятор тепе-теңдік қалыптың маңында гармониялық тербеліс жасайтын, система болып табылады. m массалы бөлшек тепе-теңдік жағдайдан ауытқуға пропорционал және бағыты тепе-теңдік күйге бағытталған күш әсерінен қозғалсын дейік. Мұндай тербелістік жүйе сызықты гармониялық осциллятор деп аталады. Бұған мысал ретінде серпімді пружинаға ілінген ауыр шарды алсақ болады. Электр өрісінің әсерінен тербелетін электрон сызықты гармониялық осциллятор бола алады. Өріс әсерінен қозғалатын электронға әсер етуші күш тепе-теңдік күйінен ауытқуының бірінші дәрежесіне пропорционал және осы тепе-теңдік күйге қарай бағытталады.

І тарау. Тербелістер туралы жалпы мәліметтер

1. 1. Гармониялық тербелістер

Пружинаға ілінген, массасы m шариктен тұратын системаны қарастырайық (1-сурет) . Тепе-теңдік күйінде mg күші k∆l ₀ серпімділік күшімен теңгеріледі.

(1. 1)

Шариктің тепе-теңдік қалпынан ығысуын х координатасымен сипаттаймыз, әрі х осін вертикаль бойымен төмен бағыттаймыз, ал осьтің нолін шариктің тепе-теңдік қалпымен үйлестіреміз.

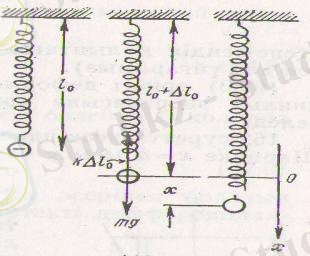
1-сурет. Пружинаға ілінген, массасы m шариктен тұратын система.

Егер шарикті тепе-теңдіктен х -қа ( х алгебралық шама) тең қашықтыққа ығыстырсақ, онда пружинаның ұзаруы ∆ l ₀ +x шамасына тең болады және қорытқы күштің х осіне проекциясы (бұл проекцияны жай ғана f әрпімен белгілейік) мынадай мән қабылдайды:

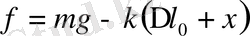
(1. 1) формуласындағы тепе-теңдік шартын ескере отырып, төмендегіні аламыз:

(1. 2)

(1. 2) формуласындағы «-» ығысу мен күштің бағыттары қарама қарсы екендігін білдіреді: егер шариктің тепе-теңдік қалпынан төмен қарай ( x>0 ) ығысса, күш жоғары ( f<0 ) бағытталады, шарик жоғары қарай ( x<0 ) ығысқанда күш төмен ( f>0 ) бағытталады. Сонымен f күшінің төмендегідей қасиеттері бар: 1) ол шариктің тепе-теңдік қалпынан ығысуына пропорционал, 2) ол әрқашанда тепе-теңдік қалпына қарай бағытталған.

Біз қарастырған мысалда (1. 2) күш шынында да, өзінің табиғаты бойынша серпімді. Басқа тектегі күштерде де осындай заңдылық байқалуы мүмкін, яғни - kx шамасына тең болуы мүмкін, мұндағы k - тұрақты оң шама. Табиғатына қарамастан, мұндай күштерді квазисерпімді деп атау келісілген.

Системаға х ығысу беру үшін, квазисерпімді күшке қарсы төмендегідей жұмыс істеуі керек:

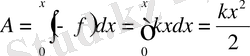Бұл жұмыс системаның потенциялдық энергиясының қорын жасауға жұмсалады. Демек, квазисерпімді күш әсер ететін, система, тепе-теңдік қалпынан х қашықтыққа ығысқанда төмендегідей потенциялдық энергияға ие болады (тепе-теңдік қалыптағы потенциялдық энергияны нольге тең деп ұйғарамыз) :

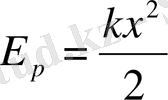(1. 3)

(1. 3) өрнегі деформацияланған пружинаның потенциялдық энергиясына арналған 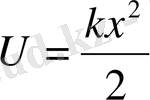өрнегіне сәйкес келеді.

1-суретте кескінделген системаға қайта оралайық. Шарикке x=a ығысу беріп, одан соң системаны өзімен-өзін қалдырайық. f=kx күшінің әсерінен шарик тепе-теңдік қалыпқа қарай үнемі артып отыратын жылдамдықпен қозғалады. Бұл кезде системаның потенциялдық энергиясы кеми бастайды (2-сурет), бірақ оның орнына үнемі артып келе жатқан кинетикалық энергия 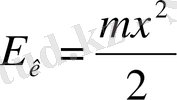пружинаның массасын ескермейміз) пайда болады. Тепе-теңдік қалпына келген соң шарик, инерция бойынша қозғала береді. Бұл қозғалыс кемімелі қозғалыс болады және кинетикалық энергия толығымен потенциялдық энергияға айналғанда, яғни шариктің ығысуы - а -ға тең болғанда тоқталады. Одан соң шарик кері бағытта қозғалғанда дәл осындай процестер өтеді. Егер системада үйкеліс болмаса, системаның энергиясы сақталуға тиіс және шарик x=a -дан x=-a -ға дейінгі аралықта шексіз ұзақ қозғала береді.

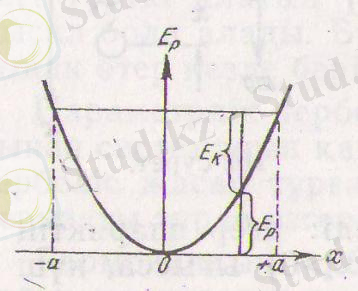
2-сурет. Системаның потенциялдық энергиясының кемуі.

Шарикке арналған Ньютонның екінші заңы былай жазылады:

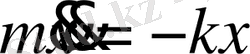Бұл теңдеуді төмендегідей етіп түрлендірейік:

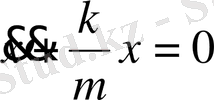(1. 4)

х -тағы коэффициент оң. Сондықтан оны мынадай түрде жазуға болады:

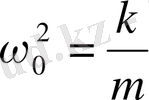(1. 5)

мұндағы 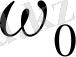- заттық шама.

(1. 4) өрнегіне (1. 5) өрнегіндегі белгілеуді қолдана отырып, мынаны аламыз:

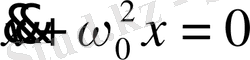(1. 6)

Сонымен, (1. 2) түріндегі күштің әсерінен болатын шарик қозғалысы екінші реттік біртекті дифференциалдық теңдеулер арқылы зерттеледі.

Ауыстыру арқылы (1. 2) теңдеуінің жалпы шешімі төмендегідей болатындығына оңай көз жеткізуге болады:

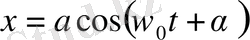(1. 7)

мұндағы а және α - кез келген тұрақты шамалар. Сонымен х ығысу уақыт бойынша косинус заңына сәйкес өзгереді. Демек, f=-kx түріндегі күштің әсерінде болатын системаның қозғалысы гармониялық тербеліс болып табылады.

Гармониялық тербеліс, яғни (1. 7) функциясының графигі 3-суретте көрсетілген. Горизонталь оське t уақыт, ал вертикаль оське х ығысу салынған. Косинус -1-ден +1-ге дейін өзгеретіндіктен, х -тің мәні - а -дан + а -ға дейінгі аралықта жатады.

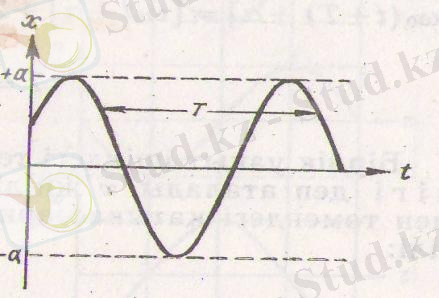
3-сурет. Гармониялық тербелістің графигі.

Системаның тепе-теңдік қалпының ең үлкен ауытқуы тербеліс амплитудасы деп аталады. Тербеліс амплитудасы а - тұрақты оң шама. Оның мәні, системаны тепе-теңдік қалыптан шығарған, алғашқы ауытқудың немесе түрткінің шамасымен анықталады.

Косинус таңбасының астында тұрған 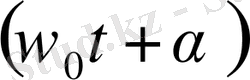шамасы тербеліс фазасы деп аталады. Α тұрақтысы фазаның t=0 уақыт мезетіндегі мәні болып табылады және ол тербелістің бастапқы фазасы деп аталады. Санау уақытының басы өзгергенде де өзгереді. Демек, бастапқы фаза санау уақытының басын таңдап алуға байланысты өзгереді. 2π бүтін санын фазаға қосқанда немесе одан алып тастағанда х -тің мәні өзгермейтіндіктен, бастапқы фазаны модулы бойынша әрқашан да π-ден кіші деп алуға болады. Сондықтан, көбінесе, α-ның -π-ден +π-ге дейінгі аралықта жатқан мәндері ғана қарастырылады.

Косинус - периоды 2 π-ге тең периодты функция болғандықтан, гармониялық тербеліс жасайтын системаның әр түрлі күйі тербеліс фазасы 2π- ге тең өсімше қабылдайтындай Т уақыт аралығы сайын қайталанады (2-сурет) . Осы Т уақыт аралығы тербеліс периоды деп аталады. Оны төмендегі шарттан анықтауға болады:

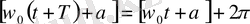осыдан

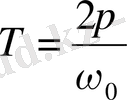(1. 8)

Бірлік уақыт ішіндегі тербеліс саны ν тербеліс жиілігі деп аталады. ν жиіліктің бір тербеліс ұзақтығымен төмендегі қатынас арқылы байланысатындығы белгілі:

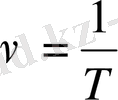(1. 9)

Жиілік бірлігі үшін периоды 1 сек -ке тең тербеліс жиілігі алынады. Бұл бірлікті герц ( гц ) деп атайды. 10 ³ гц жиілік килогерц ( кгц ), 10 ⁶ гц - мегагерц ( мгц ) деп аталады.

(1. 8) өрнегінен төмендегіні алуға болады:

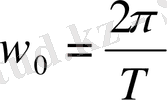(1. 10)

Сонымен, 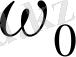шамасы 2 π секунд ішіндегі тербеліс санын береді. 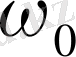шамасын дөңгелектік немесе циклдік жиілік деп атайды. Ол әдеттегі ν жиілікпен төмендегі қатыс арқылы байланысады:

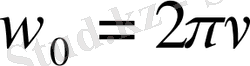(1. 11)

(1. 7) өрнегі уақыт бойынша дифференциалдап, жылдамдыққа арналған өрнекті аламыз:

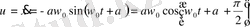(1. 12)

(1. 12) өрнегінен, жылдамдық та гармониялық заң бойынша өзгеретіндігін әрі жылдамдық амплитудасы 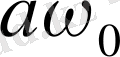шамасына тең болатындығын көреміз. (1. 7) және (1. 12) өрнектерін салыстырудың жылдамдық ығысудан фазасы бойынша 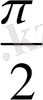шамасына озып кететіндігі шығады.

(1. 12) өрнегін тағы да уақыт бойынша дифференциалдап, үдеуге арналған өрнекті табамыз:

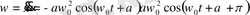(1. 13)

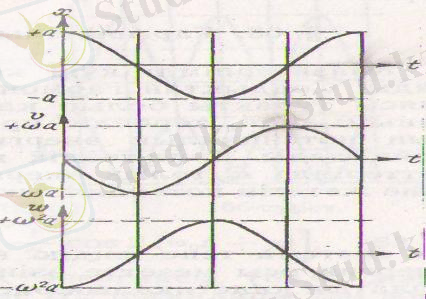
4-сурет. Ығысу, жылдамдық және үдеуге арналған график.

(1. 13) өрнегінен үдеу мен ығысу қарама-қарсы фазада жататындығы көрінеді. Мұның өзі ығысу ең үлкен оң мәніне жеткенде, үдеудің шама жағынан ең үлкен теріс мәніне жететіндігін және керісінше болатындығын көрсетеді.

4-суретте ығысу, жылдамдық және үдеуге арналған графиктер келтірілген.

Әрбір нақты тербеліс а амплитуда мен бастапқы фазаның белгілі бір мәні бойынша сипатталады. Берілген тербеліс үшін бұл шамалардың мәндері бастапқы шарттардан, яғни х ₀ ауытқу және уақыттың бастапқы мезетіндегі жылдамдықтың мәндерінен анықталады.

Шынында да, (1. 7) және (1. 12) өрнектеріндегі t=0 деп ұйғарып, екі теңдеу аламыз:

, ,

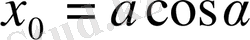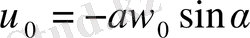осылардан төмендегіні табамыз:

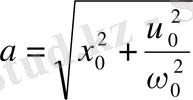(1. 14)

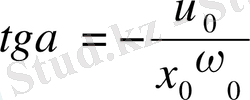(1. 15)

Α-ның -π-ден +π-ге дейінгі интервалда жатқан екі мәні (1. 15) теңдеуін қанағаттандырады. Бұл мәндерден косинус пен синустың таңбасы дұрыс болатын мәнді алу керек.

Гармониялық тербелістің энергиясы

Квазисерпімді күш консервативті күш болып саналады. Сондықтан гармониялық тербелістің толық энергиясы тұрақты болып қалуы керек. Жоғарыда айқындағанымыздай, тербеліс процесінде кинетикалық энергияның потенциалдық энергияға және керісінше түрленуі байқалады. Тепе-теңдік қалыптан ең үлкен ауытқу мезеттерінде Е толық энергия, өзінің Е _pmax ең үлкен мәніне жететін потенциалдық энергиядан ғана тұрады:

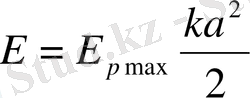(1. 16)

Ал система тепе-теңдік қалып арқылы өткенде толық энергия осы мезетте өзінің ең үлкен E _kmax мәніне ие болатын кинетикалық энергиядан ғана тұрады:

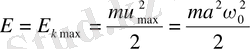(1. 17)

(жоғарыда жылдамдық амплитудасы 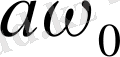шамасына тең болатындығы көрсетілген) . (1. 5) өрнегі бойынша 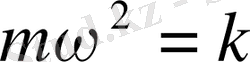болатындықтан, (1. 5) және (2. 2) өрнектерінің бір-біріне тең екендігі оңай байқалады.

Гармониялық тербелістің Е _к кинетикалық және Е _р потенциалдық энергиялары уақыт бойынша қалай өзгеретінін айқындайық.

Кинетикалық энергия [ х үшін (1. 12) өрнегін қараңыз] төмендегі өрнек арқылы анықталады:

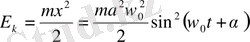(1. 18)

Потенциалдық энергия мына формуламен өрнектеледі:

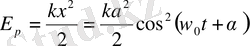(1. 19)

(1. 18) және (1. 19) өрнектерін (1. 5) қатысын ескере отырып қоссақ, төмендегіні аламыз:

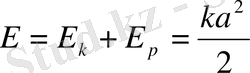(немесе 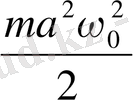) (1. 20)

бұл (1. 16) және (1. 17) өрнектерімен сәйкес келеді. Сонымен гармониялық тербелістің толық энергиясы шынында да тұрақты болады екен.

Тригонометриядағы белгілі формулаларды пайдаланып, Е _к және Е _р шамаларына арналған өрнектерді мына түрде жазуға болады:

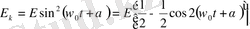(1. 21)

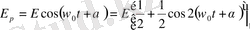(1. 22)

мұндағы Е системаның толық энергиясы. (1. 21) және (1. 22) формулаларынан Е _к және Е _р шамалары 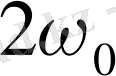жиілікпен, яғни гармониялық тербеліс жиілігінен 2 есе артық жиілікпен өзгеретіндігі көрінеді. 5-суретте х, Е _к , Е _р шамаларының графиктері салыстырмалы түрде берілген. Синустың квадраты мен косинустың квадраттарының орташа мәні жартыға 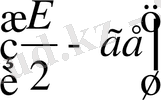тең екендігі белгілі. Демек, Е _к шамасының орташа мәні Е _р шамасының орташа мәнімен сәйкес келеді және ол Е/2 -ге тең.

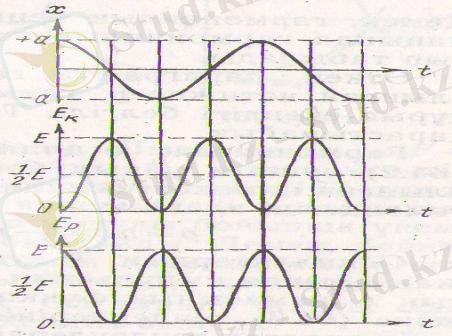
5-сурет. х, Е _к , Е _р шамаларының графиктері.

Гармониялық осциллятор

Гармониялық осциллятор тепе-теңдік қалыптың маңында гармониялық тербеліс жасайтын, система болып табылады.

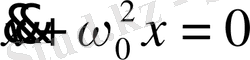(1. 23)

мұндағы 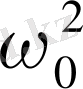- тұрақты оң шама [(1. 6) формуласын қараңыз], теңдеуімен сипатталған система гармониялық осциллятор (немесе гармониялық вибратор) деп аталады.

(1. 23) теңдеуінің шешімі төмендегідей түрде жазылатындығы бізге бұрыннан белгілі:

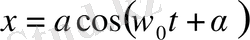(1. 24)

Жоғарыда айтылғандай гармониялық тербелістер үшін алынған нәтижелер, гармониялық осциллятор үшін де дұрыс екендігі белгілі. Тағы да екі мәселені қосымша қарастырайық.

Гармониялық осциллятордың импульсін табайық. (1. 24) өрнегін уақыт бойынша дифференциалдап және алынған нәтижені осциллятордың m массасына көбейтіп, төмендегіні аламыз:

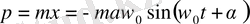(1. 25)

Осциллятордың х ауытқуымен сипатталатын әрбір жағдайында импульстің кейбір р мәні болады. р шамасын х шамасының функциясы ретінде табу үшін (1. 24) және (1. 25) теңдеулерінен t уақытты шығару керек. Ол үшін аталған теңдеулерді мына түрде жазайық:

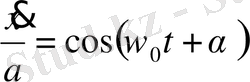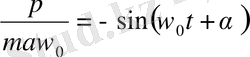Бұл өрнектерді квадраттап және қосу арқылы мынаны аламыз:

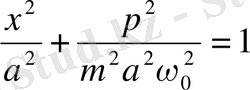(1. 26)

6-суретте гармониялық осциллятордың р импульсінің х ауытқуға тәуелділігің графигі кескінделген.

р, х координата жазықтығын фазалық жазықтық деп, ал оған сәйкес келетін графикті фазалық траектория деп атайды. (1. 25) формуласымен сәйкес гармониялық осциллятордың фазалық траекториясы жарты осьтер а және 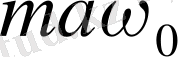болатын эллипс болып табылады.

Фазалық траекторияның әрбір нүктесі х ауытқуды және р импульсті, яғни уақыттың кейбір мезетіндегі оциллятордың күйін кескіндейді. Уақыт өткен сайын күйді кескіндейтін нүкте (қысқаша оны бейнелеуші нүкте деп атайды) фазалық траектория бойымен қозғала отырып, тербеліс периоды ішінде оны толық бір айналып шығады.

Бейнелеуші нүктенің қозғалысы сағат тілінің қозғалысы бойынша бағытталатындығына оңай көз жеткізуге болады. Шынында да, 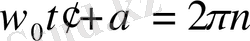( n - бүтін сан) болатын 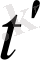уақыт мезетін алайық. Бұл уақыт мезетіне x=a және p=0 (6-суреттегі 1 нүктесін қараңыз) сәйкес келеді. Одан арғы уақыт мезеттерінде х кеми береді, ал р модулы бойынша үнемі өсіп отыратын теріс мәндер қабылдайды. Демек, бейнелеуші нүкте 6-суретте стрелкамен көрсетілген бағытта, яғни сағат тілінің қозғалысы бойынша қозғалады.

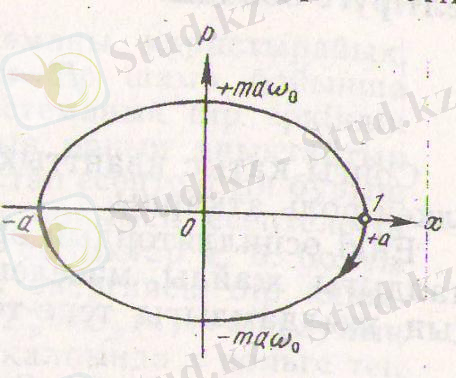
6-сурет. Гармониялық осциллятордың р импульсінің х ауытқуға тәуелділігі.

Эллипстің ауданын табайық. Ол эллипс жарты осьтерінің π-ге көбейтіндісіне тең екендігі белгілі:

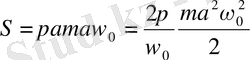
(1. 20) формуласы бойынша 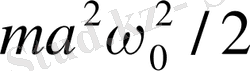осциллятордың толық энергиясы; 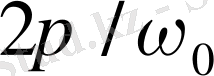шамасы 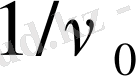-ге тең, мұндағы 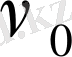- берілген осциллятор үшін тұрақты шама болып саналатын осциллятордың меншікті жиілігі.

Демек, эллипстің ауданын мына түрде бере алады:

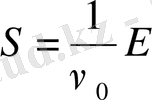бұдан,

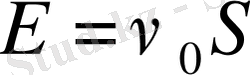
Сонымен гармониялық осциллятордың толық энергиясы эллипстің ауданына пропорционал болады, әрі пропорционалдық коэффициентін осциллятордың меншікті жиілігі атқарады.

Эллипстің ауданын 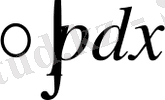интегралы ретінде есептеуге болады. Сондықтан (1. 20) формуласын мынадай түрге келтіруге болады.

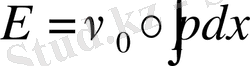
Соңғы қатыс кванттық механиканың негізін жасауда үлкен роль атқарады.

Енді осциллятордың әр түрлі қалыпта байқалу ықтималдығы жайлы мәселені қарастырайық. Осциллятордың жылдамдығы тепе-теңдік қалпынан өткен мезетте ең үлкен мәніне жетеді. Тепе-теңдік қалыптан ең үлкен ауытқыған мезетте жылдамдық нольге айналады.

Осыдан, осцилляторды өзінің шеткі қалыптарының бірінде байқау ықтималдығы, оны тепе-теңдік қалпының маңынан байқау ықтималдығынан артық болады. Бұл жағдай ықтималдық тығыздығы деп аталатын 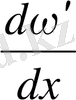шамасын анықтайтын қисық сызық кескінделген 7-сурет арқылы түсіндіріледі.

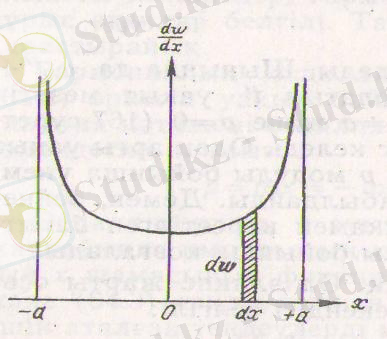
7-сурет. Ықтималдық тығыздығы деп аталатын 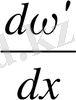шамасын анықтайтын қисық сызықтың кескіні.

Осциллятордың берілген 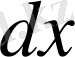аралығында болу 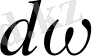ықтималдығын табу үшін, сәйкес жердегі қисық сызықтың ординатасын 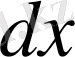шамасына көбейту керек. Мәселен, 7-суреттегі штрихталған жолақтардың сан жағынан осциллятордың берілген 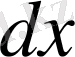интегралының шегінде табылатын 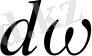ықтималдығына тең болады. Ықтималдық тығыздығы қисықтығының астындағы бүкіл аудан осциллятордың - а -дан + а -ға дейінгі шектеріндегі орындарының бірінде болғандығы ықтималдықты береді, демек, кез келген ең анық оқиғаның ықтималдығы ретінде бірге тең болуы тиіс.

Гармониялық осциллятордың әр түрлі қалпы үшін кванттық механика бір-бірінен алшақ түрліше нәтиже беретінін айтып өтейік.

Системаның тепе-теңдік қалпының маңындағы болымсыз тербелістері

Кез келген механикалық системаны қарастырайық, оның орны х арқылы белгіленетін бір шама бойынша берілуі мүмкін, бұл жағдайда ситеманың бір еркіндік дәрежесі бар делінеді.

Системаның орнын анықтайтын х шамасы кейбір жазықтықтан бастап есептелетін бұрыш немесе берілген қисық сызықтың бойымен есептелетін қашықтық, атап айтқанда, түзу, сызықтар т. б. болуы мүмкін. Системаның потенциялдық энергиясы бір айнымалы х -тің функциясы болады: 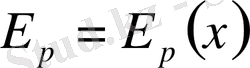. Санаудың басы х -ті, системаның тепе-теңдік қалпында х нольге тең болатындай етіп аламыз. Онда 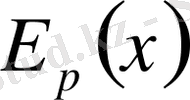функциясының x=0 болғанда минимумы болады. 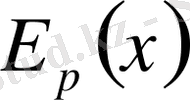функциясын х -тің дәрежесі бойынша қатарға жіктейміз, сонымен қатар х -тің жоғарғы дәрежелерін ескермеуге болатындай әлсіз тербелістерді қарастырумен шектелмекпіз.

Маклерон формуласы бойынша

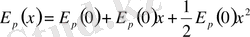
( х аз болғандықтан қалған х мүшелерін ескермейміз) .

x=0 болғанда 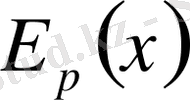функциясының минимумы болатындықтан да 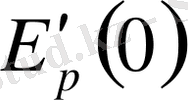нольге тең, ал 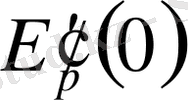оң. Мынадай белгілеу енгізейік:

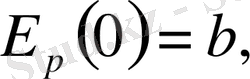
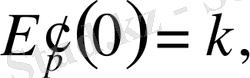( k>0 ) .

Сонда

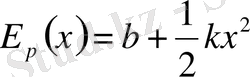(1. 27)

(1. 27) өрнегі квазисерпімді күш әсер ететін ( b константасын нольге тең деуге болады) системаның потенциалдық энергиясына арналған (1. 3) өрнегімен бірдей. 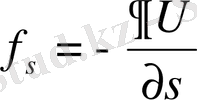қатысын пайдаланып, системаға әсер ететін күшті табуға болады:

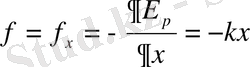
Сонымен тепе-теңдік қалыптан болымсыз ауытқу кезіндегі потенциалдық энергия ығысудың квадраттық функциясы, ал системаға әсер ететін күш квазисерпімді күштің түріндей болады.

Демек, тепе-теңдік қалыптан болымсыз ауытқу кезінде, кез келген механикалық система гармониялық тербеліске жақын тербеліс жасайды.

Математиаклық маятник

Математиаклық маятник деп салмақсыз және созылмайтын жіпке ілінген, массасы бір нүктеге жинақталған идеалданған системаны айтады. Ұзын жіңішке жіпке ілінген шағын ауыр шарик едәуір дәрежеде математиаклық маятникке жақындайды.

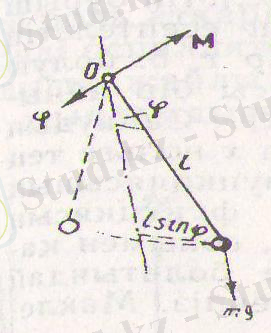
8-сурет. Маятниктің тепе-теңдік қалыптан ауытқуы.

Маятниктің тепе-теңдік қалыптан ауытқуын жіптің вертикальмен жасаған бұрышы арқылы сипаттаймыз (8-сурет) . Маятник тепе-теңдік қалыптан ауытқыған кезде шама жағынан mglsinφ -ге тең ( т - маятниктің массасы, ал l - оның ұзындығы) айналдырушы мезет пайда болады. Ол маяникті тепе-теңдік қалпына келтіруге тырысатындай болып бағытталады және бұл жағынан квазисерпімді күшке ұқсас. Сондықтан, ығысу мен квазисерпімді күш тәрізді М моменті мен бұрыштық ығысуына қарама-қарсы жазу керек.

Демек, айналмалы моментке арналған өрнек мына түрде жазылады:

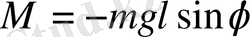(1. 28)