Тікбұрышты және қиғашбұрышты сфералық үшбұрыштардың теориясы мен есептеу әдістері


Мазмұны
Кіріспе . . .
І - Тарау. Тікбұрышты сфералық ұшбұрыш . . .
1. 1 Сфералық тригонометрияның негізгі формулалары . . .
1. 2 Тікбұрышты сфералық үшбұрыштарды шешу . . .
ІІ - Тарау. Қиғашбұрышты сфералық үшбұрыш . . .
- Қиғашбұрышты сфералық үшбұрышты шешу формулалары . . .
- Қиғашбұрышты сфералық үшбұрыштарды шешу . . .
Қорытынды . . .
Кіріспе
Сфералық тригонометрия, сферлалық үшбұрыштардың метрикалық қасиеттері мен есептеу жолдарының әдістерін үйрететін сфералық геоетрияның бөлігі болып табылады. Сфералық үшбұрыш, сфералық көпбұрыштарды бөліктерге бөлу арқылы алынатын элементар фигура.
Бастапқыда ежелгі дәуір мен ортағасыр ғылымының бір бөлігі болған сфералық тригонометрия, астрономия ғылымының сұраныстарынан пайда болып, дамыған. Оның дамуының жаңа стимулы XVII ғасырда геодезия, картография мәселелері мен теңізде жүзу сұраныстарына байланысты.
Көрінетін аспан денелерінің қозғалысын үйрене отырып, ежелгі асторномдар оларды аспан сферасында болып жатқан құбылысдеп, шындығында да бар, Жерді қоршап жатыр деп қарастырған. Ежелгі грек математигі Евдокс Книдский (б. з. д. IV ғ. ) зерттелінп отырған: Ай, Күн, планеталар және жұлдыздардың қозғалыстарын жай құрамдарға бөліп, олардың кинематикасын, Жердің ортасынан өтіп, бір - бірімен әртүрлі бұрыш жасап қиылысатын, өстер атырабында бірқалыпты айналатын 27 концентрлі сфералар көмегімен сапалы түрде көрсетті.
Ежелгі ұлы астроном Гиппарх (б. з. д. II ғ. ) өзінің «Феномена» трактатында аспан сферасының ғажайып нүктелері мен шеңберлерін және сферада сандық есептерді толықтыру үшін қажет болатын шеңбер хордасының шамаларының кестесін құрып, сфера жайлы түсінікті қалыптастырғандардың бірі болған. Менелай Александрийский (б. з. I ғ. ) өзінің «Хордаларды есептеу жайлы» және «Сферика» кітаптарында, бір немесе екі үшбұрыштың бұрыштары мен қабырғаларының теңдігін, теңсіздігін біртіндеп қарастырады. Ал Клавдий Птоломей ( б. з. II ғ. ) атақты «Алмагест» еңбегінде сфералық үшбұрыштар жайлы бірнеше теоремалардың дәлелдеулерін келтіріп, 0° арқылы есептелінген шеңбер доғасының жаңа кестесін көрсетті.
Орта ғасырларда нақты ғылымды дамытуды араб ғалымдары қолға алды. Бағдат математигі Әль - Баттани (850 - 929 ж. ж. ) тригонометриялық функция «синусты» қолдана отырып, жаңа тригонометриялық функция - тангенсті алады.
Әзербайжан математигі Насирәддин Гузи (1201 - 1274 ж. ж. ) бірінші болып сфералық тригонометрияны өз бетінше ғылым дисциплинасы ретінде қарастырды. Ол сфералық үшбұрыштың берілген үш бұрышы арқылы, берілген ұшбұрышқа поляр болған - көмекші үшбұрышты салу көмегімен қабырғасын анықтау есебін шығарды.
Қайта өрлеу заманында европалық математиктер арасында сфералық тригонометрия мәселелерімен Пурбах (1423 - 1461 ж. ж. ) пен Региомонтан (1436 - 1476 ж. ж. ) айналысқан. Пурбах сфералық үшбұрыштарды есептеуге арналған бірнеше формулаларды шығарды және 10' бұрыш арқылы синустардың жаңа кестесін есептейді. Региомонтан сфералық тригонометрия дамуына бай үлесін қосты. Грек, араб шығу көздеріне сүйене отырып, ол синус пен косинус теоремаларын дамытады және сфералық үшбұрыштарды есептеудің әртүрлі жағдайларын қарастырды.
Сфералық тригонометрияға қазіргі заманға сай көрініс берген Эйлер (1707 - 1783 ж. ж. ) . Ол қабырғалары мен бұрыштары 180°-тан кіші болған үшбұрыштарды қарастырды. Осының көмегімен ол сфералық тригонометрияның көптеген формулаларын пайдалануды жеңілдетті.
Сфералық тригонометрияның практикалық қосындыларында Лаагранж теоремасы үлкен мәнге ие. Соның көмегімен кіші сфералық үшбұрыштарды есептеуде дәлдікті жоғалтпай жазықтық тригонометрия формуласы бойынша жасап шығарды.
ХХ ғасырда сфералық тригонометрияны қолдану программаланған есептеулер схемасының жақсаруы және электорнды есептеу машиналарының құрылуымен айтарлықтай кеңейді. Қазіргі кезді сфералық тригонометрия ғылым мен техниканың көптеген тармақтарында қолданылуда. Олар: астрономияда, геодезияда, картографияда, географияда, теңізде жүзуде, авиация мен космонавтикада кеңінен қолданылуда.
Анықтамалар мен қажетті тұжырымдар.
Сфера - центрі деп аталатын нүктеден бірдей қашықтықта жататын кеңістіктегі нүктелердің геметриялық орнын білдіреді. Сфера ішіндегі кеңісттік бөлігі, шар фигурасын жасайды. Сфера центрі мен кез - келген шеткі бір нүктесін қосатын түзу кесінді - радиус, ал ценрі арқылы өтіп оның екі нүктесін қосатын түзу кесінді - сфераның диаметрі деп аталады.
1-сурет
Сфераның жазықтықпен кез - келген қимасы шеңбер болады. Сфераны К жазықтықпен қиғанда қандайда бір жабық қисық сызық пайда болады делік (1-сурет) . Сфераның О центрінен К жазықтыққа түсірілген перпендикуляр табанын С мен белгілеп, қию сызығынан жүргізілген екі D мен Е нүктелерін таңдап, оларды О, С нүктелерімен қосамыз. СD және СЕ сызықтары К жазықтығында жатқандықтан, СD
 ОС және СЕ
ОС және СЕ
 ОС болады. ОЕ мен ОD кесінділері тең, өйткені олар сфераның радиустары. Сондықтан ОСD және ОСЕ үшбұрыштары тікбұрышты және өзара тең. Бұл салудан келесі СD = СЕ екені келіп шығады, яғни D мен Е АDЕВ жабық қисықтың нүктелері К жазықтығын қиюшы С нүктеден бірдей қашықтықта жатады, демек қиюшы сызық С нүктеден бірдей қашықтықтағы геометриялық нүктелер орнын береді, яғни ценрі С нүктедегі шеңбер.
ОС болады. ОЕ мен ОD кесінділері тең, өйткені олар сфераның радиустары. Сондықтан ОСD және ОСЕ үшбұрыштары тікбұрышты және өзара тең. Бұл салудан келесі СD = СЕ екені келіп шығады, яғни D мен Е АDЕВ жабық қисықтың нүктелері К жазықтығын қиюшы С нүктеден бірдей қашықтықта жатады, демек қиюшы сызық С нүктеден бірдей қашықтықтағы геометриялық нүктелер орнын береді, яғни ценрі С нүктедегі шеңбер.
Егер R - сфераның радиусы, r - қима шеңбер радиусы және d - ОС перпедикулядың ұзындығы болса, онда әрбір өзара тең болған тікбұрышты үшбұрыштар үшін, мына теңдік орынды:
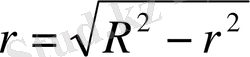 (1)
(1)
(1) - формула сфераның центрінен жазықтық қимасының d - арақашықтық өзгеруімен, қима шеңбердің r - радиусы да өзгереді. Сфераның О центрінен қима жазықтық К қаншама алыстаса қима шеңбердің радиусы сонша кішірейеді. Дербес жағдайда, d = R болса, қима шеңбер нүктеге, ал қима жазықтық сфераға жанама жазықтыққа айналады.
Қима жазықтық сфераның О центріне жақындай түссе, қима шеңбердің радиусы - r, сфераның R радиусына тең болады. Мұндай қию сфераны үлкен дөңгелек бойынша қию деп атлады. Берілген сфераның барлық үлкен шеңберлері, бір R радиусты шеңбер секілді, бір - біріне тең.
О центрі арқылы өтпейтін, қима жазықтығында жататын барлық шеңберлер - кіші дөңгелекті шеңберлер деп аталады. Егер қима жазықтықтар О центрден бірдей қашықтықта орналасқан болса, кіші дөңгелекті шеңберлер өзара тең болады. Жазықтықтары өзара параллель болған, қима дөңгелектер, мысалы РFР 1 G және АDЕВ, параллель дөңгелектер деп айтылады. Егер сфераның О центрінен АСВD жазықтығына, оның дөңгелегі болған бір үлкендөңгелегін перпендикуляр етіп қойсақ, онда ол шексіз екі жақа үлкею нәтижесінде Р және Р 1 диаметрлі қарама - қарсы екі нүктеде сфераны қияды және бұл нүктелер берілген үлкен дөңгелекті шеңбердің полюстері болады.
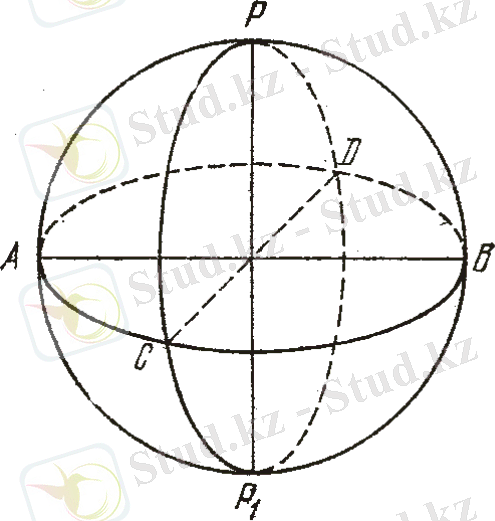
2- сурет
Р және Р
1
полюстері сфера диаметрінің екі жағында жататыны анық, сонымен қатар олар үлкен дңгелекті АСВD шеңбердің барлық нүктелерінен бідей бұрыштық арақашықтықта орналасып, олар полярлық немесе экватор деп аталады. Барлық үлкен дөңгелекті шеңбер доғалары РА, РС, РВ, РD, Р
1
А, Р
1
С, Р
1
В, Р
1
D және басқада төбесі сфераның О центрінде болған, әрбір тік бұрышпен тартып тұратындықтан, әрбір полялық нүктесімен полюстері арасындағы бұрыштық арақашықтығы
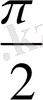 немесе 90° жасайды. Үлкен дөгелек АСВD шеңбері (2 - суретті қара) . Р және Р
1
екі полюстенде бірдей бұрыштық арақашықтықта тұрғандықтан, ол сфералық Р және Р
1
полюстері арқылы өтетін барлық үлкен дөңгелек шеңберлерін (медиандары) тең екіге бөледі. Бұдан келіп шығатыны, сфералық әрбір үлкен дөңгелекті шеңбері оны екі тең бөлікке бөледі. Сфераның Р, Р
1
полютерінен өтетін барлық үлкен дөңгелек шеңберлері РАР
1
В, РСР
1
D және басқалары, осы полюстердің АВСD экваторына перпендикуляр, өйткені олар үлкен дөңгелекті жазықтыққа салу бойынша перпендикуляр, РР
1
өсін өзіне қамтыған жазықтықтарда жатады. Керісінше егер қандайда бір үлкен дөңгелекке перпендикуляр болған бірқатар үлкен дөңгелектер салсақ, онда олардың барлығы осы үлкен дөңгелектің полюстерінен өтетін болады. СР
немесе 90° жасайды. Үлкен дөгелек АСВD шеңбері (2 - суретті қара) . Р және Р
1
екі полюстенде бірдей бұрыштық арақашықтықта тұрғандықтан, ол сфералық Р және Р
1
полюстері арқылы өтетін барлық үлкен дөңгелек шеңберлерін (медиандары) тең екіге бөледі. Бұдан келіп шығатыны, сфералық әрбір үлкен дөңгелекті шеңбері оны екі тең бөлікке бөледі. Сфераның Р, Р
1
полютерінен өтетін барлық үлкен дөңгелек шеңберлері РАР
1
В, РСР
1
D және басқалары, осы полюстердің АВСD экваторына перпендикуляр, өйткені олар үлкен дөңгелекті жазықтыққа салу бойынша перпендикуляр, РР
1
өсін өзіне қамтыған жазықтықтарда жатады. Керісінше егер қандайда бір үлкен дөңгелекке перпендикуляр болған бірқатар үлкен дөңгелектер салсақ, онда олардың барлығы осы үлкен дөңгелектің полюстерінен өтетін болады. СР
 АВ болғандықтан, СР доғасы АВ доғасына сфералық перпендикуляр болады.
АВ болғандықтан, СР доғасы АВ доғасына сфералық перпендикуляр болады.
Кеңістікте бір түзудің бойында жатпайтын үш нүктеден, жазықтық жүргізуге болады және тек біреу ғана. Серада жатқан А және D нүктерімен және оның О центрінен жазықтық жүргіземіз (3 - сурет) .
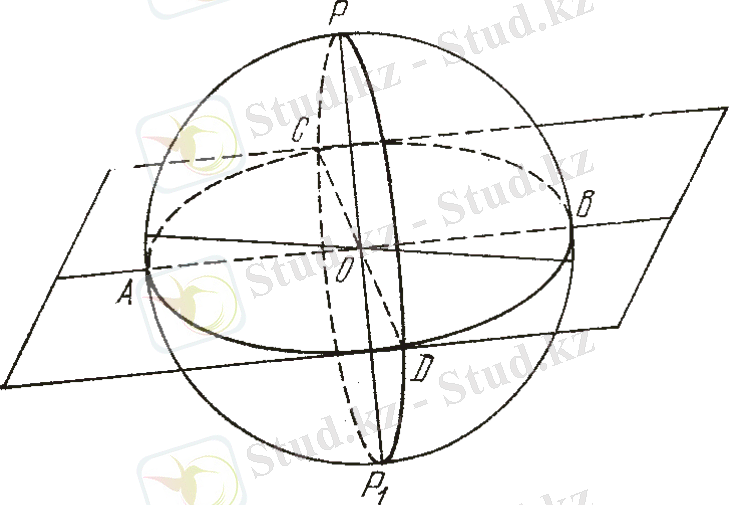
3 - сурет
Сераның центрінен өтетін әрбір жазықтық, онда үлкен дөңгелекті шеңбер жасап, сфераны қиып өтеді. Сондықтан, сферадағы АD үлкен дөңгелекті шеңбер доғасы болады. А, D және О нүктелері арқылы бір ғана жазықтық өтетін болғандықтан, сфераның А және D екі нүктелерінен тек бір ғана дөңгелекті шеңбер өтеді. Егерде осындай нүктелер сфераның бір диаметрінің екі шетінде болса (мысалы: А және В нүктерелі), онда А, В және О үш нүктеде де бір түзу бойында орналасады және олар арқылы шексіз көп жазықтықтар жүргізуге болады. Осылайша, жазықтықтың екі нүктесінен тек бір ғана түзу жүргізуге болатыны секілді, сферада да екі нүкте арқылы тек бір ғана үлкен дөңгелекті шеңбер доғасын салуға болады.
Геометрияда үлкен дөңгелекті шеңбер доғасы (180° - тан кіші) сфераның екі нүктесі арасындағы ең кіші арақашықтық екенін дәлелдейді.
Сферадағы ( АD доға бір бөлігі болатын) кіші дөңгелекті АDЕ шеңбері (4 - сурет) сфераның В сфералық центрі немесе полюсі деп аталатын нүктесінен бірдей арақашықтықтағы нүктелердің геометриялық орны болады. Сферадағы арақашықтық, яғни үлкен дөңгелекті шеңбердің АВ доғасы, В сфералық центрінен берілген кіші дөңгелекті шеңбердің кез - келген А нүктесіне дейінгі аравқашықтық сералық радиус
 делінеді.
делінеді.
Сфераны қиып өтетін, екі параллель жазықтық арасындағы сфера бөліге сфералық белдеу деп аталады. Егер де осы жазықтықтардың бірі сфераны қиып өтпей оған жанама жазықтық болса, онда параллнль жазықтықтар арасындағы сфера бөлігі сфералық сегмент болады.

4 - сурет
Сфералық тригонометрия өзінің шешуші пәні ретінде сфералық үшбұрышты қарастырады, ол шар бетінде үлкен дөңгелектердің қиылысуынан пайда болады.
Сфералық үшбұрыш жайлы түсінік.
Егер қандайда бір үш жақты - О нүкте төбесі, О
 , О
, О
 және О
және О

қабырғалары және де сол үш жақты бұрыштың төбесі сфераның центрі болатын бұрышты сферамен қиятын болсақ ( 5 - сурет), онда қимада сфералық үшбұрыш деп аталатын фигура сфера бетінде пайда болатын АВ, АС және ВС үлкен дңгелек доғалары пайда болады.
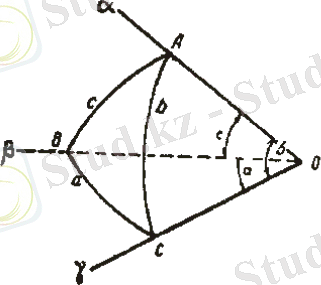
5- сурет
Керісінше, егер сферада үлкен дөңгелекті үш доғаның өзара қиылысуынан құрылған үшбұрышты фигура болса, онда ол фигураны сфера мен бұрышы сфера центрінде болған үш жақты бұрышпен қиылысу нәтижнсінде пайда болған фигура деп қарастыруға болады.
Егер де сферада үш нүкте А, В, С белгілеп, олардың екеуі арқылы үлкен дөңгелекті доға жасасақ, онда толығымен анық АВС үшбұрышы құрылады, өйткені сферадағы екі нүкте арқылы үлкен дөңгелектің тек қана бір доғасын салуға болады. Сондықтан сфералық үшбұрышты үлкен дөңгелектің екі доғасы мен үш қиылысулардан тұратын сфералық беттің бөлігі деп анықтауға болады.
Сфераық үшбұрыштың төбелері мен бұрыштарын латынның үлкен ( А, В, С ) әріптерімен, ал оларға қарсы жатқан қабырғаларды - сәйкесінше латынның кіші ( а, в, с) әріптерімен белгілейміз. Кез - келген сфералық үшбұрышта ұзындығы жартылай шеңберден ұзын болаған, яғни 180°- тан үлкен екі қабырғалы болуы мүмкін емес, өйткені әрбір 180°- тан үлкен болған екі қабырғадан сфералық үшбұрыш ешқашан салынбайды. Оның екі қабырғасы үшіншісімен кездеспейтін сферада сфералық екібұрыш деп аталатын фигура жасайды. Осылайша, сферадағы екі бұрыш деп, үлкен дөңгелекті жарты шеңберлердің қиылысуынан пайда болған фигураны айтады (6 - сурет) .

6- сурет
Егер сферадағы үшбұрыштың екі қабырғасы 180°-тан үлкен бола алмаса, онда бір үшінші қабырғасы ғана 180°-тан үлкен болуы мүмкін. Бірақ біз болашақта тек сферада берілген қос - қостан үш нүктені және үлкен дөңгелектің доғаларын ең кішісін қосудан пайда болған сфералық үшбұрышты қарастырамыз, яғни мұндай үшбұрыштардың барлық қабырғалары мен бұрыштары 180°- тан кіші. Мұндай сфералық үшбұрыштар эйлерлық үшбұрыштар деп аталады (атақты математик Леонард Эйлер, 1707-1783 ж. ж. ) .
Егерде қандайда бір қабырғасы 180°- тан үлкен сфералық үшбұрыш берілсе, онда оның орнына жарты сераға дейін қосылған басқа үшбұрышты қарастырамыз. Осы соңғы үшбұрыш эйлер үшбұрышы болады. Осы көмекші үшбұрыштың элементтерін біле отырып, берілген үшбұрышты да табуға болады.
Әртүрл екі үлкен дөңгелек бір димаетрдің ұштарындағы екі нүктеде қиылысатындықтан, біз білеміз, егер қандай да бір сфералық үшбұрыштың екі көрші қабырғаларын олардың екінші қиылысу нүктелеріне дейін жалпы бір диаметрде жатады.

7- сурет
Бұл салумен басқа бір сфералық, бастапқы АВС үшбұрышына қатынасы а қабырғасы бойынша түйіндес үшбұрыш болатын, үшбұрыш ВСА құрылады. Түйіндес А 1 ВС үшбұрыштың қабырғалары мен бұрыштары, негізгі үшбұрыш элементтері бойынша оңай табылады:
 А
1
=
А
1
=
 А а қабырғасы жалпы,
А а қабырғасы жалпы,
 ВСА
1
= 180° -
ВСА
1
= 180° -
 С, А
1
В = 180° - с қабырғасы
С, А
1
В = 180° - с қабырғасы
 А
1
ВС = 180° -
А
1
ВС = 180° -
 В, қабырғасы А
1
С = 180° - в
В, қабырғасы А
1
С = 180° - в
Сфералық үшбұрыш жақтарының арасындағы ара қатыс:
ОАВС үшқырлы үшбұрышта (5- сурет), сүйенетін оның жазық бұрыштары сфералық үшбұрыштың жақтарымен өлшенеді, ал екі қырлы бұрыштар сфералық үшбұрыштың сәйкес бұрыштарымен өлшенеді. Мұндай үшқырлы үшбұрыш пен оған сәйкес келетін сфералық үшбұрыш арасындағы тәуелділік үшқырлы бұрыш туралы теоремалар сфералық үшбұрышқада қолдануға болады.
1) Кез - келген үшқырлы бұрышта әрбір жазық бұрыш басқа екі жазық бұрыштың қосындысынан кіші болатындығы белгілі, яғни
АОС < АОВ + ВОС.
Бұл жазық бұрыштар сфералық үшбұрыштың жақтарымен өлшенетін болғандықтан,
 АОС = в,
АОС = в,
 АОВ = с,
АОВ = с,
 ВОС = а. Бұдан сфералық үшбұрыш үшін: в < а + с ие боламыз, яғни әрбір сфералық үшбұрыш жағы басқа екеуінің қосындысынан кіші болады.
ВОС = а. Бұдан сфералық үшбұрыш үшін: в < а + с ие боламыз, яғни әрбір сфералық үшбұрыш жағы басқа екеуінің қосындысынан кіші болады.
Теңсіздіктің бір мүшесін оң жақтан сол жағына аауыстыра отырып, осы теоремадан келіп шығатын бірінші салдарды аламыз:
в - с < а, яғни әрбір сфералық үшбұрыш жағы басқа екеуінің айырмасынан үлкен болады. а + с > в осы теңсіздіктің екі жағынада в - дан қоссақ, сонда а + в + с > 2в аламыз немесе соңғы теңсіздіктің екі жағын да 2 - ге бөлсек, онда теоремадан екінші салдарға ие боламыз:
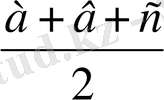 > в, яғни сфералық үшбұрыштың жарты периметрі әрқашанда оның әрбір жағынан үлкен болады.
> в, яғни сфералық үшбұрыштың жарты периметрі әрқашанда оның әрбір жағынан үлкен болады.
2) Кез - келген үшқырлы бұрышта оның жазық бұрыштарының қосындысы 360° - тан кіші болатыны белгілі:
 АОС +
АОС +
 ВОС +
ВОС +
 АОВ < 360°
АОВ < 360°
Жазық бұрыштарды оның өлшенетіндерімен сфералық үшбұрыштың жақтарымен алмастыра отырып: а + в + с < 360° аламыз, яғни сфералық үшбұрыш жақтарының қосындысы 360° - тан кіші болады.
 I - Тарау. Тікбұрышты сералық үшбұрыш.
I - Тарау. Тікбұрышты сералық үшбұрыш.
§ 1. 1. Сфералық тригоноетрияның негізгі формулалары.
Сфералық тригонометрияның негізгі формулалары бұл сфералық үшбұрыштың төрт немесе бес элементтерін байланыстыратын қатынастарды айтамыз, яғни берілген төрт немесе үш элементтері арқылы төртінші немесе бесінші элементтерін табуға мүмкіндік береді.
Косинустар формуласы:
Косинустар формуласы негізінен Альбатегния (Х- ғасырдың екінші жартысы) формулалары деген атпен белгілі.
Сфералық үшбұрыштың үш қабырғасын және бір бұрышын байланыстыратын формуланы айтамыз.
 Сфералық үшбұрыштың бір қабырғасының косинусы қалған екі қабырғаларының косинусының көбейтіндісіне, сол екі қабырғаның синусымен олардың арасындағы бұрыштың косинусының көбейтіндісіне қосқанға тең.
Сфералық үшбұрыштың бір қабырғасының косинусы қалған екі қабырғаларының косинусының көбейтіндісіне, сол екі қабырғаның синусымен олардың арасындағы бұрыштың косинусының көбейтіндісіне қосқанға тең.
а) Формуланың қорытындысы проекция теориясынан келіп шығады.
8-сурет
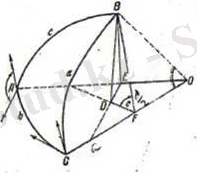
Айталық АВС - берілген сфералық үшбұрыш (8-сурет) . АВС үшбұрышының төбелерін сфераның О центрімен қосайық. В төбесінен үлкен дөңгелек жазықтығына перпендикуляр түсіреміз, үшбұрыштың қалған екі А және С төбелерінен өтетіндей және радиустарынада қосатын сфераның центрін сол төбелермен. Айталық ол перпендикулярлар ВD, ВЕ және ВF болсын. Осы перпендикулярлардың табандарын ЕD және FD түзулерімен қосқанда ОЕDF сынық тзулерін аламыз және ОD оның жанамасы болады. Алынған сынық түзулерді оське проекциялаймыз, оның бағытын жанама бағытымен бағыттас ете отырып.
Сонда мынадай қатынас аламыз:
пр. ОF = пр. ОЕ + пр. ЕD + пр. DЕ (1. 1)
Осы қатынасқа кіретін әрбір элементтің мәндерін қарастырып көрелік. ОF сызбадан көріп тұрғанымыздай соs
 - ға тең, О¯F -ті ОҒ - ке проекциялағанда да ол соs
- ға тең, О¯F -ті ОҒ - ке проекциялағанда да ол соs
 - ға тең болады, ал DF - тің проекциясы 0-ге тең, өйткені DF
- ға тең болады, ал DF - тің проекциясы 0-ге тең, өйткені DF
 ОF. Стереометриядағы «үш перпендикулярлар» теоремаға сүйене отырып ОF түзуінің АСО үлкен дөңгелектің жазықтығында жататынын айта аламыз және оған көлбеу жатқан ВF - ке перпендикуляр. Осы көлбеудің FD проекциясынада перпендикуляр болады.
ОF. Стереометриядағы «үш перпендикулярлар» теоремаға сүйене отырып ОF түзуінің АСО үлкен дөңгелектің жазықтығында жататынын айта аламыз және оған көлбеу жатқан ВF - ке перпендикуляр. Осы көлбеудің FD проекциясынада перпендикуляр болады.
ЕD проекциясын табу үшін, үш перпендикулярлар теоремасынан
DЕ
 ОЕ, бұдан
ОЕ, бұдан
 ВЕD екі жақты бұрыштың түзу бұрышы болады, ол
ВЕD екі жақты бұрыштың түзу бұрышы болады, ол
 А сфералық бұрышын өлшейтін ЕD арасындағы ЕKD бұрышын ескере отырып және оське проекциясы 90º - в болады, сонда мынаны аламыз
А сфералық бұрышын өлшейтін ЕD арасындағы ЕKD бұрышын ескере отырып және оське проекциясы 90º - в болады, сонда мынаны аламыз
пр. ЕD = ЕD соs(90º - в) = ЕD sinв;
ЕD = ВЕ соsА; ВЕ = sinс
Сондықтан
пр. ЕD = sinв sinс соsА
ЕО проекциясы . шін келесілерді аламыз:
пр. ЕО = ЕО соsв; пр. ЕО = соsс;
пр. ЕО = соsв соsс;
Ал енді алынған мәндерді (1. 1) өрнегіне қою арқылы мынаны аламыз:
соsа = соsв соsс + sinв sinс соsА (1. 2)
Дәл осылай қалған екі в және с қабырғалары үшін формуланы қорытып шығаруға болады, яғни
соsв = соsс соsа + sinс sinа соsВ
соsс = соsа соsв + sinа sinв соsС
Соңғы екі формуланы (1. 2) формуладан шеңбер бойымен әріптердің орнын ауыстырып қоя отырып, оңай түрде таба аламыз (9 - сурет)
9- сурет
Синустар формуласы:
Бұл формулар сфералық үшбұрыштың екі жағы ммен екі қарама-қарсы бұрыштары арасындағы тіуелділікті көрсетеді.
Сфералық үшбұрыш жақтарының синустары оларға қарама-қарсы жатқан бұрыштардың синустарына пропорционал.
а) Проекциялар туралы теоремалар негізінде формула қорытындысы келіп шығады.
BDE және BDF екі тікбұрышты үшбұрышын қарастырайық (8-сурет) . Олардың ортақ жақтарын екі сынық сызық ретінде қабылдап, осы сынық сызықтарды, тұйықтаушыға сәйкес келетін, проекция өсіне проекциялаймыз. Яғни:
пр. BD=пр. BE+пр. ED;
пр. BD=пр. BF+пр. FD;
бұдан
пр. BE+пр. ED=пр. BF+пр. FD
BD өсінен BE проекциясы BEcosDBE тең; BE, сызбара көрсетілгендей, sinC болады;
 DBE-(90˚-А) -ға тең, сондықтан
DBE-(90˚-А) -ға тең, сондықтан
пр. BE=sinc cos(90˚- А) =sinc sinA (1. 3)
BD өсінен ED проекциясы нөлге тең, себебі олардың арасындағы бұрыштың косинусы нөлге тең.
BD өсінен BF проекциясы BFcosFBE тең; BF=sina;
 FBE =90˚-C; сондықтан
FBE =90˚-C; сондықтан
пр. BF=sin a cos(90˚-С) = sin a sin C
BD өсінен DF проекциясы нөлге тең, себебі олардың арасындағы бұрыш 90˚-қа тең.
Алынған мәндерді (1. 3) теңдігіне қоя отырып, ие болатынымыз
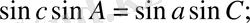
бұдан алатынымыз:
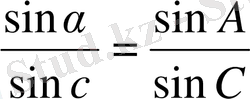 .
.
Дәл осылай

дәлелдеуге болады.
Кетірілген синустардың үш формуласынан біз тәуелсіз болаын тек екеуін ғана қабылдай аламыз, себебі үшінші қатынас олардың салдары болады. Осы барлық формулаларды келесі түрде жазуға болады:
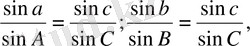
Бұдан
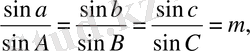 (1. 4)
(1. 4)
Яғни, сфералық үшбұрышта жағының синусы мен қарама-қарсы жатқан бұрыштың синусына қатынасы тұрақты шамаға тең.
б) Жағының негізгі косинустар формуласынан синустар формуласының қорытындысы
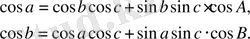
Бұл формулаларға және элементтері кіретінін көреміз, олардың арасындағы тәуелділікті табу керек, бірақ, бұл элементтерден басқа бізге қажет болмайтын с-да кіреді: Бұдан синустар формулаларының қорытынды есебі осы С элементін шығаруға алып келеді.
Әрбір теңдіктің оң жағының бірінші мүшесін сол жағына ауыстырып, әрқайсысының екі жағында квадраттайық.
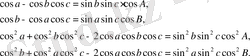
Бірінші теңдіктен екіншісін мүшелеп алып тастаймыз:

Ортақ көбейткіштерді жақшаның сыртына шығарсақ:
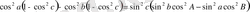
немесе
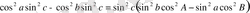
Теңдіктің екі жағында да
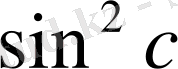 -ға қысқартамыз:
-ға қысқартамыз:
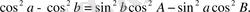
Осы теңдікте косинустарды синустармен алмастырайық:

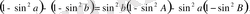

Қысқартудан кейін алатынымыз:
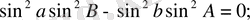
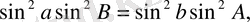
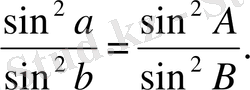
Теңдіктің екі жағынан да квадраттан құтыламыз.

- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz