Көрсеткіштік теңдеудің қолданылуы

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 23 бет
Таңдаулыға:

МАЗМҰНЫ

Кіріспе
3
1
Орта мектепте теңдеулерді оқыту әдістемесі
4
1.1
Теңдеулерді оқыту
4
1.2
Есеп шығару процесінің құрылымы
5
1.3
Теңдеулер мен теңсіздіктерді шешуде қажет болатын дағдылар
6
2
Көрсеткіштік функция және теңдеу ұғымы. Оны шешу жолдары
9
2.1
Көрсеткіштік функцияның анықтамысы
9
2.2
2.3
Көрсеткіштік теңдеудің қолданылуы
Көрсеткіштік теңдеу және оларды шешу әдістері
11
12
2.4
Көрсеткіштік және логарифмдік теңдеулерді түрлендіру
18
2.5
3
Көрсеткіштік теңсіздіктер
Практикалық сабақ жоспары
20
21
Қорытынды
Пайдаланылған әдебиеттердің тізімі
23

25

КІРІСПЕ
Қазіргі информациялау дәуірінде математиканың негізін меңгеру жас ұрпаққа білім беру мен тәрбиелеудің бірден-бір негізгі элементі болып табылады. Казіргі кезде дүние жүзіндегі көптеген елдерде математикадан мектептерде жүйелі де, сапалы білім беруге аса назар аударылып отырғаны белгілі. Бұл жөніндегі дүние жүзілік тәжірибеге талдау жасайтын болсақ , онда мынандай үш тенденцияны байқауға болады: барлық оқушыларға математикадан белгілі-бір дәрежеде білім берудің қажеттілігі және оған сәйкес ғылыми-зерттеу жұмыстарды кеңінен жүргізу. Математиканы негізгі курс ретінде жалпы білім беретін мектептердің сатысының оқу жоспарына енгізу: мектептің жоғарғы сатысында математикадан білім беруді жеке даралау мен топтау әдістері арқылы іске асыруды кеңінен енгізу. Математика оқушыларды индукция және дедукциямен, жалпылау мен нақтылаумен, анализ бен синтезбен, жіктеу және жүйеге келтірумен, абстракциялаумен аналогиямен таныстыра отырып, олардың ой өрісін едәуір кеңейтеді.
Математика курсының міндеті - оқушылардың логикалық ойлауын дамыту. Логикалық интуицияны дамытып, осының нәтижесінде математика мектеп оқушыларының ғылыми-техникалық ойлауын қалыптастыруда жетекші орын алады.
Математика оқытудың мақсаты-жеке тұлғаны қоғамның даму барысында алатын оның орнына лайық функцияналды сауаттылығын қалыптастыруға байланысты анықталады. Математиканы оқытудың білімділік мақсаты-барлық оқушыларды математика ғылымның негізі болатын білімдер жүйесі мен және ол білімдерді сапалы түрде қолдана алудың іскерліктері мен дағдыларын берік қалыптастыру болып табылады. Аталған білім-білік, дағдыны қалыптастыру математикалық жекелеген тараулары арқылы жүзеге асырылады. Сол тараулардың бірі-көрсеткіштік функция.
Зерттеу нысаны алгебра курсында көрсеткіштік функция тақырыбын оқытудың әдістемесі. Тарауды оқу барысында оқушылардың білім-білік дағдысына қойылатын талаптар:
-Көрсеткіштік функцияның қасиеттерін меңгеру және графигін сала алу.
-Көрсеткіштік теңдеулерді шешу әдістерін меңгеру.
Курстық жұмыстың мақсаты: оқушылардың көрсеткіштік теңдеулерді шешуіне бағытталған әдістемені құру.
Зерттеу кезеңдері:
-тақырыпты негіздеу, мақсаттары мен міндеттерін айқындау;
-тақырыпқа байланысты материалдар жинақтау, әдебиеттерге шолу жасау, талдау;
-көрсеткіштік теңдеулердің түрлерін қарастыру;
-алынған нәтижелер бойынша есептер жинағын құру, жинақтау.

1 Орта мектепте теңдеулерді оқыту әдістемесі
1.1 Теңдеулерді оқыту
Математиканы оқытуда есеп шығарудың үлкен маңызы бар. Оқушылардың математиканы оқып білудегі жетістігі олардың есепті шығаруға қаншалықты төселгендігіне қарай бағаланады.
Есеп шығару кезінде математикалық ұғымдардың көбінің мағынасы анық ашылып, нақтыланады. Мысалы, бастауыш класстарда жай мәтінді есептер арифметикалық амалдар мәнін ашу үшін пайдаланылады. Өйткені бұл класстарда ол амалдардың анықтамасы берілмейді. Амалдар мәні оқушыларға әр түрлі заттар жиыны мен практикалық операциялар негізінде түсіндіріледі. Оқушылар жай сюжетті есептер шығарғанда бұл операцияларды ақыл-ойдың іс-әрекеттеріне аударады.
Есеп шығарудың практикалық мәні зор: оқушыларды тұрмыста жиі кездесетін есеп - қисаптарды жасай алуға керекті біліммен қаруландырып, қажетті дағдыларды қалыптастырады. Сондықтан оларды келешекте өздігінен дұрыс шешім қабылдауға, жұмыс әдістерін тиімді пайдалануға, еңбек өнімділігін арттыратын әдіс- тәсілдерді іздеп табуға баулыйды.
Шығарылатын есептің рөлі мұғалімнің бұл есепті шығаруға ұсынғанда қандай мақсат қоюына байланысты. Кейбір жағдайларда оқып білуге тиісті теориялық материалдың мәнін, практикалық мағынасы мен маңыздылығын түсіну есептер шығару арқылы іске асырылады. Бұл жағдайда есептер шығару математикалық ұғымдарды қалыптастыруға мүмкіндік береді. Есептер шығару оқушылардың білімін толықтырып, нақтылау және дағдыларды қалыптастырып, одан әрі жетілдіру үшін пайдаланылады.
Ондай жағдайда есеп шығарудың мақсаты мынадай болады:
1) Есеп мазмұнына енетін шамалардың арасындағы себептілік пен салдарлық байланыстарды және функционалдық тәуелділіктерді тағайындау;
2) Есеп шығару тұжырымдауларын негіздей және логикалық дұрыс ойлай білуге үйрету;
3) Қолданылатын формулалар мен орындалатын амалдарды негіздеп дұрыс таңдай білу және әрі қарай қатесіз орындай алу;
4) Белгілі бір түрдегі есептерді шығару жолдарымен таныстыру.
Сонымен қатар есеп шығару кең көлемдегі тәрбиелік мақсатты да көздейді:
1) Көптеген есептер оқушылардың алған білімдерін оқу процесінде немесе өмірде, практикада қолдануға дайындайды;
2) Есеп шешуін іздеу оқушыларды қиыншылықты жеңуге жігерлендіреді, тапқырлыққа, зеректілікке тәрбиелейді;
3) Берілген есептің шешуін табудағы шығармашылық процеске қатысу оқушыға эстетикалық ләззат алуына жағдай жасап, эстетикалық тәрбие береді.

1.2 Есеп шығару процесінің құрылымы
Есеппен танысқаннан бастап оның толық шешімін алғанға дейінгі процесті қарастыратын болсақ, онда бұл процесс бірнеше кезеңнен тұратынын көреміз. Енді сол кезеңдерді анықтайық.
Есеппен танысқанннан кейін ең бірінші істелетін жұмыс, сол есептің шартымен танысып, оны элементар шарттарға ажырату, қандай талаптар қойылғанын анықтау, яғни есепке талдау жасау. Сонымен талдау жасау есеп шығару процесінің бірінші кезеңі болады.
Кей жағдайларда есепке жүргізілген талдауды қағазға түсіріп, жазуға тура келеді. Ол үшін есепті схемалық түрде жазулардың әр алуан формалары қолданылады. Есеп шығару процесінің екінші кезеңі, оны схемалық түрде жазу.
Есепті талдау мен оны схемалық түрде жазу, ол есепті шығару тәсілін іздеп табу үшін қажет. Бұл тәсілді іздеп табу - есеп шығару процесінің үшінші кезеңі болады.
Есеп шығару тәсілі табылғаннан кейін, оны іске асыру қажет. Ол есеп шығару процесінің төртінші кезеңі болады.
Есеп шығару процесі жүзеге асырылғаннан кейін, ол жазбаша не ауызша баяндалған соң, бұл шешудің дұрыстығын және оның есептің барлық шарттарын қанағаттандыратынын тексеру қажет. Ол үшін есеп шешуін тексереді, бұл есеп шығару процесінің бесінші кезеңі болады.
Көптеген есептерді шығарғанда, тексеруден басқа, ол есепке зерттеу жүргізуге, яғни қандай шарттар орындалғанда есептің шешімі болады және әрбір жеке жағдайда қанша шешімі бар немесе қандай жағдайда есептің тіпті шешімі болмайды т.с.с. қарастыруға тура келеді. Бұлардың барлығы есеп шығару процесінің алтыншы кезеңі болып, оны есепті зерттеу деп атайды.
Есеп шығарудың дұрыстығына көз жеткеннен кейін, қажет болған жағдайда оған зерттеу жүргізген соң, есептің шыққан жауабын анық етіп тұжырымдаған жөн. Бұл есеп шығару процесінің жетінші кезеңі болып табылады.
Ең соңында есепті шешу жолына талдау жасалады, яғни есеп шығарудың бұдан басқа тиімді тәсілі жоқ па, есепті шығару жолын жалпылауға болмай ма, шыққан шешімнен қандай қорытынды жасауға болады және т.с.с. Бұлардың барлығы есеп шығару процесінің ең соңғы, әрі қажетті сегізінші кезеңі болады.
Сонымен есеп шығару процесін сегіз кезеңге бөлуге болады:
1-ші кезең - есепті талдау;
2-ші кезең - есепті схемалық түрде жазу;
3-ші кезең - есепті шығару тәсілін іздестіру;
4-ші кезең - есеп шығаруды жүзеге асыру;
5-ші кезең - есеп шығарылуын тексеру;
6-шы кезең - есепті зерттеу;
7-ші кезең - есеп жауабын тұжырымдау;
8-ші кезең - есеп шығарылуына талдау жасау.

Есепті зерттеу. Есепте айтылған мағынадан шығып тұр, мұндағы х!=0, y!=0. Бұлар нольге тең болғанда есеп шартының мағынасы болмайтындықтан, біз есеп шығару процесінде х пен у нольге тең болмауы керек деп айқындап жазғанымыз жоқ.
Есеп шығару қорытындысында х=30, y=20 және x=20, y=30 түрінде екі жауап шықты. Шындығында бұл бір ғана жауап, себебі жұмысшының біреуі жұмысты 30 сағатта бітірсе, екіншісі 20 сағатта бітірген. Олардың қайсысын бірінші десек те, оның ешбір мағынасы өзгермейді.
Жауабы: жұмысшылардың біреуі(мүмкін біріншісі, мүмкін екіншісі) жұмысты 30 сағ, ал екіншісі 20 сағ бітіреді.
Есептің шығарылуына талдау жасау.Бұл есептің шығарылуы екі белгісізі бар екі теңдеулер системасы шешуге келтірілді.
Жұмыс көлемін бір өлшем деп алдық, оны z әрпімен белгілесек,онда системаның екінші теңдеуінің алымында болады да қысқарып кетеді.

1.3 Теңдеулер мен теңсіздіктерді шешуде қажет болатын дағдылар
Әдістемелік әдебиетте дағды деген сөз тіркесі бар. Мысалы, А.В.Петровский дағды дегенді нақты бір теориялық немесе практикалық тапсырмаларды шешу үшін өзінің қабілеттерін, білімін және түсінігін қолдана алу деп түсінеді. Т.Б.Булыгинаның ойынша дағды - ол белгілі бір істі саналы түрде жасау. М.В.Матюхина келесі түрде анықтама береді: Дағды - бұл қызметті табысты түрде орындауды қамтамасыз ететін білім мен қабілеттердің ұйқастылығы. Дағдылар - бұл істерді орындаудағы роботтандырылған әдіс. Білім - бұл түсініктегі түрлердің субъектіліктүрлілігі. Түсінік - бұл бір оқшауланғандықты және ерекшеліктікөрсететін,бір уақытта және барлығын қосып алғандағы білім түрі.
Келесі түсініктерді қарастырайық: Дағдыларды қалыптастыру. Ол мұғалімнің оқушыларды оқытқан сәтте белгілі бір әлеуметтік тәжірибені алуын білдіреді. Дағдыларды қалыптастыру - бұл пәннен алынатын білімде бар ақпараттарды анықтау және қайта қарастыру бойынша барлық қиын жүйелерді меңгеру. Дағдыларды қалыптастыру бұл негізінде білімді тереңдету түрінде қолданылады. Дағды зерттелетін белгілі бір заттар туралы түсініктерді меңгеру негізінде қалыптасады. Дағдыларды қалыптастырудағы негізгі жол - бұл оқушыларды заттардың барлық жақтарын көруге, оларға әртүрлі түсініктер беру, сол затқа әртүрлі көзбен қарауды үйрету. Затты талдау арқылы синтездің көмегімен түрлендіруді оқушыларға үйрету. Қолданылатын түрлендіру қандай қарым-қатынас және тәуелділік талап етілуіне байланысты. Осындай түрлендірулер тапсырмаларды шешу жоспары болып саналады. Дағдыларға үйрету әртүрлі жолдар арқылы жүзеге асыруға болады. Оның бірі оқушыларға қажетті білімді беріп, содан соң оларға орындау үшін тапсырмалар береді. Содан соң оқушы сол тапсырманы шешу үшін мүмкіндіктер мен қателерді қолдану арқылы сәйкес бағдарларды, ақпараттарды қарастыру және қызметте қодану арқылы шешім іздейді. Бұл жолды мәселелі оқыту деп атайды. Келесі жол, ол тапсырманы шешу үшін оның түрін және талаптарын жедел анықтау бойынша белгілерге үйретеді.
Бұл жолды алгоритмделген оқыту немесе толық бағдарланған негіздегі оқыту деп атайды. Соңында, бұл жол ол оқушының білімін қолдану үшін психикалық қызметке үйрету болып табылады.Бұл жағдайда мұғалім оқушыны тек қана белгілер мен тапсырмаларды айыра алу бағдарларына ғана үйретіп қоймай, сонымен қатар алға қойылған тапсырмаларды шешу үшін алынған ақпараттарды қолдануды ұйымдастырады. Бірінші кезеңде заттың бұл бағдарлары (маңызды ерекшеліктер) оқушыға дайын, заттты түрде, сызба түрінде, символ, зат түрінде, ал бағдарларды анықтау бойынша шаралар заттай іс-әрекеттер түрінде қолданылады. Бағдарлар мен заттай бағдарлар екінші кезеңде қалады, оларды ойлау шаралары, сөйлеу және жасау түрлерімен алмасады. Үшінші кезеңде сөйлесу әрекеттері де түсіп қалып, оларды ойлау шаралары алмастырады, ол барлық сызба бойынша таралады.
Бұл кезеңді ойлау қабілеттерін қалыптастыру әдісі деп атайды. Бірақ қарапайым түрде оқытуда бұл кезеңдер саналы түрде ұйымдастырылады. Сондықтан оқушы өзі қажет белгілерді анықтап, ал бастысы - осы әрекетті өзі таңдау керек. Қателіктерге көп жол беріледі. Түсініктер әрқашан толық әрі дұрыс болмайды.Дәстүрлік оқыту, дербес ойлану мен нәтижелері арқылы түзетуге негізделгендіктен, оқушының дұрыс түсінбеуіне алып келеді. Сонымен қатар оқушының қызметі ұғымдарды құруға, олардың белгілерін іздеуге қосарланбауы керек, соған қоса, түсініктерді мағына берумен толықтыру үшін, оның қолдану тәсілдерін меңгеру керек - бұл қызмет жалғыз өзі ғана маңызды заттарды белгілері бойынша іздеу емес, ал осы белгілерді қолдану. Түсінік толық әрі қатесіз құрылу үшін, оқушының сәйкес жұмысы толық бағдарлы негізде құрылуы тиіс. Олай болмаса, мұғалім оқушыларға заттардың барлық дайын белгілерін беруі керек, сонымен қатар әрбірін анықтау мен қолдану үшін қажетті шараларға баланы оқыту қажет.
Есепті теңдеу арқылы шығарудың рөлін ұғыну үшін, ең алдымен бұл тәсілдің мәнісі неде соны қарастырамыз. Мына есепті теңдеу құру арқылы шешу керек болсын: 28 ер адам және бірнеше әйелдер экскурсияға шықты. Олардың барлығы 25 адамнан сиятын екі автобусқа отырды. Экскурсияға қанша әйел шыққан?.
Экскурсияға шыққан әйелдер санын қандай да бір әріппен, мысалы х әрпімен белгілейміз.
Теңдікті құру үшін түрлі байланыстарды атап көрсетуге болады, бұл байланыстарға сәйкес өрнектер құруға және оларды теңестіру арқылы мынадай теңдеу алуға болады:
а) Есептің шартында барлық ерлер мен әйелдер автобуспен кеткендігі айтылған, демек, экскурсияға қанша ерлер және әйелдер кеткендігін (28 + х) өрнегімен және қанша ерлер мен әйелдер автобусқа отырғандығын (25*2) өрнегімен өрнектеуге, содан кейін бұл өрнектерді теңестіруге болады; сонда 28+х=25x2 теңдеуі шығады; бұл теңдеуді шешіп, есептің сұрағына жауап аламыз.
б) Есептің шартында әр автобусқа 25 адамнан отырғандығы айтылған, демек, әр автобустағы адамдардың санын басқа сандар арқылы өрнектеп, алынған өрнекті 25 санына теңестіруге болады, сонда (28+х):2=25 теңдеуі алынады. Осылайша пайымдау арқылы, басқа да теңдеулерді құруға болады.
Сонымен теңдеулер құру арқылы есептер шығару үшін белгісіз санды (ізделінді немесе басқа белгісіз санды) әріппен белгілейді, есептің шартында, құрамында белгісіз шама бар, теңдікті (теңдеуді) құруға мүмкіндік беретін, байланыстарды бөліп көрсетеді. Алынған теңдеуді шешеді. Мұнда алынған теңдеудің шешімі есептің мазмұнымен байланыстырылмайды.
Кез келген есептің шешуін көрсетілген жоспарды басшылыққа ала отырып, теңдеу құру арқылы орындауға болады. Бұл есептерді теңдеулер құру арқылы шығару тәсілінің жан-жақтылығын көрсетеді және оның артықшылығын анықтайды. Сонымен қатар, есептер теңдеулер құру тәсілімен шығару теңдеулер ұғымын игеруге көмектесетіндерін көріп отырмыз.

2 Көрсеткіштік функция және теңдеу ұғымы. Оны шешу жолдары
2.1 Көрсеткіштік функцияның анықтамысы
Анықтама. Егер а0, a!=1 болса,онда y=ax функциясын негізі a-ға тең көрсеткіштік функция деп атайды.
Мысалы, y=3x; y=10x ; y=0,2x y=12x y=2 ͯ және т.с.с. көрсеткіштік функциялар болады. Анықтамадағы a0, a!=1 шарттары өте маңызды. Мәселен, нақты көрсеткішті дәрежелер тек оң сандар үшін анықталғандықтан, a0 болуы қажет. Екінші жағынан, егер a=1 болса, онда әрбір x∈ (-infinity; +infinity) мәнінде
y=ax=1x=1 болып, функция x-ке тәуелді болмай қалады (бұл жағдайда кейде функцияны тұрақты функция y=1 ретінде қарастырады).
Көрсеткіштік функцияның қасиеттері.
Сонымен, енді көрсеткіштік y=ax функциясы a0 және a!=1 болғанда анықталған деп есептейміз.
Көрсеткіштік функцияның мынадай қасиеттері бар.
1∘. Көрсеткіштік функцияның анықталу облысы (-infinity;+infinity) жиыны болады.
2∘. (0;+infinity) жиыны көрсеткіштік функцияның мәндерінің облысы болады, яғни , ax0, x∈ (-infinity; +infinity) теңсіздігі орындалады.
3∘. а) Егер a1 және x0 болса, онда ax1 болады;
ә) егер a1 және x0 болса, онда ax1 болады;
б) егер a1 және x0 болса, онда ax1 болады;
в) егер a1 және x0 болса, онда ax1 болады;
г) егер a0 және x=0 болса, онда a0=1 болады;
4∘. Егер a1 болса, онда y=ax көрсеткіштік функциясы өспелі болады, яғни x1x2 теңсіздігін қанағаттандыратын әрбір x1, x2 нақты сандары үшін a ͯ1a ͯ2теңсіздігі орындалады.
5∘. Егер 0a1 болса, онда y=ax көрсеткіштік функциясы кемімелі болады, яғни x1x2 теңсіздігін қанағаттандыратын әрбір x1, x2 нақты сандары үшінa ͯ1a ͯ2 теңсіздігі орындалады.
Дәлелдеу: 1. Бұл қасиеттің дәлелдеуі анықтамадан шығады.
2. Оң санның рационал көрсеткішті дәрежесі оң болатынын білеміз, яғни x рационал сан болғанда ax0 теңсіздігі орындалады. Онда ax0 теңсіздігі кез келген иррационал x үшін орындалады. (1∘-қасиет)
3. а) Егер a1 және x0 болса, онда нақты көрсеткішті дәреженің 2∘-қасиеті бойынша ax1x=1.
ә) Егер a1 және x0 болса, онда ax1x=1.
б) және в) пункттері де осы сияқты дәлелденеді. Ал г) пунктінің дәлелдеуі көрсеткіші 0-ге тең дәреже анықтамасынан шығады.
4. a1 және x1x2 болсын. Онда ax2-ax1=ax1ax2-x1-10,себебі x2-x10 болғандықтан, ax2-x1-10. Олай болса, теңсіздіктің анықтамасы бойынша ax2ax1.
5. 0a1 және x1x2 болсын. Онда ax2-ax1=ax1ax2-x1-10, себебі, ax10, ал x2-x10 және 0a1 болғандықтын, ax2-x11.

Көрсеткіштік функцияның графигі.
Алдымен кестелер көмегімен y=2x және y=12xфункцияларының графиктерін салып көрейік:
x
-3
-2
-1
0
1
2
3
2x
18
14
12
1
2
4
8
12x
8
4
2
1
12
14
18
Табылған нүктелерді координаталық жазықтықта бейнелеп, оларды біркелкі тегіс сызықтармен қосамыз. Сонда y=2x (33-сурет) және y=12x (34-сурет) функцияларының графиктерін аламыз.

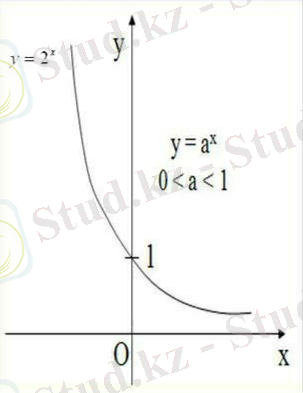
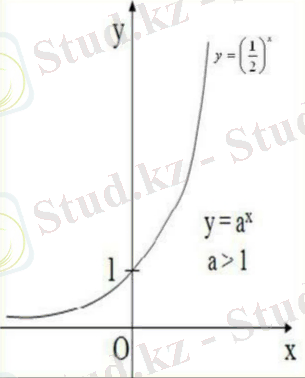
(33-сурет) (34-сурет)
Дәреженің қасиеті бойынша 1ab жағдайында, егер x0 болса, онда axbx теңсіздігі; егер x0 болса, онда axbx теңсіздігі орындалады. Ал керісінше 0ab1 жағдайында, егер x0 болса, онда axbx теңсіздігі; егер x0 болса, онда axbx теңсіздігі орындалады. Олай болса, негізі a 1-ден неғұрлым үлкен болса, онда сәйкес y=ax көрсеткіштік функциясы соғұрлым жылдамырақ өседі. Ал негізі a 1-ден неғұрлым кіші болған сайын сәйкес y=ax көрсеткіштік функциясы соғұрлым жылдамырақ кемиді. Мысалы, 35-суретте a=0,8; a=0,4; a=3; a=2 болғандағы сәйкес көрсеткіштік функциялар графиктері салынған.

2.2 Көрсеткіштік теңдеудің қолданылуы
Есептеу тәсілдерін жетілдіру XVII ғасырдың өзекті мәселелерінің бірі болып табылды. Сол кездердегі сауда жасау географиясын одан әрі кеңейту үшін Англия, Франция, Голландия сияқты мемлекеттерге қарапайым есептеулер жүргізетін инженерлер мен арифметиктерге деген үлкен сұраныс болды. Көрсеткіштік функция мен логарифмді ойлап табу - есептеу техникасының үлкен жетістігі болып саналды.
Көрсеткіштік функция ұғымы XVII ғасырдың соңында пайда болды. Осы көрсеткіштік функция бағытында үлкен жетістіктерге қол жеткізген және осы ұғымды алғаш енгізген шотландық ғалым Джон Непер.
Анықтама. y=ax түрінде берілген теңдеу көрсеткіштік функция деп аталады. Мұндағы a-саны негіз деп аталады, ол әр уақытта a0, яғни оң сан және a!=0 болуы шарт.
Енді кезекте көрсеткіштік функцияның қасиетіне тоқталып өтейік:
1) Функцияның анықталу облысы барлық нақты сандар жиыны, яғни 2) Функцияның мәндерінің облысы барлық оң нақты сандар жиыны, яғни . (0;+infinity)
3) Егер a 1 болса, онда y=ax функциясы барлық нақты сандар жиынында өседі, яғни бірсарынды өспелі.
4) Егер 0 a 1 болса, онда y=ax функциясы барлық нақты сандар жиынында кемиді, яғни бірсарынды кемімелі.
Осы көрсеткіштік функция мен оның қасиеттерін пайдалана отырып көрсеткіштік теңдеу ұғымына тоқталайық.

Көрсеткіштік функция графигі
2.3 Көрсеткіштік теңдеу және оларды шешу әдістері
Белгісіз шама дәреженің көрсеткішінде болып келетін теңдеулерді көрсеткіштік теңдеулер деп атайды.
Көрсеткіштік теңдеулер;
- бірдей негізге келтіру;
- жаңа айнымалы енгізу;
- графиктік;
- логарифмдеу тәсілдерімен шешіледі.
Бірдей негізге келтіру арқылы шығарылатын теңдеу.
1) ax=b ( a0, a!=1)
Егер b0 болса, теңдеудің жалғыз ғана түбірі бар болады.
Егер b=0 болса, теңдеудің түбірі жоқ болады.
2) af(x)=ag(x) мұндағы (a0, a!=1) теңдеуінің сол және оң бөліктерінің негіздері бірдей болғандықтан, af(x)=ag(x) теңдеуі f(x)=g(x) теңдеуімен мәндес болады.
Мысал: 5x=125
Шешуі: 1250, 125=53 ,5x=53, x=3 Жауабы: 3
Мысал: 2x-1=1
Шешуі: 2x-1=20, x-1=0, x=1 Жауабы:1
Мысал: 0,2x-0,55= 5∙0,04x-1
Шешуі: барлық дәрежелерді бір ғана 5негізге келтіреміз.
Сонда 50,5-x ∙5-0,5=5∙5-2x+2 теңдеуін аламыз, оны 5-x=5-2x+3 түріне түрлендіреміз де, дәреже көрсеткіштерін теңестіріп,теңдеуді шешеміз:
- x= -2x+3, x=3 Жауабы: 3
Жаңа айнымалы енгізу арқылы жиі шығарылатын теңдеулер.
1) A∙a2x+B∙ax+C=0 a0, a!=1
ax=y, y0 деп белгілесек, у-ке қатысты квадрат теңдеуге келеді. Ay2+By+C=0
Мысал: 52x-6∙5x+5=0
Шешуі: 5x=y, y0 белгілесек у-ке байланысты y2-6y+5=0 квадрат теңдеуіне келеміз. Бұдан y1=1, y2=5 екенін табамыз.
у-тің екі мәніне сәйкес екі көрсеткіштік теңдеу шығады.
1) 5x=1, x=0 5x=5, x=1
Бұл теңдеулерден есептің екі жауабы шығады. Жауабы: 0; 1
2) A∙ax+B∙a-x+C=0 ax=y (y0) деп белгілесек,
Ay2+Cy+B=0 квадрат теңдеуге келеміз.
Мысал: 5x-24=25∙5-x
Шешуі: 5x=y, y2-24y-25=0 квадрат теңдеуге келеміз.
y0
y1= -1; y2=25 у - тің таңбасын ескере отырып теңдеуді шешсек, 5x= -1 (бұл теңдеудің нақты түбірі жоқ),өйткені кез келген хEuroR үшін 5x05x=25, 5x=52, ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.