Жазық турбуленттік ағыншаның бастапқы бөлігін есептеу

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 47 бет
Таңдаулыға:

Қазақстан республикасы білім және ғылым министрлігі
Қазақ мемлекеттік қыздар педагогикалық университеті
Физика кафедрасы

Қорғауға жіберілді
“____”___________2010 ж.
Кафедра меңгерушісі
ф.-м.ғ.д., проф.
_________________ А.Қ.Ершина

дипломдық жұмыс

Тақырыбы: Екі бүйірі жағынан қабырғамен шектелген жазық турбуленттік
ағыншадағы кезектесуді зерттеу

050110-Физика мамандығы бойынша
(сырттай бөлім 5 жылдық 5 курс)

Орындаған: ___________________________ З.Р. Розахунова

Ғылыми жетекші,
аға оқытушы _________________________ А.С.Көпенбаева

Алматы, 2010 ж.
Мазмұны

Реферат ... ... ... ... ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ...
... ... .3

Шартты белгілеулер
тізімі ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... 4

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... . ... ... ... ... 5

I Жазық турбуленттік ағыншаның аэродинамикасын зерттеуге қысқаша
мағлұмат ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... . ... ... ... ... ... 7
1. Жазық турбуленттік ағыншаның негізгі заңдылықтары
... ... ... ... ... ... ... ..7
2. Үшөлшемді турбуленттік ағыншаның аэродинамикасының эксперименттік
зерттелуі ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ...
... ... ... ... ... 9
1.3 Жазық турбуленттік ағыншаның бастапқы бөлігін есептеу ... ... ... ... ... ..11
1.4 Жазық турбуленттік ағыншаның негізгі бөлігін есептеу
... ... ... ... ... ... ... .15
1.5 Жазық еркін ағыншаны эксперименттік зерттеу ... ... ... ... ... ... ... ... ... 18
1.6 Жазық турбуленттік ағыншаның жылдамдығының өзгерісіне екі бүйірінен
шектеуші қабырғалардың әсерін
зерттеу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .19

Зерттеу мақсатының
қойылуы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...25

2 Турбуленттілікті және жазық турбуленттік ағыншаның дамуына шектеуші
қабырғалардың әсерін эксперименттік
зерттеу ... ... ... ... ... ... ... ... ... ... ... ... ... ..26
2.1 Эксперименттік қондырғы және өлшеу әдістемесі
... ... ... ... ... ... ... ... ... ..2 6
2.2 Жақын орналасқан екі бүйірінен шектеуші пластиналардың арасында
таралатын жазық ағыншаның жылдамдығының профилін өлшеу нәтижелері...35
2.3 Жазық ағыншаның бастапқы бөлігіндегі ірі масштабты құйындардың дамуын
зерттеу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ..38
2.4 Орташа жылдамдық пен температураның профильдерінің z осі бойынша өлшеу
нәтижелері ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... .41
2.5 Ағыншаның турбуленттік сипаттамаларын өлшеу
нәтижелері ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ... ... .46
Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ... ...58
Қолданылған әдебиеттер
тізімі ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ..59
Реферат

Дипломдық жұмыс - 60 беттен, 23 суреттен және 12 қолданылған
әдебиеттен тұрады.
Қайнар сөздер: СОПЛО, жазық еркін ағынша, шектеуші пластинкалар, ірі
өлшемді құйындар, араласу жолы, турбуленттілік, жылдамдық таралуы.
Дипломдық жұмыстың I бөлімінде турбуленттілік ағыншаның таралу
заңдылықтары жайлы қысқаша мағлұмат, турбуленттік ағыншаның бастапқы және
негізгі бөліктері үшін жазық есептеулер, сонымен қатар жазық турбуленттік
ағыншаның таралуына шектеуші пластиналардың әсерін есептеулері келтірілген.
Жұмыстың екінші бөлімінде эксперименттік қондырғы, өлшеу әдістері, өлшеу
нәтижелері және оларды талқылау келтірілген.
Эксперимент нәтижелері теориялық есептермен салыстырылған.

Шартты белгілеулер тізімі

х,у,z –тік бұрышты декарттық координаталар;
2b – сопланың ені, м;
2h – екі бүйірінен шектеуші пластиналардың ара қашықтығы, м;
( – ағыншаның шартты қалыңдығы, м;
u – жылдамдықтың х осіне проекциясы, мс;
v - жылдамдықтың у осіне проекциясы, мс;
um – ағыншаның осіндегі жылдамдық; мс; (максималь жылдамдық)
( – динамикалық тұтқырлық коэффициенті, кгмс
( – кинематикалық тұтқырлық коэффициенті, м2с
( - тығыздық, кгм3
( – үйкеліс кернеуі, Нм2
( - кедергі коэффициенті
d – гидраврикалық диаметр, м
uо- ағыстың бастапқы жылдамдығы, мс;
- Рейнольдс саны;
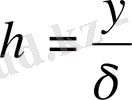- өлшемсіз координата;
к – ағыншаның толық импульсі;
hb – ағыншаның қабырғаларының қатынасы;
( - тоқ функциясы

Индекстер:
о – сопланың ернеуіндегі бастапқы шарт
m – ағыншаның осіндегі шарт
Кіріспе

Ағыншалық ағысты зерттеу барысында негізінен осесимметриялы және жазық
параллель ағыншалар қарастырылады. Эксперименттік зерттеулер жүргізгенде
кеңістіктік турбуленттік ағыншаны зерттеу көбінесе ескерілмей қалып қойды.
Соңғы жылдары техниканың көптеген түрлерінде, мысалы, реактивті
двигательдің жану камерасында, ұшақ қанатының шекаралық қабатын басқаруда
шыны өндірісінде, химиялық технологияда және т.б. ағыншалық ағыстың кеңімен
қолданылуына байланысты еркін және қабырғалық турбуленттік ағыншаны
зерттеуге көптеген теориялық және экспериментальдық зерттеулер жасалынған.
Мұндай зерттеулердің негізгі нәтижелері Г.Н. Абрамович [1], Бай Ши-и
[2], Л.А. Вулис, В.П. Кашкаров [3], А.С. Гиневский және т.б. ғалымдардың
монографияларында келтірілген.
Соңғы жылдары еркін және қабырғалық ағыншаның тік ағыншаға өтуін және
ірі масштабты дискретті құйындардың пайда болуын, оның таралып дамуын оқып
үйренуге ерекше көңіл бөлуде.
Жазық турбуленттік ағыншаны зерттеу үшін қашанда шыға беріс қимасы тік
бұрышты (биіктігі 2h ені 2в) сопладан шығатын ағыншаны қарастыруға тура
келеді. Жазық ағыншаны зерттеу үшін соплоның шыға беріс қимасының
қабырғаларының қатынасы 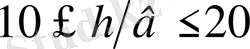аралығында алынады және саңлау екі бүйірінен
бір бірінен 2h қашықтықта жазық пластиналармен шектеледі. Осы кезде егер
шектеуші қабырғалардағы шекаралық қабаттың қалыңдығы h-тан аз болса,
ағыншаны биіктігі шексіз соплодан шыққан деп есептейді.
Бірақ [7,8,9] жұмыстарда көрсетілгендей биіктігі шектеулі соплодан
шыққан жазық ағыншаның таралуында ағыншаның бастапқы бөлігінде пайда болған
ірі масштабты құйындар едәуір әсер етеді, осының нәтижесінде соплодан аз
ғана қашықтықта ағыс үш өлшемді болып кетеді және 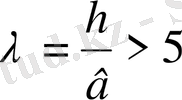, (2h соплоның
биіктігі, 2в - ені) болғанда саңлаудың биіктігіне параллель осі
бойынша жылдамдық профилінде бірнеше максимумдар мен минимумдар пайда
болады. Соплодан қашықтаған сайын жазық еркін ағыншаның жылдамдық
профилінде болатын мұндай біртексіздіктер әлі толық зерттелмеген.
Ағыстың құйындық құрылымының визуальды картинасын көлеңкелік әдіспен
зерттеу арқылы ірі масштабты құйындарды көруге және олардың дамуын
ағыншаның тек бастапқы бөлігінде ғана көруге болады. Ағыншаның аралық және
негізгі бөліктерінде құйындық құрылымды визуальды бақылау мүмкін емес.

Сондықтан дипломдық жұмыстың мақсаты жазық турбуленттік ағыншаның
бастапқы және аралық бөліктерінде пайда болатын ірі масштабты құйындардың
дамуын және олардың екі бүйірінен жазық пластиналарымен шектелген ағыншаның
таралуына әсерін зерттеу болын табылады. Бұл кезде соплоның нақты
геометриялық өлшемдері алынады.
Сонымен қатар дипломдық жұмыстың мақсаты құйындық құрылымды жылдамдық
пульсациясының жиілік спектрін, соплоның әр түрлі өлшемдері үшін ағыншаның
қималарында турбуленттік ағыншада болатын кезектесуді және Рейнольдс
санының мәнін термоанемометрлік құралдың көмегімен зерттеу болып табылады.

I Жазық турбуленттік ағыншаның аэродинамикасын зерттеуге қысқаша мағлұмат
1.1 Жазық турбуленттік ағыншаның негізгі заңдылықтары

Турбуленттік ағыншаның көп зерттелген түрі – тынышталған ортада
таралатын ағынша; ондай ағынша батырылған ағынша деп аталады. Батырылған
ағынша радиусы R дөңгелек соплодан (осесимметриялы ағынша) немесе ені 2в
және ұзындығы 2h тік бұрышты саңлаудан (жазық ағынша) шығады. Батырылған
ағыншаның схемасы 1-суретте келтірілген.

1-сурет. Жазық батырылған ағыншаның схемасы

Жылдамдық өрісі біртекті болғанда батырылған ағыншаның бастапқы
бөлігінде оның шекаралық қабаты таралған болады да, соплоның ернеуінде
қиылысады. Ағыншаның сыртқы қабаты қозғалыссыз сұйықпен шектеледі. Сыртқы
қабаты дегеніміздің өзі 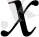осі бойынша жылдамдық құраушылары нөлге тең
бет. 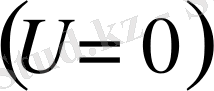шекаралық қабат ішкі жағынан жылдамдығы тұрақты ядроға өтеді.
Сондықтан шекаралық қабаттың ішкі жағында ағын жылдамдығы бастапқы
жылдамдыққа тең . Тікбұрышты соплодан ағып өтетін батырылған
үшөлшемді турбуленттік ағынша келесі ерекшеліктерге ие.
Біріншіден, егер осьтік жылдамдықтың азаю заңын қарастырсақ,
мұндай ағындарда үш облыстың бары байқалады.
1) Бастапқы бөлік немесе осьтік жылдамдықтың тұрақты облысы
(Um~const). Бұл бөлік ағынның өту жылдамдығына жақын және
ішкі шекаралар арасындағы қосылу қабаттарынан ось бойындағы
тұрақты жылдамдықтың потенциалды ядросының барымен мінезделеді.
Потенциалдық ядрода ағынша жылдамдығы тұрақты болады және оның
бастапқы жылдамдығына тең болады. Соплодан қашықтаған сайын ағынша
жылдамдығы азая береді
2) Өткінші бөлік. Бұл жерде өтудің бастапқы шарттары осьтік
жылдамдықтың құлау заңдылықтарына қатты әсерін тигізеді. Сопло
қабырғалары қатынастары параметрінің жеткілікті үлкен мәндерінде
жазық ағынның осьтік жылдамдығының азаю заңына әділ,
сондықтан бұл - өткінші бөлік деп аталады (Um~х-0,5). Бұл жерде
өтудің бастапқы шарттары осьтік жылдамдықтың құлау
заңдылықтарына қатты әсерін тигізеді. Сопло қабырғалары
қатынастары параметрінің жеткілікті үлкен мәндерінде жазық
ағынның осьтік жылдамдығының азаю заңына әділ, сондықтан бұл -
өткінші бөлік деп аталады (Um~х-0,5).
3) Осьтік симметриялы негізгі бөлік. Бұл облыста осьтік
жылдамдықтың өзгеруі осьтік симметриялы ағысқа сәйкес келетін
(Um~х-1) заңына бағынады. Ағыс тұтастай осьтік симметрияға
жақын және өтудің бастапқы шарттарынан тәуелсіз. Ағыспен төмен
қашықтықта осьтік симметрилы ағыстың енген төртінші облысы
орналасқан. Бұл бөліктегі жылдамдық профилі афинды ұқсас болып
келеді. Координаталардағы өлшемсіз жылдамдық профилі әмбебап
болады. Мұндағы -ағынша осіндей максималь жылдамдық, -
ағыншаның шартты қалыңдығы, ол нүктеден оське дейінгі қашықтыққа тең,
.
Екіншіден. Шығу қимасы тіктөртбұрышты пішінді сопладан өтетін
үшөлшемді ағынның дамуы оның көлденең қимасының деформациясымен
бірге жүреді, яғни тікбұрыштың қысқа жағы ағыс бойымен жүргенде
ұлғаяды, ал ұзыны қысқарады, басқаша айтқанда деформация процесі
ағынның қысқа және ұзын жақтарының инверсия бөлімімен өтеді.
Үшөлшемді ағынның көлденең қимасы бірнеше арақашықтықта дөңгелекке
жақындайды, бірақ бұл ағынның тек арадағы және ұзын жақтары орын
ауыстырады.
Көп жағдайда ағыншаның қысқартылған схемасы қолданылады, мұнда аралық
бөлік ұзындығы нөлге тең деп қарастырылады. Егерде есептеулерде аралық
бөлікті ескермесе, онда ол бастапқы бөлікпен сәйкес келген деп қарастырады.

1.2 Үшөлшемді турбуленттік ағыншаның аэродинамикасының
эксперименттік зерттелуі

Алпысыншы жылдар ортасынан бастап көптеген авторлар соплоның
тікбұрышты қимасынан өтетін үшөлшемді турбуленттік ағынды эксперимент
жүзінде оқып үйренуді жүргізіп жатыр, дегенмен бұған дейін бұл
проблеманы эксперимент жүзінде зерттеудің өз алдына басқа да
жолдары болды. Мәселең, параметрінің қатынастары 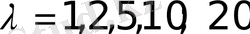болатын
тікбұрышты сопло үшін зерттелген Туркустың үшөлшемді ағыншаға
арналған жұмысын айтуға болады. Мұндай тұжырымның шығуы
зерттеушілердің жазық параллельді турбулентті ағынша үшін алынған
нәтижелерді оқып, үйренуге көп көңіл бөлгендерінің себебінен болып
отыр.
Алғаш рет үшөлшемді ағынның заңдылықтарын оқып үйренудің нақтырақ
эксперименттік жұмыстары Бруклин политехникалық институтының
аэродинамикалық лабораториясында жүргізілді. Үшөлшемді турбулентті
ағындар осьтік жылдамдықтың сөну заңы бойынша үш облыстың бар
екенімен сипатталады.
Бастапқы бөлік (потенциалдық ядро облыс), өткінші бөлік, мұнда
жылдамдықтың ось бойымен өзгеруі саңылау жақтарының қатынастарының
параметрінен тәуелді, ху жазықтығында жылдамдықтың көлденең көрінісі
осыған ұқсастық байқаса, ал ху жазықтығында ұқсамайды; және
сопладан алыс осьтік симметриялы негізгі бөлік (Um~х-1) орналасқан.
Сонымен қатар авторлар тікбұрышты саңылауы және 40 екі
бірдей көлденең бағыттағы (у0,5 және z0,5) шекарасын табу бойынша
орташа жылдамдық өзінің максимал мәнінің жартысына жеткендегі
үшөлшемді ағында деформацияның бар екенін көрсетті. Жіңішке
үшөлшемді ағындарға арналған, қысқа жағына параллель бағытталған
ағынның тегі алғашқыда быраз кемиді; бірақ әртүрлі жылдамдықта
сопланың қимасынан қандайда бір ара қашықтықта олар қиылысып, екеуі
де өседі.
Екі және одан да көп сипаттаулы өлшемі бар үшөлшемді
турбулентті еркін ағындардың әртүрлі тұжырымдардың таралуын
зерттеумен басқа да мектептерді жеке зерттеушілері айналысты.

1.3 Жазық турбуленттік ағыншаның бастапқы бөлігін есептеу

Турбуленттік ағыншаны есептеу үшін Прандтльдің, Тейлордың және т.б.
қарапайым жартылай эмпирикалық турбуленттілік теориялары қолданылады.
Бастапқы бөліктің араласу қабатындағы жылдамдық профилін Прандтльдің
теориясы негізінде ең алғаш Толмин есептеген. Ағынша шетінен ағысталу
схемасы 2-суретте келтірілген.
осі бойынша жылдамдықпен соплодан шығатын турбуленттік
ағынның еркін жарық араласу қабатын қарастырайық. осін сопла
қабырғасына перпендикуляр бағыттаймыз, ал координат басын соплоның екеуіне
орналастырамыз.
Еркін турбуленттік ағыншаны есептеу үшін шекаралық қабаттың
диференциалдық теңдеуін қолдануға болады:

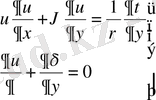(1)

үшін Прандтль формуласын қолданамыз.

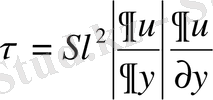(2)

-турбуленттік үйкелістен болатын жанама үйкеліс кернеуі; 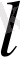-араласу
жолының ұзындығы және .
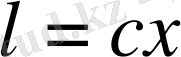(1)жүйені шешу үшін төмендей шекаралық шарттарды қолданамыз.
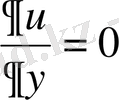
болғанда

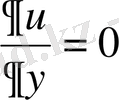
болғанда

2-сурет. Ағыншаның шетінен ағыс схемасы

Араласу қабатында жылдамдық профилі аффинды ұқсас. Сондықтан еркін
шекаралық қабат жайлы есепті төмендегі координаталар бойынша шешуге болады.
х,
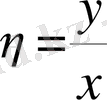
онда өлшемсіз жылдамдық пен -ға тәуелді болады, яғни тек бір
координата функциясы болып табылады.
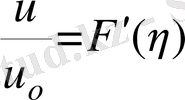(3)
Ток функциясын төмендегідей етіп енгіземіз.
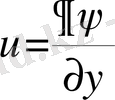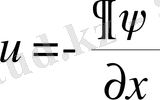, (4)
осыдан
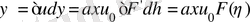(5)
(5) өрнекті у бойынша дифференциалдау арқылы жылдамдық көлденең құраушысын
табамыз
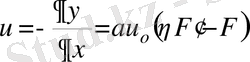(6)
(3) өрнекті қозғалыс теңдеуіне қоя отырып, және
, , ,
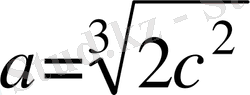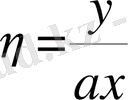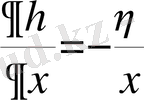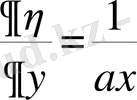
екенін ескере отырып қозғалыс теңдеуін мына түрге келтіреміз.
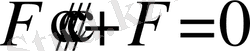(7)
мұндағы штрихтар бойынша туындыны көрсетеді.Бұл формуланы ең алғаш
Толмин алған.
(7) өрнектің шешімі мына түрде болады:
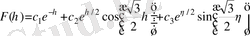(8)
с1, с2, с3 тұрақтыларды есептеу үшін және 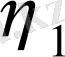мен 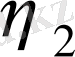-нің мәндерін
табу үшін 5 шекаралық шарт қолдануға болады. Олар ағыншалық шекаралық
қабаттың ішкі және сыртқы шекараларына сәйкес келеді.
а) Араласу қабатының ішкі шекарасына
, , ,
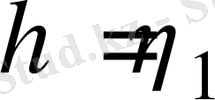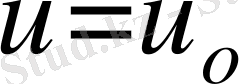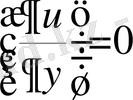
сондықтан (3) пен (6) негізінде
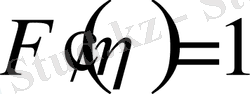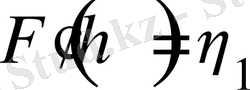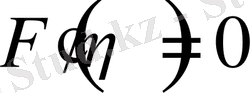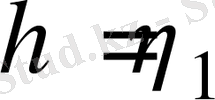, , , (9)
б) сыртқы шекарасында:
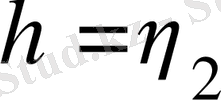болғанда u=0, ,
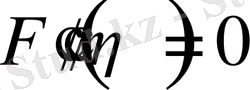
Осы шекаралық шарттарды қолдана отырып, Толмин төмендегі мәндерді алды.

,
, ,
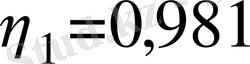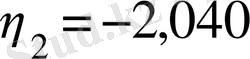
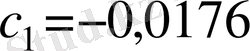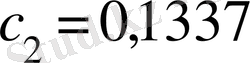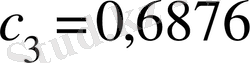
Осы табылған мәндерді (8) өрнекке қою арқылы және дифференциалдау
арқылы араласу қабатындағы өлшемсіз жылдамдық профилін табамыз.
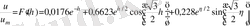(10)
жылдамдық градиенті.
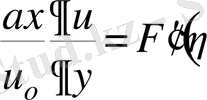(11)
Альтертсонның тәжірибиелік нәтижелерімен салыстыру арқылы ағыншаның
эмпирикалық коэффициенті табылады: . Ағыншаның шекаралық қабатының
толық қалыңдығы

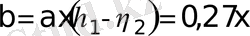
(2) және (3) теңдеулерден және 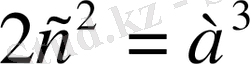екенін ескере отырып, шекаралық
қабаттағы үйкеліс коэффициентін табамыз
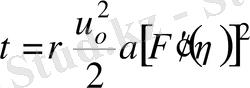(12)

Қабаттың сыртқы шекарасындағы ағын бағыты бойынша иіндік бұрышы

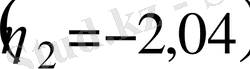
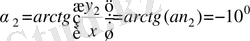(13)

Қабаттың ішкі шекарасындағы бұрыш
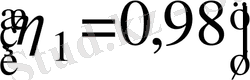
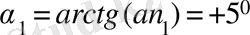(14)

1.4 Жазық турбуленттік ағыншаның негізгі бөлігін есептеу

Жазық турбуленттік ағыншаның бастапқы бөлігін араласу жолының ұзындығы
жайлы Прандтльдің ескі теориясы негізінде Толмин есептеген. Жазық
турбуленттік ағыншаның негізгі бөлігі үшін қарапайым есептеуді Прандтльдің
жаңа теориясы негізінде екі жазық параллель ағын үшін және жазық
турбуленттік ағын үшін Тертлер алған.
Турбуленттік ағыншаның негізгі бөлігінде түрлі қималарында жылдамдық
профильдері аффинды және өлшемсіз жылдамдық профильдері түзу сызық болады.
Профильдің жаңа теориясына сәйкес (2) теңдеудегі араласу жолының
ұзындығы ағыншаның араласу қабатының қалыңдығына пропорционал: және
қималары бойынша жылдамдық градиенті оның орта мәніне тең:
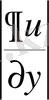( (15)
Осы мәндерді (2) теңдеуге қою арқылы, мынаны табамыз:
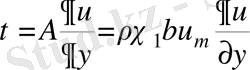(16)
Мұндағы 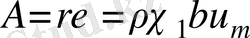- турбуленттік алмасу коэффициенті, араласу зонасының
қалыңдығы, - эмпирикалық тұрақты.
(16) формуладағы -дың мәнін (1) формулаға енгізу арқылы
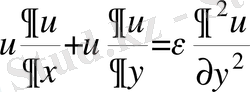(17)
табамыз, мұндағы 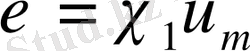-жорамал кинематикалық тұтқырлық коэффициенті, -
ағыншаның ортасындағы жылдамдық.
мен 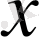арасындағы байланысты табу үшін импульстің сақталу
заңын қолданамыз. Ағыншаның қысымы тұрақты болғандықтан,
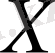осі бойынша импульс құраушыларын ағыншаның барлық көлденең
қималары бойынша интегралдау арқылы мынаны табамыз:
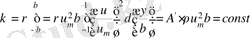(18)

Бұдан

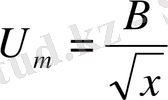(19)
мұндағы - тұрақты шама.
Саңлаудан қашықтықтағы ағыншаның ортасындағы жылдамдықтың
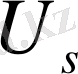деп, осы жердегі ағынша енін 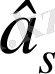деп белгілейміз, онда
, ,
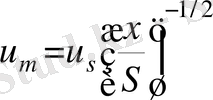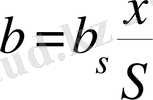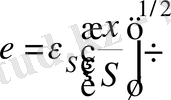
мұндағы
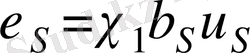
Жаңа айнымалы енгіземіз 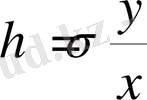, мұндағы -еркін тұрақты.
Үзіліссіздік теңдеуін интегралдау үшін ток функциясын мына түрде
енгіземіз:
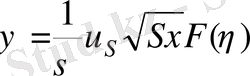, онда

,
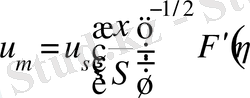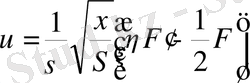
Осы табылған мәнді (17) теңдеуге қою арқылы 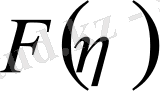функциясын табуға
арналған дифференциалдық теңдеу аламыз:
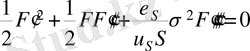(20)

-ны мына түрде алсақ болады:

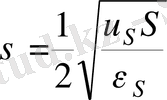(21)

-ның осы мәнін (20) теңдеуге қойып және оны екі рет интегралдаймыз,
сонда
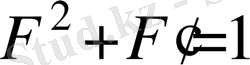(22)

Бұл теңдеудің шешімі келесі түрде болады:
(23)
жылдамдықтың құраушысы:
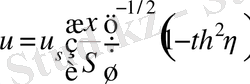(24)
жылдамдықты бірлік ағынша ұзындығына қатысты тұрақты импульс
арқылы өрнектеуге болады, яғни:

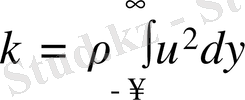(25)

Кинематикалық импульсті 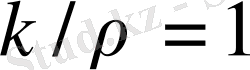енгізу арқылы, соңғы шешімді аламыз:

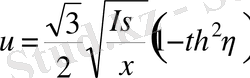
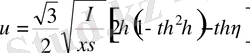(26)

Рейхарттың тәжірибесі нәтижелерімен салыстыра отырып, Тертлер жазық
ағынша үшін эмпирикалық тұрақтының мәнін алды: .
Егер есепке мәнін енгізсек, онда жорамал кинематикалық тұтқырлық
үшін келесі формуланы аламыз.
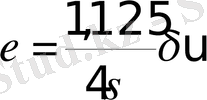
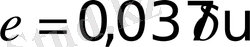-нің мәнін қойып екенін табамыз.

1.5 Жазық еркін ағыншаны эксперименттік зерттеу

Жазық турбуленттік ағыншаны зерттеу үшін саңлаудың шекті ені
және шекті биіктігі , және олардың қатынасы 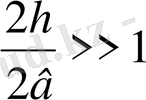болатын
эксперименттік қондырғы құру мүмкін емес. Сондықтан көп жағдайларда олардың
қатынасы 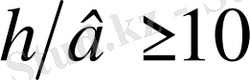мәнімен шектеледі және ағынша екі бүйірінен бір бірімен
қашықтықта жазық пластиналармен шектеледі. Пластиналар 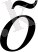және
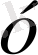остеріне параллель орналасады. Осы кезде егер шектеуші беттердегі
шекаралық қабат қалыңдығы шектеуші пластиналардың арақашықтығынан көп аз
болса, онда ағыс биіктігі шектеусіз соплодан шыққан ағыншаның ағысындай
болады. Немесе саңлаудың биіктігінің еніне қатынасын 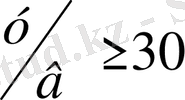түрінде алады
және ағыншаның ортасында ағыс жазық қозғалысқа сәйкес келеді.
Бірінші рет Фертманның [10] жасаған тәжірибесінде тік бұрышты сопло
үшін 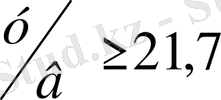болады, мұндағы ені 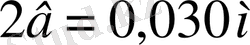және биіктігі 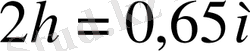. Өлшеулер соплоның
ортасынан 0,75м қашықтыққа дейін жүргізіледі. Осыдан соң осы сияқты
тәжірибиелерді басқа да авторлар жүргізді. Соңғы жұмыстардың 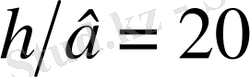болғанда
ағыншаның орталық бөлігінде жылдамдық өрісі биіктігі шексіз саңлаудан
шыққан орташаның жылдамдық өрісіне сәйкес келмеді. Кейбір жұмыстарда
[14,15,16] шыға беріс қимасы тікбұрышты соплодан шыққан ағыншаның ені,
соплоның қысқа қабырғасында, үлкен қабырғасына қарағанда соплодан
қашықтаған сайын тез өсетінін көруге болады.
Ұзындығы шексіз соплодан шығатын ағыншаға жақын ағыншаны алу үшін шыға
беріс қимасы тік бұрышты соплоның қысқа қабырғасын жазық пластиналар мен
шектеу керек. Тәжірибелер көрсеткендей бұл жағдайда, ағыншаның бастапқы
бөлігінде пайда болатын құйынның әсерінен ағыс өрісі жазық турбуленттік
ағыншаның ағысынан өзгеше болады. [8]
Еркін және қабырғалық ағыншалардың бастапқы бөлігінде пайда болған ірі
масштабты когерентті құйындардың дамуы және олардың ағыншаның таралуына
әсері көптеген жұмыстарда зерттелген [11-13]. Тәжірибелер көрсеткендей
ағыншаның бастапқы бөлігінде еркін араласу аймағында дискретті құйындар
пайда болады. Олардың пайда болу жиілігі шекаралық қабаттың еніне және
ағыншаның жылдамдығына байланысты. Соплодан қашықтаған сайын көршілес
құйында бірін бірі қуа отырып, бірігіп өлшемдерін үлкейте береді. Осының
салдарынан ағыншаның бастапқы бөлігінде визуальді картина алу мүмкін емес.
Сондықтан осы жұмыста ағыншаның бастапқы бөлігінде ірі
масштабты құйындардың дамуын және турбуленттік деңгейінің дамуын зерттеуге,
сонымен қатар екі бүйірінен шектеуші пластиналардың жазық және үш өлшемді
еркін ағыншалардың дамуына әсерін термоанемометрлік құралдың көмегімен
зерттеуге мүмкіндік жасалды. Сонымен қатар турбуленттік пульсация
жиілігінің спектрі және ағынша қимасы бойынша турбуленттіліктің алмасу
коэффициентінің таралуы зерттелді

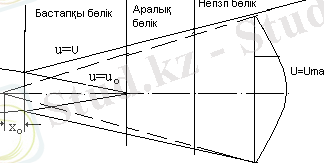
1.6 Жазық турбуленттік ағыншаның жылдамдығының өзгерісіне екі
бүйірінен шектеуші қабырғалардың әсерін зерттеу

Көптеген тәжірибелерден белгілі болғандай жазық турбуленттік
ағыншаның таралуына ірімасштабты құйындар едәуір әсер етеді.
Осындай құйындардың әсерін бақылау үшін ағынша екі бүйірінен жазық
қабырғалармен шектеледі. Егер шекаралық қабаттың қалыңдығы шектеуші
пластиналардың ара қашықтығымен салыстырғанда өте аз болса, онда олардың
ағыншаның орталық бөлігіне әсерін ескермеуге болады.
Эксперименттік нәтижелерден көрініп тұрғандай екі бүйірінен жазық
пластинамен шектелген жазық турбуленттік ағыншаның бастапқы және аралық
бөліктерінде құйындардың екі түрі байқалады. Бірінші жағдайда, ірімасштабты
құйындар шекаралық қабаттың араласу зонасында пайда болып, сопланың
ернеуіне параллель орналасады және шектеуші пластиналарға тіреледі.(3а
-сурет). Жылдамдық профилі мына түрде болады: 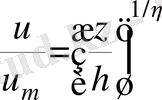, мұндағы: 2h –
шектеуші пластиналардың ара қашықтығы, z – пластиналардан бастап саналады.
Екінші жағдайда ағыншаның бастапқы бөлігінде пайда болған құйындар
тороид тәрізді өзінен өзі тұйықталады.Бұл кезде у осі бағыты бойынша
ағыншаның орталық бөлігі бірден өседі, ал жылдамдық профилі z осі бойынша
біртексіз болып кетеді. Ағыншаның орталық бөлігінде айқын максимум
байқалады. (3б -сурет)
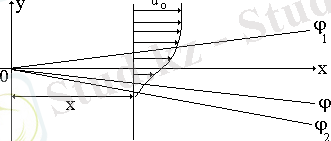
Ені 2b сопладан шығатын у осі бойынша бір бірінен 2h қашықтықта
орналасқан екі пластинаның арасында таралатын жазық турбуленттік ағыншаны
қарастырайық. Ағынша екі бүйірінен жазық пластиналармен шектеледі.
Координат басы сопланың центріне орналастырылған, х осі плстиналарға
параллель бағытталған, у осі ағыншаның бағытымен бағытталған. z осі
шектеуші пластиналарға перпендикуляр бағытталған. (4-сурет)
Х, у жазықтығының орталық бөлігіндегі салыстырмалы жылдамдық профилі
аффинды ұқсас болады және А.С. Гиневский формуласы түрінде келтірілген:
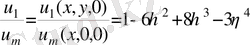(27)
мұндағы 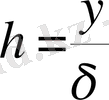, ( – ағыншаның толық жартылай қалыңдығы.
Um(x,0,0) –у,z=0 болғандағы максималь жылдамдық.

a) b)
3-сурет. Шектеуші пластиналардағы жылдамдық профилі
а)2h=30мм: 1-xb=160, 2-100, 3-40, 4-20, 5-n=12
б) 2h=145мм: 1-xb=6, 2-10, 3-16, 4-20

Шектеуші пластиналарға жақын жерде таралатын турбуленттік шекаралық
қабат ағыншаның ортасына жетіп, z осі бойынша жылдамдық таралуы х пен у-тің
берілген мәндерінде дәрежелік тәуелділік түрінде келтіріледі (жазық
каналдағы ағын тәрізді):
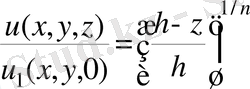(28)
Жазық каналдағы Рейнольдс саныны 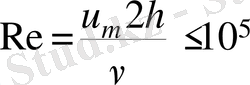n=7 және 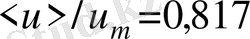болғанда кернеу
үйкелісі мына түрде жазылады:
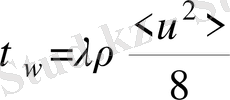(29)
Кедергі коэффициенті Блазиус формуласы бойынша анықталады:
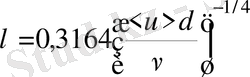(30)
мұндағы d- гидравликалық диаметр. Жазық канал үшін гидравликалық
диаметр шектеуші пластиналардың екі еселенген ара қашықтығына тең:
d=4h (31)
Осы мәнді (29) өрнекке қойып, жазық канал үшін шектеуші қабырғалардағы
үйкеліс кернеуін табамыз:
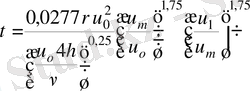(32)
мұндағы: uo, um – ағыншаның қималарындағы бастапқы және максималь
жылдамдықтар.
(27) және (28) формулаларды ескере отырып, өлшемсіз жылдамдықтың
мәнін табамыз:
(33)
Сопладан х қашықтықтағы ағыншаның қималарындағы толық импульс мынаған
тең:
(34)
х және х+dx қималардағы импульстің өзгерісі мынаған тең:
(35)
ағыншаның ені көлденең координатаға пропорционал деп және (32), (33)
формулаларды ескере отырып (35) формуладан мыаны аламыз:
(36)
мұндағы:
(37)
(36) өрнектің оң жағына максималь жылдамдықты нөлдік жуықтауда
түрінде алып, мына өрнекті аламыз:
(38)
мұндағы:
(39)

4-сурет
1-Re=12000, hb=25; 2-Re=35200, hb=14,5; 3-Re=35200, hb=3,0;
4-Re=6060, hb=0,62; тұтас сызық – теория нәтижесі.
(38) өрнектегі жылдамдықтың мәнін (36) формуланың оң жағына тағы да
қойып, екі бүйірінен жазық пластиналармен шектелген жазық ағыншадағы
максималь жылдамдықтың мәнін екінші жуықтауда аламыз:
(40)
мұндағы: ұзындығы шексіз сопладан шығатын жазық ағынша үшін N=3,71.
(40) өрнек бойынша алынған нәтиже мен тәжірибе
нәтижелерінің мәндері 4–суретте келтірілген:
4-суретте сопланың қабырғаларының қатынасы ;3,0;1.66;
болғандағы максиммаль жылдамдық өзгерісінің эксперименттік нәтижелері
келтірілген. Сызық (40) өрнекпен есептелген мәндерге сәйкес келеді.
Суреттен көрініп тұрғандай тәжірибе нәтижелері мен теориялық
нәтижелер бір біріне сәйкес келеді.
Зерттеу мақсатының қойылуы

Бітіру жұмысының мақсаты:
1. Биіктігі шексіз сопладан шығатын жазық еркін турбуленттік ағыншаның
есептеу теориясымен танысу;
2. Ағыншаның бастапқы жылдамдығының таралуына екі бүйірінен шектеуші
пластиналардың әсерін есептеу теориясымен танысу;
3. Екі бүйірінен жазық пластиналармен шектелген жазық турбуленттік
ағыншаның бастапқы бөлігінде пайда болған құйындық құрылымды визуальді
бақылау;
4. Ірі масштабты құйындар пайда болатын жазық ағыншаның бастапқы және
аралық бөліктеріндегі лездік жылдамдықтың таралуын бақылауға қатысу.

2. Турбуленттілікті және екі бүйірінен ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.