Кинематикалық жұптарды жіктеу

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 108 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ

БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

Қ. И. Сәтбаев атындағы

Қазақ ұлттық техникалық университеті

Қ. С. Шоланов, Ж. Т. Жұмашева

МЕХАНИЗМДЕР МЕН МАНИПУЛЯТОРЛАР

МЕХАНИКАСЫ

1-бөлім. Құрылысы және кинематика

Республикалық оқу-әдістемелік бірлестігімен

оқу құралы ретінде ұсынылған

Алматы 2004

Шоланов Қ. С., Жұмашева Ж. Т.

Механизмдер мен манипуляторлар механикасы. 1-бөлім. Құрылысы және кинематика: Оқу құралы. -Алматы: ҚазҰТУ, 2004. 127 б.

ISBN

Оқу құралында «Механизмдер мен манипуляторлар механикасы» курсының бірінші бөлімі аналитикалық суреттеу және үлгілеудің қазіргі заманғы әдістерінің негізінде беріледі.

Материал компьютерлерді қолдана отырып, есептерді шешу үшін ыңғайлы түрде берілген.

Кеңістіктік механизмдер мен манипуляторларға қолданылатын талдау және синтез әдістері қарастырылады.

Роботтық техникадағы қазіргі заманғы жетістіктердің негізінде жаңа параллельді құрылымды манипуляторлар туралы мәліметтер келтірілген.

Оқу құралы «Аспап жасау», «Автоматтандыру және басқару» мамандықтары және сәйкес мамандықтар бойынша оқитын студенттерге арналған. Кітаптағы материалдар машиналар механикасы және роботтық техника саласының магистранттары мен мамандарына пайдалы болуы мүмкін.

Сурет - 35. Кесте - 9. Библиографиялық тізім - 9 атау.

Пікір жазғандар:

Қазақстан Республикасы білім және ғылым министрлігінің 2003 жылғы жоспары бойынша басылады.

ISBN

КІРІСПЕ

Адамның тіршілік әрекетінің барлық салаларында мехатрондық объектілер, яғни қандай-да бір мөлшерде электрондық, электротехникалық және компьютерлік құраушылармен жабдықталған техника - қазіргі заманғы техникалық прогрестің ерекшелік белгісі болып табылады. Өндірісте компьютерлік және сандық программалы басқарылатын қазіргі заманғы станоктар, өнеркәсіптік роботтар және басқа да технологиялық жабдықтар осындай техникалардың мысалдары болып табылады. Үйде немесе кеңседе бейнемагнитофондар, принтерлер, ыдыс жуатын машиналар және құрастырылған микропроцессорлар мен микроэлектрониканың әр түрлі құралдарының салдарынан автоматты түрде жұмыс істеу мүмкіндігі бар басқа да техника қолданылады. Медицинада мехатрондық тәсілдердің негізінде «жасанды жүрек», «жасанды бүйректер», «жасанды аяқтар» және т. б. аппараттар жасалынды және кең түрде қолданылады.

Механика мен электрониканың қиылысындағы жаңа техникалық жетістіктердің бірі - роботтар болып табылады.

Роботтық техника - роботтарды жасауға арналған ғылыми негіз, ғылым мен техниканың жаңа саласы - мехатрониканың негізі болып табылады.

Мехатроника - қозғалысы электроника құралдарының көмегімен басқарылатын және реттелінетін машиналар мен механикалық жүйелерді жасау мен пайдалануға арналған ғылым мен техниканың саласы.

Мехатроника пәнінің тәсілдері мен әдістері - механика, электроника, автоматика және ақпараттану пәндерінің негізінде жасалады.

Жалпы түрде мехатрондық объектілер мен жүйелерге механикалық, басқарылатын және ақпаратты-өлшеу жүйелері кіретінін роботтардың мысалынан көз жеткізуге болады.

Мехатрондық объектінің механикалық бөлігі өз кезегінде қозғалысты түрлендіруге арналған атқарушы қозғалтқыштар мен әртүрлі текті механизмдерді іске қосатын жетектердің жиынтығын құрайтын манипулятор мен атқарушы қондырғылар тәрізді тасымалдаушы жүйеден тұрады.

Ұсынылып отырған оқу құралының мақсаты мехатрондық объектілердің механикалық бөлігін талдау және синтездеу барысында туындайтын, «Машиналар механикасы» немесе «Механизмдер мен машиналар теориясы» дәстүрлі курстарында қарастырылатын есептерге ұқсас механика есептерін, сол сияқты оларды шешу әдістерін мехатроникадан жүйеленген түрде бөле отырып мазмұндау болып табылады. Олардың ерекшеліктері төмендегілер болып табылады:

1) модельдеудің әртүрлі әдістерін қолдану;

2) әрі қарай алгоритмдеу мен компьютерлендіруге негізделген аналитикалық әдістерді қолдана отырып, есептерді шешу;

3) зерттеу объектісі ретінде негізінен көп қозғалмалы және басқарылатын кеңістіктік механизмдер болып табылады;

4) жазық механизмдер кеңістіктік механизмдердің жеке мысалы ретінде қарастырылады.

Ұсынылып отырған оқу құралы негізінен «Аспап жасау» мамандығы және басқа да сәйкес мамандықтар бойынша жоғары білімді бакалаврларды дайындауда қолдануға негізделген. Кітап материалдары механизмдер мен машиналар теориясын, машиналар механикасын, роботтар механикасын оқитындарға, мехатроника облысы бойынша өзінің біліктілігін көтергісі келетін, ой-өрісін және өзінің білімін кеңейткісі келетіндерге пайдалы болуы мүмкін.

1-БӨЛІМ

МЕХАНИЗМДЕР МЕН МАНИПУЛЯТОРЛАРДЫҢ ҚҰРЫЛЫСЫ

1-тарау

Механизмдердің құрылымдық талдауы

1. 1. Негізгі ұғымдар мен анықтамалар

Механизм деп механикалық қозғалысты беру және түрлендіруге арналған байланысқан денелер жүйесін атайды. Классикалық ұғым бойынша механизмдер кіріс буындары деп аталатын және механизмнің басқа да денелеріне қозғалысты беретін, шектелген денелер санынан тұратын өзара байланысқан қатты денелер болып табылады. Механизмнің мысалы ретінде, көптеген іштен жану қозғалтқыштарының ажыратылмайтын бөлігі болып табылатын қосиін-сырғақты механизмді келтіруге болады.

Соңғы уақыттарда роботтардың және басқа да басқарылатын машиналардың пайда болуымен көп қозғалмалы басқарылатын механизмдер жеке класс болып бөлініп шықты. Көп қозғалмалы басқарылатын механизмдердің мысалы ретінде роботтардың атқарушы механизмдері - манипуляторлар болып табылады. Басқарылатын жетектің көмегімен, жүйенің қозғалатын денелерінің әрқайсысының орнының өзгертілуі осы механизмдердің ерекшелігі болып табылады. Дәл осы ерекшеліктер көп қозғалмалы басқарылатын механизмдерге «Механизмдер мен машиналар теориясы» курсы бойынша классикалық оқулықтарда оқытылатын талдау мен синтездеу әдістерін қолдануды талап етеді [1, 2, 3] .

Осы себептен, бұл кітапта қарапайым механизмдерге де, сондай-ақ көп қозғалмалы басқарылатын механизмдерге де қолданылатын механиканың әдістері берілген.

Көптеген жағдайларда көп қозғалмалы басқарылатын механизмдердің мысалы ретінде манипуляторлар қарастырылады. Функционалдық жағынан манипуляторлар да механизмдер болып табылады. Сондықтан да, алдағы уақыттарда қарапайым механизмдер де, манипуляторлар да механизмдер ретінде қарастырылады. Қажеті болған жағдайда, берілген материал қарапайым немесе басқарылатын механизмдерге жататыны ескерілетін болады.

Классикалық ұғым бойынша механизмдер тек қана машиналардың құрамына ғана емес, сондай-ақ мехатрондық объектілердің құрамына да кіреді.

Мехатрондық объектілер (МО) деп - өз ара әрекеттесу және сыртқы ортаға әсері функцияларын орындау үшін, әртүрлі механизмдер мен машиналар, өлшегіш және ақпараттарды өңдеу құралдары және басқару жүйелері біріктірілген жүйені айтамыз. Мехатрондық объектілерге мехатрондық жүйелер және мехатрондық модульдар жатады, ал бір координата бойынша басқарылатын қозғалыс жасайтын мехатрондық объектілер мехатрондық модульдар болып табылады. Мехатрондық модуль ретінде басқарылатын машиналы агрегатты қарастыруға болады. Мехатрондық модульдерден біршама күрделі мехатрондық құрылғылар (МҚ) және жүйелер (МЖ) құрастырылады.

Машина немесе машиналық агрегат деп жұмыс процестерін орындауға қажетті механикалық қозғалыстар мен күш әсерлерін жүзеге асыруға арналған жүйелерді айтады [2] . Белгіленулеріне байланысты машиналардың келесі түрлерін ажыратады:

технологиялық (металлкескіш, ұсталық-баспақ станоктері, өнеркәсіптік роботтар және т. б. ) ;
транспорттық (автомобильдер, тракторлар, көтергіш крандар, мобильді роботтар және т. б. ) ;
энергияның кез-келген түрін механикалық энергияға айналдыратын энергетикалық (іштен жану қозғалтқыштары, турбиналар және т. б. ) ;
ақпараттарды беру, сақтау және түрлендіруге қажетті, механикалық қозғалыстардың орындалуын қамтамасыз ететін ақпараттық (принтерлер, компьютерлердің дисководтері, сканерлер және т. б. ) .

Қазіргі заманғы машиналар МЖ немесе МО айналатындай электроника құралдарымен жабдықталады немесе машиналардың құрамында МО болады. Мысалы, ұшқышсыз ұшақ МО болып табылады, ал ұшқышпен басқарылатын қарапайым ұшақтағы автоматтық навигациясы, басқару және т. б. көптеген жүйелері жеке МО болып табылады. Автомобильдерде МО мысалы болып табылатын автоматтық бүрік жүйесі, автоматтық реттеу жүйесі және т. б. бар. Мехатрондық объектілерде жоғарғы деңгейден түсетін, басқару мақсаты туралы ақпараттар жұмысшы органының немесе механикалық жүйенің басқа да бөліктерінің мақсатты бағытталған механикалық қозғалысына түрленеді. 1-суретте мехатрондық объектінің жұмыс істеу қағидасын түсіндіретін блок-сұлба келтірілген [4] . Мұндағы И1-И7 - берілген жүйенің жекелеген функционалдық блоктарының үйлесу қызметтерін атқаратын интерфейстік құрылғылар. Интерфейс деп берілген жүйенің сыртқы ортамен өзара әсерлесуі үшін және жүйенің өз ішіндегі өз ара әсерлесулер үшін қолданылатын әдістер мен құралдарды айтамыз. И1 интерфейсі қарастырылып отырған МО сыртқы ортамен үйлесуі үшін қажетті аппаратты-программалық және басқа да құралдар кешенін құрайды. Егер басқару мақсаты тікелей оператормен берілетін болса, И1 интерфейсі адам-машина интерфейсін белгілеуі мүмкін. И2 интерфейсі сандық сигналдарды аналогтық сигналдарға түрлендіретін электрондық құрылғылардан және атқарушы жетектерге арналған, сәйкесінше электр кернеулерін жинайтын күш электроникасы блогынан тұрады. И3 интерфейсі әртүрлі механикалық жүйе мен жұмысшы органын жетектермен байланыстыру үшін пайдаланылатын әртүрлі механикалық құрылғылар мен механизмдерден тұрады. И4 интерфейсі микропроцессорлар мен басқару компьютерлері үшін қабылдауға болатын, кері байланыс датчиктерінен сандық белгілерге келіп түсетін аналогтық белгілерді басқару жүйесінің кірісінде түрлендіреді. И5-И7 интерфейстері кіріс айнымалыларының күйі физикалық сипаттамаларына байланысты, механикалық немесе оптикалық, электр аспаптары болуы мүмкін ақпараттық-өлшеу жүйесінің құралдарын құрайды. Блок-сұлбада кері байланыспен басқару жүйесі көрсетілген. МО-ның барлық элементтерінде өздерінің физикалық табиғатына тәуелсіз тек қана аппараттық жанасу ғана емес, сонымен қатар, нақты уақыт режіміндегі МО ішінде ақпараттарды беру және түрлендіру үшін қажетті сәйкесінше программалық қамтамасыз етулер де бар.

МО-ның функционалдық сұлбасынан көрініп тұрғанындай (1-сурет), механизмдер мен көп қозғалмалы басқарылатын механизмдер МО-ның ажыратылмайтын бөлігі болып табылады және онда әртүрлі қызметтер атқарады. МО-ның функционалды бөліктері болып табылатын келесі түрдегі механизмдерді мысал ретінде көрсетуге болады: жетектердің беріліс механизмдерін, манипуляторды, жұмысшы органы бар механикалық жабдықтарды, И3 интерфейсінің механикалық берілістерін, әртүрлі датчиктердің механикалық қосылған жабдықтарын.

Берілген кітапта МО-ны күрделі жүйе ретінде оқып-білу, оның ажыратылмайтын құрама бөлігі - механизмнің талдауы мен синтезінен басталады.

1. 2. Механизмдердің құрылысын талдаудың міндеттері

Механизмде қозғалысты беру және түрлендіруге қатысатын денелер буындар деп аталады. Қарастырылып отырған механизмнің үлгісіне байланысты буындар абсолютті қатты немесе серпімді денелер ретінде қарастырылады. Буындар бірнеше бөлшектерден тұруы мүмкін. Қозғалмайтын буындар тіреуіштер деп аталады. Буындарды кіріс және шығыс, жетекші және жетектегі деп ажыратады.

Бұл кітапта «механизмнің құрылымы» және «механизмнің құрылымдық сұлбасы» тәрізді көпшілік мақұлдаған ұғымдардың орнына сәйкесінше «механизмнің құрылысы» және «механизм құрылысының сұлбасы» ұғымдары қолданылатынын атап кеткен дұрыс. Бұл «Автоматтық басқару теориясында», «Жетектер теориясында» «құрылымдық сұлба» ұғымымен «Механизмдер мен машиналар теориясында» осы терминге басқаларынан ерекше, құбылыстардың өзара байланысын кескіндейтін абстракт кескіннің түсіндірілуімен байланысты. Соңғы уақыттарда механизмдер мен машиналар теориясы бойынша кейбір оқулықтарда «құрылым» терминінің орнына «құрылыс» термині жиі қолданылып жүр.

Механизмдердің құрылымдық талдауының, яғни механизмдердің құрылысын талдаудың негізгі міндеттері - кинематикалық жұптарды жіктеу, механизм құрылысын сипаттау, қозғалмалылықты анықтау, сонымен қатар, механизмдерді толығымен жіктеу болып табылады. Синтездеу есептерін шешуде механизмдер құрылысын талдаудың зор мәні бар және әрі қарай кинематикалық және динамикалық талдау мен синтездеу тәсілдерін анықтайды.

1. 1-кесте

Кинематикалық жұптардың шартты белгілері

1. 3. Кинематикалық жұптарды жіктеу

Механизмнің буындары бір-бірімен салыстырғанда салыстырмалы қозғала алатын өз ара қосылыс түзеді. Жанасқан екі буынның қосылысы кинематикалық жұп (КЖ) немесе мүшелену деп аталады.

Кинематикалық жұптар төменгі және жоғарғы жұптар болып бөлінеді. Буындары өз ара беттер арқылы жанасатын КЖ төменгі жұптар деп аталады. Ал жоғарғы КЖ буындары тек сызық немесе нүкте арқылы жанасады.

Еркін қозғалатын дене кеңістікте алты тәуелсіз қозғалыстар жасайтыны белгілі. Егер екі дене қосылыс түзетін болса, онда олар өз ара өз қозғалыстарына байланыстар деп аталатын шектеулер салады. КЖ түзетін буындардың салыстырмалы қозғалысы (s _r ) санына және байланыстар сипатына тәуелді. КЖ-ны КЖ түзетін буындардың салыстырмалы қозғалысында еркіндік дәрежесінің саны W _r бойынша жіктеу қабылданған. ( r индексі - индексті шама салыстырмалы қозғалыстың көрсеткіші болып табылатынын білдіреді) . Әрине, әрқашанда (екіжақты голономды байланыстар жағдайында)

W _r + s _r = 6 (1. 1)

қатынасы орындалады.

W _r байланысты кинематикалық жұптар бір-, екі-, үш-, төрт-, бес қозғалмалы КЖ болып бөлінеді. Кейбір әдебиеттерде байланыстар санына негізделген кинематикалық жұптарды жіктеудің басқа да түрі параллельді түрде қолданылады. Сонымен, кинематикалық жұптың класы КЖ-ның байланыстар санына тең болады. Мысалы, бір қозғалмалы кинематикалық жұп (1. 1) шартқа сәйкес болатын бесінші кластың кинематикалық жұбы болып табылады. Мысал ретінде, механизмдерде біршама көп кездесетін КЖ 1. 1-кестеде көрсетілген. Сонымен, механизмдер құрылысының жазық және кеңістіктік сұлбаларындағы шартты кескіндерімен төменгі КЖ суреттері келтірілген.

1. 4. Кинематикалық тізбек. Механизмдерді жіктеу

Кинематикалық жұптар арқылы байланысқан буындар жүйесін кинематикалық тізбек (КТ) деп атайды. КТ тұйықталған және тұйықталмаған болып екіге бөлінеді. Егер әрбір буын кем дегенде екі кинематикалық жұпқа енсе, онда мұндай тізбек тұйықталған кинематикалық тізбек деп аталады. Мұндай КТ-да бір және одан да көп өзгертілетін тұйықталған қарам (контур) болады. Қарам деп төмендегі қасиеттерге ие болатын тұйықталған кинематикалық тізбекті атайды:

тізбектің әрбір буыны, оның басқа да екі буынымен КЖ түзеді;

2) қарам 1-қасиетке ие екі басқа қарамның біріктірілу жолымен алынбауы қажет;

3) КТ-дағы тәуелсіз қарамдар саны (k)

k= p-n +1, (1. 2)

Эйлердің топологиялық формуласымен анықталады,

мұндағы p, n - КТ-ғы сәйкесінше кинематикалық жұптар мен буындар саны.

Аралас кинематикалық тізбек тұйықталған және тұйықталмаған кинематикалық тізбектерден тұрады.

Егер бір немесе бірнеше буындарды тіреуіш деп есептесек, онда механизмнің кинематикалық сұлбасы КТ-дан тұрады.

Буындар нүктелерінің қозғалыс траекториясының түріне байланысты механизмдерді көлемдік және беттік механизмдер деп бөлуге болады. Беттік механизмдерге: жазық, сфералық, цилиндрлік механизмдер жатады. Жазық механизмдер буындары нүктелерінің траекториялары жазықтықта немесе параллельді жазықтықтарда жатады. Сфералық немесе цилиндрлі механизмдер нүктелерінің траекториялары сәйкесінше шардың (центрлес шарлар) немесе цилиндрдің (коаксильді цилиндрлер) беттерінде жатады. Талдау және синтездеу әдістерінің қарапайымдылығынан жазық механизмдер тәжірибеде кең таралған. Роботтардың атқарушы механизмдері көлемдік механизмдерге жатады. Көлемдік механизмдерде буындар нүктелерінің көптеген орындары кеңістікте қандай-да бір көлем алуы мүмкін. Мысалы, манипулятордың жұмысшы органының нүктелерінің көптеген орналасулары бар кеңістіктің қандай-да бір бөлігі қызмет ету зонасы деп аталады. Жалпы жағдайда барлық механизмдер кеңістіктік көлемдік механизмдер болып табылады және олардың буындары кеңістікте қозғалады. Жазық механизмдер қойылған есепті кейбір қателіктерге жол бере отырып шешу үшін қабылданатын дәріптеушілік болып табылады.

Құрамына жетекті кинематикалық жұптар кіретін басқарылатын қозғалмалы механизмдер роботтар мен басқа да мехатрондық жабдықтардың атқарушы механизмдері болып табылады. Жетекті кинематикалық жұптар түзетін буындардың салыстырмалы қозғалысы басқарылатын жетектің көмегімен орындалады. Мысалы, егер бір қозғалмалы жетекті кинематикалық жұпта буындардың берілген салыстырмалы қозғалысын жетек жүзеге асырмаса, онда жетекті кинематикалық жұп бір қозғалмалы кинематикалық жұп болмайды, ал кинематикалық жұп түзетін буындар жеке буын болып табылады. Сол себептен, басқарылатын көп қозғалмалы механизмдер басқаратын белгілеріне байланысты жетектің кірісінде әртүрлі уақыт моментінде қозғалмалы буындар мен кинематикалық жұптардың әртүрлі санына ие болуы мүмкін.

1. 5. Механизмдер құрылысының сұлбалары

Механизмдерді зерттеу және жобалау кезінде міндеттерді шешу үшін аналитикалық, физикалық және имитациялық модельдеу әдістерін қолданады. Модельдеу нақты объектіден оның моделіне ауысу болып табылады. Мұндай ауысу қойылған есепті шешу үшін объектінің ең маңызды болып табылатын қасиеттерін бөліп қарастыру және оның жеке ерекшеліктерін абстрактілеу арқылы дәріптеумен байланысты. Ұқсастық теориясы - үлгілеудің теориялық негізі болып табылады. Мысалы, механизмдердің талдауы мен синтездеуі кезінде механизм құрылысының сұлбасы немесе егер буындардың геометриялық өлшемдерін ескеретін болсақ - механизмнің кинематикалық сұлбасы деп аталатын шартты сызба - механизмнің физикалық үлгісі қолданылады.

2-сурет. ІЖҚ механизмдерінің құрылыс сұлбасы

Физикалық үлгілеу, яғни механизм құрылысының сұлбасын құру кезінде буындардың нақты ерекшеліктерін ескермейді және тек қана оның қозғалысты беруге ықпал ететін көрсеткіштерін (пішіндерін) ғана ескереді.

2-суретте іштен жану қозғалтқышының (ІЖҚ) қимасы көрсетілген, ал 2, а- суретте - жұдырықшадан 7, күйентеден 5 және клапаннан 6 тұратын газ таратқыш механизм құрылысының сұлбасы; 2, б-суретте - қосиіннен 1, бұлғақтан 2, сырғақтан (поршеннан) 3 тұратын жазық қосиін-сырғақты механизм құрылысының сұлбасы келтірілген.

3-сурет. Өнеркәсіптік робот және оның манипуляторының құрылыс сұлбасы

Өнеркәсіптік робот (3-сурет) жұмысшы органы - ұстағыштың (4-6 буындар) қозғалмалылығын ескермегенде үш қозғалмалы буындардан тұратын көп қозғалмалы манипулятор болып табылады. 3, а-суретте осы манипулятордың құрылысының кеңістіктік сұлбасы көрсетілген.

Механизмдерді талдау мен синтездеу бойынша алға қойған есептерді ойдағыдай шешу механизм құрылысының физикалық үлгісін дұрыс құруға байланысты екенін атап айтқан дұрыс. Сондықтан да, әртүрлі механизмдердің құрылыс сұлбасын құруға дағдылану маңызды болып табылады.

1. 6. Механизмнің еркіндік дәрежесінің саны. Құрылымдық формулалар

Машиналар механикасында буындардың орнын анықтайтын жалпыланған координаталар санын механизмдердің еркіндік дәрежесінің саны немесе қозғалмалылығы деп атау қабылданған [2] . Бірақ та, көп қозғалмалы басқарылатын механизмдерге қолданғанда, еркіндік дәрежесінің саны және қозғалу дәрежесінің саны жалпы жағдайда сәйкес келмейді. Еркін қозғалатын дене алты еркіндік дәрежесіне ие екені белгілі. Сондықтан да, манипулятордың жұмысшы органы немесе оның кез-келген буыны алтыдан көп еркіндік дәрежесіне ие бола алмайды. Сонымен қатар, кедергіні айналып өтуді қамтамасыз ету немесе жұмыс аумағын кеңейту және т. с. с. мақсаттарда манипулятордың қозғалу дәрежесінің саны керегінше үлкен бола алады. Мысалы, телескопиялық антеннаны ілгерілемелі (призмалық) жұптар түзетін және бір бағыттауыш бойымен қозғалатын, тізбектеліп қосылған буындардан тұратын кинематикалық тізбек ретінде қарастыруға болады. Мұндай жағдайда антеннаның ұштығы оның басқа да буындары тәрізді бір еркіндік дәрежесіне ие болады. Талап етілетін ұзындықты қамтамасыз ету шартымен антеннаның қозғалу дәрежесінің саны бірден үлкен кез-келген бүтін сан болуы мүмкін. Осыған байланысты еркіндік дәрежесінің саны инерциалды санақ жүйесімен (шартты қозғалмайтын) салыстырғанда, қарастырылып отырған буынның (дененің) орнын анықтайтын тәуелсіз көрсеткіштер саны болып табылады. Қозғалу дәрежесінің саны деп жұмысшы органының өзінің қозғалыстарын есептемегенде, басқарылатын көп қозғалмалы механизмнің жұмысшы органының орнын анықтайтын, тәуелсіз мүмкін болатын жылжулардың максималды санын айтады [5, 6] .

Механизмдердің қозғалу дәрежесінің санын анықтау үшін құрылымдық формулалар қолданылады. Жалпы жағдайда қозғалу дәрежесінің саны W

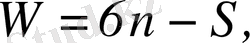
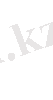(1. 3)

формуласымен анықталады, мұндағы n - қозғалмалы буындар саны, S -буындардың салыстырмалы қозғалысына түсетін КЖ-ның байланыстар саны. (1. 3) формуланы қорыта отырып, байланыстар түспеген әрбір буын басқа бір буынмен салыстырғанда 6 еркіндік дәрежесіне ие болады деп жорамалдайды. n буындардан тұратын жүйенің орнын анықтайтын жалпыланған координаталар саны 6 n -ге тең.

Егер буындар қосылыс түзетін болса, жалпы саны S болатын, жалпыланған координаталар санын байланыстар санына азайта отырып, буындар өздерінің салыстырмалы қозғалыстарына байланыс жасайды:

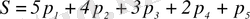, (1. 4)

мұндағы 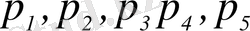- бір-, екі-, үш-, төрт-, бес қозғалмалы КЖ саны.

(1. 3) және (1. 4) формулаларынан Сомов-Малышевтың құрылымдық формуласы

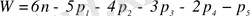(1. 5)

шығады.

Келтірілген ұқсас талдауларға сәйкес жазық механизмдер үшін келесі түрдегі құрылымдық формула шығады:

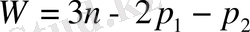. (1. 6)

(1. 6) формула Чебышевтың құрылымдық формуласы деп аталады. (1. 6) формуланы қорытып шығарған кезде, жазықтықта денелер 3 еркіндік дәрежесіне ие болатындығы ескеріледі.

Тұйықталмаған кинематикалық тізбекті манипуляторлар үшін қозғалыс дәрежесінің санын келесі түрдегі формула бойынша жетекті кинематикалық жұптар саны бойынша анықтауға болады:

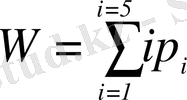(1. 7)