Жазықтықтағы аналитикалық геометрияның негіздері: координаталар, түзулер және сызба әдістері


Мазмұны
3
3. 1
3. 2
Жазықтықтағы түзу және нүкте
Түзулерді сызбада салу
Жазықтықтағы түзу мен нүктеге арналған типтік есептер
Қорытынды
Пайдаланылған әдебиеттер тізімі
16
18
22
Кіріспе
Геометрия тарихынан математиканың аса маңызды тараулары геометриялық салуларға тәуелді болғанын білеміз. Геометриялық салулар теориясы геометрияның негізгі салалары: аналитикалық геометрия, проективтік геометрия, сызба геометрияның пайда болуына байланысты жоғары дәрежеде дами бастады. Салу есебі физика жэне сызу пәндерімен де тығыз байланысты. Физикалық шамалардың өзгерісін графиктік жолмен сипаттауға салу есептері қолданылады. Сызу сабағында оқушылар геометриялық фигураларды салудың кейбір әдістерін нақты практикалық істерінде пайдаланады. Инженерлер мен техниктер кейбір практикалық жұмыстарды графиктер мен сызбалардың көмегімен орындайды. Техниканы дамытуда сызба геометрия, геометриялық салулар, сызбалардың теориясы өте зор рөл атқарады.
Зерттеудің мақсаты. Жазықтықтағы геометриялық салуларды орта мектепте жаңа ақпаратты технологияға байланыстыра оқыту және оқушылардың теориялық және практикалық білімі мен біліктілігін қалыптастыру.
Зерттеудің болжамы : Жазықтықтағы геометриялық салу есептерін шешудің әдістерін (НГО және алгебралық әдістер) үйрету арқылы оқушылардың білімін белгілі бір жүйеге қалыптастыра отырып, олардың логикалық ойлау қабілетін жетілдіру.
Зерттеудің пәні. Жазықтықтағы аналитикалық геометрия.
Зерттеудің міндеттері.
1. Оқытудың жаңа технологияларының элементтерін енгізу.
2. Аналитикалық геометрия және алгебралық әдістердің негізгі критериясын анықтау.
3. Сабақ сапасын арттыру арқылы, оқушылардың ізденуін және таным деңгейін жоғарылату.
1. Жазықтықтағы аналитикалық геометрияның элементтері
1. 1 Аналитикалық геометрия. Декарттық координаталар системасы
Аналитикалық геометрия геометриялық бейнелерді алгебралық әдістермен зерттейді. Аналитикалық геометрияның негізгі құралы XVII ғасырда Декарт енгізген координаталар әдісі болып табылады.
О нүктесінде қиыласатын, кесінділерді өлшеу бірліктері бірдей болатын өзара перпендикуляр екі О х , О у түзуді тік бұрышты координаталар системасы деп атайды. О х осін абсцисса осі деп, О у осін ордината осі деп атайды.
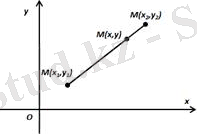
Тік бұрышты координаталар системасын кейде Декарттық координаталар системасы деп те айтады. О ху координаталар системасында берілген М нүктесінің координаталары х, у (х, у сандары суретте көрсетілген кесіндінің ұзындықтары арқылы анықталады) сандары болса, онда ол нүктені М (х; у) деп белгілейміз. Мұнда х - нүктенің абсциссасы, у - нүктенің ординатасы.
Декарттық координаталар системасында М 1 (х 1 ; у 1 ), М 2 (х 2 ; у 2 ) нүктелері берілсін. Олардың ара қашықтығы төмендегі формуламен есептеледі:
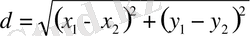 (1)
(1)
1-сурет - Декарттық координаталар системасы
Бір түзудің бойында жатпайтын үш нүкте үшбұрыш анықтайтынын мектеп курсынан білеміз.
Теорема. Бір түзудің бойында жатпайтын кез-келген үш нүкте А(х 1 ; у 1 ), В(х 2 ; у 2 ), С(х 3 ; у 3 ) анықтап тұрған үшбұрыштың ауданы мына формуламен есептеледі:
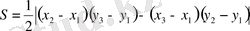 (2)
(2)
Айталық, жазықтықта М 1 М 2 кесіндісі берілсін, М осы кесіндінің кез-келген М 2 - ден басқа нүктесі болсын. М нүктесі М 1 М 2 кесіндісін λ қатынасында бөліп тұрсын, яғни:
(1)
М 1 (х 1 ; у 1 ), М 2 (х 2 ; у 2 ) нүктелері анықтап тұрған кесіндіні λ қатынасында бөлетін М(х; у) нүктесінің координатасын төмендегі формулалар арқылы есептеуге болады:
(2)
λ=1 болғанда кесіндінің ортасы болып тұрған нүктенің координатасын табатын формула шығады:
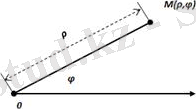
Кей жағдайларда Декарттық координаталар системасынан басқа координаталар системасын қолдану ыңғайлырақ болады. Сондай координаталар системасының бірі - полярлық координаталар системасы.
Полярлық координаталар системасында М нүктесі полюс деп аталатын О нүктеден қашықтығы (ОМ=ρ) мен ОМ кесіндінің полярлық ось деп аталатын ОЕ түзуімен жасайтын бұрышы φ арқылы анықталады. ОМ кесіндісін нүктенің полярлық радиус-векторы деп атайды. Егер полярлық осьтен полярлық радиус-векторға қарай бұрылу бағыты сағат тіліне қарсы бағыт болса, онда бұл бұрыш оң таңбалы болады, кері бағытты теріс бағыт деп есептейді.
Нүктенің декарттық координаталары мен полярлық координаталары арасында мынадай байланыс бар (полярлық осьті абсцисса осі деп есептейміз, ал ордината осі полярлық осьпен оң бағытта 90 градус бұрыш жасайды) .
(3)
(4)
Аналитикалық геометрия - геометрияның қарапайым геометрия бейнелерді (түзулер, жазықтықтар, қисықтар, екінші реттік беттер) координаттар әдістерінің негізінде алгебралық амалдар арқылы зерттейтін бөлімі.
Координаттар әдісінің пайда болуы 17 ғасырда астрономия, механика және техника ғылымдарының дамуымен тығыз байланысты. Координаттар әдісі мен аналитикалық геометрияның негіздері Р. Декарттың «Геометриясында» (1637) мейлінше толық және анық баяндалған. Бұл әдістің басты идеялары оның замандасы П. Фермаға да белгілі болған. Аналитикалық геометрияның бұдан әрі дамуына Г. Лейбниц, И. Ньютон және Л. Эйлер зор үлес қосқан. Аналитикалық геометрияның тұжырымдарын Ж. Лагранж аналитикалық механика, ал Г. Монж дифференциалдық геометрия негіздерін қалау барысында пайдаланған.
Координаттар әдісінің мәні - жазықтықта орналасқан кез келген М(х, у) нүктесін декарттық координаттар жүйесі арқылы анықтауға болатындығында. х және у шамалары О ху жүйесіндегі М нүктесінің декарттық тік бұрышты координаттары (не қысқаша тік бұрышты координаттар) деп аталады. Осыған сәйкес оларды М нүктесінің абсциссасы (х) және ординатасы (у) деп атайды.
2-сурет - Жазықтықтағы координаттар
Жазықтықтағы координаттар әдісінің негізгі идеясы - L сызығының геометриялық қасиеттерін осы сызықты сипаттайтын Ғ(х, у) = 0 теңдеуін аналитикалық және алгебралық жолмен зерттеу. Жазықтықтағы аналитикалық геометрияда 1 және 2-реттік алгебралық сызықтар жүйелі түрде зерттеледі.
1-реттік сызықтар - түзу сызықтар және олар бір дәрежелі:
А х + В у + С = 0 алгебралық теңдеуімен,
ал 2-реттік қисық сызықтар:
Ах 2 + В ху + Су 2 + D х + Е у + Ғ = 0 теңдеуімен сипатталады.
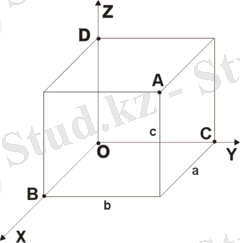
2-реттік қисық сызықтарға эллипс, гипербола, парабола қисықтары жатады. Табиғатта өте жиі кездесетін бұл қисықтардың негізгі қасиеттері аналитикалық геометрияда толық анықталған. Кеңістіктегі аналитикалық геометрия координаттар әдісі жазықтықтағы әдіске толық ұқсас етіп қарастырылады. Мұнда кез келген М нүктесі х - абсцисса, у - ордината және z - аппликата координаттары арқылы анықталады. Кеңістікте орналасқан S бетін O xyz координаттар жүйесіне қатысты F = (x, y, z) = 0 теңдеуімен сипаттауға болады. Кеңістіктегі аналитикалық геометрия А х + В у + С z + D = 0 теңдеуімен анықталатын 1-реттік беттердің (жазықтықтардың) және Ах 2 + Ву 2 + Сz 2 + D ху + Е уz + Ғ хz + G х + Н у + М z + N = 0 теңдеуімен анықталатын 2-реттік беттердің (эллипсоидтың, гиперболоидтың, параболоидтың) қасиеттері зерттеледі.
Қазақстанда аналитикалық геометрияның дамуына профессорлар А. З. Закарин, Ф. Д. Крамер, В. В. Стрельцов, доценттер С. А. Аяпбергенов, М. У. Исқақов, Ж. Ш. Юсупов, Э. И. Хмелевский, т. б. айтарлықтай үлес қосты.
Анықтама. А х +В у +С=0 теңдеу түзудің жалпы теңдеуі деп аталады.
Мұндағы к = - түзудің бұрыштық коэффициенты. Бағыттауыш векторы (түзуге параллель), М 0 (x 0 , y 0 ) нүктесін басып өтетін түзуінің теңдеуі .
Нормаль векторы, М 0 (x 0 , y 0 ) нүктесін басып өтетін түзуінің теңдеуі A(x-x 0 ) +B(y-y 0 ) =0.
Бұрыштық коэффициенті к белгілі және М 0 (x 0 , y 0 ) нүктесін басып өтетін түзуінің теңдеуі y-y 0 =k(x-x 0 ) .
Берілген екі нүкте М 1 (x 1 , y 1 ) және М 2 (x 2 , y 2 ) нүктелері өтетін түзудің теңдеуі.
Координаталар өстерін А(a, 0), B(0, b) нүктелерінде қиып өтетін түзудің теңдеуі.
1. 2 Жазықтықтағы аналитикалық геометрияның қарапайым есептері
Түзудін бойынан еркімізше бір О нүктесін алсақ, онда сол түзудін бойындағы кез келген М нүктесі ОМ кесінді аркылы анықталады. Бұл М нүктесі О нүктесінің не оң, не сол жағында жатуы мүмкін. М нүктесінің О нүктесіне қатысты екі жағдайын қарастырайық. О нүктесінін сол жағындағы нүктені М 1 оң жағындағы нүктені М 2 деп белгілейік.

1-сызба
Егер О нүктесінен оңға қарай алынған ОМ 2 кесіндісін оң таңбалы болсын десек, онда О нүктесінен солға карай алынған ОМ 1 кесіндісі теріс танбалы болады. Мұндай өзінің ұзындығымен және таңбасымен сипатталатын кесінді бағытталған кесінді деп аталады.
Егер m белгілі бір бірлік өлшемі үшін алынса, онда әрбір кесінді осы бірлік арқылы өлшенеді, яғни берілген ОМ кесіндісінің m бірлік өлшемге қатынасынан бір сан шығады:
(5)
Берілген кесіндіні өлшейтін m бірлік өлшемді масштаб деп атаймыз. Масштаб m= 1 болса, онда х = ОМ. Егер М нүктесі М 1 жағдайда болса, онда х теріс таңбалы сан болады:
Егер М нүктесі М 2 жағдайда болса, онда х он таңбалы сан болады:
Түзудін бойындағы кез келген нуктені аңықтайтын шарттардың киындысын түзудің бойындағы координаталар жүйесі дейміз. Қарастырылып отырған жағдайдағы кез келген нүкте (М) координатаның бас нүқгесінен (О) сол нүктеге (М) дейінгі қашықтықтың масштабқа қатынасымен анықталады. Түзудің бойындағы мұндай координаталар систем асы декарттың координаталар жүйесі деп аталады.
Түзудің бойындағы кез келген М нүктесінің координатасын х деп атасақ, онда осы нүкте мен оның координатасының өз ара сәйкестігін мынаңдай символмен белгілейміз: М(х) . Бүл символ М нүктесінің координатасы х болады деген мағынаны береді, яғни М нүктесі х координатасы арқылы берілді деп ұғу керек. Сонымен, түзудің бойындағы кез келген нүкте жалғыз санмен аныкталады, яғни бір нүктеге бір-ақ сан сәйкес, керісінше айтқанда, бір санға ылғи бір нүкте сәйкес келеді.
Егер х-тің мәні нольден бастап оңға қарай түзудін бойымен шексіз өсе берсе, онда х айнымалы шама болады, ал оның өзгерілуін мынандай белгімен жазамыз: х = 0, х= + ∞, яғни 0 < х < + ∞. Сол сияқты айнымалы шама нольден бастап солға қарай шексіз кемитін болса, онда былайша белгіленеді: х = 0, х = - ∞, яғни - ∞ < х < 0 немесе 0 > х > - ∞.
Енді түзудің бойындағы х-тің толып жатқан сансыз мәндерін жалпы түрде белгілeyгe болады: - ∞ < х < + ∞
Бас нүктенін координаталары ылғи нольге тең, яғни О(0), х = 0. «Нүктені табуң деген сөзді онын ылғи «координатасын табуң деген мағынада түсіну керек.
х координатасының мәні (1) қатынасымен аныкталатынын көрдік. Ал координатаны сызбада көрсету үшін оны былайша жазуға болады:
ОМ=х (1 /// )
2-сызба
Бұл жағдайда ОМ=х бағытталған кесінді емес, сол бағытталған кесіндіні өлшейтін сан. Өйткені мұнда алынып отырған масштаб ылғи бірге тең (m=1) және осыған сәйкес нүктелердің координаталарын бірыңғай бір координаталар жүйесымен алып отырмыз.
Түзуге он бағыт беріліп, оның бойынан бір О нүктесі белгіленіп және бірлік өлшем - масштаб алынса, онда мүндай түзу координаталық ось деп аталады. Түзудің оң бағыты көрсетілсе, онда ол ось деп аталады.
Кесіндінің бағыты осьтің бағытыменбірдей, яғни ңүктенің қозғалысы бас нүктеден онға қарай саналады. М 1 , М 2 және М 2 М 1 кесінділердің ұзындықтары бірдей, ал бағыттары әр түрлі, таңбалары қарама-қарсы. Өзінің ұзындығымен және таңбасымен сипатталатын кесіндіні бағытталған кесінді дегенбіз. Бағытталған кесінділер былайша белгіленеді: М 1 М 2 , М 2 М 1 . Бағытталған кесіндінің ұзындығы модуль деп аталады. Осьтің бойымен оң таңбамен алынған кесіндінің щамасы немесе абсолют мәні бағытталған кесіндінің ұзындығы делінеді. Кесіндінің абсолют мәні былайша белгіленеді: М 1 , М 2 , М 2 , М 1 . Мына М (х) нүктенің х координатасын ОМ-нің абсолют мәні дейміз.
Теорема. М 1 , М 2 , М 3 нүктелері остің бойына қандай болып туссе де, ылғи мынадай теңдік орындалады:
М 1 М 2 + M 2 M 3 = М 1 М 3
Дәлелдеу. х осінің бойында бұл үш нүкте мынадай алты жағдайда (4-сызба) болуы мүмкін:
1) М 1 М 2 М 3 ;
2) М 1 М 3 М 2 ;
3) М 2 М 1 М 3 ;
4) М 2 М 3 М 1 ;
5) М 3 М 1 М 2 ;
6) М 3 М 2 М 1 ;

3-сызба
Бірінші жағдайда М 1 М 2 , М 2 М 3 , М 1 М 3 кесінділерінің ұзындықтары М 1 М 2 , М 2 М 3 , М 1 М 3 кесінділеріңің ұзындықтарына тең. Тендіктің дұрыс екендігі төртінші сызбаның біріншісінен айқын көрінеді, өйткені М 1 М 2 , М 2 М 3 кесінділерінің қосындысы М 1 М 3 , кесіндісіне тең.
Екінші жағдайды біріншіге келтірейік:
М 1 М 3 + М 3 М 2 = М 1 М 2
Осыдан М 1 М 3 = М 1 М 2 - М 3 М 2 . Ал М 3 М 2 = - М 2 М 3 (өйткені M 3 M 2 мен М. 2 М 3 - тің таңбалары карама-қарсы) . Сондықтан М 1 М 3 = М 1 М 2 + М 2 М 3 .
Қалған төрт жағдайларды осы сияқты дәлелдеуге болады. Осы теоремаға сүйеніп 4, 5, 6, . . . , п нүктелері осьтің бойына қандай болып түссе де. мынадай теңдіктін дүрыс екендігін көрсету қиын емес:
М 1 М 2 + M 2 M 3 + M 3 M 4 + . . . + М n-1 М п = М 1 М п .
Теорема. Осінің, бойындағы бағытталған кесіндінің ұзындығын табу үшін кесіндінің соңғы нүктесінің координатасынан бірінші нүкіенің координатасын алу керек.
Дәлелдеу. Бізге х осінің бойында жатқан М 1 (х 1 ), М 2 (х 2 ) нүктелері берілсін. М 1 М 2 - бағытталған кесінді. Теорема бойынша осьтің бойындағы О, M 1 , M 2 нүктелерінің 4-сызбадағы жағдайына сәйкес : ОМ 1 + М 1 М 2 = ОМ 2 . Осыдан М 1 М 2 = ОМ 2 ОМ 1 .
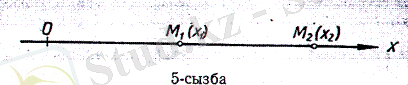
4-сызба
Теореманың шарты бойынша бізге берілгені: ОМ 2 = х 2 , ОМ 1 = х 1 .
Табу керек: М 1 М 2 . Ал М 1 М 2 = х 2 -х 1 .
Осыдан М 1 М 2 кесіндінің ұзындығы, яғни М 1 (х 1 ), М 2 (х 2 ) нүк-телерінің арасындағы қашықтық М 1 М 2 кесіндісінің абсолют мәніне тең, яғни М 1 М 2 = М 1 М 2 = х 2 - х 1 . Ал бағытталған кесіндінің (M 1 М 2 ) шамасын табу үшін ақырғы координата мен бастапқы координатаның айырымын алу керек. Сондықтан түзудің бойындағы кез келген екі нүктенің арасындағы кашықтык мынадай формуламен жазылады: М 1 М 2 = х 2 - х 1 немесе d=x 2 - х 1 .
2. Жазықтықтағы нүктенің координаталары
Жазықтықта бір-біріне перпендикуляр болатын Охпен Oy остерін қарастырайық. Бұл осьтердің қилысатың О нүктесі екі оске жалпы координаталық бас нүкте болсын. Горизонталь Ox осін абсцисса осі деп, вертикаль О у осін ордината осі деп атайық. Абсцисса осінің оң бағытын О бас нүктесінен оңға қарай, ал ордината осінің оң бағытын О нүктесінен жоғары қарай алайық. Сонда осы екі оң бағыттардағы координаталардың таңбалары плюс (+), ал бұл бағыттарға қарама-қарсы координаталардың таңбалары минус (-) болады. Осы қиылысқан екі ось жазықтықты төртке (І, ІІ, ІІІ, ІV) бөледі.
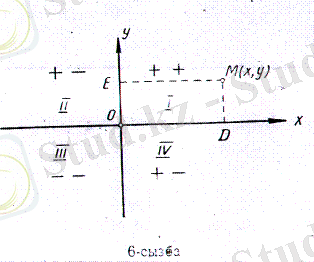
5-сызба
Бірінші ширектегі нүкте координаталарының таңбалары ылғи плюс. Екінші ширектегі абсцисса таңбасы минус, ординатаныкі плюс. Үшіншісінде екеуінікі де минус, төртіншісінде абсцисса таңбасы плюс, ординатаныкі минус.
6-сызба
Координаталар жазықтығынан бір М нүктесін алып, сол нүктеден осьтерге перпендикуляр түсірсек, онда М (х, у) нүктесінің координаталары x = OD, у-DM болады. х пен у сандары М нүктесінің координаталары деп аталады. Бұдан біз мынаны көреміз: жазыктықта бір нүкте берілсе, онда онын координаталары беріледі. Баскаша айтқанда, жазықтықтағы әрбір нүкте екі санмен (x = OD, y = DM) анықталады. Сөйтіп, жазыктыкта әрбір нүктеге екі сан сәйкес келеді, керісінше екі санға ылғи бір нүкте сәйкес болады.
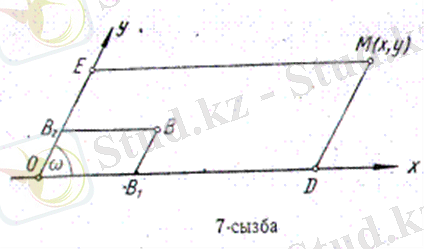
О х пен О у осьтерінің бойындағы кесінділерді өлшеу үшін әр түрлі масштаб, яғни абсцисса осі үшін m l = OB 1, ордината осі үшін m 2 =ОВ 2 алуымыз керек. Басқаша айтқанда, әрбір осьтін бойынан еркімізше әр түрлі бірлік өлшеуіш алуға болады. Сонда М нүктесінің координаталары мынадай екі тендік аркылы жазылады:
(6)
(7)
Абсцисса мен ордината осьтері координаталар осьтері деп аталады. В мен В 2 нүктелерінің орнына Внүктесін алуға болады. Масштабы еркімізше алынған координаталар жүйесын аффиндік координаталар жүйесі деп атайды. Егер осы екі осьтің (О х , О у ) бойындағы кесінділер бір масштабпен өлшенсе, яғни m 1 = m 2 = ОВ 2 = ОВ 1 = m болса, онда координаталар жүйесы декарттык, координаталар жүйесі деп аталады. Егер екі осьтін, (О х , О у ) арасындағы бұрыш ω еркімізше алынса, ондай жүйе қиғаш бурышты координаталар жүйесі деп аталады. Егер бұрыш ω = π/2 болса, ондай жүйе тік бұрышты немесе ортогональдық координаталар жүйесі деп аталады. Біз тік бұрышты декарттық координаталар жүйесін пайдаланамыз.
Декарттык координаталар жүйесі болу үшін мынадай шарттар:
1) координаталардын, бас нүктесі;
2) осьтердің оң бағыттары;
3) ұзындықтың бірлік өлшеуіші (масштабы) берілу керек.
Масштабты бірге тең (m = 1) деп алған қолайлы болады.
7-сызба
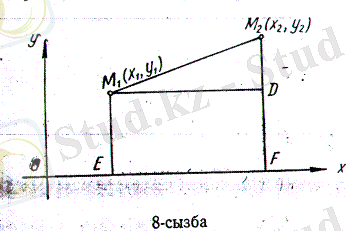
Жазықтықтағы екі нүктенің ара қашықтығы. Жазықтықта М 1 (х 1 , у 1 ), М 2 (х 2 , у 2 ) екі нүктесі берілсін. Осы екі нүктенің ара қашықтығын табайық.
Берілген М 1 , М 2 нүктелерінен абсцисса осіне М 1 Е және М 2 Ғ перпендикулярын түсірейік. Онан кейін М 1 нүктесінен абсцисса осіне параллель M 1 D сызығын жүргізсек, онда M 1 M 2 D тікбұрышты ұшбұрышы шығады. Осы тік бұрышты үшбұрыштан Пифагор Теоремасы бойынша (M 1 D) 2 + (DM 2 ) 2 =(M 1 M 2 ) 2 болады. Осы кесінділердің ұзындықтарын нүктелердің координаталары арқылы жазайық:
ОЕ = х 2 , ЕМ 1 = у 1 , ҒМ 2 = у 2 , EF= M 1 D = x 2 --x 1 , DM 2 = y 2 -y 1 .
Тік бұрышты үшбұрыштың M 1 D, DM 2 катеттері мен М 1 М 2 гипотенузасының орнына олардың координаталар арқылы шыққан мәндерін қойып, екі нүктенің ара қашықтығының формуласын табамыз:
(8)
Егер осы нүктелерді басқа ширектерден алсақ та, формула өзгермейді, өйткені координаталардың айырымдары (х 2 -х 1 ), (у 2 - у 1 ) қандай таңбалы сандар болса да, олардың квадраттары (х 2 -х 1 ) 2 , (у 2 - у 1 ) 2 ылғи оң таңбалы сандар болады.
Кешенді сызбада жазықтық төмендегі тәсілдермен беріледі:
8-сызба - Бір түзуде жатпайтын үш нүкте арқылы
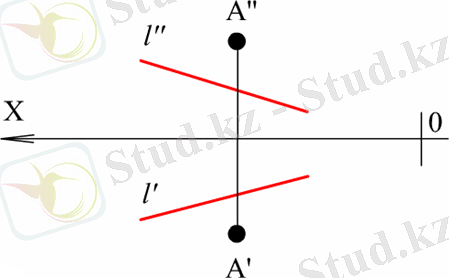
9-сызба - Түзу және оның бойында жатпайтын нүкте арқылы:
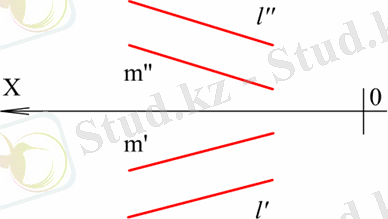
10-сызба - Екі параллель түзумен

11-сызба - Екі қиылысатын түзумен
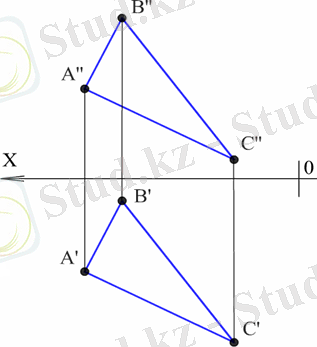
12-сызба - Кез келген жазық пішінмен (үшбұрыш, шаршы, шеңбер және т. б. )
Көрнекі түрде жазықтық проекция жазықтықтарын қиып өтетін түзулер көмегімен кескінделеді. Қандай да бір жазықтық проекция жазықтықтарын қиып өтетін түзулер жазықтықтың іздері деп аталады.
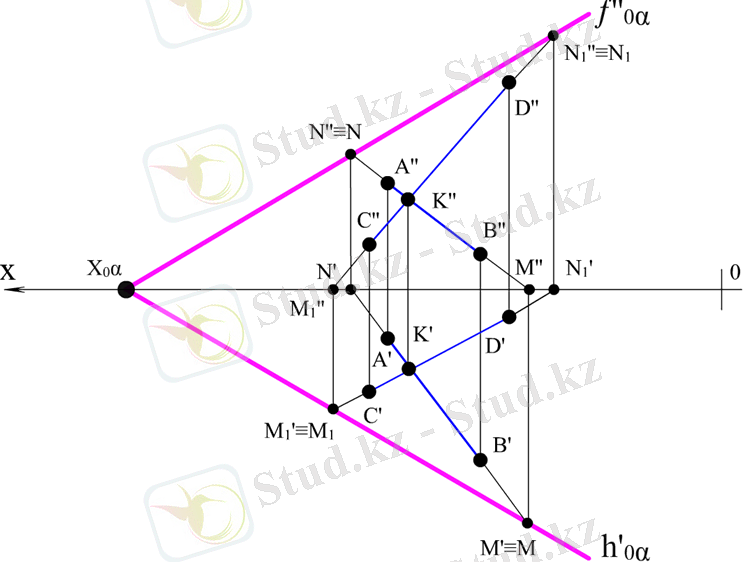
13-сызба - Жазықтық іздері h'oα -α жазықтығының горизонталь ізі f"oα -α жазықтығының фронталь ізі Xoα - α жазықтығының іздерінің тоғысу нүктесі
3. Жазықтықтағы түзу және нүкте
Нүкте - координаттары бар, бірақ өлшемі, массасы, бағыты жоқ, ешқандай геометриялық немесе физикалық қасиеті жоқ кеңістіктегі абстракт нәрсе.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz