Шектелген элементтердің типтері

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 36 бет
Таңдаулыға:

Мазмұны

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
1. Есептің қойлымы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
2. Шекті элемент әдісі туралы қысқаша түсініктеме ... ... ... ... ... ... ...
3. Шекті элемент әдісін қолданатын компьютер жүйесінің көрінісі ... .
3.1. ANSYS ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
3.2. NASTRAN ... ... ... ... ... ... ... ... ... ... ... ... ... .
3.3. APM WinMachine ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
3.3.1. Есептеу кезіндегі қолданатын негізгі теңдеулер
4. ЗПС-250 тістіилемдейтін орнақтың бүрлегішінің модельін құру және

есептің орындалуы
... ... ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
.
4.1.Бүрлегіш білігінің шекті элемент
үлгісі ... ... ... ... ... ... ... . ... .
4.2. Кернеулі-деформация күйдегі статикалық есептеу ...
4.3. Өзіндік тербеліс түрі мен жиліке есептеу
... ... ... ... ... ... ... ..
4.4. Мәжбүр тербеліске есептеу
... ... ... ... ... ... ... ... ... ... ... ... ... ...
4.5. Тіреудің жылжыуынан біліктің жүктелуін анықтау және есептеу...
4.6 Оң және сол бүрлегіш білігінің есептеу кезіндегі негізгі нәтижесі
5.Қортынды ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
6. Әдебиеттер тізімі
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
...

Кіріспе

Шынжырлы берілістердегі жұлдызша тістерін ыстық илем мен жасауда
бұқаралық өндірісте көптісті күрделі тісжонғыш білдектерді салыстырмалы
қарапайым тісилемдейтін орнақпен алмастыруда үлкен экономикалық әсерге
жетуге болады .Сонымен қатар металды үнемдеу, басқа техналогияларды
қолдануда үлкен көлемде жоңқа шығыны шығады . Тісті доңғалақтарды және
жұлдызшалы берілістерді илемдеумен дайындағанда техналогиялық күш
кедергілерінің характерлерімен қарастырсақ орнақтың шпинделіне иілу мен
бұралу тербелісін туғызады : соңғылары илемдеудегі дайындаманың кескінінің
дәлдігін төмендетіп , бұйымды жасауда және дайындауда радиалды дүрсілдерді
, дәлдіксіз диаметр және шеңберлік адымның өзгеруін туғызады . Белгілі бір
тісті жұлдышаларды илемдегенде жұмыс режимінің сәйкес еместігін тудырып ,
дайындама дәлдігін сақтау қамтамасыз етілмейді .
Нағыз жұмыс мақсаты өнімділікті арттыру жолдарын іздеу және динамикалық
сапаны жақсарту арқылы орнаққа дәлдік қамтамасыз ету .
АРМ WinMachine жүйесін қолдану арқылы статистикалық және гормоникалық
жүктеулерде бүрлегіштердің біліктерінің иілу дефорормациясы есептеліп
нәтижесі шығады.

2. Шектелген элементтер әдісінің негіздері және қолдану саласы; негізгі
түсініктер.

ШЭӘ пайда болуы ғарыштық зерттеулердің (1950 ж.) есептерін шешуімен
байланысты.Бұл әдіс құрылыс механикасынан және серпімділік теориясынан, ал
содан соң ғана бұл әдісті вариациялық-айырымды деп атайтын және оның
математикалық табиғатын ерекше бөліп айтатын математиктермен негізделген
болған. Олар ШЭӘ-нің математикалық негіздеуімен айналысады, яғни оның
нәтижелерінің дәл келуінің және дұрыс болуының теориялық талдауын жасайды.
Дәл сол уақытта, инженерлік тәжірбиеде жиі қолданылып жатқан әдістердің
қатал негіздемелеріне көңіл бөлмей зерттеушілер қиын техникалық есептердің
шешімін тауып жатыр, ал құрастырылған алгоритмдер мен бағдарламаларды
белгілі нақты шешімдермен тексереді.
ШЭӘ өзінің жетілуінде, потенциалдық энергияны минималдау жолымен есепті
сызықтық теңдеулер деңгейлерінің жүйесіне әкеле алатын құрылыс
механикасында белгілі Рэлея-Ритца әдісінің бір нұсқасы ретінде қарастыруға
болатындығы дәлелденгеннен кейін (1963 ж.) айтарлықтай алға жылжыды.
ШЭӘ-нің минимизациялау рәсімімен байланысы техниканың өзге
салаларындағы есептерді шығару кезінде оны кең түрде пайдалануға мүмкіндік
берді. Әдіс Лаплас немесе Пуассон (мысалы, электромагниттік өрістер)
теңдеулермен сипатталатын есептерге қолданылған. Бұл теңдеулердің шешімі,
сондай-ақ кейбір функционалды минимизациялаумен байланысты. Бұл әдістің
көмегімен жылу таратылуының есептерінің, гидромеханика есептерінің, және
жеке жағдайларда кеуекті ортада сұйықтықтың ағуы жөніндегі есептердің
шешімдері белгілі.
ШЭӘ-нің қолданылу саласы, құрылыс механикасының, жылу таратылуының,
гидромеханиканың есептеріндегі элементтерді анықтайтын теңдеулер Галеркин
әдісі немесе ең кіші квадраттар тәсілі сияқты өлшенген байланыссыздар
әдісінің осындай нұсқаларының көмегімен жеңіл алынуы мүмкін. Бұл нақты
деректің белгіленуі ШЭӘ-нің теоретикалық негізделуіне негіз болды, өйткені
дифференциалды теңдеулердің көптеген типтерінің шешімі кезінде оның
қолданылуына мүмкіндік берді. Сонымен, құрылыс механикасы есептерінің
сандық рәсімдерінен шығатын ақырғы элементтердің әдісі дифференциалды
теңдеулердің немесе дифференциалды теңдеулер жүйелерінің саңдық шешімдердің
жалпы әдісіне айналды. Бұл прогресске жедел әрекетті ЭЕМ-ның (ЭВМ)
жетілгендігінің арқасында шағын уақыт аралығында жетті.
ШЭӘ-нің айтарлықтай нақты әрі толық пайда болу тарихы және қолданбалы
теориясы жұмыстарында айтылған.
ШЭӘ-нің мазмұны және оның тәжірбиелік асырылуының негізгі кезеңдерін
қысқаша сипаттап өтейік.
Шетелген элементтер әдісінің негізгі идеясы, кез келген үзілмейтін
көлемді (ауысу, температура, қысым және т.с.с.) жеке элементтерден
(учаскелерден) тұратын үлгісімен аппроксимациялауға болатындығынан тұрады.
Осы элементтердің әрқайсысында зерттелетін үзілмейтін өлшем,
қарастырылып жатқан элементтің шектелеген нүктесінде зерттелетін үзілмейтін
өлшем мәндерінде құрастырылатын бөлшекті-үзілмейтін функциясымен
аппроксимицияланады.
Жалпы жағдайда үзілмейтін өлшем алдын-ала белгісіз, және осы өлшемнің
мәнін ауданның кейбір ішкі нүктелерінде анықтау қажет, ол үшін ауданның
кейбір ішкі нүктелерінде осы өлшемнің сандық мәндері белгілі болса (әрі
қарай осы нүктелерді түйіндер деп атаймыз). Осыдан кейін жалпы жағдайға
көшүге болады.
Үзілмейтін өлшемнің дискретті үлгісін жасау үшін көп жағдайларда келесі
әдістерді қолданады:
1. Үзілмейтін өлшемнің анықталу ауданы, элемент деп аталатын
ауданшалардың шекті санына бөлінеді. Бұл элементтердің ортақ түйінді
нүктелері бар және жинақталғанда ауданның пішінін аппроксимицияламайды.
2. Қарастырылып жатқан ауданда нүктелердің шекті саны бекітіледі. Осы
нүктелер түйінді нүктелер немесе түйіндер деп аталады.
3. Үзілмейтін өлшемнің мәні әрбір түйінді нүктеден бастан бастап ақ
белгілі болып саналады, алайда осы мәндерді нақты жағдайда есептің
физикалық мағынасына байланысты қосымша шектеулерді салу жолымен анықтау
керектігін естен шығармау қажет.
4. Түйінді нүктелерде зерттеліп жатқан үзілмейтін өлшемнің мәндерін
және осы немесе басқа аппроксимицияланатын функцияны пайдаланып ауданның
ішіндегі зерттеліп жатқан мәнін анықтайды.
Жоғарыда айтылғанды, стреженің ішіндегі температураның таралуын зерттеу
үлгісінде түсіндірейік. Жалпы жағдайда температураның таралуы белгісіз, ал
біз осы өлшемнің кейбір нүктелердегі мәнін анықтағымыз келеді. Дискретті
үлгісін жасау әдістемесі жоғарыда сипатталғандай болып қалады, бірақ оған
қосымша бір қадам қосылады. Алдын ала стерженің бойындағы кейбір
нүктелердегі температураның мәні белгілі болды деп санайды. Алдын ала
белгісіз болғандықтан енді ауыспалы болып табылатын осы түйіндердегі
көптеген түйіндерді және температураның мәндерін анықтайды. Аудан (біздін
жағдайда – стерженің ұзындығы) элементтерге бөлінеді, оның әрқайсысы үшін
аппроксимицияланатын функция анықталады.
Температураның түйінді мәндері, шектік жағдайларды есепке алып (мысалы,
шыбықтың ұштарындағы температураның мәндері) шыбық бойындағы температураның
дәл таралуына ең жақсы жақындауын қамтамасыз ететіндей таңдалуы тиіс. Осы
таңдау, есептің физикалық құрамына байланысты кейбір өлшемді
минимизациялау жолымен жүзеге асады. Егер қарастырылатын есеп жылудың
таралуы болса, онда сәйкес дифференциалды теңдеумен байланысты функция
минимизацияланады. Минимизациялау процессі, температураның түйінді
мәндеріне қатысты алгебралық сызықтық теңдеулердің жүйелерін шешуге
әкеледі. Орын ауыстыру, дефформациялар және кернеу өрістері анықталатын
өзге есептерде деформацияланған дененің потенциалды энергиясы
минимизацияланады.
Аппроксимирацияланатын функциялар көбінесе сызықтық, квадраттық немесе
кубтық полиномдар түрінде таңдалады әрбір элемент үшін өз полиномын
таңдауға болады, бірақ полиномдар элемент шекараларының бойымен өлшемнің
үзілмеуін сақталатындай іріктеп алынады. Осы элементпен байланысты бұл
полиномды элементтің функциясы деп атайды.
Бұл көзқараспен қарасақ түйінді нүктелердің ақырғы санында
біріктірілген құрылымдық элементтердің кейбір жиынтығы ретінде қарауға
болады. Әрбір жеке элемент үшін күш пен орын ауыстырулар арасындағы
қатынастар белгілі болса, онда құрылыс механикасының әйгілі әдістерін
қолданып қасиеттерді сипаттауға және құрылымның қылығын зерттеуге болады.
Жаппай ортада байланыс нүктелерінің саны шексіз, және осы серпімділік
теориясында сандық шешімдердің негізгі қиындығын құрайды. шектелген
элементтер түсінігі, элементтердің шекаралары бойымен үйлестірілген беттік
кернеулерге эквивалентті фиктивті күштер ендірілетін түйінді нүктелерде
ғана өзара әрекеттесетін тұтас денені бөлек бөлшектерге бөлу жолымен осы
қиындықтан өтудің бір жолы болып саналады. Егер осындай идеализация рұқсат
етілсе, онда есеп, сандық жолмен шешілуі мүмкін, құрылыс механикасының
кәдімгі есебіне ұқсас.
Сонымен, ШЭӘ-ні пайдаланған кезде берілген аудан үшін шектік есептің
шешімі, кейбір ауданшаларда (шектелеген элементтер) анықталған функциялар
жиынтығы түрінде ізделеді.

2.2 Тәжірбиелік жүзеге асырылудың негізгі кезеңдері

Сонымен, ШЭӘ-не сәйкес күрделі пішінді құрылымның үлгісі аумағында
жақындатылған шешімдер ізделетін салыстырмалы қарапайым пішінді анағұрлым
кішкентай бөліктерге (шектелген элементерге) бөлінеді. Осындай модельдеудің
нәтижесі болып, тұтас құрылымдағы кернеулер мен ығысулар өрісі табылады.
Сонымен, ШЭӘ-ін пайдаланумен есептің шешімі келесідегідей негізгі
этаптардан тұрады (2.1-Сурет):

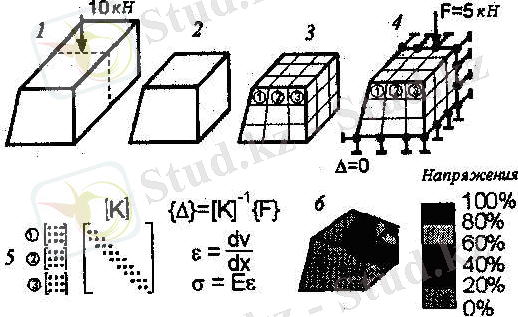
1) Есепті бірегейлеу, оған атау беру; құрылым сызбасын және
жүктемелерді жасау;
2) ШЭӘ-сі үшін жарамды геометриялық үлгісін жасау;
3) үлгіні шектелеген элементтер торына бөлу;
4) шекаралық жағдайлардың үлгілердің қосымша (кинематикалық шекаралық
жағдайлар, яғни шекарада бекіту, және күштік шекаралық жағдайлар, яғни
шекаралардағы жүктемелер);
5) теңдеулер жүйесінің сандық шешімі (автоматты);
6) нәтижелерді талдау.
1, 2, 3, 4-кезеңдер препроцессорлық деңгейге, 5-кезең – процессорлық
деңгейге, 6-кезең – постпроцессорлық деңгейге жатады.
Салынған үлгі жеткілікті қарапайым пішінді шектелген элементтерге
бөлінеді. Шектелген элементтердің бірнеше типтік пішіндері бар, оларда
ығысулардың өрісі бірнеше интерполяциялық функциялардың көмегімен
түйіндердің ығысулары бойынша анықталады. Осындай әдіспен есептелген
ығысулар бойынша кернеулер мен деформациялардың өрісін анықтайды.
ШЭӘ-нің көмегімен есеп шығарудың ең қиын кезеңі – бұл препроцессорлық
(preprocessor) дайындық деңгейі кезінде ақтық-элементтік үлгіні жасау,
өйткені элементтер торының автоматтық құрылуы қателердің мүлдем болмауына
кепілдік бермейді. Жүктемелерді және шектік жағдайларды дұрыс салу сондай
ақ айтарлықтай қиындықтар тудырады.
Жоғарыда айтылған элементтердің бесіншісі (теңдеулер жүйесінің сандық
шешімі) автоматты түрде орындалады, және, қағида бойынша, айтарлықтай
қиындық туғызбайды (қатқылдық матрицасы нашар негізделген жүйелерді
санамағанда).

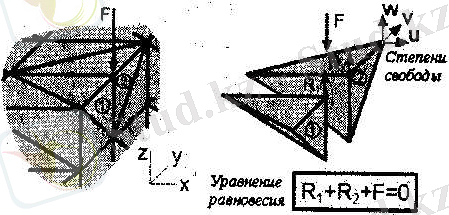
Алтыншы кезең (нәтижелердің талдауы) нәтижелерді көзбен көрудің
инструменталды құралдарымен айтарлықтай жеңілдетіледі.
Шектелген-элементтік есептерде түйіндердегі ауысулар белгісіз
екендігін, сондай-ақ үшөлшемді есептерде тетрогональді элементтің әрбір
түйінінде үш бағыт бойынша ауысуы мүмкін екендігін (2.2-Сурет) есептеп,
матрица түрінде жазылған тепе-теңдік теңдеулерінің жүйесі 100000 жететін
және одан асатын өлшемге ие болуы мүмкін. Алайда, қазіргі кездегі ЭЕМ (ЭВМ)
үшін осындай теңдеулер жүйелерінің шешімі толығымен оңай есептеледі.Тепе-
теңдік теңдеулерін құрған кезде, координаттық осьтердің әрқайсысына барлық
күштер проекциясының сомасы нөлге тең екендігі, ал ішкі күштердің сомасы
кері таңбасы бар сыртқы күшке тең екендігі ескеріледі.
Үшөлшемді модельдерде әдетте түйіндердің саны элементтер санынан артық,
ал еркіндік дәрежелерінің саны түйіндер санынан 3 есе артық (кинематикалық
типтік жағдайлардың санын есепке алмағанда).
Қатқылдық матрицасы [K] түйіндік ығысулардың векторларын {U} және
жүктемелерін {F} байланыстырады.

2.3 Шектелген элементтердің типтері

ШЭӘ-нің негізгі концепциясынан, құрылымның жалпы үлгісі (немесе оның
жеке бөліктері) өзара төбелерінде (түйіндерде) қосылған көптеген шектелген
элементтерге бөлінетіндігі шығады (2.3 а,б-Сурет). Күштер түйіндердің
ішінде әрекет етеді. Шектелген элемент абсолютті қатты дене болып
табылмайды.

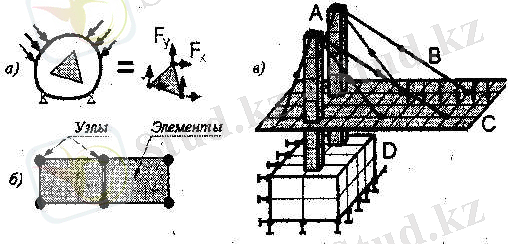
шектелген-элементтік әдістеме, кернеулер мен деформациялар берілген
шектелген элементтен тыс жерде де болатындығы мүмкін дейді.
Шектелген элементтердің анағұрлым жиі қолданылатын бірнеше типтері бар
(2.3-Сурет); (А) білеу, (В) стержен, (С) жіңішке пластина немесе қабықша,
(D) екіөлшемді немесе үшөлшемді дене. Үлгіні жасаған кезде бір емес бірнеше
элементтер типтері қолданылуы мүмкін.
ШЭӘ-сі бойынша есептеулердің дәлдігі көптеген факторларға байланысты,
соның ішінде шектелген элементтердің санына да. Алайда, егер үлгі ішінде
кернеулері айтарлықтай өзгермесе, онда шектелген элементтердің саны
кернеулерді есептеп шығару дәлділігіне қатты әсер етпейді.
Шектелген элементтер сызықтық (бірінші кезектің элементтері) немесе
параболалық (екінші кезектің элементтері) болуы мүмкін (2.4-Сурет).
Сызықтық элементтердің жақтары түзу болады және түйіндері тек қана бұрышта
болады. Сонымен, үшөлшемді элемент түйіндерінің минималды саны 4-ке тең.
Параболалық элементтердің әр жақтың бойы бойынша аралық түйіні болуы
мүмкін. Осының арқасында элементтің жақтары қисықсызықты (параболалық)
болуы мүмкін. Элементтердің саны бірдей болған кезде параболалық элементтер
санаулардың дәлірек мәнін береді, өйткені олар үлгінің қисық сызықты
геометриясын анағұрлым дәлірек көрсетеді және пішіннің анағұрлым дәлірек
функциясына (аппроксимицияланатын функциялар) ие болады. Алайда, жоғары
тәртіпті шектелген элементтерді қолдануымен есептеу үлкен компьютерлық
ресурстарды және үлкен машиналық уақытты талап етеді.
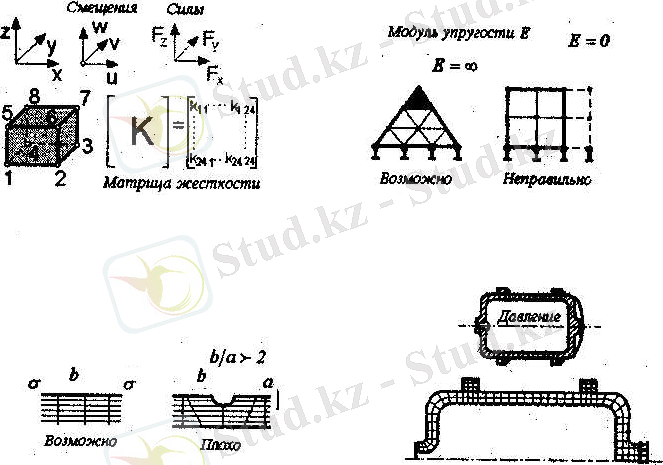түйіндері бар ең қарапайым үшөлшемді сызықтық элементті қарастырайық
(2.5-Сурет). Түйіндердің әрқайсысында еркіндіктің 3 дәрежесі бар. Бұл 24
түйіндік ығысуларды және тұра сондай түйіндік күштерді қарастыру қажеттігін
білдіреді. Осылайша, түйіндік ығысулардың векторын түйіндік күштердің
векторымен байланыстыратын қатаңдық матрицасының [К], өлшемділігі [24 х
24] болады.
Қатаңдық матрицасының құраушылары серпімділік модуліне тұра
пропорционалды. Сонымен, серпімділіктің нөлдік модулі шектелген элементтің
жоқтығын білдіреді (2.6-Сурет). Бұл жағдайда серпімділіктің нөлдік модульге
бөлуі айтарлықтай ақаулықтарға келтірілген.
Серпімділіктің шексіз үлкен модулі берілген элемент абсолютті қатты
болып табылады. Бұдан басқа, егер серпімділік теориясы шексіз кернеулерге
рұқсат етсе (мысалы, саңылаудың төбесінде), онда ШЭӘ-дегі кернеулер барлық
жағдайларда шектлген болып саналады.
Элемент жақтарының арасындағы қатынасқа қатысты келесідегілерді атап
өтуге болады. Егер ығысулардың, дефформациялардың және кернеулердің үлкен
градиенттері күтілмесе, яғни кернеу шоғырландырғыштарының әрекет ету
аумағынан алысырақ жақтарының қатынасы 2 және одан артық Ұзын
элементтерді (2.7-Сурет) қолдануға болады.
Егер құрылым мен жүктемелер осьінеқатысты симметриялық болса, мысалы,
(2.8-Сурет) көрсетілгендей, есеп жазық симметриялы шектелген элементтердің
көмегімен шешілуі мүмкін.

2.4. Шектелген элементтердің торын салу
Шектелген – элементтің талдаудағы анағұрлым маңызды кезендерінің бірі
болып шектелген элементтерден құралған тордың үлгісіне құрылымдалуы болып
табылады, яғни тұтас үлгінің кішкентай бөлшектерге бөлінуі (шектелген
элементтер), өзара түйіндерде байланысқан.
ANSYS программалық жиынтықта тор құрудың екі негізгі әдісі бар: еркін
тордың құрылуы (2.9,а-Сурет) және реттелген тордың құрылуы (2.9,б-Сурет)
Еркін тор автоматты түрде құралады, осындайда көршілес элементтер
айтарлықтай өлшемдері бойынша ажыратылуы мүмкін (2.9,а-Сурет). Реттелген
тор үлгінің геометриялық элементтерінің бөліктердің кейбір санына бөліну
жолымен құралады (2.9,б-Сурет). Элементтердің саны көп автоматты түрде
салынған торлардың құрамында түйіндердің саны элементтердің санынан көп.
Түйіндер мен элементтер арасындағы қатынас жуықтап алғанда жазық еркін
торлар үшін 2:1 және төртқырлы элементтері бар еркін үшөлшемді торлар үшін
6:1.
Анығы, шектелген элементтің өлшемі қаншалықты кіші болса (h) (2.10-
Сурет) үлгідегі элементтер саны сол ғұрлым көп көп болады, бұл орайда
есептеудің уақыты анағұрлым үлкейеді, ал талдаудың қателіктері азаяды.
Алайда, қателер нөлге дейін кішіреймейді, өйткені элементтер санының көбеюі
мен ЭЕМ-ғы (ЭВМ) дөңгелектеу қателіктері көбейеді.
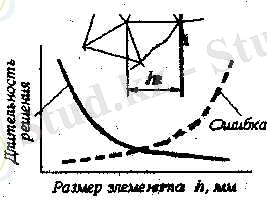ШЭӘ-н қолданумен есептерді орындау тәжірбиесі көрсеткендей, шектелген
–элементтінің торын құру кезінде келесі ұсыныстарды ұстану керек (2.11-
Сурет): 1) сызықтық элементтер квадраттық элементтерге (аралық бір түйіні
бар) немесе кубтық элементтерге (аралық екі түйіні бар) қарағанда жиірек
торды талап етеді; 2) реттелген тор (б) еркін торға (а) қарағанда жиірек
қолданылады; 3) 4 түйіні бар тікбұрышты тор үшбұрышты элементтері бар (б)
торға қарағанда жиірек қолданылады; 4) аралық түйіндері (г) бар үшбұрышты
элементтердің торы 4 түйіні бар тікбұрышты элементтердің торынікі сияқты
дәлділігі бар; 5) 8 түйіні бар тікбұрышты тор (д) тікбұрышты элементтерінің
үлкен өлшеміне қарамастан аралық түйіндері бар (г) үшбұрышты элементтердің
торына қарағанда жиірек қолданылады; 6) кубтық полиноммен ығысудың
аппроксимациясы ұсақ торды қажет етеді.
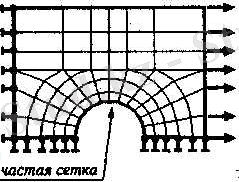
ШЭӘ-сі жақындатылған әдіс екендігін естен түсірмеу қажет, олардың
дәлділігі шектелген элементтердің типтерін және өлшемдерін дұрыс таңдауға
байланысты. Осылайша, мысалы, дефформациялардың немесе кернеулердің үлкен
градиенті күтілетін жерден жиірек тор талап етіледі (2.12-Сурет). Сол
уақытта анағұрлым жиірек тор азды-көпті дефформациялары немесе кернеулері
бар аумақтарда, сондай-ақ айтарлықтай қызықтығы жоқ аудандарда қолданылуы
мүмкін. Осымен, байланысты зерттеуші кернеудің шоғырлану ауданын алдын-ала
білуге тиіс.
Айтпақшы, талдау нәтижелерінің дәлділігі, егер кернеулер
шоғырландырғышының қасындағы көршілес элементтердің өлшемдері тіпті ұқсас
емес болса азаяды. (2.13-Сурет).

Шектелген элементтердің пішіні, сондай-ақ есептеулердің дәлділігіне
ықпал етеді, сондықтан тіпті жіңішке және созылған элементтерді қолданбау
керек (2.14-Сурет), өйткені жақтары жуықтап алғанда бірдей элементтер аздау
қателік береді.

Орналасуымен, пішінімен және өлшемдерімен байланысты қателіктер
жөніндегі қосымша мәліметтер Х.2.6 т-да келтірілген Нәтижелердің
дәлділігі. Торда бір уақытта үшбұрышты және төртбұрышты элементтер болуы
мүмкін, алайда олардың арасында саңылаулар болмау тиіс (2.15-Сурет).
Болашақта элементтерді торға біріктіру үшін торларды реттік санмен
нөмірлейді. Бұрыштары 180о –тан үлкен төртбұрышты элементтерді салуға
болады (2.16-Сурет).

2.5 Шекаралық жағдайлар

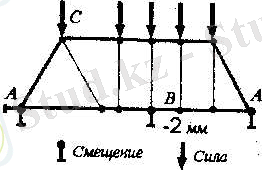
Шекаралық жағдайларды беру шектелген-элементтердің талдауың
жауапкершілігі мол деңгейлердің бірі. Осылайша, мысалы, (2.17-Сурет)
көрсетілген үлгілердің бірінде А және В түйіндеріндегі графикалық шектін
бейнеленген жағдайлар, үлгісі көрсетілген түйіндерінің ығысулары шектеулер
байланыстарының салынуын ескере отырып нақты құрылымның тұра сол
түйіндерінің ығысуларын сәйкес болуы үшін қызмет атқарады.
Бұл орайда ығысулар нөлдік (А түйінінде), сондай-ақ нөлдік емес (В
түйініде) мәндерге ие болуы мүмкін. Сондай-ақ шекаралық жағдайлар бар, олар
болған кезде жүктемелер беріледі (С түйіні).
Шекаралық жағдайлар (ығысулар немесе күштер) түйіндерге ғана
салынады.(2.18-Сурет). Түйінге салынған шекаралық жағдайлардың максималды
саны оның еркіндік дәрежесінің санына тең – 3 күштер немесе 3 ығысулар.
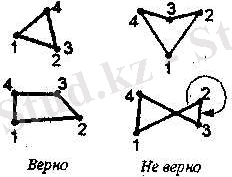
Маңызды шекаралық жағдайлардың саны минималды қажет аз да емес көп те
емес болуы тиіс. Осылайша, мысалы, элементтің әрбір түйінінде еркіндіктің
барлық дәрежелерін белгілеу қажет емес (2.19,а-Сурет): сондай-ақ түйіннің
ішіндегі күшті, берілген түйінде ығысу белгіленген тұра сол бағытқа салмау
керек (2.19,б-Сурет); қандай да бір осьтердің бойымен бекітулердің болмауы
(2.19-Сурет) талдау кезінде осы ось бойымен сандық есептер кезінде
дөңгелектеудің болмауы мүмкін емес қателіктерінің салдарынан көрінетін
ығысуларға әкелуі мүмкін. Қарастырылған мысалдар үшін шекаралық
жағдайлардың дұрыс сұлбалары (2.19-Сурет) көрсетілген.
Шекаралық жағдайлардың орналасу сұлбасы жүктеудің түріне байланысты
(созылуы, таза иілуі, ығысу), (2.20-Сурет) көрсетілгендей.
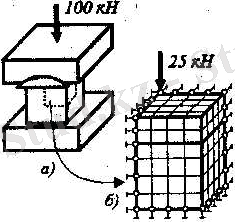Егер құрылымның симметрияның осьтері немесе жазықтары болса, онда
шекаралық жағдайларды тағайындау кезінде оны ескеру қажет. Осылайша,
мысалы, қатты пуанссондары бар анағұрлым жұмсақ біртекті материалдан
жасалған кубты қысатын пресс симметрияның үш жазықтығына ие болады. Бұл
жағдайда, құрылымды тұтастай үлгілеудің қажеттілігі жоқ екендігі белгілі.
Симметрия жазықтықтарындағы нүктелер де сәйкес ығысулар нөлге тең екендігін
ескеріп, үлгілеудің бөліктерін ғана үлгілеуге болады (14 немесе 18). Бұл
жағдайды, симметрия жазықтықтарында жататын элементтердің түйіндерінде
сәйкес шекаралық жағдайлармен ескеру керек. (2.21,б-Сурет)
Егер Сен-Венан принципін көңілге алсақ, торды құру кезінде элементтер
мен шекаралық жағдайлар өлшемдерінің таңдалуын айтарлықтай жеңілдетуге
болады: екі статикалық эквивалентті күш жүйелері көлденең қиманың сызықтық
сипаттық өлшемінен үлкен (ba, 2.22-Сурет) олардың салыну нүктелері
қашықтығында кернеулердің бірдей өрісін жасайды.
Келесі жағдайды қарастырайық. Тым үлкен созылатын кернеулер көптеген
бұзылулардың негізгі себебі болып саналатындығы белгілі. Бұл жағдайда, егер
максималды созылатын кернеулердің аумағы күштің салыну нүктесінен алысрақ
орналасса (мысалы, 2.23-Сурет сұлбасындағыдай) осы нүктенін қасынан
элементтердің егжей тегжейлі торын құрудың қажеттіліг жоқ, өйткені осында
негізінен қысатын кернеулер әрекет етсе.

2.6 Нәтижелердің дәлділігі

ШЭӘ-сі де жататын сандық талдау нақты құрылымның кейбір идеализациясын
талап етеді. Сондықтан, есептеуіш техникасының күрт өсуіне қарамастан ШЭӘ-
сі бойынша есептеулердің нәтижелері қателіктерден босамайды. Есептеуіш
техникасын есептеудің негізгі процесстерін және кезендерінде түсінбей Қара
жәшік ретінде пайдаланылуы айтарлықтай қателерге әкеліп соғуы мүмкін.
Өкінішке орай операторлардың қателесуін де есептен шығармау керек.
Шектелген-элементтердің талдауға кіріспес бұрын инженер төмендегілерді
түсіну керек:
- берілген есеп талдаудың қай саласына жататындығы;
- тұтас құрылымның қай бөлігі нақтырақ тексерілуі керек екендігі;
- берілген есепте қай жеңілдіктерге жол беруге болатындығы.
Әрине, бұл зерттеушінің қажетті классификациясын талап етеді.
Қателер шектелген-элементтердің талдаудың кез келген стадияларында тууы
мүмкін; есепті қою, дискретизациялау (үлгіні құру кезінде), сандық
шешілулер кезінде.
Есепті дұрыс қоюдің қателіктері, шектелген элементтердің таңдалған типі
немесе олардың өлшемі материалдың құрылымда физикалық қылығына сәйкес
келмеген жағдайда пайда болуы мүмкін. Бұл қателікті, тордың автоматты
құрылуын пайдаланып біршама кішірейтуге болады (тым болмаса, шектелген
элементтің өлшемімен байланысты бөлігін). Алайда, есептерді қою кезінде
қателердің негізгі көзі болып, шекаралық шарттардың дұрыс емес берілуі
табылады. Сонымен, шектелген – элементтік талдаудың дұрыс шешілуі,
шекаралық шарттар үлгісіне дәл жасалуынан, нақты құрылымның геометриясынан
және материалдың қасиеттеріне байланысты.
Дискретизациялау қателері, нақты құрылымды шектелген элементтердің
(олардың пішіндерін және өлшемдерін ескеріп) шектеулі санымен ауыстыру
кезінде пайда болады.
Теңдеулер жүйелерінің сандық шешімімен байланысты қателер, әдетте
жоғарыда айтылып өткен қателердің екі типіне қарағанда онша мәнді емес.
Шектелген-элементтік талдау кезінде, қағида бойынша, ығысулар белгісіз
болып табылады, және бұл жағдайда шешімнің нәтижесі болып {u} түйініндегі
ығысулар векторы болып табылады. Элементтің өзге нүктелеріндегі ығысулар
интерполяциямен есептеледі.
Аппроксимациядан кейін ығысулардың өрістері (элемент шегінде) пішін
функциясы деп аталатын сәйкес полиноммен деформациялар мен кернеулер
есептелуі мүмкін. Есептеулердің сипатталған сұлбасы, түйіндердегі
ығысуларды анықтаған кезде ең үлкен дәлділікке қол жеткізуге болатындығын
көрсетеді.
Дефформациялар, тиісті ығысулардың дифференциялануымен есептеледі,
сондықтан деформациялар мен кернеулердің максималды дәлділігі элементтің
ортасында болады. 2.24-Сурет. таза иіліс жағдайына арналғандеформацияланған
бөлік көрсетілген.
Көріп тұрғанымыздай, теориялық және сандық шешімі, шектелген элементтің
ортаңғы жағында сәйкес келеді.
Элементтердің типі және саны есептеулердің дәлділігіне әсер етеді.
Осылайша, мысалы, шектелген элементтердің көп емес саны кезінде сызықтық
емес талдау жағдайында күшті есептегенде олардың саны есптеліп жатқан
күштің өлшеміне айтарлықтай әсер етеді. (2.25-Сурет). Алайда, элементтердің
саны үлкейгенде нәтижелер тұрақталады.

Шектелген-элементтік талдаудың екі әдісі бар: h-әдіс (ақырғы элемент
жағының ұзындығы) және р-әдіс (р-аппрокимицияланатын функияның полином
тәртібі). Шешімнің дәлділігін арттыру үшін h-әдісі элементтер санының
үлкейтілуін талап етеді. р-әдісіне сәйкес дәлділікті арттыру үшін
аппрокимицияланатын функцияның полином санын жоғарылату керек. Осылайша,
мысалы, (2.26,б-Сурет). көрсетілгендей анағұрлым жоғары тәртіпті элементтер
сызықтық элементтермен салыстырғанда нәтижелердің анағұрлым дәл нәтижелерін
береді (2.26,а-Сурет).

Сондай-ақ нәтижелердің дәлділігіне элементтер жақтарының ориентациясы
да әсер етеді. Иілетін консольді арқалық үшін, арқалық биіктігі бойынша
элементтер санының көбеюі нәтижелер дәлділігінің өсуін бермейді (2.26,в-
Сурет). Арқалық ұзындығының бойымен екінші қатардағы элементтердің өсуі
анағұрлым жақсы нәтижелер береді (2.26,г-Сурет).
Ақиқатты нәтижелерді алу үшін кернеулердің шоғырлану аймақтарында
элементтердің өлшемі кіші болуы тиіс. 2.27-Сурет орталық тесігі бар
созылатын жолақтың үзіндісі көрсетілген. Максималды кернеулер А-А қимасында
әрекет ететіндігі белгілі, сондықтан берілген қиманың маңайындағы
элементтердің торы жолақтың сол шекарасындағыға қарағанда қалынрақ болуы
тиіс.

2.7 Мысал – Сатылы стерженің созылуы

Сатылы стерженің өстік созылуының қарапайым мысалында ШЭӘ-нің негізгі
түсініктерін түсіндіреміз. Берілген мысал ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.