Мектеп математика курсында комбинаторика элементтерін ықтималдық есептерінде қолдану және оқыту әдістемесі


Мазмұны
Қосу және көбейту ережелері. Комбинациялардың тізімі.
Лексикографиялық рет . . .
Кіріспе
XX-ғасырдың екінші жартысында ғылым мен техниканың жаңа салаларының пайда болуы және олардың тез қарқынмен дамуына байланысты математиканың ықтималдықтар теориясы мен математикалық статистика элементтері тарауына деген сұраныс күрт артып отыр. Атап айтқанда, олар информация теориясы, қателер теориясы, физика және басқа жаратылыстану ғылым салаларында, сондай-ақ нарық заманында, күнделікті өмірде де тірек білім ретінде қолданылуда. Сондықтан да ықтималдық теориясы мен математикалық статистика элементтері тек қана жоғары немесе арнаулы оқу орындарында ғана емес, жалпы білім беретін орта мектептерде де оқытылуда.
Ықтималдықтар теориясы мен математикалық статистика элементтерін мектеп тәжірибесіне енгізу қазіргі қоғам талабына сай математикалық білім берудің мақсатынан, яғни оқушыларды әдіснамалық тұрғыда тәрбиелеуден, математика курсының дүниетанымдық көзқарасына бағдарлануынан, терең әрі негізделген пәнаралық байланыстарды құрудың мүмкіндіктерінен шығады. Бұл оқу материалдары адамның ақпаратты сауатты түсінуіне және талдауға білікті болуына, нақты тәуелділіктердің ықтималдық сипатын және оның формасын анықтауына, қарапайым есептеулерді жүргізе алуына өте қажет. Ықтималдық - статистикалық білімнің болмауы әлеуметтік, саяси, экономикалық ақпараттарды қабылдауға қиындық туғызады .
Комбинаторика - математика тарауларының бірі. Мұнда шекті жиын элементтерінің түрлі қосылыстары, басқаша айтқанда, әр қилы конфигурациялары қарастырылып, олардың сандары саналады және де есептеледі.
Теориялық зерттеу тұрғысынан алғанда комбинаторика алғаш рет ХVII ғасырдағы Паскаль, Ферма, Лейбниц және ХVIIІ ғасырдағы Я. Бернулли, Эйлер еңбектерінде қарастырылған. Ұлы математиктердің бұл шығармаларында комбинаторкалардың кездесуі бір жағынан алғанда тұрмыстың сан алуан мұқтаждарына байланысты болса, ал екінші жағынан алғанда, математиканың өз ішіндегі дамуларымен ұштасып жатыр.
Қазіргі кезде комбинаторика математика салаларының ішінде өте жедел дамып отырған бөлігіне айналды. Бұған себеп болып отырған бұл теорияның электрондық есептегіш машиналарға, информация мен ықтималдықтар теорияларына кеңінен қолданылуы. Дискреттік деп аталып жүрген математиканың өзінде де көп ықпалын тигізген, міне, осы қосылыстар теориясы. Шешуі: «нешеу», «неше тәсілмен» деген сұрауларға жауап беруді қажет ететін есептер комбинаторлық есептер делінеді. Мұндай есептерді шешумен айналысатын математика саласы комбинаторика деп аталады.
Кейінгі жылдары комбинаториканың практикада кең қолданыс табуына электрондық есептегіш техниканың дамуы шектеулі математика ролінің артуы, ыктималдықтар теориясы мен математикалық статистиканың практикалық маңызының күннен-күнге артуы негізгі себеп болып отыр.
Кейбір комбинаторикалық есептермен ежелгі грек математиктері де айналысқан. Дегенмен бұл саладағы маңызды нәтижелерді алгебра мен ықтималдықтар теориясының дамуына байланысты XVII және XVIII ғасыр математиктері ала бастаған. Алғашында ықтималдықтар теориясы, негізінен, құмар ойындардың (ойын сүйегін тастау, карта ойындары және т. с. с) мұқтаждығынан туындаған.
- ғасырдың екінші жартысында Паскаль мен Ферма арасындағы хат алысу кезінде ғалымдар құмар ойындарында кездесетін заңдылықтарды ғылыми тұрғыдан негіздеп бақты. Тарихшы ғалымдар ықтималдық теориясының пайда болуын осы хат алмасулардан бастау алады деп бағалайды. Бұл теорияның дамуына нидерланд математигі X. Гюйгенс (1629-1695), неміс ғалымы Г. В. Лейбниц (1646-1716), швейцар математигі Я. Бернулли (1654-1705) және өзгелер қомақты үлес қосты.
- ғасырда жаратылыстану және тұрмыс-тіршілік мұқтаждықтары (бақылау қателіктері теориясы, оқ ату теориясының есептері, статистика мәселелері және т. с. с. ) ықтималдықтар теориясының дамуын жаңа сатыға көтерді. Ықтималдықтар теориясында аналитикалық тәсілдерді қолдануда үлкен үлес қосқандар қатарында А. Муавр (1667-1754), П. С. Лаплас (1749-1827), К. Гаусс (1777-1855), С. Пуассон (1781-1840) сынды ғұлама математиктер болды. Ал ХІХ-ХХ ғасырларда ықтималдықтар теориясы мен математикалық статистиканың қалыптасып дамуына орыс математиктерінің қосқан үлесі зор.
Олардың қатарына П. Л. Чебышев (1821-1894), А. А. Марков (1856-1922), А. М. Ляпунов (1857-1918), С. Н. Бернштейн (1880-1968), А. Я. Хинчин (1894-1959), А. Н. Колмогоров (1903-1987) және өзгелерді қосуға болады. Мәселен, А. Н. Колмогоров ықтималдықтар теориясын аксиоматикалық жолмен тұрғызды .
Қазақстанда да ықтималдықтар теориясы мен математикалық статистика элементтері мәселесіне байланысты кең көлемде ғылыми-зерттеу жұмыстары жүргізілуде. Бұл іске көп жағдайда халық шаруашылығы бағытындағы жоғары оқу орындары оқытушы-профессорлары белсенділік көрсетуде. Аталған мәселе жайлы елімізде Қ. Б. Бектаев, Б. С. Жаңбырбаев, Р. Т. Келтенова, Н. Аханбаев, О. М. Мейрамқұлов, Қ. Ж. Серікбаева, Р. Ғ. Мейірманова, М. Ж. Бекбатшаев, Н. С. Саханов, К. Н. Бағысбаев, А. К. Қазешов, С. А. Нұрпейісов, Қ. Қаңлыбаев және т. б. ғалым -педагогтар ғылыми және педагогикалық жұмыстар жүргізді.
Орта мектептерде «Комбинаторика элементтері» тақырыбын оқыту 1973-1975 жылдарда факультативтік жұмыстарда жүзеге асты, ал 1975-76 оқу жылынан бастап, бұл тақырып жалпыға міндетті жаңа бағдарлама бойынша оқытылды. Кейінірек, 1980 жылдан математиканың бұл бөлімі мектеп бағдарламасынан алынып тасталды. Сөйтіп, ширек ғасырға жуық уақыт бойы орта мектепте де, педагогикалық жоғары оқу орындарында да комбинаторлық талдау есептерін шығару және оларды оқыту әдістемесі оқылмай қойды .
Қазіргі таңда комбинаторика, кездейсоқ жағдайлар алгебрасы және статистика теориясы элементтері бастамалары республикамыздағы бірқатар авторлардың алгебра оқулықтарынан, сондай-ақ, Қазақстанның жалпы орта білім беретін мектебінің 5-6 сыныптарына арналған математиканың жаңа стандарттық бағдарламаларының мазмұнынан нақты орын алды.
Орта мектептерде әзірге «Ықтималдықтар теориясының бастамасы» тақырыбын оқыту тәжірибесі жоқ, сондықтан, «Комбинаторика элементтері және оны ықтималдық теориясында қолдану» курсының сипаттамасы қызығу тудыру мүмкін.
Жұмыстың мақсаты: ықтималдықтар теориясы мен комбинаторика элементтерін теориялық тұрғыда негіздеп, орта мектепте оқыту әдістемесін жетілдіру.
Зерттеу нысаны: мектеп математика курсынадағы ықтималдықтар теориясы мен комбинаторика элементтерін оқыту.
Зерттеу пәні: мектеп математика курсынадағы комбинаторика және оны ықтималдықты есептеуде қолдануға оқыту әдістемесі.
Жұмыстың міндеттері: мектеп математика курсындағы комбинаторика және оны ықтималдықты есептеуде қолдану тақырыбының теориялық негіздерін, яғни, қосу және көбейту ережелерін, қайталанбайтын және қайталамалы таңдамалар үшін комбинаторика формулаларын ықтималдықты есептеуде қолдануды және тақырыптың қазіргі мектеп математика оқулықтарында баяндалуына талдауды жүзеге асыру.
1 Мектеп математика курсындағы комбинаторика және оны ықтималдықты есептеуде қолдану тақырыбының теориялық негіздері
- Комбинаторика ұғымы
Классикалық анықтамаға негізделген ықтималдықтарды
 есептеу А оқиғасының пайда болуына қолайлы, элементар оқиғалар саны
n
-ды табуға келіп тіреледі. Ықтималдықтар теориясында
m
мен
п
мәндері, ілгеріде көрсетілгендей оп-оңай анықтала бермейді. Бұларды табу ушін қайсыбір жиын элементтерін түрліше алу тәсілдерін қарастыруға тура келеді. Мәселен, жәшіктегі әріптер жиыны
а, b,
есептеу А оқиғасының пайда болуына қолайлы, элементар оқиғалар саны
n
-ды табуға келіп тіреледі. Ықтималдықтар теориясында
m
мен
п
мәндері, ілгеріде көрсетілгендей оп-оңай анықтала бермейді. Бұларды табу ушін қайсыбір жиын элементтерін түрліше алу тәсілдерін қарастыруға тура келеді. Мәселен, жәшіктегі әріптер жиыны
а, b,
 элементтерінен кұралған десек, онда бұл жиыннан әріптерді: 1) бір-бірден 3 тәсілмен аламыз
(а, b,
элементтерінен кұралған десек, онда бұл жиыннан әріптерді: 1) бір-бірден 3 тәсілмен аламыз
(а, b,
 ) ;
2) екі-екіден 6 тәсілмен аламыз (
ab, ba,
) ;
2) екі-екіден 6 тәсілмен аламыз (
ab, ba,
 ,
,
 ,
,
 ,
,
 ) ;
3) үш-үштен 6 тәсілмен аламыз
(ab
) ;
3) үш-үштен 6 тәсілмен аламыз
(ab
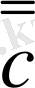 , a
, a
 b, ba
b, ba
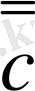 , b
, b
 a,
a,
 ab) .
ab) .
Мұндағы алынған әрiп тіркестерінің бір-бірінен айырмашылығы элементтерінде, не элементтерінің орналасу ретінде болып отыр. Мұндай тіркестер - жиын элементтерінің комбинациясы (қосылысы) болып, бірнеше реттелген жиындар жасайды. Мысалы, көрсетілген үш элементті жиыннан әрқайсысы екі элементтен 6 реттелген жиын алып отырмыз. Сондай-ақ 4 элементі {a, b, c, d} жиыннан әрбір екі элементтен тұратын 12 реттелген жиын алуға болады және т. с. с.
Комбинаториканы пайдаланып оқиға ықтималдығын анықтау таңдаманы жиыннан алу тәсіліне байланысты. Мұны түсіндіруді мысалдан бастайық.
1 - м ы с а л Елімізде автомашиналардың серияларын анықтау ісімен мемлекеттік автоинспекция шұғылданады. Олар екі, үш әріптен неше комбинация жасайтынын білуі керек. Бұл фактіні байланыс кызметкері де, кодылау мамандары да білуге тиіс. Сонымен, орыс алфавитіндегі 32 әріптен үш әріптен құралатын комбинацияны неше тәсілмен жасауға болады?
Ш е ш у і Бұл есепті шешу әріптер жиынынан алынатын үш әріп комбинациясына қойылатын талапқа байланысты. Түсінікті болу үшін бұл әріптердің әрбіреуін формасы бірдей жеке карточкаларға жазайық. Сөйтіп, оларды топтастырайық, яғни бір колода етейік. Сонда колодадағы карточкалар жиын болады. Әріптерді колодадан екі түрлі жолмен таңдап алуға болады.
Бірінші тәсіл (қайталанбайтын таңдама) . Бірінші алынатын әріп колодадағы 32 әріптің бірі болады, яғни оны 32 тәсілмен алуға болады. Ал, екінші әріп колодада қалған 31 әріптен алынады. Сонда шығатын әр түрлі екі әріпті комбинациялар саны 32·31=992 болады. Бұл екі әріпті тіркестердің әрқайсысы үшінші алынатын әріппен тіркесіп үш әріпті тіркес құрайды. Сонда олар 32·31·30 = 29760 тәсілмен алынады. Бұл жағдайда әрбір үш әріпті тіркестегі әріптер әр түрлі болып кездеседі.
Екінші тәсіл (қайталанатын таңдама) . Бірінші алынған әріп таңбасы белгіленген соң, ол колодаға қайыра салынады. Сонда екінші алынатын әріп те колодадағы 32 әріптің бірі болады. Олай болса, екі әріпті тіркестерді 32·32 = 32 2 = 1024 тәсілмен алуға болады. Осы сияқты үш әріпті тіркестер
32·32·32 = 32 3 = 32768
тәсілмен жасалады. Бұл жағдайда үш әріпті тіркестердің жасалуына ешқандай шек қойылмайды, яғни мұнда әрбір әріп бір тіркестердің ішінде екі рет, үш рет кайталанып келуі мүмкін.
Сонымен, 32 әріптен үш-үштен алу таңдама болып табылады. Бірінші жолы колодадан қай әріп алынатыны белгілегеннен кейін, колодаға ол қайта салынған жоқ. Сондықтан мұндай таңдаманы қайталанбайтын таңдама деп атаймыз. Екінші жолы колодадан алынған әріп белгіленіп алынғаннан кейін, ол қайтадан колодаға салынады. Сонда екінші әріп колодадағы 32 әріптің ішінен алынады. Үшінші әріпті алғанда да өзгермейді. Сондықтан бұлай таңдауды қайталанатын таңдама деп атайды. Ал, элементтері алынып отырған жиын, яғни 32 әріп жиыны бас жиын болады. Әдетте, бас жиындағы әріптеp сол жиын элементтері болады.
Бұл мысалдардың екеуінде де комбинация санын анықтағанда көбейтудің мынадай ережесін пайдаланғандығымызды байқау қиын емес.
Көбейту ережесі Егер А жиыны

элементтерінен, яғни
m
элементтен, ал
В
жиыны
 элементтерінен, яғни
k
элементтен құралатын болса (бұл екі жиын бір жиыннан алынуы да мүмкін), онда олардың әрқайсысынан бір-бір элементтен алынған әр түрлі
элементтерінен, яғни
k
элементтен құралатын болса (бұл екі жиын бір жиыннан алынуы да мүмкін), онда олардың әрқайсысынан бір-бір элементтен алынған әр түрлі
 комбинациялары саны
mk
болады
комбинациялары саны
mk
болады
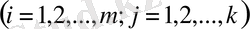 .
.
Шынында да, бұларды
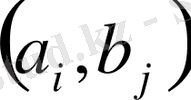 түрінде
m
горизонталь және
k
вертикаль жолдардан тұратын мына таблицаға орналастыруға болады.
түрінде
m
горизонталь және
k
вертикаль жолдардан тұратын мына таблицаға орналастыруға болады.
1-кесте
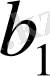
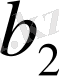




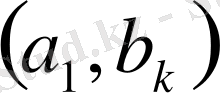

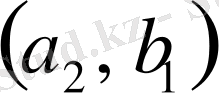

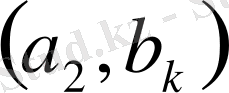


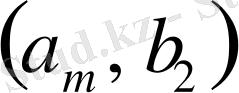
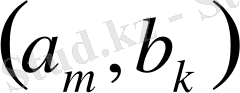
Бұл таблицадағы әрбір
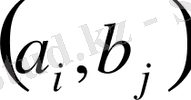 тек бір реттен ғана кездеседі. Олардың барлық саны -
mk
. Бұл ереже жиын саны екіден артық болғанда да орындалады. Мысалы, элементтер саны сәйкес
т, k
,
h
болатын үш жиын
тек бір реттен ғана кездеседі. Олардың барлық саны -
mk
. Бұл ереже жиын саны екіден артық болғанда да орындалады. Мысалы, элементтер саны сәйкес
т, k
,
h
болатын үш жиын
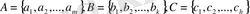 берілсін. Әр жиыннан тек бір элементтен ғана алынған әр түрлі
берілсін. Әр жиыннан тек бір элементтен ғана алынған әр түрлі
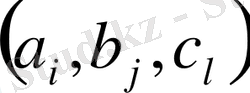 үш элемент комбинациясын жасауға болады, мұндағы
үш элемент комбинациясын жасауға болады, мұндағы
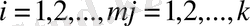 және
және
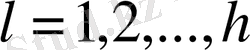 .
Олардың саны
т, k, h
болады, өйткені
А
және В жиындарынан алынған әрбір
.
Олардың саны
т, k, h
болады, өйткені
А
және В жиындарынан алынған әрбір
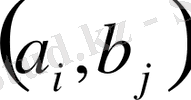 пары үшінші жиынның әрбір элементімен комбинацияланады. Бұл комбинациялар саны, әрине
(mk) h = mkh
санына тең. Енді комбинаторика үғымын ықтималдықтар теориясының есептерін шешуге қолданамыз. Ол үшін бірнеше формулаларды қорытудың қажеттігі туады. Бұл формулалар екі түрлі жағдайда қарастырылады. Біріншісі қайталанбайтын таңдама үшін болса, екіншісі қайталанатын таңдама үшін болады.
пары үшінші жиынның әрбір элементімен комбинацияланады. Бұл комбинациялар саны, әрине
(mk) h = mkh
санына тең. Енді комбинаторика үғымын ықтималдықтар теориясының есептерін шешуге қолданамыз. Ол үшін бірнеше формулаларды қорытудың қажеттігі туады. Бұл формулалар екі түрлі жағдайда қарастырылады. Біріншісі қайталанбайтын таңдама үшін болса, екіншісі қайталанатын таңдама үшін болады.
Қайталанбайтын таңдама үшін комбинаторика формулалары 9-класс математикасында қорытылған. Бұл формулаларды және оларға тиісті есептерді шешуді ұсына отырып, ықтималдықтарды есептеуге арналған мысалдарды келтіреміз.
1. 2 Қайталанбайтын таңдамалар үшін комбинаторика формулалары
О р н а л а с т ы р у л а р
Алдыңғы 1-мысалдың бірінші шешуінде орыс алфавитінен алынған үш әріп комбинациялары саны 32·З1·30=29760 еді. Алфавит N әріптен тұрса, онда әрқайсысы үш әріптен тұратын комбинациялар саны N(N-1) (N-2) болар еді. Ал енді 3 әріп орнына әрқайсысы k әріптен комбинациялар құрсақ, олар N(N-1) (N-2) …(N-(k-1) ) тәсілімен орындалады. Бұл өрнек
N элементтен әрқайсысы k-дан жасалған орналастырулар саны
делінеді. Бұл орналастырулардың әрқайсысына
N
элементтің ішінен
k
элемент еніп, олардың айырмашылықтары не элементтерінде, не элементтерінің орналасу ретінде болады. Мұны
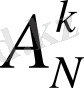 символымен белгілейік. Сонда
символымен белгілейік. Сонда
 (1)
(1)
Өрнекті ықшамдаған қолайлы. Ол үшін (1) өрнегінің оң жағын 1, 2, 3, . . . , (N-k) сандарына көбейтеміз және бөлеміз. Сонда
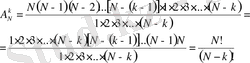
яғни
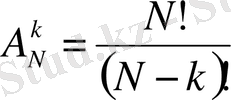 (2)
(2)
Мұнда
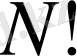 -
эн факториал
деп оқылады, ол 1-ден
-
эн факториал
деп оқылады, ол 1-ден
 -ге дейінгі натурал сандардың көбейтіндісіне тең, яғни
-ге дейінгі натурал сандардың көбейтіндісіне тең, яғни
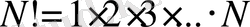 (3)
(3)
2 - м ы с а л Е, К, М, Н, Т, Ш, Ы әріптері бірдей карточкаларға жазылып, бір колодаға салынған. Оларды әбден араластырып бір-бірден төрт карточка аламыз. Сонда: а) 7 әріптен төрт-төрттен нешe тәсілмен алуға болады: ә) алынған 4 әріпті қатарынан тізіп қойғанда «КЕНТ» сөзінің пайда болу ықтималдығын есептеу керек.
Ш е ш у і а) Колодадан алынған бірінші карточка сондағы 7 карточканың бірі, яғни бірінші карточканы 7 тәсілмен алуға болады. Екі карточканы 7·6 тәсілмен алуға болады, өйткені бірінші карточка алынғаннан кейін екіншісін колодадан қалған 6 карточканың ішінен алынады. Оның үстіне, әрбір бірінші әріп әрбір екінші әріппен 7·6 рет комбинацияланады. Осы сияқты, 3 әріп алынатын комбинация 7·6·5 тәсілмен, 4 әріптен алынатын комбинация 7·6·5·4 тәсілмен құралады. Есеп шарты бойынша
N =7, k = 4,
енді (1) формуласын пайдалансақ:
А
7
=7·6·5·4 = 840 немесе (2) формуласы бойынша

ә) Алдымен n-ді анықтайық. n = 840 болатынын көрдік. Бұл барлық тең мүмкіндікті элементар оқиғалар саны. Енді аталған сөздің пайда болуына қолайлы элементар оқиғалар саны m-ді табамыз. 4 әріпті тіркестер ішіндегі бізге қолайлысы тек бірінші орында «К», екінші орында «Е», үшінші орында «Н», ақырында, төртінші орында «Т» әрпі тұратын «КЕНТ» сөзі ғана болмақ. Бұл сөз тек бір-ақ рет кездеседі. Сондықтан іздеген ықтималдық мынаған тең:

Алмастырулар N элементтен N -нен алынған орналастыруларды алмастырулар деп атайды. Алмастырулардың бір-бірінен айырмашылығы тек элементтерінің орналасу ретінде ғана, өйткені әрбір алмастырудағы элементтердің саны бірдей. Сонда (1) формуласында, k = N десек,
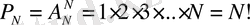 (4)
(4)
3 - м ы с а л 2-мысалда келтірілген Е, К, М, Н, Т, Ш, Ы әріптерінен: а) неше алмастырулар жасауға болады? ә) карточкаларды қатарынан қойғанда «Шымкент» сөзінің шығу ықтималдығын анықтау керек.
Ш е ш у і а) Айырмашылығы тек элементтерінің орналасу ретінде ғана болатын 7! алмастырулар жасауға болады.
ә) Бұл алмастырулардың әрқайсысының шығу мүмкіндігі бірдей. Сонда тең мүмкіндікті барлық элементар оқиғалар саны п=7! болады. Бұлардың ішінде «Шымкент» сөзінің шығу мүмкіндігі біреу-ақ демек, оның ықтималдығы
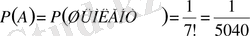
Т е р у л е р N элементтен әрқайсысы k- дан алынған орналастыруларды бір-бірінен айырмашылығы не элементтерінде, не элементтерінің орналасу ретінде болатын комбинациялар деп қарастырдық. Орналастырулардың айырмашылығы тек элементтерінің орналасу ретінде ғана болатын дербес түрін алмастырулар дедік. Сондай-ақ айырмашылығы кемінде бір элементінде болатын орналастырулардың дербес түрі теру деп аталады.
Сонымен, N элементтен әрқайсысы
k
элементтен алынған терулер санын
 деп белгілесек,
k
элементтен жасалған алмастыруды
P
k
десек, онда сол
N
элементтен
k
-дан алынған орналастыруда
(A
деп белгілесек,
k
элементтен жасалған алмастыруды
P
k
десек, онда сол
N
элементтен
k
-дан алынған орналастыруда
(A
 )
алмастырудың да, терудің де қасиеттері қамтылғандықтан
)
алмастырудың да, терудің де қасиеттері қамтылғандықтан
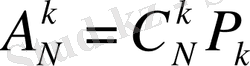 (5)
(5)
болады.
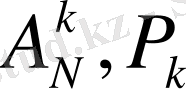 мәндерін (5) формулаға қойсақ.
мәндерін (5) формулаға қойсақ.
 (6)
(6)
Бұл өрнектің оң жақ бөлігіндегі бөлшектің алымын да, бөлімін де 1·2·3· . . . · (N - k) санына көбейтсек,
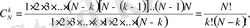
яғни
 (7)
(7)
формуласы шығады. Бұл формуланы мұнан былай жиі қолданамыз. (6) формуласы
N=0
және k = 0 мәндерінде де дұрыс болуы үшін 0!=1 деу керек.
N
мен
k
мәндері үлкен болғанда
 мәнін ( 6) формуласымен есептеу аса қиынға соғады. Сондықтан факториалдар логарифмдерін пайдалану қолайлы. Осы себепті 100 факториалға дейінгі сандар логарифмдерінің кестесін пайдалану керек.
N!
-ды есептеудің жуық формуласында пайдаланады. Бұған көбінесе анализден белгілі мына Стерлинг формуласы алынады.
мәнін ( 6) формуласымен есептеу аса қиынға соғады. Сондықтан факториалдар логарифмдерін пайдалану қолайлы. Осы себепті 100 факториалға дейінгі сандар логарифмдерінің кестесін пайдалану керек.
N!
-ды есептеудің жуық формуласында пайдаланады. Бұған көбінесе анализден белгілі мына Стерлинг формуласы алынады.
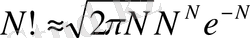 (8)
(8)
Есеп шығарғанда әдетте мұның екі жағын логарифмдейді.
Терудің негізгі екі қасиетін келтірейік. 1° - қ а с и е т.
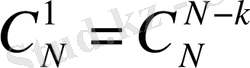 (9)
(9)
Мұны дәлелдеу үшін (6) формуладағы k орнына N-k қоямыз. Сонда
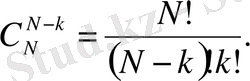 (10)
(10)
екені шығады. (6) және (9) өрнектерінің оң жақ бөліктері тең болғандықтан бұлардың сол жақ бөліктері де тең болады, яғни
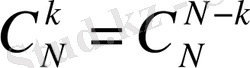
2° - қ а с и е т
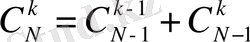 (11)
(11)
Мұны дәлелдеу үшін
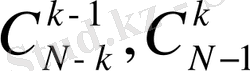 орындарына олардың (7) формуласындағы мәндерін қойып жазсақ,
орындарына олардың (7) формуласындағы мәндерін қойып жазсақ,

Терудің екінші қасиетін пайдаланып Паскаль үшбұрышы деп аталатын төмендегі схеманы келтіру қолайлы.
Паскаль үшбұрьшы
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
Бұл үшбұрыштың құрылысымен танысқанда мынадай ережені байқау қиын емес: төменгі қатардағы әрбір сан (екі шеткісін қоспағанда) оның үстіңгі қатарындағы сол цифрдың үстіндегі (оң жақ және сол жақ) екі санның қосындысына тең, яғни
С
N
мәні N-қатар үстіндегі
(N-
1) -қатардағы теру мәндеріне сәйкес (11) формуласы негізінде табылған. Сонымен,
 мәні N-қатар мен
k-
диагональдың қиылысуындағы санға тең. Мысалы
N=8, k = 3
болғанда
мәні N-қатар мен
k-
диагональдың қиылысуындағы санға тең. Мысалы
N=8, k = 3
болғанда
 мәні 8-қатармен k = 3-ке сәйкес диагональдағы 56 санына тең.
мәні 8-қатармен k = 3-ке сәйкес диагональдағы 56 санына тең.
Әрбір қатардағы сандардың қосындысы
2
N
санына тең. Мысалы, N=3 болғада 1+3+3+1=8=2
3
,
N=7
болғанда 1+7+21+35+35+21+7+1=128=2
7
. Бұл (1+1)
7
биномын Ньютон формуласы бойынша жіктелгенге тең. Шынында да, Ньютон формуласы бойынша
(а+bх)
п
биномын жіктесек,
 десек, онда
десек, онда
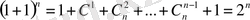
4 - м ы с ал N=100, k = 50 болғанда
 мәні неге тең?
мәні неге тең?
Ш е ш у і
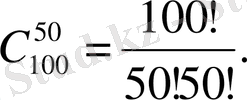 Енді мұның екі жағын да логарифмдейміз, сонда
Енді мұның екі жағын да логарифмдейміз, сонда
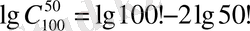 болады. Логарифмдер таблицасынан lg100! = 157, 9700, lg50!=64, 4832. Демек,
болады. Логарифмдер таблицасынан lg100! = 157, 9700, lg50!=64, 4832. Демек,
 29, 0038. Бұдан
29, 0038. Бұдан
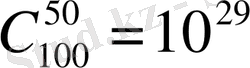 өте үлкен сан екені шығады. Ал ықтималдықтарды есептегенде көп жағдайда N мен
k
үлкен болып келгенімен, факториалдар логарифмдерін пайдаланып есептеу жеңілге соғады.
өте үлкен сан екені шығады. Ал ықтималдықтарды есептегенде көп жағдайда N мен
k
үлкен болып келгенімен, факториалдар логарифмдерін пайдаланып есептеу жеңілге соғады.
Енді
 -ді Стирлинг формуласымен есептейік. Сонда
-ді Стирлинг формуласымен есептейік. Сонда
100!=
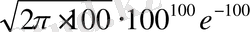
немесе
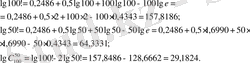
Сонымен бұл формуламен есептеу дәлдігі факториалдың нақты шын мәніне мейлінше жуык екенін байқаймыз.
5-мыса л Жәшікте бірдей N нәрсе бар. Олардың, М нәрсесі жарамды да N-M=D нәрсесі жарамсыз. Жәшіктен кез келген s нәрседен тұратын таңдама алынды, мұның т-і жарамды, d-ci жарамсыз нәрсе болу ықтималдығын анықтау керек.
Ш е ш у і
N
нәрседен s-тен таңдаманы
 тәсілмен алуға болады. Бұл нәтижелер - барлық тең мүмкіндікті элементар оқиғалар. Қолайлы элементар оқиғалар санын анықтайық. Жарамдыны тек жарамды нәрселерден
тәсілмен алуға болады. Бұл нәтижелер - барлық тең мүмкіндікті элементар оқиғалар. Қолайлы элементар оқиғалар санын анықтайық. Жарамдыны тек жарамды нәрселерден
 тәсілмен аламыз, ал жарамсызды тек жарамсыз нәрселерден
тәсілмен аламыз, ал жарамсызды тек жарамсыз нәрселерден
 немесе
немесе
 тәсілмен аламыз. Алынған таңдамада жарамды да, жарамсыз да нәрселер болуы мүмкін. Олардың шығу комбинациясы
тәсілмен аламыз. Алынған таңдамада жарамды да, жарамсыз да нәрселер болуы мүмкін. Олардың шығу комбинациясы
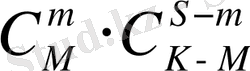 -ге тең. Демек, мұның ықтималдығы
-ге тең. Демек, мұның ықтималдығы
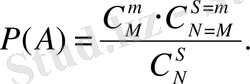
6 - м ы с а л Преферанс ойынында 32 картаны он-оннан үш адамға таратып, екеуін төңкеріп қояды. Осы төңкеріп қойылған карталардың: а) екеуінің де тұз болу ықтималдығы неге тең? ә) біреуі тұз біреуі дама болу ықтималдығы неге тең?
Ш е ш у і 32 картадан 2 картаны
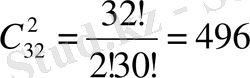
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz