Тор құрудың әдістері

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 48 бет
Таңдаулыға:

Жоспар
Кіріспе 3
1 Бір айнымалы функцияларды интерполяциялау 5
1.1 Бір айнымалы функцияны кубтық сплайнның көмегімен интерполяциялау 5
1.2 Тегістеу арқылы құрама-кубтық интерполяциялау 8
1.3 Тегіс толықтыру 11
1.4 Екі немесе бірнеше айнымалылар функциясын интерполяциялау 12
1.5 Көп айнымалылар функциясының r – тегіс жуықтауы 15
2 Есептік торлар құрудың әдістері 17
2.1 Алгебралық әдістер. Дифференциалдық теңдеулерді 19
шешуге негізделген әдістер 19
2.2 Бір байланысты аймақ 26
2.3 Көп байланысты аймақ 30
2.4 Көпбайланысты аймақ үшін эквиүлестіру әдісі 32
2.5 Дербес туындының теңдеуін шешу негізінде құрылатын торлар 35
2.6 Интегралдау аймағында тор құрудың әдістері 37
2.7 Бейімді торлар. Тор құрудың әдістері 39
3 Торларды құру 49
3.1 Кездейсоқ қисық сызықты координаталарда, ортогональ қисық сызықты тор
құру 51
Қорытынды 60

Кіріспе

Физикалық процесстерді математикалық моделдегенде, шекаралары қисық
сызықты болатын физикалық аймақ жиі кездеседі. Мұндай аймақтарда бейімді
қисық сызықты тор құрған, санау уақытын қысқартуға, бағдарламалауды
автоматтандыруға мүмкіндік береді. Соңғы жылдары қисық сызықты тор құру
әдістері және ерікті қисық сызықты координаталарда гидродинамика есептерін
сандық шешу жылдам дамыды. Бұл мәселе С.К. Годунова, Г.П.
Прокопова [1], Н.Н. Яненко, В.Д. Лисейкина, Н.Т. Данаева [2-3], П.Н.
Вабищевича [4], J.F. Thompson, Z.U.A. Warsi, C.W. Mastin [5] бұл жұмыстарда
негізінен қисық сызықты және динамикалық бейімді торларды, бір байланысты,
екі өлшемді және үш өлшемді аймақтарда құру қарастырылған.
Торда берілген функцияны барлық облыстарын үздіксіз функциялармен
толықтыру кезінде интерполяция мәселесі туындап отырады. Бұл жайлы
Н.С. Бахвалов, А.А. Самарский, Н.Н. Калиткин, Г.И. Марчук,
А.Л. Самарскийдің жұмыстарында қарастырылған. Интерполяция
есебі жоба-конструкторлық жұмысын автоматтандыру жүйесінде маңызды, негізгі
бөлігі болып табылады. Бұл интерполяциялау мәселесі математикалық
әдебиеттерінде классикалық әдістерде толығымен баяндалғандықтан жаңадан
мәселе болып табылмайды. Соңғы он жылдықта интерполяция теориясының бағыты
сплайн интерполяцияны қолдану болып табылады.
Сплайн интерполяция қисық сызықты торлы функцияны тегіс толықтыруды
тұрғызуда ең жақсы амал. Сплайнның тиімділігі оның арнайы экстремальді
қасиетімен байланысты. Сплайндық жуықтау барлық ғылым мен техника ортасында
кеңірек қолданылып келеді.
Жалпы дискретті нүктелер жиынында берілген шаманы интерполяциялау
мәселесі варияциялы-айырымдық сұлбаны және айырымдық есептердің шешімін
үзіліссіз көрсетілімін құрумен тығыз байланысты. Біз есептерді басқа
тұрғыда қарастырамыз. (a,b) кесіндісінің n+1 нүктесінде (интерполяция
түйінінде) 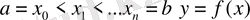функцияның 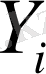-ң мәні берілген.
1.
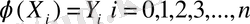
2. 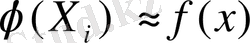барлық қалған мәндер үшін
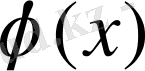қосалқы функцияны (интерполяцияланған функцияны) жинақтау керек. Басты
сұрақ мынада – интерполяцияны қалай таңдау керек және 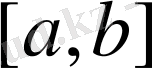кесіндісінде
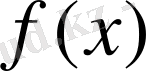функцияның жуықтау дәлдігін қалай бағалау керек.
Сандық әдісте ең негізгі есептердің бірі – функцияны интерполяциялау
болып табылады. Интерполяция кесіндісінде барлық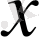-тің мәні
үшін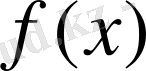функциясын қалпына келтіруден тұрады, егер кесіндінің нүктесінде
ақырғы санының мәні белгілі болса. Бұл мәндер қандай да бір жасалған
тәжірибе бақылауында (өлшемінде) немесе есептеу нәтижесінде табылуы мүмкін.

кесіндісіне 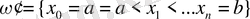тор берілсін делік, оның тоғысында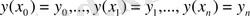тең
болатын 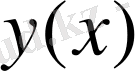функциясының мәні берілген болсын. Бұл жерде жұмыстың
өзектілігі – тор түйіндерінде 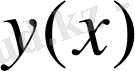функциясына сәйкес келетін
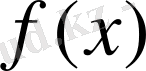функциясын интерполяциялау, яғни интерполяцияны тұргызуды қажет етеді.
Жоғарыда айтып кеткендей, соңғы жылдары интерполяция жаңа әдістермен
байи түсті. Олардың бірі сплайндық интерполяция.
Негізгі мақсаты – қарастырылатын қисық сызықты облыстың шекарасынын
интерполяциялауда үзіліссіздігін қамтамасыз ете отырып, интерполяциялаудың
бағдарламасын құру.
Жұмыстың міндеттері:
- Бір айнымалы функцияларды интерполяциялау.
- Есептік тор құру әдістері.
- Тор салудың әдістерін қарастыру.
- Бір байланысты аймақта тор құру.
- Кездейсоқ қисық сызықты координаталарда, ортогональ қисық сызықты тор
құру.
- Қисық сызықты облыстың аймағын интерполяциялау.
Жұмыстың құрылымында: кіріспе, негізгі бөлім, қорытынды бөлім,
әдебиеттер тізімі, формулалар, суреттер қолданылады.

1 Бір айнымалы функцияларды интерполяциялау

1.1 Бір айнымалы функцияны кубтық сплайнның көмегімен интерполяциялау

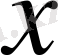нақты осінің 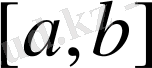кесіндісінде 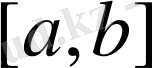анықталған, түйінінде
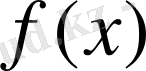функциясының 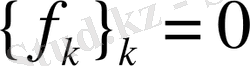мәні берілген 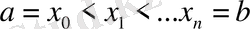тор берілсін делік. Онда құрама-
кубтық интерполяция есебі келесі түрдегідей қойылады. [a,b] кесіндісінде
келесі талаптарды қанағаттандыратындай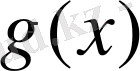функциясын табу керек:
1. С² класына жатады, яғни екінші ретке дейін өзінің үздіксіз
туындыларымен бірге.
2. Әрбір кесіндіде кубтық көпмүшелік түрінде

(1.1.1)
болып табылады.
3. {xn}k=0 тордың түйініде теңдік орындалады.

(1.1.2)
4. g´´(x) шекаралық шартты қанағаттандырады g´´(a)= g´´(b)=0
(1.1.3)
Алдағы уақытта анықталған 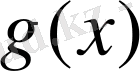функциясының жалғыз экстремальді қасиетін
орнатқан кезде біз таңдап отырған интерполяцияның артықшылығы анықталады.
Интерполяцияланған құрама-кубтық 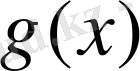функциясын табуға берілген
есептің жалғыз шешімі бар екенін көрсетейік. Ол үшін жоғарыда көрсетілген
(1)-(4) талаптарды қолданамыз.
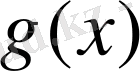функцияның екінші ретті туындысы әрбір тордың 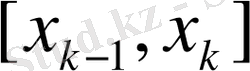кесіндісінде
үздіксіз және сызықты болғандықтан, біз 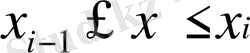болғанда

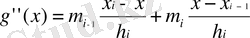(1.1.4)
деп жазамыз. Мұнда .
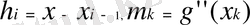Теңдіктің екі бөлігін де екі рет интегралдасақ
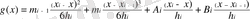(1.1.5)

аламыз, мұнда және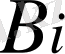интегралдау тұрақтылары. Олар g(xi-1)=fi-1
шартынан шығады. (1.1.5) x =xi және x =xi-1 қоя отырып,
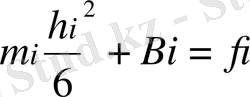
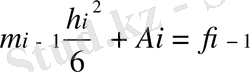аламыз.
Қорытындылай келе
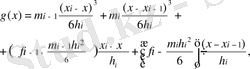(1.1.6)
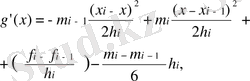(1.1.7)

(1.1.7) формуласынан туындының x1,x2,...,xn-1 нүктелерінде бір жақты
шектеулерді табамыз.

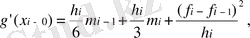
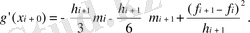
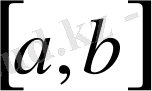g´´(x) және g´(x) функциясы үздіксіз шартына сәйкес
нүктесіндегі g´(x) үздіксіз шартынан n-1 теңдігін аламыз.

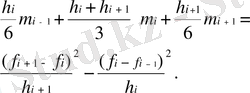(1.1.8)

(1.1.3) шартынан осы теңдікті толықтыра отырып, белгісіз табу үшін
сызықты алгебралық жүйені аламыз.
Am=Hf

(1.1.9)
А квадратты матрица

(1.1.10)

түрде болады. m және f векторлары және H тікбұрышты матрицасы былай
болады:
,

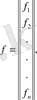
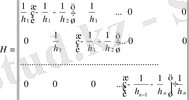(1.1.11)

А матрицасы қатаң диагональдық басымдылықпен симметриялы. Гершгоринның
өзіндік мәнін таратпаушылық жайлы теоремасы бойынша айқындалған және де
ерекше емес. Сонымен, m1,m2,...,mn-1 коэффициенттері (1.1.9) жүйесінен бір
мәнінде анықталады. Сондықтан, g(x) сплайн функциясы да (1.1.1- 1.1.6)
формуласымен бір мәнде қалпына келтіріледі және g(x) құрама-кубтық
функцияны табудағы есеп жалғыз шешімнен тұрады.
Құрама-кубтық функциясы сплайн-интерполяциясының жоғары тиімділігін
қамтамасыз ететіндіктен өте маңызды қасиеттерді иеленеді. Атап айтқанда,
екінші ретті туындының квадратты қосындылаулары бар функциядан тұратын
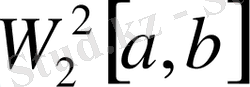класын [a,b] кесіндісінде қарастырайық. Есепті 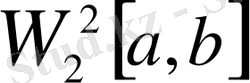класында
функционалды минимизациялайтын ізделінді интерполяцияланған функцияға
қоямыз:

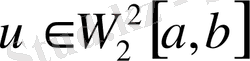, u(xk)=fk , k=0,1,...,n
(1.1.12)

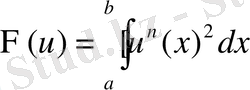(1.1.13)
Мұндай функционалдың минимумы жәнегі біз салған g(x) құрама-кубтық сплайн-
функциясына жететіндігі анықталады. Шынымен де мына шаманы қарастырайық:

(1.1.14) g мен функцияларының қасиеттерін қолдана отырып және
бөлшек бойынша интегралдай отырып

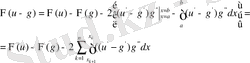
Бірақ 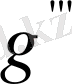= Ck=const [xk-1,xk] кесіндісінде болғандықтан

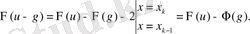
Осыдан және (1.1.14) формуласынан кез келген 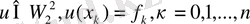функциясы үшін
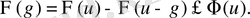
(1.1.12), (1.1.13) формулаларына негізделе отырып, құрама-кубтық сплайн-
функциясына: тор түйінінен берілген мәнді қабылдайтын, 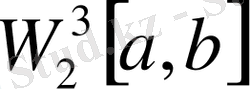классынан және
(1.1.13) функционалын минимилизациялайтын функция деп эквиваленттік
анықтама беруге болады.
Кубтық сплайн-функциясы жақсы жуықтау қасиетін иеленеді. Егер
иетерполяцияланатын функция 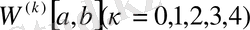класына жататын болса, онда
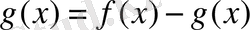функция қателігі үшін

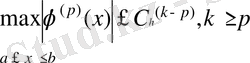(1.1.16)

теңсіздігі болғаны жөн, мұндағы - 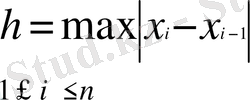торына тәуелсіз теріс емес
тұрақты.

1.2 Тегістеу арқылы құрама-кубтық интерполяциялау

Бұл бөлімде біз тағы да торда анықталған 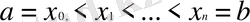тегіс толықтыру жайлы
есебін қарастырамыз. Бірақ та 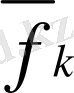функцияның мәні тор түйінінде біршама
қателіктерге ие болады. Бұл кезде түйіндіде, дәлдікте берілген мәнмен
сәйкес келетін интерполяциянған функцияны салудың қажеті жоқ. Оның үстінде
интерполяцияланғаннан гөрі берілген мәнге жақынырақ өтетін функцияны салу
керек болады. Ал мұндай функциялар енді интерполяциялық емес, тегістелген
деп аталады.
Ізделінді 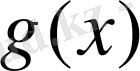тегістелген функциясы 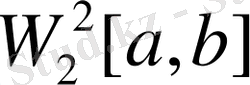классында

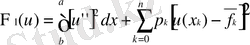(1.2.1)

функционалын минимизациялауын талап етеміз, мұнда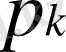- кейбір оң сандар.
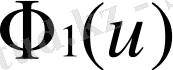функционалында берілген қисық мәннің жанынан және бүгу функциясының
минимал шартынан өтетін интерполяциялық шарттар араласқан. зілдеме
коэффициенті көп болған сайын, функционалға интерполяциялық шарттарды
қосады, берілген мәнге жақын тегістеу функциясы өтеді.
(1.2.1) вариациялық есептердің шешімі кубтық сплайн болып табылатынын
қарастырайық, яғни алдыңғы бөлімшедегі талаптарды қанағаттандыратын
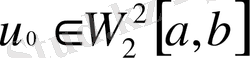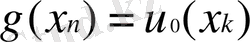
функция. - есептің шешімі болсын. 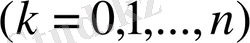болатын 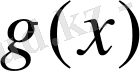сплайнын
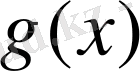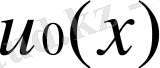тұрғызамыз. (1.2.1) екінші қосылғыш пен функциясы үшін бірдей
болғандықтан

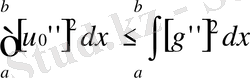(1.2.2)

Бірақ, алдыңғы бөлімшеде көрсетілгендей, 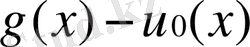интерполяциялау кезінде
минимум 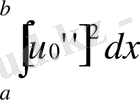өрнегін беретін жалғыз функция. Сондықтан .
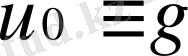Сонымен 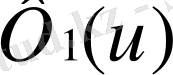функционалының минимумын кубтық сплайн классында табу
жеткілікті. 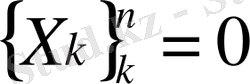түйінінде қабылдайтын кубтық сплайн бір мәнде оның
мәнінде жиынмен анықталғандықтан, 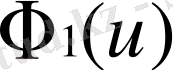минимизациясы
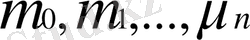айнымалылардан функция минимумын табуға апарады.
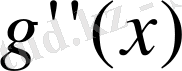- құрама-кубтық функция екенін білеміз, сонымен ,
, ,

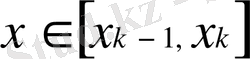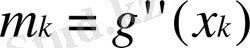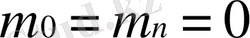
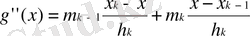(1.2.3)
Болғандықтан

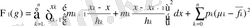(1.2.4)

(1.2.4) формулада интегралды туындай келе

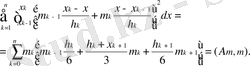(1.2.5)
аламыз.
Мұнда 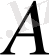- белгілі матрица. Сонымен

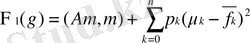(1.2.6)
1.1.9 нәтижесінде 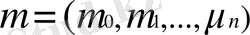арқылы сызықтық көрсетіледі, сондықтан -
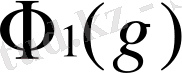да 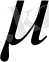- ден анықталатын оң форм болуы мүжетті шарты болып табылатын
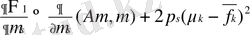оның экстремумы болып тек қана минимум болуы мүмкін. Бірақ
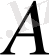матрицасы 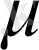- ге тәуелді емес.
Сондықтан (1.1.9) байланысты

(1.2.7)

Мұнда (1.1.11) формуласымен анықталады. Осыдан минимум шарты
векторлық формада мынандай түрде 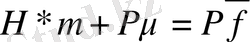(1.2.7) шығады, мұнда ,
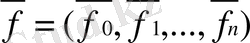ал 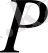- диагональді матрица:

(1.2.8)

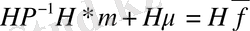1.2.7-нің сол жағын көбейте отырып, , немесе
(1.1.9) ескере отырып, түпкілікті

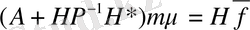(1.2.9)
аламыз.
(1.2.9) жүйенің матрицасы бес диагональды, симметриялы және дұрыс
анықталған. (1.2.9) жүйесін мысалы, Гаусс әдісімен шығаруға болады. Осыдан
кейін m векторы анықталғандықтан, 1.2.7 формуласынан жалғасатын
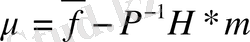формуласымен тегістеу сплайнның торлы мәнінің векторын іздеу қажет. Одан
1.1.6 формуласы бойынша 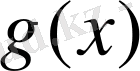сплайны қалыптасады.
Кубтық сплайнмен тегістеу – тегістеудің жалғыз ғана әдісі емес.

1.3 Тегіс толықтыру

Енді торлы функцияның тегіс толықтырудың басқа әдісін айтамыз, оның
сплайн-функция әдістер теориясынан бірнеше айырмашылығы бар, сонымен
алгоритмдік көзқараста өте тиімді. 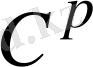тұрақты тегістеу классының
интерполяциялық функциясын құру процессін өте қысқаша сипаттайық. Түйінде
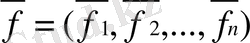функцияларының мәні белгілі 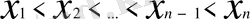- кейбір бекітілген тор болсын.
жетерліктей үлкен деп болжайық. бүтін санын белгілейік. Алдымен,
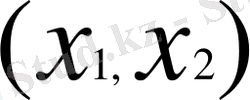тор кесінді де 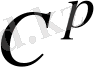тегістеу классының интерполяциялық функциясын
құрайық. Тор түйінінде берілген 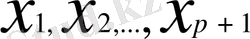мәнімен сәйкес дәрежесінен жоғары
емес келетін Лагранж көпмүшелігін 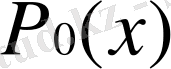арқылы белгілейміз, ал 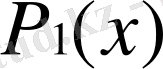арқылы
түйінде берілген 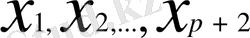мәндерді қабылдайтын дәрежесінен жоғары емес
Лагранж көпмүшелігін белгілейміз. Ары қарай мына шартты қанағаттандыратын

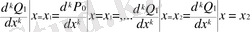
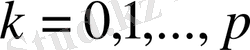(1.3.1)
Қанағаттандыратын, 2p+1 дәрежесінен жоғары емес 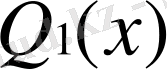көпмүшелігін
тұрғызамыз. Мұндай 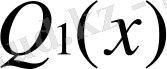көпмүшелігі бар және шартта бірмәнде анықталғаны
айқын.
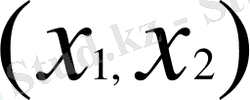кесіндіде 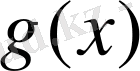интерполяциялық функция 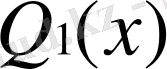тең болсын.Сурет
ретінде p=1 жағдайын қарастырумен шектелеміз. Онда 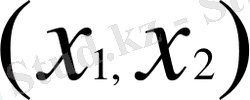кесіндіде 3-ші
дәрежелі 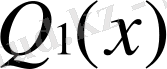көпмүшелігін:

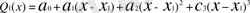
түрде жазылады. Олардың коэффициенттері

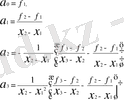(1.3.2)
формуласы бойынша есептеледі.
Егер бастапқы үшін санауда 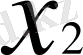нүктесін қабылдасақ,
онда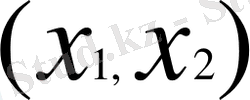кесіндіде сәйкес 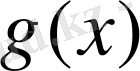интерполяциялық функциясы салынады. Мұндайд
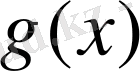салу процессін 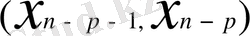интервалына дейін жалғастыруға болатыны айқын.
Салынған 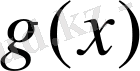интерполяция 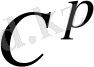тегістеу классының құрама-полиномиалдық
функциясында бар; тор интервалында полиномның дәрежесі 2p+1-ге тең.
Егер p=1 деп қойсақ (кубтық сплайн тегістеуіне сәйкес келеді), онда
бес дәрежелі көпмүшелігімен жұмыс жасаймыз. Көпмүшелік дәрежесі 2-ге
жоғары, бірақ 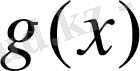тұрғызу үшін сызықтық алгебралық жүйені шешудің қажеті
жоқ.
Тегіс толықтыру жақсы жуықтама қасиеттерін иеленеді. Әсіресе,
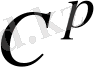классының 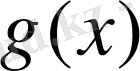толықтырумен көп айнымалылар функциясын
интерполяциялау кезінде, 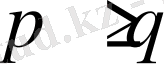болғанда, функцияның өзі үшін және оның
туындылары үшін

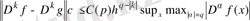(1.3.3)

теңсіздік болады, мұнда мультииндекс

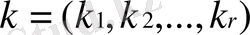
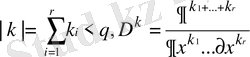
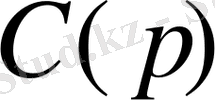
-дан тәуелді және h тор қадамы мен f функциясынан тәуелді емес.
Тегіс толықтыру тағы да бір қасиетті иеленеді. Егер бір түйінді бірге
және қалғандарында нольге тең функциясын, яғни базистік функциясын
тұрғызсақ, онда кез-келген p үшін финитті болады, сонымен тасушының
радиусы p-ны асырмайды. Егер де базистік құрама-кубтық сплайн-функциясын
салатын болсақ, онда ол мүлдем финитті емес. Бұл жағдай ақырғы элемент
әдісімен шешілетін вариациялық есептерде тегіс толықтыруды өте ыңғайлы
етеді.

1.4 Екі немесе бірнеше айнымалылар функциясын интерполяциялау

Құрама-бикубтық функция көмегімен екі өлшемді интерполяциялау
проблемасы көптеген автордық зерттеу пәніне айналды. Біз келесі модельді
есебін қысқаша қарастырамыз.
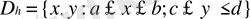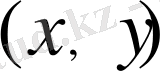-жазықтығының кейбір тікбұрышы. ға тор құрайық.

нүктесінде берілген, осындай құрама-бикубтық функциясының
интерполяциялау есебінің болжамы келесі шарттарды қанағаттандыратын
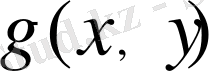функциясын тұрғызумен аяқталады:
1)
(1.4.1)
2) 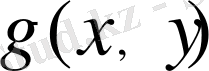торының әрбір ұяшығында бикубтық көпмүшелік түрі болып

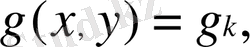(1.4.2)
3) 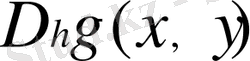торында берілген мәнді қабылдайды.

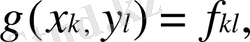
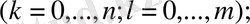(1.4.3)
4) 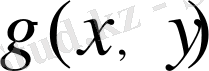функциясы
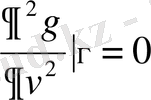(1.4.4) шартын қанағаттандырады (мұнда v-D
облыстың Г шекараға ішкі нормаль).
Мұндай функцияны қалай құруға болады? Былайда, құру бір өлшемдіден еш
айырмашылығы жоқ. 1.1.6 қарапайым формула бойынша кез келген нүктеде
бірөлшемді сплайн–функцияны есептеу үшін функцияның мәнін және оның түйінді
нүктесінде екінші ретті туындысын білу керек екендігін еске түсірейік.
Екінші ретті туындыны табу үшін бір рет үшөлшемді матрицамен сызықтық
алгебралық жүйені шешу керек.
Нақты формула бойынша екіөлшемді жағдайда кез келген нүктеде
функцияны есептеуге болатындай қандай алғашқы есептеулер жасауға болады?
Алдымен тор сызығындағы 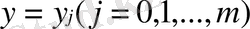кубтық сплайн интерполяциямен бірөлшемді
есептерді қарастырайық. Ол үшін 1.1.9 типінің m+1 сызықтық алгебралық
жүйесін шешеміз. Нәтижесінде тор түйіндегі 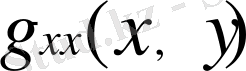функция мәнін табамыз.
Одан кейін сәйкес 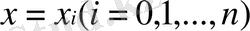сызығындағы бірөлшемді сплайн–интерполяция есебін
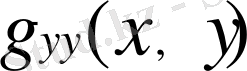шешеміз және торындафункция мәнін табамыз. Енді 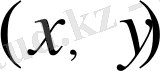- ң кейбір
нүктелерде 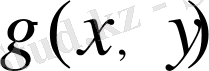мәнін есептеу керек деп болжайық. 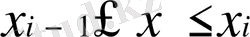, болсын.
(1.1.6) сәйкес 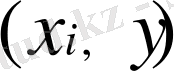, 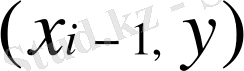нүктелерінде 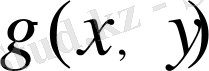мәнін мына формула
бойынша:
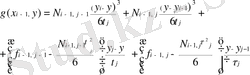, (1.4.5 )

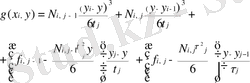(1.4.6)
табуға болады. Мұнда ары қарай , , ,
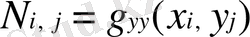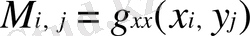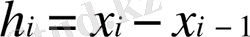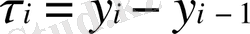
Егер 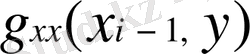және мәндері белгілі болса, онда 1.1.6 типінің формуласы
бойынша 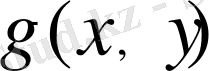мәнін табуға болады.бойынша 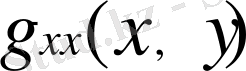функциясы құрама-
кубтық болып табылатынын белгілейміз. Тор мәндері белгілі, 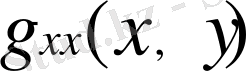функциясы
үшін сызықта m+1 бірөлшемді есебін шешеміз. Нәтижесіндеторында
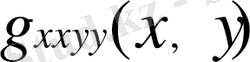функциясын табамыз.
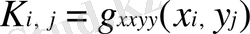белгілесек, онда

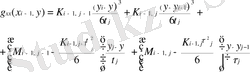(1.4.7)

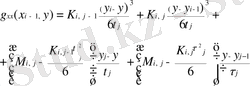
(1.4.8)

Тағы да 1.6 формуласын пайдаланып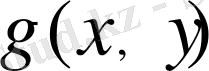мәндерін табамыз:

(1.4.9)

Жоғарыда айтылғандардың бәрін қорытындылай келе, 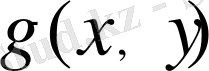бикубтық сплайнды
есептеу үшін қажетті есептеулердің көлемін бағалауға болады. 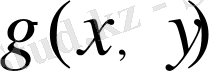керекті
нүктеде есептемес бұрын бір рет (1.1.9) типінің сызықтық алгебралық жүйесін
(n+1)+(m+1)+(m+1)=2m+n+3 шешу керек. Ары қарай облысты бір нүктесінде
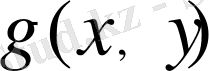функциясын есептеуі үшін (1.1.6) типінің, әсіресе: (1.4.5), (1.4.6),
(1.4.7), (1.4.8), (1.4.9) формулалары бойынша 5 рет есептеулерді орындау
керек. Осы формулалардың тізбегін тордың әрбір ұяшығында 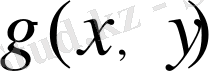полиномиальді
айқын өрнегін алу үшін қолдануға болады. Бірақ та ЭЕМ оперативті жадта
көпмүшеліктің массивтердің коэффициенттерін сақтау үшін 16пт жуық ұяшықты
талап етеді. Бұл алгоритмде айнымалыларды орындарымен ауыстыруға болады
және сонда 2m+n+3 бірөлшемді есептерді шешу керек болады, бірақ соңғы
нәтиже өзгермейді. Сипатталған алгоритм параллелипед типінің көпөлшемді
облыстарында оңай жалпыланған болуы да мүмкін.

1.5 Көп айнымалылар функциясының r – тегіс жуықтауы

Негізгі бөлімде ретсіз торда қатемен берілген көп айнымалылар
функциясын толықтырудың есебіне мүмкін жолдардың ішінен біреуі
қарастырылады. Ұсынылып отырған әдіс негізінде талдауда белгілі бірлікті
бөліктеу түсінігі жатыр. 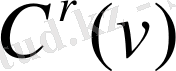классының (- ашық көпмүшелік)
функциясының тізбегі көпмүшелігінде бірлік бөліктеуді жасайды деп
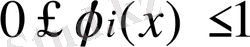айтады, егер және 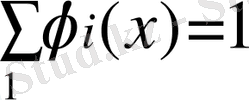барлық үшін.
Әдетте берілген 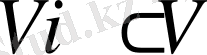ашық көпмүшеден тыс функциясы нольге
бағытталуын талап етеді. (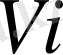)жиынтығы көпмүшелігін бүркейтін
болар. () бірлік бөліктеуді осы бүркеуге бағынышты деп атайды.
Қолданбалы мақсаттар үшін стандартты көпмүшелікпен: m-өлшемді интервалмен
немесе шармен төңіректе ақырғы бүркеу сай. Осы көпмүшеліктің ортасы мен
диаметрі 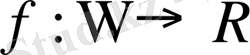функциясының жуықтау қасиеттерімен сәйкес таңдалыну керек.
Алдағы уақытта m-өлшемді кубымен бүркеуді қарастырамыз, ал оларға тәуелді
бірлік бөліктеуді келесі түрде құрамыз.
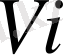кубын 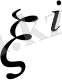ортасы арқылы белгілейміз, ал 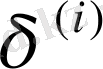арқылы – оның
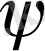
қабырғасының ұзындығын белгілейміз. 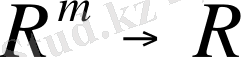классының 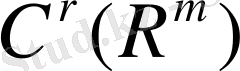егер ,
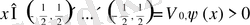егер 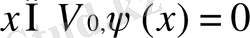болатын стандартты функциямен берілеміз. Мысалы
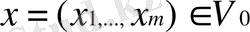(болғанда)
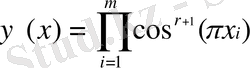немесе
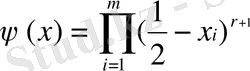
қоюға болады. Енді әрбір i индекс мәні үшін

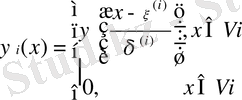
қоямыз. 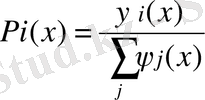функциясы 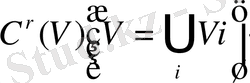класының функциялары болып табылады және
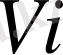бүркеуге тәуелді -да бірлікті бөліктеуді жасайды. Енді әрбір
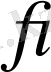функциясынан -ке 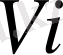- да жақын 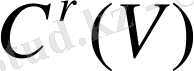класының
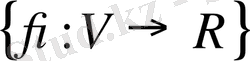функциясының тізбегі 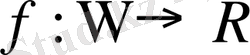функциясы үшін белгілі деп болжаймыз. Әрбір
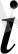үшін бірқалыпты нормада 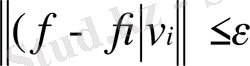болсын. Онда теңдікпен

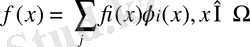(1.5.1)
анықталатын функция - да жақын болады. Шынымен тепе-теңдікке
байланысты 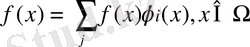әрбір үшін

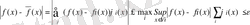
аламыз, яғни .
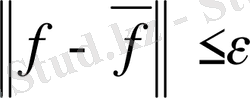Енді функциясын толықтыру үшін бірлікті бөліктеуді қолданамыз;
егер кейбір тор торабында берілген болса, онда 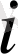үшін
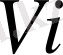кубының, оның 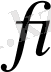төңіректік жуықтауы 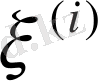ортасына жақын болатын
кейбір жиынтық бойынша 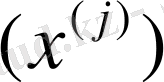торабын құру керек, содан кейін осы жуықтауды
(1.5.1) формуласы бойынша жалғау. Алдағы уақытта біз 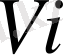кубының
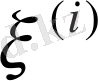орташасымен 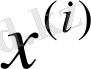түйіні сәйкес келеді деп есептейміз, ал төңіректік
жуықтауы 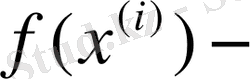ге тең тұрақты функция болып табылады.
Жалғыз жеке жағдайда жуықтау қателігіне баға береміз: 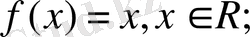тор-
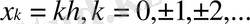нүктесіндегі түйінімен бірқалыпты және шексіз;
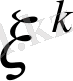интервалдардыңорташалары тор түйінімен сәйкес келеді, ал ,
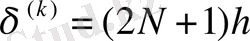мұнда - кейбір натурал сан. бірлікті бөліктеу 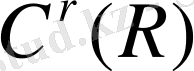класына
тиесілі болсын, 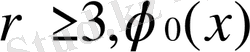функциясы жұп. Мұндай жағдайда қалдық 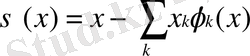өзін тақ,
h периодымен периодты функция түрінде береді. Сондықтан да
1)
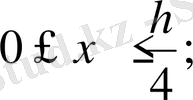
2) 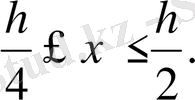жағдайын қарастыру жеткілікті.
1-ші жағдайды қарастырайық. 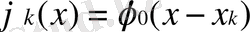және 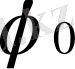функциясы жұп болғандықтан

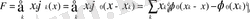
Осыдан Тейлор формуласы бойынша

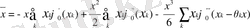
аламыз. Осы теңдіктің оң жақ бөліктегі екінші қосынды нольге тең екені
айқын, сондықтан
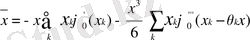(1.5.2)
Ары қарай қосындыға
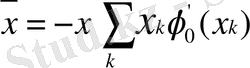
Абельдің түрлендіруін қолданып

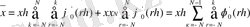
аламыз.
Сондықтан
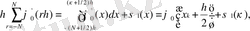
Мұнда
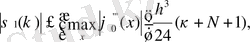(1.5.3)
онда 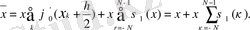(1.5.4)
(1.5.2) (1.5.3) формуласынан бағалауын

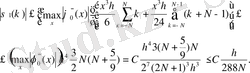(1.5.5)

аламыз. Мұнда С - 3 ретті 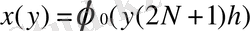функциясының модулінің максималды мәні.
Тұрақты C N-нан тәуелді және N бойымен кемиді.
2 жағдайда да осындай нәтижеге келеміз. Сәйкес бағалауларды сызықтық
функция үшін және бірнеше айнымалылар жағдайында алуға болады [10].

2 Есептік торлар құрудың әдістері

Дифференциалды теңдеу жүйелерін дербес туындымен шешуде жақсы құрылған
есептік торларды қолданып біршама жеңілдетуге болады.Бірақ та
қанағаттандыратындай нәтиже бермеуі мүмкін. Кейбір қосымшаларда есептіқ
торлардың түйіндерінің орналасуының бірдей емес таңдауы тұрақсыздыққа
немесе жинақтылыққа әкелуі мүмкін. Теңдеулерді дербес туындымен сандық шешу
кезінде есептік торларды тұрғызу мәселесі туындайды.
Қарапайым теңдеуді шешіп көрейік,

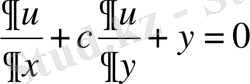
кейбір аймақтарында бастапқы және ақырғы шарттарымен сәйкес. Есептеу әдетте
есептеу кеңістікте жүргізіледі. Бастапқы дифференциалдық теңдеуінің дербес
туындысы x, y физикалық координатасынан есептік кеңістік
координатасына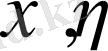өтуі күрделі дифференциалдық функциялардың ережелерінің
көмегімен түрленеді:

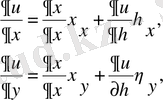(2.1)
Онда ол мынандай түрде болады:

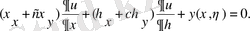
(2.2)
Осы теңдеу есептеу кеңістігінде бірқалыпты торда шешіледі. Міндетті түрде
физикалық кеңістік пен есептеу кеңістіктегі координаталарының арасына
байланыс орнату керек. Бұл байланысты түрленудің метрикалық коэффициенттері
береді ( 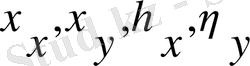мүшелері қарастырылған теңдеуде дербес туындысымен).

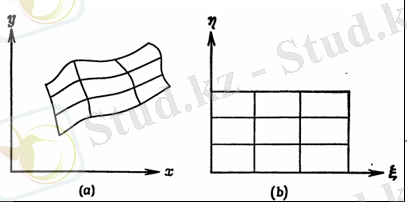
Сурет 1. Физикалық кеңістіктің есептеуіш кеңістігіндегі кескіні: а)
физикалық кеңістік ; b) есептеуіш кеңістік

Есептік торларды құру есебі тор түйіндісін физикалық кеңістіктен (D)
есептеуіш кеңістікке (CD) ауыстыратын кескінді табудан тұрады. Бұл кескін
кейбір талаптарды қанағаттандыру керек. Солардың ішінен кейбіреуін атап
кетуге болады:
1. Кескін бірмәнді болу керек.
2. Тор сызығы тегіс болу керек, ол туындынының үзіліссіздігін қамтамасыз
етеді.
3. Тор (D) аймағының үлкен сандық қателіктер туындайтын бөлігіне қалың болу
керек.
Бірөлшемді есептеуіш тор құру оңайлау. Бұл торларды тұрғызуда көптеген
функциялар немесе әдістер бар. Сондықтан көбінесе екі өлшемді тор тұрғызуда
сұрақтар туындайды. Ал үшөлшемді тор тұрғызу өте күрделі есеп болып
табылады және қанағаттандыратындай нәтиже беретін әдістер сондай көп емес.

Есептеуіш тор құру әдістерін дөрекі түрде 3 классқа бөлуге болады:
1. Комплекстік айнымалы функциялар теориясының әдістері.
2. Алгебралық әдістер.
3. Дифференциалдық теңдеулерді шешуге негізделген әдістер.
Біз алгебралық әдістер мен дифференциалдық теңдеулерді шешуге негізделген
әдістерін қарастырамыз. Жалпы алгебралық әдістер мен дифференциалдық
теңдеулерді шешуге негізделген әдістерді күрделі үшөлшемді есептерге
қолданылады. Бұл екі әдіс есептеуіш торларды құру әдістерінің ішіндегі
тиімді және кең таралған болып табылады.

2.1 Алгебралық әдістер. Дифференциалдық теңдеулерді

шешуге негізделген әдістер

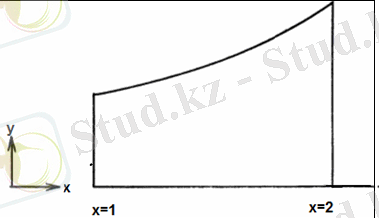
Сурет 2.

Тор тұрғызу кезінде есептеуіш кеңістік тік бұрышты болу міндетті емес.
2-суретте көрсетілген кескінде тор тұрғызу керек болсын. Оның қабырғасы
функциямен беріледі:

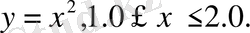(2.1.1)

Бұл мысалда x координатасы бойынша тұрақты қадамды таңдай отырып және
соплоның осьі мен қабырғасы арасындағы әрбір кесіндіні бірдей бөлікке бөле
отырып тор тұрғызу оңай. Бұл процедура келесі тәуелдімен сипатталады:

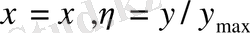(2.1.2)
мұнда 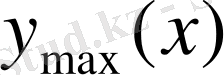- сопло қабырғасының теңдеуі. Осыдан берілг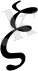ен мен
мәндері бойынша x пен y мәндерін табу оңай. Физикалық кеңістікте
тұрғызылған тор 2.3- ші суретте кескінделген.
Түрлендірудің метрикалық коэффициенттерін есептеуде мұқият болу
керек. (2.1.2) теңдеуі бойынша есептелетін, дербес, 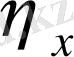пен
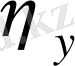туындылар келесі түрде болады:

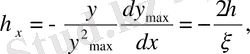(2.1.3)

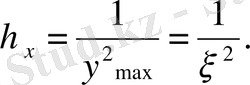(2.1.4)
Осы қарастырылған мысалда түрлену аналитикалық түрде болды және соның
көмегімен бірден тор түйіндерінің таралуын алдық.

Сурет 3. Физикалық кеңістіктегі есептік тор

Мынандай түрлендіруді нүктелерді физикалық кеңістікте бере отырып және
орталық айырымды қолданылуымен метрикалық коэффициенттерді сандық түрде
есептей отырып құруға болады. Бірақ бұл жағдайда түрлену алгебралық емес,
сандық болып саналады.
Дифференциалдық теңдеулерді шешуге негізделген әдістерге тоқталсақ.
Жоғарыда есептік тор құруда алгебралық әдісті қарастырдық.
Дифференциалдық теңдеулерді шешуге негізделген әдістерді тор құруда
қолданған кезде осы теңдеулердің шешу қасиеттерін ескеруге болады. Бұл
мақсатта әдетте Лаплас пен Пуассонның теңдеулері қолданылады. Лаплас
теңдеуін таңдау себебін Дирихленің шекаралық шартымен екі өлшемде стационар
жылуөткізгіштік есебін қарастырған кезде түсінікті болады. Бұл есептің
шешімі тегіс (екінші ретті туындысы бар және үздіксіз) және қиюшы емес
изотермаларды береді. Берілген облыста изотерма саны көз мүшесін қосылуымен
көбеюі мүмкін. Егер тор сызығынан изотерманы алатын болсақ, онда соңғылары
тегіс және үзіліссіз болады. Көз мүшесінің мөлшерін кез келген аймақта
олардың қоюлануынмен басқаруға болады.
Томпсон және т.б. тор тұрғызуда эллипстік теңдеуінің дербес туындысын
қолдануда көп еңбек етті. Бұл процедура Уинслоу қолдануында үйлесімді; ол
физикалық кеңістіктен есептеуіш кеңістікке түрлендіреді, сонымен қатар
кескін Пуассон теңдеуімен сәйкес жүзеге асады. Бұл кескін физикалық
облыстың шекарасында тор нүктелердің берілуімен салынады. Ондай болса
ішкі түйіндерінің таралуы келесі теңдеудің шешімімен анықталады:

(2.1.5)

мұнда - есептеуіш аймағындағы координаталары, ал мен
мүшелері арқылы D – ның ішіне түйіндердің орналасуын басқару жүзеге асады.
Ары қарай (2.1.5) теңдеуінде тәуелсіз айнымалалар үшін координаталары
есептеуіш кеңістікте қолданылады, одан барып біз екі эллипстік теңдеулер
жүйесін аламыз:

(2.1.6)
Мұнда

Бұл теңдеуді есептеуіш кеңістікте () бірқалыпты торда шешеді, ол
физикалық кеңістікте әрбір түйінінде координатасын береді. Қарапайым
байланысқан аймақ үшін Дирихленің шекаралық шарты барлық нүктесінде
қолданылуы мүмкін. Мұндай әдіс тор тұрғызуда көп құндылыққа ие. Тор тегіс,
түрлендіру бірмәнді болып шығады, ал күрделі формадағы шекаралар оңай
өңделеді. Әрине, әдістің кемшіліктері де болады. мен - беру
қарапайым есеп болып табылмайды, ішкі бөліктерде тор түйіндерінің
орналасуын басқару қиын, және де аймақтың шекарасы уақытқа байланысты
өзгеріп отыруы да мүмкін. Соңғы жағдайда тор уақыт бойынша әрбір қадамнан
кейін құрылып отыру керек, ол машиналы уақыттың көп жұмсалуына әкеп
соқтырады.
Томпсон әдісіне қарапайым мысал 4 суретте көрсетілген. Екі
шоғырланған шеңбердің арасындағы аймақ есептеуіш кеңістікте тікбұрышта
кескінделген. Суретте физикалық кеңістікте тұрақтылық мен
сызығын есептеуде алынған нәтиже көрсетілген. Ішкі шеңбер радиусына
ие, сыртқы - радиусына ие. Бұл есепте шеңберді радиусы бойынша
кеседі және олардың арасындағы іші тікбұрышта координаталардың 1-ден -
ке дейін және 1-ден - ке дейін есептеуіш кеңістікте өзгеруі
кескінделген. Бұл жерде кескін Лаплас теңдеуінен шекаралық шартымен
анықталады:

Шешім келесі түрге ие:

(2.1.7)
мұнда

Бірақ осы жағдайда шешім физикалық аймақта бірқалыпты торды бермейтіні
қызық. Тор шоғырланған шеңберлердің жиынтығы болып табылады.

Сурет 4. Томпсон әдісін қолдану: а) физикалық кеңістік ; b) есептеуіш
кеңістік

Бұл шеңберлерді бір бірінен тең тұрғызу үшін және деп беру
керек. Қажетті түйіндерінің орналасуын алу үшін мен
дістемесімен орналастыру керек. Миддлкофф пен Томас бұл әдістемесіні
зерттеген.
Бұл ойды түсіндіру үшін (2.1.5) теңдеуін Дирихле шекарасымен шешу қажет
болсын делік. Келесі мен -дің келесі жазба формасын таңдаймыз:

( 2.1.8)
мұнда мен төменгі шекаралық шекарадан анықталады. Осы бастапқы
(2.1.5) теңдеу жүйесін келесі түрде жазуға болады:

(2.1.9)
Жақша ішіндегі тұрған өрнекті шекарада нөлге теңестіріп, пен
функцияларын анықтаймыз. Миддлкофф пен Томас шекара шеті болғанда
келесі шарттың орындалуын талап етті:

(2.1.10)
Шекараның барлық нүктелерінде x пен y белгілі болғандықтан, мен
функциясын (2.1.9), (2.1.10) теңдеулеріне кіретін барлық туындылар үшін
орталық айырымдық жуықтаманы қолдану арқылы анықталуы мүмкін. мен
әрбір (2.1.9), (2.1.10) жұп теңдеуінен біреуі бойынша анықталады.
(2.1.10) теңдеуінен, (2.1.9) теңдеуінен анықтаймыз. Осы ыңғайды
қолданып мен шекарада табылады, ал ішкі аймақта бұл
функциялардың мәндері қарапайым экстраполяциямен алынады.Осы әдістеме
шекарада тор түйіндердің таралуын басқару тәсілін береді. Тор түйіндердің
таралуына бақылауда басқа да әдістемелер ұсынылған. Томсон жұмысын ұсынуға
болады.
Есептік тор құру үшін теңдеулер дербес туындысымен қолданылуы мүмкін.
Кейбір дене айналасына тор құру үшін Стегер мен Соренсон гиперболалық
теңдеулер жүйесін қолданатын әдісті сипаттады. Бұл кезде ішкі шекара алдын
ала көрсетілмейді. Дененің беті ішкі шекараны жасайды және гиперболалық
теңдеулер жүйесі ішкі шекараны беруді қажет етпейтін марштау әдісімен
шешіледі. Стегер мен Соренсон ортогональ тор құруға әкеп соқтыратын доға
әдісі мен көлем әдісін ұсынады. Кейінірек тоқталамыз.
Екі өлшемді якобиан жағдайда түрлену физикалық пен есептік кеңістіктегі
тор ұяшықтар ауданына арақатынасты береді. Егер есептік жазықтықта тор
ұяшықтардың өлшемін бірге тең деп алсақ , яғни оның ауданы да бірге
тең болады. Онда шама

(2.1.11)
есептік кеңістіктегі тор ұяшығының ауданында бар.Егер функцияның
координаты деп санайтын болсақ, онда (2.1.11) теңдеуін есептік кеңістіктегі
торды бақылау үшін қолдануға болады. Екінші теңдеуді физикалық
кеңістіктегі шекарада тор сызығының ортогональ шартынан аламыз. Сондықтан
да шекара шетін

(2.1.12)
осылай жазуға болады немесе

(2.1.13)
Сызық шеті

(2.1.14)
Егер мен тұрақтылық сызығы перпендикуляр болса, онда
жазықтығында осы сызықтың көлбеулік бұрыш тангенстердің арасында қатынас
орнатылуы керек

немесе есеппен (2.1.13), (2.1.14)

(2.1.15)
(2.1.11), (2.1.12), (2.1.13), (2.1.14) теңдеулер жүйесі кейбір белгілі
айналасына қатарға жіктелгендерді сызықтандырады. (2.1.11) теңдеу
мүшелерінің біреуі былай жазылады:

(2.1.16)
Егер қалған мүшелерін аналогиялық түрде сызықтандыратын болсақ, онда

(2.1.17)
мұнда

( 2.1.18)
матрицаларының өзіндік мәндері нақты болу керек, егер
бағытталған жүйе гиперболалық болса. Олар

(2.1.19)
тең. Соңғы теңдік (2.1.17) гиперболалық теңдеуі координатасы бойынша
және оны бағыты бойынша болғанша марштау әдісімен шешуге болады.

Сипатталған процедурада тор салуда беті дененің бетімен сәйкес
келеді және оның шетінде тор түйіндері берілген деп есептеледі.

а) b)

Сурет 5. Бетіне жақын элементар ұяшық ауданын есептеу: а) физикалық
аймақтағы тор; b) ұяшық ауданымен берілген есептік кеңістіктегі тор

Ары қарай (2.1.12) теңдеуінен анықтау керек. Бұны Стегер мен Соренсон
беттің шетіне ұзындығы денесінің ұзындығына тең түзу сызықты сала
отырып және осы сызыққа дененің бетінде берілген түйіндердің таралуын
нұсқай отырып жасауға болатынын ұсынады. Содан соң келесі сызықты
параллель жүргізеді. Осыдан барып шаманы тор ұяшықтарының
ауданының мәні бойынша оңай анықтайды. Сурет 5 осы процедураны суреттейді.
Енді 2.1.13 теңдеу жүйесін әдеттегідей гиперболалық теңдеулер сияқты
шешеді. Біз бұл әдісте шамасын бергендіктен, тегіс торды сала аламыз,
егер сәтті таңдалған болса. Және де керсінше - дің сәтсіз
таңдалынуы сынуға (майысуға) әкеп соқтырады немесе тор бойынша шекаралық
түйіндердің күйі жайлы ақпараттың таралуы бұрмаланған. Сонымен қатар
шекарадағы берілгендердің үзілуі осындай торда жіберіледі. Бір жағынан
осындай әдіспен тез ортогональды тор салынады. Мына сурет 6 айналасы
типтік профильмен салынған тор көрсетілген.

Сурет 6. Айналасы типтік профильмен салынған есептік тор

Мұнда денеге жақын нүктелердің таралуы тұтқыр орналасқан қабатты шешуге
мүмкіндік береді.
Жоғарыда сипатталған әдістер, теңдеулерді дербес туындысымен шешпес
бұрын, тор түйіндердің таралуы белгілі болу керек екендігін талап етеді.

2.2 Бір байланысты аймақ

Бірбайланысты аймақ, ішінде жатқан кез келген тұйық контурдың аймақ
шекарасына жатпайтын нүктесіне жинауға болатындығымен сипатталады.
Қарапайым кескінде төрт қисық сызықпен анықталған аймақты бейнелеуде,
есептік аймақта тікбұрышты түрде түрленеді. Осыған сәйкес кескін мына
суретте бейнеленген.

Сурет 16. Екіөлшемді қисайған канал

Егер физикалық аймақ қандай да бір арнайы пішіннен тұрса, онда
есептік аймақта да осы пішінді кейде сақтап қалуға болады. Мысалы, сурет 17-
те қисықсызықты физикалық аймақтың L-бейнелі пішіні есептік аймақтың
тікбұрышты L-бейнелі пішініне қалай түрленетіні көрсетілген. Суреттен
осындай түрленудін негізгі артықшылықтары көрінеді. Аймақтың пішінін
жуықтап сақтау кезінде тордың қатты өзгерістен, яғни пішіннің бұзылуынан
қашқан жөн.
Дәл сол физикалық аймақтың L-бейнелі пішіні есептік аймақта
тікбұрышты түрге түрленуі мүмкін (сурет 18). Енді, физикалық аймақта
бейнеленген сынықтың және нүктелері есептік аймақта
тұрақты мәнінің (жәненүктелері) сызығында жатыр.

Сурет 17. Пішінді сақтаумен L-бейнелі пішіннің түрленуі

Мына суретте көрсетілген аймақта сандық алгоритмді салу, сурет 17-де
көрсетілген аймақтан қарағанда қарапайымдырақ.

Сурет 18. L-бейнелі аймақтың тікбұрышқа түрленуі

Алайда физикалық аймақтажәне нүктелеріне жақын тордың қатты
бұзылуы немесе өзгеруі дәлдікті жоғалтуға әкеп соқтырады, сурет 17-дегі
тордан қарағанда.
Есептік аймақтың бұрыш нүктелері физикалық аймақтың тегіс шекара
маңайында жатса (сурет 19), онда кері жағдай туындайды. Осындай жағдайда
, және т.б нүктелеріне жақын торлар физикалық аймақта қатты
қисайған болар, және мұнда шешімнің дәлдігін локальді жоғалуын күтуге
болады. Cонымен қатар, есептік аймақтың шекара бойынша нүктесіне өту
кезінде координат сызығынан координат сызығына өту жүреді.

Сурет 19. Физикалық аймақтағы жалған бұрыштар

Физикалық аймақ шекарасының пішіні күрделі болған сайын, ықтимал кескіннің
саны да үлкен болады. Мысалы, сурет 20-21-де бейнеленген бірдей аймақ әр
түрлі тәсілдермен кескінделуі мүмкін.

20 сурет. Жеке дөңестің тегістелуі

Дөңестік үшін (сурет 20-да бейнеленген) аз мәні кезінде қоюландырған
торды енгізудемен нүктелеріне жақын жақсы шешімді алуға мүмкіндік
береді. Сонымен мен нүктелеріне жақын сондай ұсақ торлар алынады.
Алайда егерконтуры тұтқыр тасқында орналасса және шекара кіріс
шекара болып табылатын болса, онда меннүктелері тежегіш нүктелері
болады. Сурет 21-де мен нүктелері есептік аймақта бірдей нүктеге
барып түседі. Мұндай тор Сурет 21-де көрсетілген тормен салыстырғанда, аз
ортақ нүктелерде шекараларына жақын үлкен қоюландыруды алуға мүмкіндік
береді. Алайда Сурет 21-дегі нүктесіне жақын тор қатты өзгертілген
болып шығады.

Сурет 21. Дөңестің жазықтыққа түрленуі

Осындай тор шекарасы арқылы кіретін, ал мен арқылы шығатын
модельдеу ағымында қабылданады.
Егер және нүктелері кедергісіне жетерліктей алыс еркін
ағында орналасса, онда шекараның жақсырақ кескіні сурет 22-де көрсетілген
кескін болып табылады.

Сурет 22. Дөңестің жақсы локальді шешіммен тегістелуі

Бұл кескін қандай да бір дәрежеде сурет 20-да кескінге ұқсас, және
нүктелеріне жақын орналасқан тордың бүлінген бөлігін ескермегенде.
және нүктелеріне жақын ағын біркелкі болғандықтан, тордың
локальді өзгеруімен байланысты қателіктер, сурет 20-да бейнеленген кескін
үшін аз болады.
Есептік аймақта физикалық шекараны кескіндеу кезінде күтілетін шешімде
туындаған тордың өзгеру әсерін ескеру қажет. Егер өзгеру біркелкі ағынның
аймағында жүрсе, локальді тордың өзгеруі жалпы шешімнің дәлдігіне аз әсер
ететіндігін; қызығушылық танытатын аймақтан қашу керек екендігін ескеру
керек.

2.3 Көп байланысты аймақ

Көпбайланысты аймаққа мысал болып бір немесе одан да көп кедергінің
маңайындағы ішкі ағымдар қызмет етеді. Каналдағы кедергінің маңайындағы
ағымдар, мысалы жылу алмасуда, басқа бір мысал болып табылады. Шекараның
жақсырақ кескіні кедергінің пішініне тәуелді.
Бұрышты дене үшін есептік жазықтықта тікбұрышты немесе квадрат
шекараларының кескіні қабылдануы мүмкін; сонымен қатар көпбайланысты аймақ
сақталады. Бұл жағдай сурет 23-те бейнеленген.

Сурет 23. Бұрышты дененің кескіні

Физикалық аймақтағы тор біршама аздап қисайған. Егер дене жіңішке
болса, онда оны сурет 24-те көрсетілгендей, есептік аймақта тілікке
кескіндеуге болады. Физикалық аймақтағы нүктесіне жақын тордың қисаюы
негізгі ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.