Реттік статистикалар үлестірімі

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 40 бет
Таңдаулыға:

Дипломдық жұмыс 3 тарудан жалпы алғанда 52 беттен тұрады. Жұмыста 6
әдебиеттерге сілтеме жасалған. Жұмыстың сипатын білдіретін түйін сөздер:
реттік статисткалар, толерантты параметрсіз интервалдар, Марков тізбесі,
туындатқыш функциялар, рекурренттік қатынастар
Дипломдық жұмыста реттік статистикалардың қолданылымдары,
үлестірімдері және үлестірімдерін табуға арналған есептер қарастырылған.
Дипломдық жұмыстың мақсаты – реттік статистикалардың үлестірімдерімен,
қолданылымдарымен және оларға байланысты есептермен танысу.

Мазмұны

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ... ... ... ... ..4
І Тарау
§1.Реттік
статистика ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... 5
1.1Реттік статистика
ұғымы ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... .5
1.2Материал қамту
кеңдігі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... .7
1.3Белгілеулер ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ... ... ... .9
II Тарау
§2.Реттік статистикалардың үлестірім теориясының
негіздері ... ... ... ... ... ... .1 3
2.1Реттік статистикалар
үлестірімі ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ... 13
2.2Реттік статистикалардың екі немесе одан көп сандардың ортақ
үлестірімі ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ... ... ... ...15
2.3Құлаштың және басқа жүйелі статистикалардың
үлестірімдері ... ... ... ... ... .. ...17
2.4Дискретті үлестірім үшін реттік
статистикалар ... ... ... ... ... .. ... ... ... ... ... ... ... ..20
2.5Квантиль үшін параметрсіз сенімділік
интервалдар ... ... ... ... ... ... ... ... ... ... ... .21
2.6Толерантты параметрсіз
интервалдар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
...25
2.7Тәуелсіздікпен байланысты нәтижелер – Марков тізбесі секілді реттік
статистикалар ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ... ... ...27
ІІІ Тарау
§3Реттік статистикалардың
моменттері ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... .3
2
3.1Негізгі
формулалар ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... .32
3.2Қалыпты
үлестірім ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... 39
3.3Дискретті
жағдай ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... 44
3.4.Рекурренттік
қатынастар ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ..47
Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ... ... 51
Қолданылған әдебиеттер
тізімі ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ... 52
Кіріспе

Дипломдық жұмыстың мақсаты – реттік статистикалардың
үлестірімдерімен, қолданылымдарымен және оларға байланысты есептермен
танысу.
Бұл дипломдық жұмыста реттік статистикалардың қолданылымдары,
үлестірімдері және үлестірімдерін табуға арналған есептер қарастырылады.
Реттік статистикалар ғарыштық кемелерде бөлшектер санын есептеуде,
параметрлерді бағалауда, үлестірім түрін тексеруде және т.б қолданылатыны
мойындалған жайт.
Бұл жұмыста біз реттік статистикаларға байланысты есептерді көптеген
әдістермен және түрлендірулер енгізу арқылы зерттейміз. Біз әрбір
параграфтың соңында қарастырылған тақырыптарға байланысты, оларды
негіздейтін мысалдар қарастырып, жекелеген есептер шығардық, олардан
қорытындылар алдық.
Алғашқы параграфта реттік статистика пәні ұғымы енгізіліп, оның
статистикадағы ролі, қолданылымдары қарастырылған. Бұру және масштаб
параметрлерін бағалауда Гаусс-Марков теоремасының көмегімен жүйелі түрде
реттік статистиканың сызықты функцияларын пайдалануға болатынына және де
өмір ұзақтығына жүргізілетін тәжірибелерде реттік статистикалардың маңызы
зор екендігіне көз жеткіздік.
Екінші тарауда реттік статистикалардың үлестірімдері, дискретті
жағдай үшін үлестірімдер, квантиль үшін параметрсіз сенімділік
интервалдары, тәуелсіздікпен байланысты нәтижелерді қарастырамыз. Бұл
нәтижелерден маңызды қорытынды шығарамыз және олар өмір сүру ұзақтығына
жүргізілген сынақтар есебінде маңызды қолданылымдарға ие болатындығын
көреміз.
Үшінші тарауда біз реттік статистикалардың әр түрлі моменттерін
(математикалық күтімін, дисперсия және ковариация) қарастырамыз. Ары қарай
біз реттік статистикалардың сызықты функциялары параметрлерді бағалауда өте
пайдалы екеніне көз жеткіземіз. Моменттерді анықтауда қалыпты, дискретті
жағдайларды, моменттер арасындағы рекурренттік қатынастарды қарастырамыз.

І Тарау
§1.Реттік статистика
1.1 Реттік статистика ұғымы
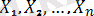
Егер 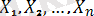, кездейсоқ шамалары мағыналары бойынша

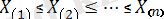
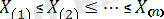
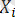
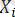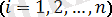
өсу ретімен орналасса, онда – ді і – ші 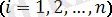реттік статистика деп
атаймыз. Әдетте, әрқашан болмаса да, ( ретсіз статистикалар )
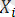
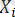статистикалық тұрғыдан тәуелсіз және бірдей орналасқан; бір-бірінің
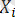
арасындағы теңсіздіктен 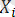шамалары тәуелді.
Реттік статистика пәні осы реттелген кездейсоқ шамалардың қасиеттері
мен қолданылымдарымен және олардың функцияларымен байланысты. Мысал ретінде
X(n) және X(1) экстремальды мағыналар, Wn = X(n) - X(1) құлаш, максимальды
ауытқу (орташа таңдаудан) X(n) - X және кездейсоқ таңдама үшін N(µ,δ2)
қалыпты үлестірімнен алынған стьюденттелген құлаш WS, мұндағы Sv - δ2
үшін ν еркіндік дәрежесі бар ортаквадраттық бағаны алуға болады. Бұл
статистикалардың барлығы маңызды қолданылымдарға ие. Су басу мен
құрғақшылықты статистикалық зерттеу кезінде экстремальды жағдайлар
туындайды, сонымен қатар материалдардың күйреуімен байланысты беріктілікті
жарылуға және басқа проблемаларды зерттейтін есептер де туындайды.
Бәрімізге белгілі δ үшін құлаш жылдам есептелетін баға болып табылады және
сапаны бақылау есептерінде ерекше кең қолданылымдарды табады. Экстремальды
ауытқулар қалдықтарды табудың негізгі құралы болып табылады, үлкен шамалар
Xn бір немесе бірнеше аномальды бақылаулардың қатысуын көрсетеді.
Стьюдентелген құлаш қалдықтар тек бір бағытта пайда болған жағдайда ғана
пайдалы емес. Сонымен қатар , ол дисперсиялық талдаудың аздаған
ранжирленген орташа есептері үшін көптеген жылдам критерийлердің негізін
құрастырады. Жылжу параметрлерін және масштабты бағалау үшін аз квадраттар
туралы Гаусс - Марков теоремасының көмегімен реттік статистикалардың
сызықтық функцияларын системалық түрде пайдалануға болады. Мұндай
қолданулар әсіресе сұрыптаудағы бақылаулар цензураланған жағдайда пайдалы,
дәл бұл жағдайда стандартты бағалау әдістері еңбекті немесе
қанағаттанарлықсыз болады. Өмір ұзақтығына жүргізілетін сынақтар
цензураланған мәліметтер үшін реттік статистикалардың нағыз артықшылықтарын
береді. Дәл осылай мұндай тәжірибелер толық аяқталуына дейін өте ұзақ
жалғаса алатындықтан, онда сынаққа ұшыраған n біртекті заттардың ішінен
бірінші r заттардың істен шығуынан кейін тәжірибені жиі тоқтатқан жөн.
Бақылаулар болып табылатын істен шыққан r моменттер басқа жағдайларға
қарағанда өзіміз үшін тәжірибе әдісімен реттелген, олар арқылы орташа өмір
ұзақтығы сияқты қажет параметрлерді бағалай аламыз. Соңғы жылдары реттік
статистикаларды зерттеу қатар бағытында жаңа түрткі пайда болуына себеп
болды. Есептеуіш машиналар бірдей мәліметтерге көптеген әр түрлі
көзқараспен қарауға, сондай-ақ көп жақты, "мәліметтерді талдау" деген
жалпы атауға ие болған жиі ресми емес қабылдаулар қолдануға мүмкіндік
береді. Мәліметтер болжанған (а) үлестіру және болжанған (б) үлгімен
сәйкестікте бола ма? Ықтималдықты қағазда болжанған үлестірімге сай кейбір
қарапайым функциялардың рангілерінің реттелген бақылауларын салыстыра
отырып, (а) есебінің шешіміне жол табуға болады. Ықтималдықты сызбаға
лайық түзу барлығы дұрыс екенін көрсетеді, бұл уақытта күрделі ауытқулар
түзуден аномальды бақылаулардың және басқа да болжанған үлестірімдердің
қателіктерінің қатысуын табуға көмектеседі. Осындай ретпен, (б) сұрағына
жауап бере отырып , сызбада болжанған үлгідегі реттелген қалдықтарды
келтіруге болады. Осылай сияқты статистикалар мен критерийлерге іздеу
жүргізіледі, олар саналы шарттарда (мысалы, нормальды теорияда ) үйлесімді
болмаса да тәжірибеде кездесетін әр түрлі жағдайларда жақсы жұмыс істейді.
Қалыпты жағдайда лайықты k таңдауында нәтижелілік жоғалтуы лақтыруларға
сезімталдықтың жоқ болуымен немесе болжанған үлестірімнің басқа ауытқуымен
компенсацияланады. Әйтеуір, біз арнайы тақырыпқа, бірақ ғарыштық ғасырға
лайық қосымшаларға көңіл аудара аламыз. Үлкен таңдамаларда (мысалы,
ғарыштық кемеде кішкентай бөлшектердің санын есептеуде) мәліметтерді
қысқартуға қызықты мүмкіншіліктер бар ( Эйзенберг және Познер (1965)),
жерде қанағаттанарлықтай параметрлерге бағалау жасау үшін және болжанған
үлестірім түрін тексеру үшін таңдаманы реттік статистикалардың жеткілікті
санымен ауыстыруға болады (ғарыштық кеме компьютерінде).

§1.2 Материал қамту кеңдігі

Жоғарыда айтылған барлық сұрақтарға көңіл бөлсек те, реттік
статистикалар статистиканың әр түрлі ауқымында кездесетіндіктен,
материалмен шектелуімізге тура келеді. Уилксқа(1948) қарағанда, біз "реттік
статистика" терминін қазір жаппай қабылданған тар мағынада көбірек
қолданамыз, бақылаулардың реттілігін талап ететін, Вилкоксонның екітаңдаулы
статистикасына мысал болып келетін "рангтік реттік статистикаларды"
пайдаланбаймыз. Рангтік реттелген статистикалардың ерекшелігі, олар нақты
мағыналарынан емес, тек реттелген бақылаулардың рангілерінен ғана тәуелді
болады, демек, олар ең болмағанда үзіліссіз кездейсоқ шамаларды параметрсіз
немесе толассыз үлестіру әдісіне әкеліп соғады. Реттік статистикалардан
негізі алынған процедуралардың көпшілігі басқа жағынан қарастырылған
үлестірімнің түрінен тәуелді болады. Бірақ реттік статистикалардың теориясы
көптеген параметрсіз есептерде(мақсаттарда) пайдалы, сонымен қатар рангтік
критерийлердің қасиеттерін зерттеуде, мысалы функция қуаттылығының
көмегінде.
Қалған шектеулер кітапта көбінесе жеке мінезде болады. Реттік
статистикалар көптеген салыстырулар мен орташалардың ранжирленген сияқты
күрделі процедураларда шешім қабылдауда маңызды көмекші роль ойнайды.
Біздің пікірімізше, бұл жерде қарастырып отырған пән үшін статистикалық
шешім теориясының элементтерін дамыту қажет емес екенін Миллердің(1966)
пайдалы кітабынан және аз дәрежеде Бекхофердің(1968) монографиясынан
көреміз(дегенмен осы үшін реттік статистикалар теориясы осы жерде
келтірілгені анық, немесе қарапайым ой- түйіндеулер арқылы шығарылуы
мүмкін). Бірақ аномальды бақылауларды өңдеуге арналған кейбір күрделі
процедуралар 8 тарауда қарастырылған.
9 тарауға қарағанда көбірек жасалған асимптоталық әдістер туралы
айтуға болар еді. Бірақ бұл сұрақтың практикалық жағы маңызды дәрежеде
Гумбельдің (1965) кітабында көрсетілген. Басқа жағынан , соңғы жылдары
маңызды дәрежеде ілгері жылжытылған теория математикаға көбірек жақындады,
оны осы теория бойынша құралған күрделі монографиядан көреміз. Кейбір
маңызды нәтижелерді қараумен және басқа зерттеулерге түйін келтірумен
шектелген дұрыс деп есептейміз.
Реттік статистикалардың техникасын нәтижелі пайдалану көп таблицаларды
талап етеді. Тіпті ішіндегі тек пайдалыларды қосу кітаптың көлемін едәуір
үлкейтер еді. Сондықтан біз көркемдеуге арналған бірнеше кестелермен
шектелдік, ал қалғандарына келетін болсақ, оқырмандарды Пирсон, Хартли
(1966) кестелері сияқты және әсіресе Сархан мен Гринберг (1970)
кітабындағы кең кестелер терімінежібереміз. Мақалаларда орналасқан
кестелерге кітаптың ішінде сілтемелер көп, ал түсініктер Қосымшада
келтіріледі.

§1.3Белгілеулер

Бұл параграф сілтемелер үшін қызмет етсе де, оқырман ары қарай өтпес
бұрын оны дұрыс қарап шығуы керек. Мүмкіндігінше, кездейсоқ шамалар (немесе
жай шамалар) бас әріптермен белгіленеді , ал олардың орындалуы (бақылау )
лайықты жол әріптермен белгіленеді. Реттік статистикаларды не реттелген
шамалар деп, не реттелген бақылаулар деп түсінеміз. Олай болса,
Х1, Х2,..., Хn – ретсіз шамалар;
х1, х2,..., хn – ретсіз бақылаулар;
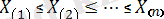
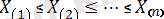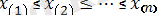
{ – реттелген шамалар; 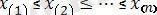– реттелген бақылаулар;} – реттік
статистикалар;
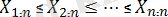
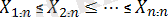– реттелген шамалар- жазудың толық түрі.
Таңдама көлемін көрсету үшін, нақты қысқа үлгіден жеткілікті кең
түріне көшу арқылы біз нақты белгілеу үлгісін пайдалана аламыз.
Р(х) = Р(Х ≤ х) – Х кездейсоқ шамасының үлестірім функциясы;
Р(х):
1) үзіліссіз кездейсоқ шама үшін үлестірім тығыздығы;
2) дискретті кездейсоқ шама үшін ықтималдық функциясы;
Fr(x), Fr:n(x) – Xr, Xr:n, r = 1,2,...,n кездейсоқ шамасының үлестірім
функциясы;
fr(x), fr:n(x) – xr, xr:n кездейсоқ шамасының ықтималдық функциясы немесе
үлестірім тығыздығы;
Frs(x,y) = P( X(r)≤x, X(s)≤y ) – және X(s) кездейсоқ шамаларының ортақ
үлестірім функциясы;
f rs(x,y) - X(r) және X(s) кездейсоқ шамаларының ықтималдық функциясы
немесе ортақ үлестірім тығыздығы;
ξp – үлестірім үшін p ретінің квантилі, яғни P(ξp) = p теңдеу түбірі немесе
ξp = p-1(p) = Q(p), 0 p 1;
ξ12 – үлестірім медианасы;
X([np]+1) – p ретінің таңдамалы квантилі, бұл жерде [np] np-дан аспайтын
бүтін санды білдіреді;
X([nλl]+1 – λl ретінің таңдамалы квантилі, 0 λ1 λ2 λ3 λk 1
Бірақ таңдамалы медиана бұл:
X(n+1)2 , егер n жұп болса;
(X(n2) + X(n2 +1)) , егер n тақ болса;
Ары қарай,
W, Wn = X(n) – X(1) – (таңдамалы) құлаш;
W(i) = Xn-i+1) – X(i) – i-ші квазиқұлаш (W(1) = W);
W, Wn,k – к құлаштың орташасы;
jW – j – ші таңдаманың құлашы;
Wrs = X(s) – X(r) ;
µ = EX, δ2 = DX – Х кездейсоқ шамасының математикалық күтімі және
дисперсиясы; µх = ЕХ, µy = EY - Х және У кездейсоқ шамаларының
математикалық күтімдері (екі өлшемді жағдай);
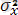
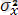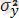
=Dx, 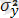Dy – X және Y кездейсоқ шамаларының дисперсиясы;
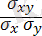
σху =cov(x,y),ρ = 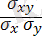– X,Y кездейсоқ шамаларының ковариациясы және Х,У
кездейсоқ шамаларының арасындағы корреляция коэффициенті;
µr:n = EXr:n – Xr:n кездейсоқ шамасының математикалық күтімі;
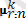
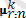– Xr:n кездейсоқ шамасының к-шы ретті моменті;
µrs:n = EXr:nXs:n
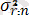
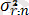= DXr:n; σrs:n = cov(Xr:n, Xs:n);
Q(x) = P-1(x) – P үлестірім функциясына кері функция;
Рr = r(n+1), qr = 1 – pr;
Qr = Q(pr), fr = p(Qr);
= ;
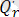
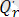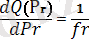
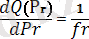Sν – еркіндік дәрежесі ν болатын σ үшін бағасы; N(µ,σ2) қалыпты үлестірім
үшін баға νS2νσ2~X2;
Qn,ν = WnSν – стьюденттелген құлаш (Wn және Sν тәуелсіз)
S = [Σ(Xi – X)2(n – 1)]12 – σ үшін баға (ішкі);
S(p) = {[(n -1)S2 + νS2ν] (n – 1) + ν)} – σ үшін суммалық баға;
jS – j – ші таңдама үшін S–ң мағынасы;
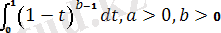
B(a,b) = 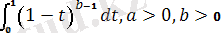бета – функция;
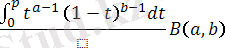
Ip(a,b) = 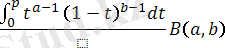толық емес бета – функция; (1.3.1)
B(a,b) – бета үлестірімі бар Х кездейсоқ шамасы Р(Х≤х) = Ix(a,b) үлестірім
функциясымен; (1.3.2)
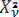
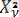- еркіндік дәрежесі ν болатын хи-квадрат үлестірімі Х кездейсоқ
шамасы;
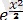
φ(х) = (2π)-12 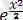– стандартты қалыпты заңдылықтың үлестірім тығыздығы,
∞∞;
N(µ, σ2) - µ математикалық күтім және σ2 дисперсиядан тұратын қалыпты
кездейсоқ шама;
N(µ, Σ) - µ математикалық күтім векторы мен Σ ковариациялық матрицадан
тұратын көп өлшемді қалыпты кездейсоқ шама;
n(k) = n(n-1) ... (n-k+1), k = 1,2, ..., n;
[x] – x – тің бүтін бөлігі (бірақ µ[k] = EXk);
X ~ N(µ, σ2) - µ математикалық күтім және σ2 дисперсиядан тұратын қалыпты
үлестірімі бар Х кездейсоқ шамасы( аналогты ұқсас белгілеулер басқа ықтимал
үлестірімдер бар кездейсоқ шамалар үшін қолданылады);
Ү.т(ф.п) – үлестірім тығыздығы;
Ү.ф(ф.р) – үлестірім функциясы;
Н.к.о – оценки наименьших квадратов(аз квадраттардың бағасы);
РНМ – равномерно наиболее мощный( біркелкі ең мықты);
ПХ – Пирсон және Хартли (1961) – Биометрикалық кестелер 1;
СГ – Сархан және Гринберг (1970) – реттік статистикалар теориясына кіріспе;
П.5.3 – 5.3.Қ – §5.3 – на қатысты кестелер тізімінен тұратын қосымша;
С.в – к.ш – кездейсоқ шама.

ІІ Тарау
Үлестірім теориясының негізі
§2.1 Реттік статистикалар үлестірімі

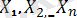
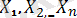– ортақ үлестірім функциясы бар n тәуелсіз кездейсоқ шамалар
деп алайық. Fr(x) (r = 1,2,..., n) r – ші реттік статистиканың үлестірімі
функциясы болсын. Онда ең үлкен реттік статистиканың үлестірім функциясы
мына формуламен беріледі:
Fn(x) = P{X(n) ≤ x} = P{барлық Хі х – тан аспайды} = Pn(x)
Бұған ұқсас мына формуланы аламыз:
F1(x) = P{X(1) ≤ x} = 1 – P{X(1) x} = 1 – P{барлық Xi x } = 1 –
[1 – P(x)]n (2.1.2)
Бұл формулалар Fr(x) – қа арналған келесі жалпы формула үшін маңызды дербес
жағдайлар:
Fr(x) = P{X(r) ≤ x} = P{ең болмағанда Xi -дегі r х – тен кіші немесе тең} =
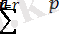
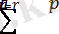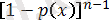
(x)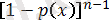, (2.1.3)
Бұл суммалардың оң жақ бөлігіндегі і – ші қосылым Х(1), X(2),..., X(n)
шамаларынан дәл і шама х – тен аз немесе тең болатындығының биномиальды
ықтималдығы болады. (2.1.3) – ті мына түрде жазып:
Fr(x) = Ep(x)(n,r)
(2.1.4)

E функциясы көптеген деректерде кестеленгенін байқаймыз(мысалы, E(n,r,
Р(х)) белгілеуі қолданылатын Гарвард есептеу лабораториясы(1955)). Сонымен
қатар, биномиалды сумма мен толық емес бета – функция арасындағы
арақатынастан
Fr(x) = Ip(x)(r, n – r + 1)
(2.1.5)

шығады, мұндағы Ip(a,b) (1.3.1) – де анықталған. Олай болса, Fr(x) Ip(a,b)
таблицалары бойынша шығарылуы мүмкін(К.Пирсон (1934)). X(r) проценттік
нүктелерін осы таблицалардан кері интерполяциялау арқылы немесе бірден
толық емес бета – функциялардың проценттік нүктелерін беретін
“16 Биометрикалық таблицалар” таблицасынан (Пирсон және Хартли (1966))
таблицасынан алуға болады.
Мысал 2.1
Стандартты қалыпты үлестірімнен таңдама көлемі 5 болатын X(4) жоғарғы
5 пайыздық нүктені табайық.
Ip(x)(4,2) = 0,95
немесе
I1-p(x)(2,4) = 0,05
арақатынасын қанағаттандыратын х – ті іздеп жатырмыз. Соңғы теңдіктен
1 – P(x) = 0,7644 шығады. Сол себепті x = 1,429.
(2.1.1) – (2.1.5) формулалары үзіліссіз және де дискретті шамалар үшін
де әділетті екенін байқау керек. Енді біз Xi - p(x) = P'(x) үлестірім
тығыздығы бар үзіліссіз шамалар деп ұйғаратын боламыз, бірақ біз §2.4 - гі
дискретті жағдайға ораламыз. Егер fr(x) – X(r) кездейсоқ шамасының
үлестірім тығыздығы болса, онда (2.1.5) - тен мына теңдік шығады:
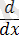
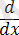
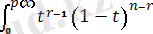
Fr(x) = 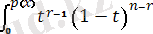dt = pr-1(x)[1 – P(x)]n-rp(x) (2,1.6)
Бұл формула маңыздылығы үшін біз оны басқа әдіспен тағы шығарамыз.
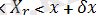
х 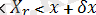оқиғасы келесі жолмен іске асуы мүмкін:

r - 1 1 n - r
x x + δx

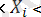
Xi ≤ x Xi шамасының ішінен r – 1 шама үшін, x 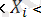x + δx Xi және
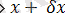
Xi 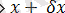екеуінің бірі үшін және Xi - дің қалған n – r шамасы үшін
n бақылауларды мынадай 3 топқа бөлу әдістерінің саны мынаған тең:

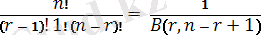
Және олардың әрқайсысында мынадай ықтималдық болады:
Pr-1(x)[P(x + δx) – P(x)][1 – P(x + δx)]n-r
Сондықтан, δх - ті аз деп есептеп, мынаны аламыз:
P{x≤ x + δx} = Pr-1(x)p(x)δx[1 – p(x + δx)]n-r + O(δx2),
Мұндағы O(δx2) - (δx2) ретінің мүшесін білдіреді және Xi – дің ең
болмағанда біреуі (x, x+ δx) интервалына түсетін x оқиғасының
орындалуының ықтималдығы өзіне қосады. Екі жақ бөлігін δх – ке бөліп және 0
– ге ұмтылдырсақ, қайтадан (2.1.6) – ны аламыз.

§2.2 Реттік статистикалардың екі немесе көп сандардың ортақ
үлестірімі

X(r) және X(s) - ң ортақ тығыздығын frs(x,y) арқылы белгілеген
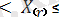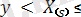
ыңғайлы. Егер құрама оқиға x x + δx, 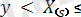y + δy мына конфигурация
түрінде іске асатынын байқасақ(дәлдікпен аз реті көп мүшелерге дейін)
(2.1.5) - ке лайық формуланы шығаруға болады:

r - 1 s – r - 1 1 n - s
x x + δx y + δy

Бұл барлық бақылаулардың ішінде (r - 1) x - тен кіші, біреуі (x, x + δx)
интервалына түседі және т.б. Бұл жерден x ≤ y үшін
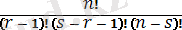
Frs(x,y) = 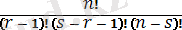Pr-1(x)p(x)[P(y) – P(x)]s-r-1p(y)[1 – P(y)]n-s
(2.2.1)
Енді (2.2.1) үшін жалпылау қалай көрінетіні түсінікті. , ,...,
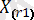
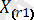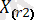
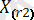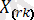
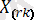(1 ≤ r1 ≤ n; 1 ≤ k ≤ n) шамаларының ортақ үлестірім тығыздығы
x1≤x2≤xk үшін мына түрде болады:
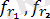
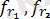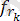
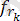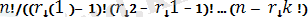
,...,(x1,x2,...,xk)=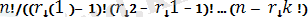х
хPr-1(x1)p(x1)[p(x2)–p(x1)p(x2)...[1– P(xk)p(xk)
(2.2.2)

Егер x0 = ∞, xk+1 = +∞, r0 = 0, rk+1 = n +1 екенін анықтасақ, онда (2.2.2)
-ң оң жағын мына түрде жазуға болады:
n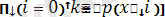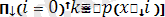![ (2.2.3)

Сонымен қатар барлық n реттік статистикалардың ортақ үлестірім тығыздығы
мынадай қарапайым түрге ие болады:
n! p(x1)p(x2) ... p(xn).
xi мағыналарын ретке келтірудің n! тең ықтималды тәсілдері бар
болғандықтан, соңғы нәтиже әрине айқын. Ол үзіліссіз жағдайдағы к реттік
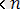
статистикалардың (k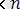) ортақ үлестірімін шығару үшін жіберілетін нүкте
ретінде қолданылуы мүмкін.
X(r) және X(s) Frs(x,y) ортақ үлестірім функциясы (2.2.1) - ді
интегралдау арқылы алуға болады, сондай ақ тікелей дәлелдеудің көмегімен,
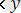
сонымен қатар жарамды және дискретті жағдай үшін x 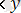үшін мынаны аламыз:

Frs(x,y) = P{ ең болмағанда Xi шамасынан r x – тен аспайды; Xi шамасынан s
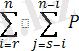
y – тен аспайды} = 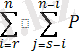{Хi шамасынан дәл i x – тан аспайды; xi шамасынан
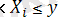
j x 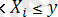теңсіздігін қанағаттандырады}.
Бұл теңсіздіктерде егер i s, онда j 0 – ден басталады деп
ұйғарылады. Олай болса, x y үшін мынананы аламыз:
Fr.s(x,y)=*Pi(x)[P(y)–P(x)]j * [1–P(y)]n-i-j
(2.2.4)
xүшін X(s) ≤ y теңсіздігінен X(r) ≤ x шығады, сол себепті Frs(x,y) =
Fs(y) (2.2.5)

§2.3 Құлаштың және басқа жүйелі статистикалардың үлестірімдері

k реттік статистикалардың ортақ үлестірім тығыздығын біле, біз
стандартты әдістермен реттік статистикалардың кез – келген жақсы
функциясының үлестірім тығыздығын шығара аламыз.Мысалы, Wrs = X(s) – X(r)
үлестірім тығыздығын табу үшін, (2.2.1) – ге wrs = y - x қоямыз, бұдан x,y
– ң x, wrs - ке өзгеруі 1 - ге тең якобианға ие болатынын байқаймыз. Олай
болса, Crs арқылы (2.2.1) – де тұрақтыларды белгілей отырып және х бойынша
интегралдасақ, мынаны аламыз:
F(wrs)=Crs(x)p(x)[P(x+wrs)–P(x)]s-r -1*p(x+wrs)[1–P(x+wrs)]n-sdx
(2.3.1)
Wrs W құлашы болатын r =1, s = n жағдайы ерекше назарға лайық және (2.3.1)
мына түрге ие болады:
f(w) = n(n – 1)[P(x + w) – P(x)]n-2p(x + w)dx
(2.3.2)
W шамасының үлестірім функциясының тағы бұдан қарапайым түрі бар.
Интегралдау ретін ауыстыра отырып, мынаны аламыз:
F(w) = nn-2dw’dx =
= nn-1 dx = nn-1dx (2.3.8)
np(x)dx[P(x + w) – P(x)]n-1 - тең болу ықтималдығы, Xi шамаларының дәл
бір белгілі x (x + dx) интервалында жатады, ал қалған (n – 1) - і (x, x
+ w) интервалына түсетінін байқай отырып, бұл маңызды нәтижені алуға
болады.
(2.3.1) – (2.3.3) формулаларын пайдаланғанда, х өзгеру облысы ақырлы болуы
мүмкін екенін ескеру керек.
Мысал.2.3.
Келесі жағдайда реттік статистикалардың үлестірімін және Wrs – ті табайық.

p(x) – теңөлшемді үлестірімдердің тығыздығы: p(x) = 1 (0 ≤ x ≤ 1), кері
жағдайда
p(x) = 0
(2.1.6) – дан дереу мынаны аламыз:

fr(x) =

Олай болса, (1.3.2) анықтамаға сәйкес, Xr бета β(r, n – r + 1) шама болып
табылады. (2.2.1) – ден

frs(x,y) =

x үшін p(x + wrs) = 0 болғандықтан (2.3.1) – ден

f(wrs) = Crs

x = y(1 – wrs) – ті қойып, мынаны аламыз:
f(wrs) = Crs (0 (2.3.4)
Бета үлестірімі бар s және r –дің әрқайсысынан емес, тек s -r –ден
ғана тәуелді екенін осы қарапайым нәтиже көрсетеді.
Құлаштан басқа қарапайым жүйелі статистикалар назарға алынады:
квазиқұлаштар Wr,n-r+1 (r = 2,3,...,), жұп n үшін тең таңдамалы медиана,
және экстремальды қатынастар. Соңғысы дұрыс жарты осьте берілген
үлестірімдер үшін анықталады.

§2.4 Дискретті үлестірім үшін реттік статистикалар

Егер p(x) x = 0,1,2,... нүктелерінде топталса(жинақталса), онда
fr(x) = P{X(r) = x} қоямыз. Соңғы функция X(r) шамасының ықтималдықты
функциясы деп (в.ф). Ол үшін (2.1.4) және (2.1.5) –тен мынаны аламыз:
fr(x) = Fr(x) – Fr(x-1) = Ep(x)(n,r) – Ep(x-1)(n,r) = Ip(x)(r,n-r+1) – Ip(x-
1)(r,n-r+1).
(2.4.1) frs(x,y) = Frs(x,y) – Frs(x-1,y) – Frs(x,y-1) + Frs(x-1, y-1),
x≤y
болғандықтан, frs(x,y) екі өлшемді ықтималдықты функция үшін теңдік (2.2.4)
және (2.2.5)-тен шығады: frs(x,y) = P(X(r)=x, X(s)=y)
Есептеу тұрғысынан қарағанда бұл теңдік ыңғайлы көрінгенмен,
Кхатриге(1962) тиісті теориялық жұмысқа пайдалы басқа теңдік (ұсыныс) бар.
Бізді (2.2.1)-ге алып келген пікірлердің көмегімен, үшін келтірілген типтік
конфигурацияға сәйкес мынаны аламыз:
Мұнда - барлық теріс емес бүтін u, t қосындысы, мұндағы u + t ‹ s – r
– 1
Crs = n![(r – 1)!(s – r – 1)!(n – s)!] белгілеп, мына теңдікті аламыз:

Қосынды және интеграл белгілерінің орындарын ауыстыра отырып және
ϑ = P(y) – z’P(y), w = P(x-1)+zP(x) қойсақ, онда мынаны аламыз:
. (2.4.2)
Егер x=y болса, онда ұқсас мынанаы аламыз:
(2.4.3)

Мұнда интегралдау облысы P(x-1) ≤ w ϑ ≤ P(x) бойынша жүргізіледі.
(2.4.2) – де w ϑ теңсіздігі автоматты түрде орындалғандықтан, ондабұл
жерден жалпы нәтиже шығады:
(2.4.4)

Мұнда интегралдау w ϑ облысы бойынша жүргізіледі, P(x-1) ≤ w ≤ P(x),
P(у-1) ≤ ϑ ≤ P(у)

§2.5 Квантиль үшін параметрсіз сенімділік интервалдар.

Х – қатаң өспелі Р(х) – үлестірім функциясының үзіліссіз шамасы деп
ұйғарайық. Онда Р(х) = p (0 (2.5.1) теңдеуінің жалғыз шешімі бар,
айталық х = p, оны біз р ретінің (бас) квантилі деп атаймыз. Олай
болса,
ξ12 – үлестірім медианасы. Егер р(х) қатаң өспелі болмаса, онда Р(х) = p
кейбір интервалда әділ болуы мүмкін. Бұл жағдайда бұл интервалдың кез –
келген нүктесі р ретінің квантилі қызметін атқара алады.
Х дискретті кездейсоқ шамасы үшін р квантилін келесіні
жалпылаудың көмегімен анықтауға болады:
P{X (2.5.2)

Бұл арақатынас р – ны жалғыз әдіспен анықтайды, егер тек Р р –
ға тең болмаса, кері жағдайда p тағы да кейбір интервалда жатады. Біз
енді егер Х үзіліссіз болса, онда кездейсоқ интервал (X(r), X(s)) –
ны Р(х) – тан емес, r,s,n және р – дан тәуелді ықтималдықпен жабатынын,
одан параметрсіз сенімді интервал шығатынын көрсетеміз. Осы мақсатпен
X(r)ξp оқиғасы бөлек құрама оқиғалардың бірігуіне тең: X(r)ξp,
X(s)ξp және X(r)ξp, X(s)ξp. Олай болса, X(s)ξp
теңсіздігінен X(r)ξp шығатындықтан, онда

P{ X(r)ξp} = P{ X(r)ξp X(s)} + P{ X(s)ξp}
немесе
P{ X(r)ξp X(s)} = P{ X(r)ξp} – P{ X(s)ξp}
(2.5.3)

Үзіліссіз жағдайда (X(r), X(s)) р – ны

теңдігіне тең болатын ықтималдықпен жабатыны (2.5.1), (2.1.5) және
(2.1.3) – тен шығады.
Бұл Томпсон(1936) бойынша алынған нәтижеге ұқсас, бізге міндеттелген
нәтиже болып табылады, тағы бір дәлел 2.5.1 жаттығуында көрсетілген.
Дискретті жағдайда P{ X(r)ξp}p және P{Xр}
теңсіздіктерінен мына теңсіздіктер шығады:
P{ X(r)ξp}(r, n-r+1), P{X(s)р}(s, n-s+1),
(2.5.5)
Сол себепті (2.5.3) – тен мына теңсіздік алынып тасталынады:
P{ X(r)ξp X(s)}(r, s, n, p).
(2.5.6)
Аналогтық ой жүгіртулердің(пайымдаулардың) көмегімен
P{ X(r)ξp X(s)}(r, s, n, p) теңсіздігін (2.5.7) аламыз.
(2.5.6) және (2.5.7) теңсіздіктерінің ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.