Қатты дене статикасы

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 52 бет
Таңдаулыға:

Жоспар:

Кіріспе . . . 3

І - бөлім. Қатты дене статикасы . . . 4

1. 1. Статиканың негізгі ұғымдары мен аксиомалары . . . 4

1. 2. Байланыс және байланыс реакциялары . . . 6

1. 3. Жинақталған күштер жүйесі . . . 8

1. 4. Параллель күштері жүйесі . . . 4

1. 5. Күштердің кез келген жазық системасы . . . 6

1. 6. С-1 есебі . . . 8

1. 7. С-4 есебі . . . 9

ІІ - бөлім. Қатты дене кинематикасы . . . 10

2. 1. Қатты дененің ілгерілмелі қозғалысы . . . 10

2. 2. Қатты дененің тұрақты өсті айнала қозғалысы . . . 14

2. 3. К-2 есебі . . . 18

2. 4. Қатты дененің жазық параллель қозғалысы . . . 21

2. 5. Еркін қатты дене қозғалысы . . . 25

ІІІ - бөлім. Материялық нүкте динамикасы . . . 27

3. 1. Ньютон заңдары . . . 27

3. 2. Материялық нүкте динамикасының негізгі теоремалары . . . 30

3. 3. Д-2 есебі . . . 31

3. 4. Материялық нүктенің салыстырмалы қозғалысы . . . 35

3. 5. Материялық нүктенің салыстырмалы қозғалысының дифференциялық теңдеулері. Инерция күштері . . . 38

3. 6. Инерция күштерінің физикалық мағынасы. Классикалық механиканың салыстырмалы принципі . . . 40

Қорытынды . . . 50

Кіріспе

Мен осы курстық жұмысымда теориялық механиканың статика, кинематика, динамика бөлімдеріне тоқталдым.

Теориялық механика - материялық денелердің механикалық қозғалысының жалпы заңдылықтары, мен тепе - теңдігін және осы материялық денелердің өзара механикалық әсерлесуін зерттейтін ғылым. Өзара механикалық әсерлесу нәтижесінде бір материялық денелер басқа материялық денеге қарағанда қозғалысқа келтіріледі, яғни материялық денелер өзінің бастапқы қалпын өзгертеді (деформацияланады) немесе жоғарыда аталған екі жағдай қатар байқалады.

Осы курстық жұмыстың негізгі мақсаты - қазіргі кезеңде отандық машина жасау өндірісін дамыту, жаңа өндірістік технологияларды халық шаруашылығына енгізу, космос кеңістігін игеру және тағы басқа техникалық шешімдерді анықтауды қажет ететін күрделі мәселелер механика ғылымының қарыштап дамуына өзінің ықпалын тигізетіні сөзсіз.

Теориялық механика пәні статика, кинематика және динамика деп аталатын үш бөлімнен тұрады.

Статика теориялық механиканың күштер (күштер жүйесі) түуралы ілім баяндалатын және осы күштер әсер еткендегі материялық денелердің салыстырмалы тепе - теңдік шарттары мен теңдеулері зерттелетін бөлім.

Егер дене басқа денелермен салыстырғанда тыныштық күйде болса, онда дене тепе - теңдікте болады деп айтуға болады. Дененің тепе - теңдік шарты дененің күйіне байланысты. Сұйық және газ тәрізді денелердің тепе - теңдігі гидростатика және аэростатика пәндерінде қарастырылады.

Кинематика деп материялық денелер озғалысының геометриялық сипаттамаларын (траекториясын, үдеуін, жылдамдығын), зерттйтін теориялық механика тарауын айтады. Осы зерттеулерде денелердің инерттілігі (массасы) және оларға әсер ететін күштер есепке алынбайды. Сондықтан да кинематиканы қозғалыс геометриясы деп те кейде оны «төрт өлшемді гещметрия» деп те, атайды. Өйткені Ньютон механикасында, яғни қазіргі кезеңдегі теориялық механиканың негізі болып саналатын классикалық механика да, материя (материялық дене) орын ауыстыратын кеңістіктің қасиеттері үш өлшемді эвклидтік кеңістіктің аксиомалары мен теоремаларына тәуелді болады да, ал төртінші өлшем ретінде дәл кеңістік сияқты материяға тәуелсіз, абсолютті шама - уақыт алынады.

Динамика бөлімінде материялық нүктенің, қатты дененің қозғалысы зерттелгенде, осы қозғалыстың себебі болатын әсер етуші күштер және материялық обьектілердің инерттілігі (масса) ескеріледі.

Осы курстық жұмыс арқылы теориялық механиканың әр түрлі өнеркәсіптердің негізі бола алатын ғылым ретінде таныдым.

1. 1. Статиканың негізгі ұғымдары мен аксиомалары

Статика деген гректiң statike деген сөэiнен шыққан. Грекше бұл бір орында тұру қозғалмау, тыныштықта болу деген сияқты ұғымдарды бiлдiредi. Статика - күш әсерiнiдегi материялық денелердiң тепе теңдiгiн зерттейтiн ғылым. Баяндау тәсiлiне орай ол геометриялық және аналитикалық статика болып ек түрге бөлiнедi. Аналитикалық статикада механикалық системаның ең жалпы тепе-теңдiк шарттары тағайындалады. Мұнда зерттеулер таза аналитикалық тәсiлмсн жүргi зiледi. Аналитикалық статиканың қорытындылары кез келген мехакикалык система үшiн дұрыс болады. Бұл статиканы кейiнрек қарастырамыз. Геометриялық статикада абсолют қатты денелердiң өзiне түсiрілген күштер әсерiнен болатын тепе-теңдiгi жөнiндегi мәселелер қарастырылады. Ондай мәселелердiң өзi екiге бөлiнедi: 1) абсолют қат ты денега әсер ететiн күштер системасын қарапайым түрге келтіру;

2) абсолют қатты денеге әсер ететiн күштер системасының тепе-теңдiк шарттарын тағайындау. Осыдан барып статиканы қысқаша күштер туралы ғылым дейтiн ұғым туады.

Денелердiң қозғалыста, не тыныштықта болуы, бiрiншiден, ол денелерге қандай күштер әсер ететiнiне екiншiден, дененің орны қандай санақ системасына қатысты қарастырылатындығына байланысты. «Қозғалыс» және «тыныштық» дегеніміз салыстырмалы ұғымдар. Олар туралы сөз болғанда алдымен қандай да санақ системасын тағайындап алуымыз қажет. Сөйтiп, алдын ала санақ системасы және күш туралы ұғымдарға тоқтап өтуiмiз керек.

1. 1. Санақ системасы. Координаталық осьтер системасы. Денелердi кеңiстiктегi орны қозғалмайды деп алынған қандай да бір денеге (немесе бiр-бiрiмен салыстырғанда қозғалмайтын бір топ денеге) қатысты анықталады. Осы денемен салыстыра отырып берiлген дененiц орын ауыстыруын есептеп шығарамыз. Мысалы, бiзге берілгенi В денесі болсын. Оның кеңiстiктегi орнын қозғалмайды деп алынған екiншi бiр А денесiмен салыстыра отырып анықтайық (1. 1-сурет) .

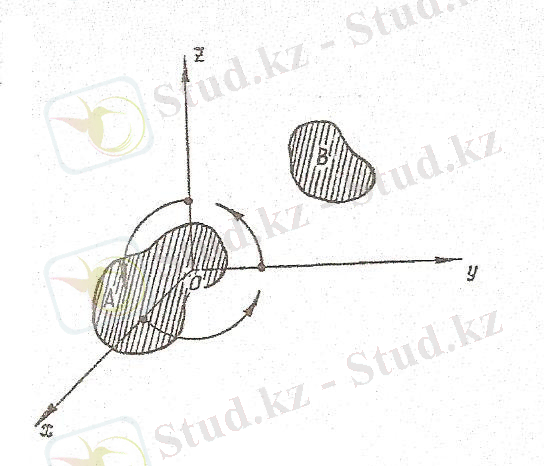1. 1-сурет

Өзiне қарағанда басқа денелердің орны, қозғалыс күйі салыстыру арқылы анықталатын, қозғалмайды деп алынған осы А денесi санақ системасы деп аталады. Сонымен, берiлген денелер қозғалысын әрбiр жолы белгілі бiр санақ системасымен салыстырып қарастыруымыз керек. Түрлi жағдайларда санақ системасын түрліше тәсiлмен сайлап алуға болады. Практикада қозғалысты сипаттау үшiн санақ системасын құрайтын денелерге қандай да бiр коорданаталар осьтерiнің системасын байланыстырады. Теориялық механикада көбiне х, у, z координаталарының тік бұрышты декарттық системасы қолданылады (1. 1-сурет) . Бұдан былай үнемi тек оң системаны пайдаланатын боламыз. Бұл система үшiн оң бұрғы ережесi қолданылады. оz осiнiң оң ұшынан қарағанда ох осінің оz осiне қарай ең аз бұрышқа бұрылысы сағат тiлiне айналысына керi бағытта көрiнуi керек, сол сияқты ох ұшынан қарағанда оу-тiң оz-ке карай, ал оу-тің ұшынан қарағанда оz-тiң ох-ке қарай айналыстары дәл осылай болуы қажет.

Сонымеа, осыдан әрi қарай В-ның немесе басқа денелердiң тепе-теңдiгi, не қозғалысы алдын ала алынған қандай да бiр охуz осьтер системасына қатысты зерттелiнедi. А денесi қозғалмайтын дене ретiнде алынғандықтан, онымен байланыстырылып алыған охуz осьтер системасын да қозғалмайтын немесе абсолюттiк система деп есептеймiз. Сөйтiп, статикада инерция заңы орындалатын координаталық осьтер системасы алынады.

1. 2. Негiзгi анықтамалар. Геометриялық статикада тек қана абсолют қатты дене тепе-теңдiгi қарастырылады. Сол себептi осыдан былайғы жерде күштердi тек абсолют қатты денеге түсiрiлген күштер ден есептейтiн боламыз. Алдағы уақытта айтуға жеңiл болу үшiн абсолют қатты дене деп жатпай тек қатты дене дейміз.

Бұдан былай еркiн қатты дена ұғымын жкi қолданамыз. Еркiн дене деп басқа денелермен ешбiр байланысы жоқ, ешнәрсемен де бекiтiлмеген дененi айтамыз. Ол дена кеңiстiктiң кез келген орнында бола алады және кез келген бағытта орын ауыстыра алады.

Қатты деаеге бір ғана күш емес бiрнеше күш әсер етуi мүмкін.

Оларды деп белгiлейік.

Қандайда болмасын бiр қатты денеге әсер ететiн күштер жиынын

күштердiң системасы деп атайды.

Қандай да боамасын () -n күштiң системасын тыныштықта тұрған еркiн қатты денеге түсiргенде ол оған ешқандай қозғалыс бере алмайтын болса, онда бұл күштердiң системасы тепе-теңдiктегi система деп немесе нольге эквивалент деп аталады:

() ∞0

Басқаша айтқанда, системадағы күштер бірiнiң жасайтын әсерiн бiрi

жойып, натижесiнде күшттердiң бұл системасы тыныштықтағы еркiн

дененi ешқандай да қозғалысқа келтiре алмайтын болады. Егер еркін дене осыған дейiн қозғалыста болса, онда күштердiң мұндай системасы оған ешқандай да өзгерiс жасай алмайды. Қозғалыстың бағыты да, жылдамдықтары да өзгермей қала бередi.

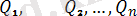
Егер () және ( 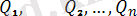) күштердің екi системасының әрқайсысы бір еркiн қатты дененi тыныштықтағы күйiнен бiрдей бiр қозғалысқа келтiретін болса, онда бұларды бiр-бiрiне эквивалент системалар деп атаймыз. Бұл анықтаманы былай жазамыз:

() ∞ ( )

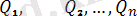
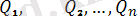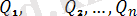
Осы анықтаманы былайша толық тусiндiруге болады. Егер () системасы бiр қатты дене D-ға әсер еткенде оны қандай қозғалысқа түсiрсе, не оны тыныштықта ұстаса, оған эквивалент екiнші бiр күштер ( 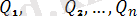) системасы да D денесiн дәл сондай қозғалысқа келтiредi немесе ол да D-ны тыныштықта ұстайды. Қысқаша айтқанда, эквивалент екi системаның бiр денеге жасайтын әсерлерi бірдей болады. Сол себептi мұндай екi күштер системасының бiрін екiншiсiмен алмастыруға болады.

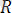
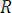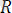
Қатты денеге түсiрiлген () күштерiнiң системасы бір күшке эквивалент болса, онда 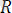күшін бұл күшiтер системасының тең әсер етушiсі немесе тең әсерлi күшi деп атайды. Сонда осы анықтаманы былай жазуға болады:

() ∞

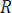
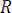
Егер қатты денеге әсер етушi барлық куштер жиыны тепе-теңдiкте тұрған күштердiң системасын құратын, яғни

() ∞ 0

болса, онда бұл дененiң өэi де тепе-теңдікте болады делiнедi.

Механикаға негiз болатын - Галилей-Ньютонның жалпы заңдары. Механиканың бұл жалпы заңдарына динамикада тоқталамыз. Бұл жерде статика негiзiне алынатын аксиомаларды баяндаймыз. Статика аксиомалары Галилей-Ныотонның жалпы заңдарынан туады. Олар механикаға толығынан негiз бола алмайды, бiрақ ол статикада қарастырылатын барлық мәселелердi қорытып шығаруга әбден жеткілікті.

1-аксиома (екi күштің тепе теңдік шарты туралы) . Сан мәндерi тең бір түзудiң бойы мен қарама-қарсы бағытталған еркiн қатты денеге әсер етушi екi күш өзара теңеседi немесе нөлге баламалы (1. 2-сурет) .

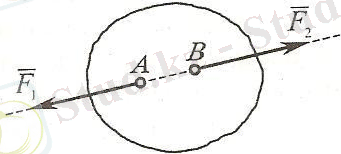1. 2-сурет

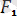
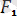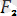
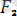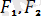
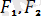= - , ( ) <=> 0.

Бұл аксиома теңескен күштер жүйесiн анықтайды.

2-аксиома (күштер жүйесiн түрлендiру туралы) . Өзара теңескен күштер жүйесiн қосқаннан немесе алып тастағаннан берiлген күштер жүйесiнiң қатты денеге әсерi өзгермейдi (1. 3-сурет) .

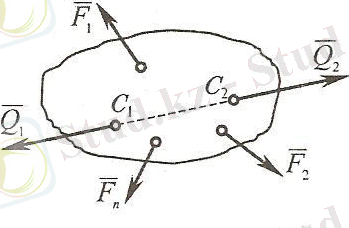1. 3-сурет

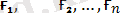
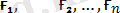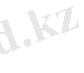
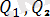
Алғашқыда қатты денеге( ) күштер жүйесi түсірілген болсын. Ендi денеге түзуiнiң бойымен қарама-қарсы бағытталған шамалары тең күштерін түсiрейiк, яғни ( 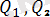) ˂=> 0.

Олай болса, ( ) ˂=> ( ) .

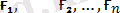
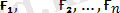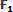
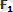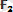
3-аксиома (күштер параллелограмының заңы) . Дененiң бiр нүктесiне түсiрiлген екi жане 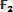күштерiнiң тең әсер етушi күшi сол нүктеге түсiрiледi де, осы күштерден тұрғызылған параллелограмның диагоналiмен анықталады (1. 4, а-сурет) .

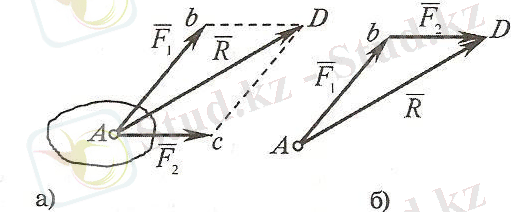1. 4-сурет

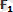
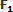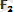
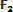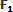
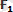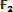
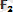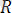
Осы және күштерiнің тең әсер етушi күшін параллелограмм тұрғызбай-ақ анықтауға болады. Ол үшін бiрiншi векторының ұшынан (1. 4, б-сурет) векторын жүргiземiз. Осы сынық сызықтың бастапқы және соңғы нүктелерін қосатын 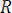векторы екi күштiң тең әсер етушi күшiн бейнелейдi. Екi күштiң тең әсер етушi күшін осындай әдiспен анықтайтын тәсiл, күштер үшбұрышының ережесi деп аталады.

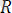
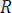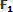
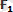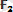
Векторларды қосу ережесi бойынша тең әсерлi күш = + 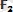, яғни күштердiң векторлық немесе геометриялық қосындысына тең болады. Тең әсер етушi күштiң модулi:

R =

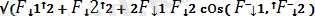
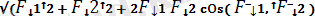
4-аксиома (әсер және керi әсер туралы заңы) . Екi дененiң бір-бірiне әсер ету күштерi шамасы жағынан тең және бір түзу бойымен қарама-қарсы бағытталады (1. 5-сурет) .

Бұл заң бойынша әрбiр әсерге оған тең және қарама-қарсы бағытталған керi әсер болады.

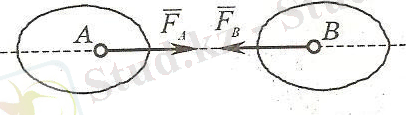1. 5-сурет

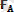
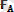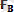
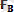және күштерi әр түрлi денеге түсiрiлген, сондықтан осы күштер тепе-теңдікте болатын күштер жүйесiн құра алмайды, яғни

( ) ˂≠>0.

Осы аксиомадан әлемде куштiң бiр жақты ғана әсерi болмайтынын көремiз.

5-аксиома (қатаю принципi) . Егер қатты емес дене теп-теңдiкте болса, онда ол қатты денеге айналғанда тепе-теңдiк шарты бұзылмайды.

Қатаю принципi қатты емес дене мен кез келген өзгермелi құрылмаларға (конструкцияларға) статиканың тепе-теңдiк шарттары қолдануға мүмкіндiк бередi. Осы шартты қатты емес денелердiң тепе-теңдiгiнің қажеттi шарттары деп алуға болады. Мысалы иiлмелi жiп тепе-теңдiкте болу үшiн оның екi ұшына әсер ететiн күштердiң шамалары бiрiне-бiрi тең және қарама-қарсы бағытталғаны жеткiлiксiз болады, себебi оған қосымша осы күштер жiптi созуы қажет.

1. 2. Байланыстар. Байланыстар реакциялары

Еркiн және еркiн емес дене. Кеңiстiкте кез келген бағытта қозғалыс жасай алатын дененi еркiн дене деп атайды. Егерде дене кейбiр бағыттарда қозғалыс жасай алмайтын болса, онда ол еркiн емес дене деп аталады. Дене қозғалысының еркiндiлігiн шектейтiн шарттарды механикада байланыстар деп атауға келiсiлген. Байланыстар туралы ұғым-механикадағы күрделi ұғымдардың бiрi. Оны толық түрде динамикада қарастырамыз. Статикада қарастырылатын байланыстар көбiнесе қозғалмайтын қатты дене, жiп, стержень, материялық нүкте түрінде кездеседi.

Мысалы, О нүктесiне жiппен iлiнген В жүгi (1. 6-сурет) еркiн емес (ерiксiз) дене болып табылады.

1. 6-сурет

Себебi В дене төмен қарай қозғала алмайды. Ол бағыттағы қозғалысты шектеп тұрган-АО жiбi. ОА жібi В жүгіне жасалған байланыс болады.

Байланыс рөлiн атқаратын дене берiлген, қозғалысы зерттелетiн денеге бір күшпен әсер етiп, оның қозғалысын шектейдi. Бұл күштi байланыс реакциясы дейдi. Байланыс реакциясьг байланысты ойша алып тастаған кездегi мүмкiн болатын дене қозғалысының бағытына қарам а-қарсы бағытталады.

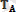
Бiздiң мысалда (1. 6-суретте) байланыс ретiндегi ОА жiбi берiлген В денесінің А нүктесiне түсiрiлген 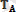реакциясын бередi. Ол жiп бойымен жоғары қарай бағытталады.

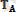
Егер жiптi ойша алып тастаған болсақ В жүгi ауырлық күшiнiң әсерiнен тік төмен қозғалар едi. Сондықтан 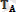реакция ол қозғалысқа қарама-қарсы жоғары бағыттал ады.

Байланыс реакциясы әруақытта берілген денеге түсiрiледi. Ал бұл күш дененi тепе-теңдiк күйiнен қозғалысқа келтiре алмайды. Дененi өздiгiнен қозғалысқа келтiре алмайтын, тек оның кейбiр бағыттағы мүмкiн болатын қозғалыстарына кедергi жасайтын байланыс реакциясын пассив күш деп атайды.

Тепе-теңдiгi (не қозғалысы) қарастырылып отырған денеге, байланыс реакцияларынан басқа да байланысқа тәуелсiз болатын, күштер әсер етедi. Мұндай күштердi актив күштер немесе берілген күштер деп атаймыз. Әрбір актив күштің модулі мен бағыты алдын ала берілген және денеге әсер етуші басқа күштерге тәуелсіз болады. Актив күштердің тағы бір ерекшілігі - оның тыныштықтағы денені қандай да бір қозғалысқа келтіре алатындығында.

Байланыстар реакцияларының сан шамалары мен бағыттары көп жағдайда алдын ала белгісіз және денеге әсер етуші актив күштер мен дененің қозғалысына тәуелді боады. Оларды берілген күштер мен байланыстар қасиеттеріне сәйкес тәуелділікте табу қажеттіліктігі туады. Мәселе еркін денеге әсер етуші күштер тепе-теңдігін қарастыруға келіп тіреледі. Оны еркін емес денелерге қолдануда байланыстар аксиомасына сүйенеміз.

Берілген денені оның қандай мақсатқа қолданылатынына қарай түрліше байланыстармен бекітеді. Статика мәселелерінде жиі кездесетін байланыстарды негізгі төрт типке бөлуге болады.

а. Денелердің өзара түйісуі

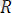
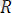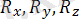
1) Жылтыр бет. Бірінші жуықтауда үйкелісін елемеуге болатын бетті жылтыр бет дейміз. Идеал жылтыр беттің реакциясы әр уақытта да жанасушы беттерге ортақ нормаль бойымен бағытталады. (1. 7. а, б, в-сурет) . Бұл және бұдан былайғы суреттерде А - берілген денені, В - байланысты, - байланыс реакциясын, 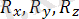- байланыс реакциясының координаталар осьтеріндегі проекцияларын көрсететін болады.

2) Жылтыр қисық. Идеал жылтыр қисық сызықтың реакциясы жанасу нүктесіндегі қисық нормалының бойымен бағытталады(1. 8. а, б-сурет)

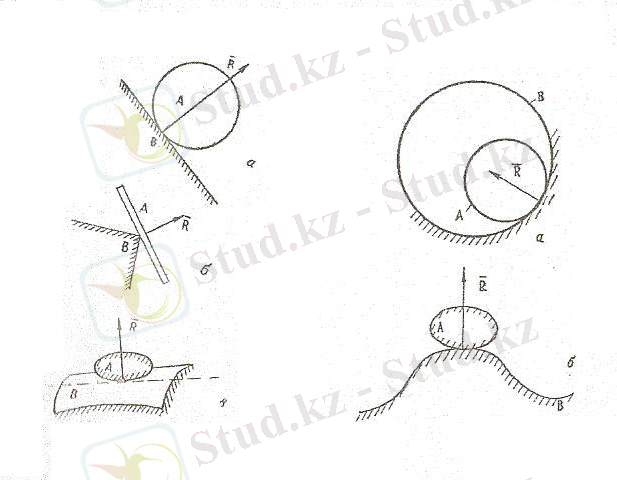
1. 7-сурет 1. 8-сурет

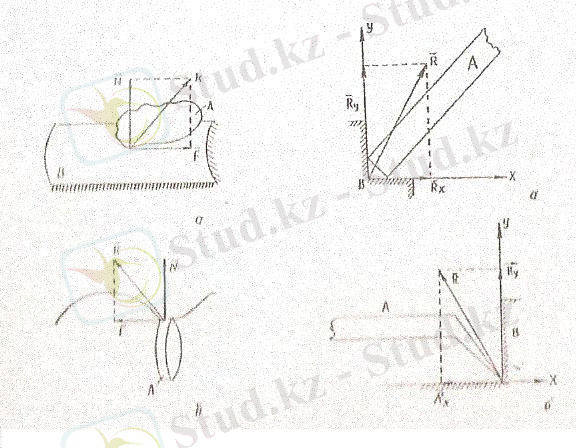
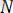
3) Кедір-бұдырлы бет. Егерде жанасушы денелердің беттері кедір-бұдырлы болса, онда байланыс реакциясы екі құраушыдан тұрады: оның біреуі ортақ нормаль, ал екіншісі ортақ жанама бойымен бағытталады. 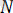нормаль бойымен бағытталғанын нормаль реакция деп, жанама бойымен бағытталғанын үйкеліс күші деп атайды. (1. 9. а, б-сурет)

4) Бұрыш. Егер дене бұрышқа тірелсе, онда дененің екі бағыттағы қозғалысына кедергі туады. Сол себепті бұрыштың реакциясы екі құраушыға жіктеледі. (1. 10. а, б-сурет)

1. 9-сурет 1. 10-сурет

б) Денелерді шарнирлер байланыстыру.

1) Жылжыиалы шарнирлер. Жылжыиалы шарнирлер дененің тіреу жазықтығымен қозғалыс жасауына кедергі келтірмейді де оған перпендикуляр бағыттағы қозғалысын шектейді. Сол себепті оның реакциясы әр уақытта тіреу жазықтығына перпендикуляр бағытталады. (1. 11. а, б, в-сурет)

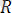
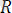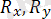
2) Жылжымайтын цилиндірлік шарнир. Цилиндрлік шарнирдің осі бойымен дене сырғып қозғала алады. Сондықтан да цилиндрлік шарнир реакциясы шарнир осіне перпендикуляр жазықтықта жатады (1. 12. а, б -сурет) . реакциясының бұл жазықтықтағы бағыты белгісіз. Сондықтан да ол өзінің 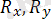проекциялары арқылы ізделінеді.

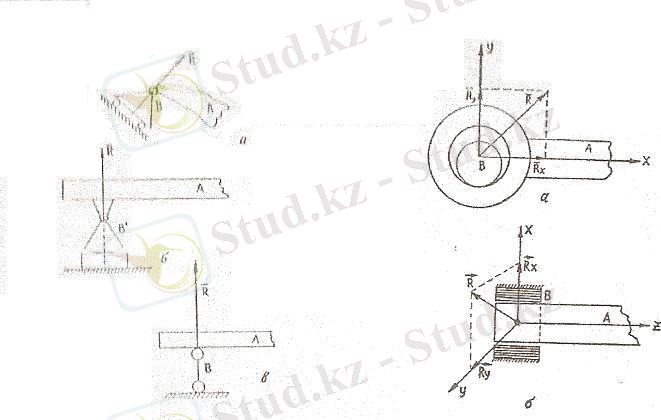
1. 11-сурет 1. 12-сурет

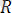
3) Жылжымайтын сфералық шарнир. Сфералық шарнир дененің бір нүртесін қозғалмайтын етіп бекітеді. Дене осы бекітілген нүктесі арқылы өтетін осьтен айнала алады. Қозғалмайтын нүктедегі реакция кеңістікте кез келген бағытта болуы мүмкін. Бағыты да, шамасы да белгісіз, толық 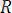реакциясының орнына әдеттеоның координаталық осьтердегі проекциялары ізделінеді (1. 13. а, б-сурет) .

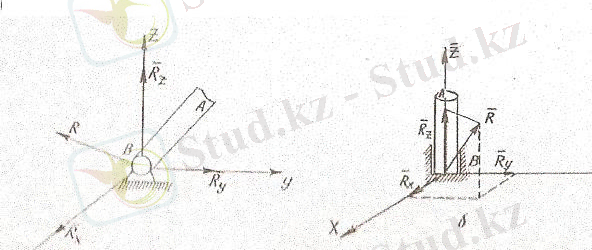
1. 13-сурет

в) Иілгіш байланыстар және стерженьдік байланыстар.

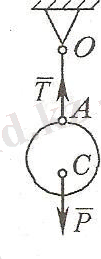
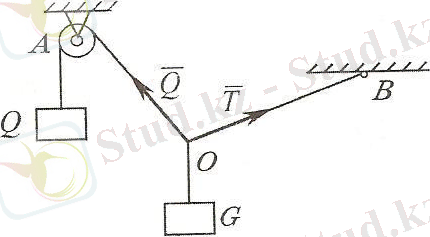
1) Жіп. Созылмайтын, иілгіш жіп түрінде берілген байланыс дененің бір ғана бағыттағы (жіп бойымен болатын) қозғалысын шектейді, яғни иілгіш байланыстар тек қана созылатын болады. Сондықтан да жіп реакциясы әр уақытта жіптің бойымен ол ілінген нүктеге қарай бағытталады (1. 14. а, б-сурет)

а б

1. 14-сурет

2) Стерженьдік байланыстар. Стерженьдік байланыстар салмақсыз, ұштары шарнирлермен бекітілген стерженьдер арқылы беріледі. Иілгіш байланыстарға қарағанда стерженьдер дененің екі бағыттағы қозғлысына кедергі жасайды. Стерженьдер берілген күштер әсерлерінен созылуға не сығылуға қарсы жұмыс істейді.

Стерженьдік байланыстар реакциясы стерженьдер осьтерінің бойымен немесе стержень ұштарындағы шарнирлерді қосатын сызықтың бойымен бағытталады (1. 15. а, б-сурет)

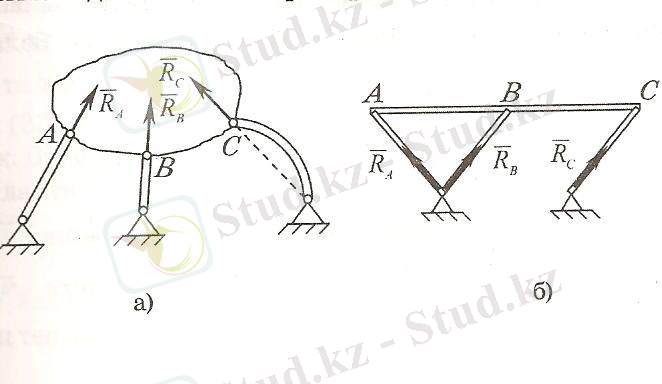
1. 15-сурет

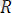
г) Қозғалмастай етіп қадалған денелер. Кейбір жағдайларда балғаның бір ұшы қабырғаға немесе еденге қазықша қадай бекітіледі. Бұл бекітуді - қадалған үш (заделка) деп атаймыз. Қозғалмайтын шарнирге қарағанда байланыстың мұндай түрі денеге тағы да бір кедергі жасайды. Ол берілген дененің байланысқа қарағандағы айналысын болдырмайды. Сондықтан да 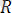реакциясымен бірге реакциялық момент те әсер етеді.

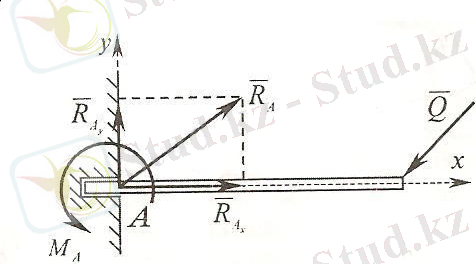1. 16-сурет

1. 3 Жинақталатын күштер системасы

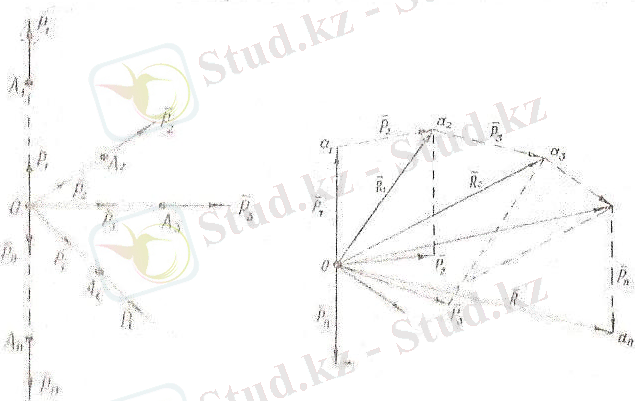
Жинақталған күштер системасының тең әсер етуші күші. Күштер көпбұрышы. Абсолют қатты дененің нүктелеріне, әсер ету сызықтары бір О нүктесінде қиылысатын, күштер түсірілсін дейік (1. 17-сурет) .

Мұндай күштер жинағы жинақталған күштер системасы деп аталатындығын айтқан болатынбыз. Жинақталған күштер системасы бір күшке эквивалент, яғни оның әр уақытта да тең әсер етуші күші болады. Тең әсер етуші күш системадағы күштердің геометриялық қосындысына тең болады да, оның әсер ету сызығы күштер түзулерінің қиылысушы О нүктесінен өтеді.

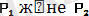
Осы айтылған ұйғарымды дәлелдеу үшін суреттегі күштердің бас нүктелерін күштер әсер ететін түзулер бойымен сырғыта отырып нүктелерінен О нүктесіне келтіреміз. Сонда жинақталатын күштер системасы бір нүктеге түсірілген күштер системасына келтіріледі, О нүктесіне түсірілген күштерге біртіндеп күштер параллелограмының заңын қолданамыз. 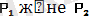күштерінің тең әсер етуші күші бұл заң бойынша осылардың қосындысына тең:

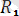
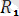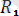
Одан кейін және күштер параллелограмм құру арқылы күшін табамыз (1. 18-сурет)

1. 17-сурет 1. 18-сурет

= .

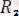
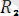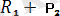
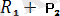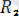
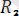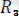
Келесіде және күштерінен параллелограмм құрамыз да 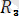күшін табамыз:

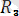
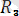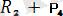
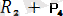
немесе

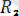
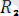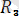
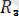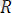
күші - күштерінің тең әсер етушісі. Осы ретпен соңғы күшіне дейін жеткіземіз. Бұл соңғы күшті алдыңғы n-l күштердің тең әсер етуші күшімен параллелограмм заңы бойынша қоссақ, системаның тең әсер етуші 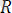күшін аламыз:

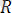
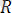немесе

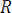
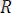= + . . . + = (1. 1)

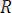
1. 18-суреттен 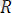тең әсер етуші күшін табу оның соңғы нүктесін табумен бірдей екенін көреміз. Ол үшін нүктелерін кезекпен саламыз. Сонда бұл нүктелер күштер көпбұрышының төбелерінде жатады да, ал оның қабырғалары сәйкес алынған күштерге тең болады.