Нүктелердің геометриялық орны әдісі

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 72 бет
Таңдаулыға:

Мазмұны

Кіріспе3

I тарау. Геометрия курсындағы салу есептері5

1. 1. Геометриялық салулар тарихынан5

1. 2. Конструктивтік геометрияның ортақ аксиомалары9

1. 3 Құралдар аксиомасы12

1. 4 Элементар салулар14

I I тарау. Салу есептерін шешудің негізгі әдістері23

2. 1. Салу есептерін шешудің геометриялық орындар әдісі және нүктелердің геометриялық орнын табу23

- Түзету әдісі және нүктелердің геометриялық орны31

2. 2Геометриялық түрлендірулер әдісі33

- Симметрия әдісі34

- Параллель көшіру әдісі36

- Айналдыру әдісі40

- Гомотетия әдісі42

2. 3. Салу есептерін шешудің алгебралық әдісі46

III тарау. Мектеп курс геометриясындағы салу есептерін51

3. 1. Мектептегі геометрия курсындағы оқулықтарды тақырып51

3. 2. « Геометриялық салу есептері» тақырыбы бойынша57

Педагогикалық тәжірибе61

Қорытынды65

Қолданылған әдебиеттер тізімі66

Қосымша материалдар68

Кіріспе

Салу есептері оқушылардың геометриялық есептеулерін толығымен қалыптастырудың маңызды құралы болып табылады. Геометриялық салуларды орындау процесі кезінде оқушылар геометриялық фигуралар және олардың арасындағы қатынастар қасиеттерімен танысады, сызбалық құралдарды қолдануды үйренеді, графикалық дағдыларды қалыптастырады. Көптеген математикалық тұжырымдардың дұрыстығына оқушылар көптеген жағдайда геометриялық салулар процесінде көз жеткізеді.

Қазіргі уақытта геометриялық салу есептері кейбіреулерге қызықсық, қажетсіз, ойдан шығарылған болып көрінуі де мүмкін. Циркуль мен сызғышты пайдаланып дұрыс он жетібұрышты көпбұрыш салу, үш биіктігі бойынша үшбұрыш салу немесе берілген түзуге параллель түзу салу не үшін қажет?.

Қазіргіт заман техникасы бұл салуларды кез келген адамнан әлде қайда тез, әлі дәлірек орындау мүмкіндігін, сонымен қатар, циркуль мен сызғышты қолданып шешуге мүмкін емес салу есептерін шешу мүмкіндігін туғызып отыр. Солай бола тұрса да салу есептерінсіз геометрия, геометрия болудан қалады. Геометрияны шын мәнінде жақсы сезіну үшін, оны жақсы көріп, ұнату үшін, салу есептерін айналып өтуге болмайды.

Берілген жұмыста сызбалық құралдар көмегімен салулардың іскерліктері мен дағдыларын қалыптастыруға арналған тапсырмалар жүйесінің сапасы жөнінде мәселе қарастыралады. Дәл осы іскерліктер оқушының жазықтықта ойлауын дамыту үшін шешуші болып табылатын мәселелер соңғы жарты ғасырдың көптеген психологиялық зертеулерінде дәлелденген. Бірақ әліде көптеген оқытушылар салу есептерін бағалай алмайды. Олардың көбісі, оқушылардың жазықтықта ойлауын дамыту үшін геометриялық обьектілердің көрнекілік модельдерімен қолдану керек деп ұйғарады. Шынында, психологиялық және педагогикалық зерттелер көрсеткендей, көрнекілік бейнелер жазықтықта ойлаудың дамуына көмектеседі, бірақ оқытудың бастапқы сатыларында ғана. Одан әрі ол, керісінше, бұл дамуды тежеуі мүмкін, өйткені оқушылардың өздеріне заттың геометриялық формасын көруі, оны түрлендіру мақсатымен осы формамен амалдар жасауы талап етілмейді.

Геометриялық салулар тек математикада ғана үлкен мағынаға ие болып қоймай, срнымен қатар оқушылардың математикалық дайындықтарын жүзеге асыруда да қатысы бар. Есептің ешқандай түрі салу есептері сияқты оқушылардың математикалық талабын және логикалық дағдыларын дамыту үшін мұншама көп материал бере алмайды. Салуға арналған есептер мектеп курсы геометриясының кез келген бөлімі бойынша теориялық білімін бекітуге ыңғайлы. Жазықтықта ой - өрісінің даму есептерін шешу үшін әдістемелік қалыптастыру және транзитивті құралған байланысты қолдану қажет:

▪ салуға тапсырма;

▪ жазықтықта ой - өрісін дамыту;

▪ оқушының математикалық дамуы.

Осындай транзитивті байланыстың әсерін қолдануда психологиялық және әдістемелік зерттеулерге қарағанда оқушылардың математикалық қабілеттерін дамытудағы салу есептері талас тудырмайтын роль атқарады.

Дипломдық жұмыстың мақсаты - 7- 9 сыныптардағы салу есептерін оқыту әдістемесін жасау.

Зерттеу пәні - салу есептерін оқыту әдістемесі

Зерттеу обьектісі - салу есептерінің элементтерін оқыту үрдісі

Жұмыстың гипотезасы -- 7-9 сыныптардағы геометриялық салу есептерін жүйелі түрде қарастыру, осы тақырып бойынша оқушылардың математикалық дайындық деңгейін көтеруге ықпал жасайды.

Дипломдық жұмыстың мақсаты және гипотезасы бірқатар мәселелерді шешу және тұжырымдауды қажет етеді.

Зерттеу мәселелері:

а) салу есептерінің мектеп геометриясы курсындағы орнын, атқаратын қызметін, мақсатын анықтау;

б) салу есептерінің 7-9 сыныптардағы мазмұнын анықтау;

в) салу есептерін шешудің кезеңдерін көрсету;

г) салу есептерін шешу тәсілдерін анықтау.

Көрсетілген мәселелерді шешу үшін келесі зерттеу әдістері қолданылады:

«Геометрия курсында салу есептерін шешу» тақырыбы бойынша ғылыми әдістемелік және оқу әдебиеттерін талдау;
мектеп оқулықтарын талдау және бақылау;
тәжірибелік жұмысты өткізу және оның нәтижелерін өңдеу.

Дипломдық жұмыс кіріспеден үш тараудан, қорытындыдан, педагогикалық тәжірибеден, пайдаланған әдебиеттер тізімінен тұрады.

Бірінші тарауда геометриялық салулар тарихы; конструктивтик геометрияның аксиомалары; құралдар аксиамалары; элементтар салулар берілген.

Екінші тарауда салу есептерін шешудің негізгі әдістері қарастырылған. Үшінші тарауда орта мектепте қолданылып жүрген геометрия оқулықтары бойынша салыстырмалы талдау жасалған.

I тарау. Геометрия курсындағы салу есептері

1. 1. Геометриялық салулар тарихынан

Геометрия - ежелгі математикалық ғылымдардың бірі. Алғашқы геометриялық деректерді вавилондық сына кестелер мен египеттік папирустарда ( б. э. д. III ғасырда) сонымен қатар, басқа дерек көздерден тапқан. «Геометрия» ғылым атауы ежелгі гректерде пайда болды. Ол «гео-жер «метрео»- өлшеймін деген екі грек сөзінен тұрады.

Қазір мектепте қолданылатын геометриялық терминдердің (атаулардың) көпшілігі сонау Ежелгі Грецияның өзінде - ақ қалыптасқан болатын. Грек терминдері жарым - жартылап сол көне заманның өзінде, кейініректе орта ғасырларда латын тіліне аударылғанды, ал латын тілі талай ғасырлар бойы ғалымдар тілі болып келген. Сондықтан геометрия терминдерінің көпшілігі грек немесе латын тілдерінен алынған. Мысалы: «Планиметрия» термині - орта ғасырлық термин, ол латынның planum - жазықтық деген сөзі мен гректің «метрео» - өлшеймін деген сөзінен шыққан. «Фигура» - латынның бейне, түр, кескін деген мағынадағы сөзі. Бұл термин XII ғасырдан бастап жалпылама қолданылатын болды. Бұған дейін онымен қатар сол ұғым үшін латынның басқа бір - «форма» деген сөзі қолданылды, бұл да, нәрсенін сыртқы түрін, сыртқы пішінін білдіретін сөз. «Сызық» - латынның linea деген сөзінен шыққан, ал мұның өзі linum - зығыр, зығыр талшығынан иірілген жіп, бау деген мағынадағы сөзден шыққан. Өлшеу жұмысында Рим жер өлшеуіштері осындай жіпті немесе бауды пайдаланған. «Циркуль» - латынның circulus - дөңгелек деген сөзінен шыққан.

Ең қарапайым салу есептері өте ерте заманда жер танаптарын өлшеу

және әр түрлі құрылыстарды салу жұмыстарын орындағанда пайда болған. Алғашқы мұндай есептер тобына мынадай есептер жатады: берілген кесіндіге тең кесінді салу, кесінділерді және бұрыштарды тең екі бөлікке бөлу, берілген нүкте арқылы берілген түзуге перпендикуляр жүргізу. Бұл есептердің шешуі гректерден бұрынғы дәуірдің өзінде - ақ белгілі болатын.

Біздің эрамызға дейінгі VII ғасырдан VIII ғасырға дейінгі уақыт аралығында грек ғалымдары геометрия саласында, жекелеп айтқанда салу есептері жөнінде аса көп материал жинап, оларды өңдеді. Бұл жерде бір жағдайды атап ескерту қажет: салу жұмысын орындағанда тек сызғыш пен циркуль пайдаланып, басқа аспаптар қолданылмағанда ғана мұндай салуды ежелгі грек ғалымдары геометриялық салу деп есептеген. Ал егер салу жұмысын орындағанда басқа аспаптар, мысалы сызбалық үшбұрыш, бөліктері бар сызғыш қолданылса, онда мұндай шешуді геометрилық шешу деп есептемеген.

Ерте заманнан бізге келіп жеткен деректерге қарағанда, б. э. дейінгі VI ғасырда өмір сүрген Пифагордың өзі дұрыс бесбұрышты және онбұрышты салу тәсілдерін және кейбір күрделірек салу есептерін тапқан. Салу есептерін шешу әдістерін жасау ісіне Платон (б. э. дейінгі V ғасыр) және оның шәкірттері үлкен үлес қосқан. Платон заманынан бері салу есептерін шешудің мынандай төрт кезеңі ажыратылып қарастырылатын болды: 1) анализ (талдау) ; 2) салуды орындау, 3) дәлелдеу және 4) зерттеу .

Кесіндіні қақ бөлудің біздің оқулықтарда көрсетілген тәсілі Прокл (410-485ж. ) комментариінде баяндалған, оның пікірінше, бұл тәсілді атақты грек математигі Аполлоний тапқан.

Евклидтің атақты «Бастамаларында» салу есептерін қарастыруға үлкен орын берілген. Евклид қандай да бір фигураның бар болатындығын дәлелдей отырып, ол фигураны тек сызғыш пен циркульді қолданып қалай салуға болатындығын көрсетіп отырған. Оның 13 кітабында көптеген салу есептері қарастырылған, олардың бірсыпырасы орта мектепте қазірде де қарастырылады.

Евклид «Бастамаларының» бірінші кітабында үшбұрыштарды салу тақырыбы енгізілген. Оның төртінші кітабында басқа мәселелермен бірге, дұрыс төртбұрышты, бесбұрышты, алтыбұрышты және онбесбұрышты салу мәселелері қарастырылған. Әсіресе бұрышты тең үш бөлікке бөлу (бұрыш трисекциясы) туралы есепке көп еңбек еткен. Алайда бұл есепті шешуге арналған барлық еңбек зая кетті. Бұл есепті тек сызғыш пен циркульді қолданып шешуге болмайтындығы қазіргі уақытта дәлелденді.

Геометриялық салу есептері - геометрияның міндетті тарауларының бірі болып саналады.

Геометриялық салулар - ол әртүрлі геометриялық құралдар көмегімен шешілетін кейбір геометриялық есептердің шешімі. Құралды таңдауға байланысты осы құралдармен шешілетін есеп циклі анықталады. Циркуль және сызғыш - адам қолданған алғашқы сызбалық құралдар. Циркуль және сызғыш геометриялық салулар үшін негізгі құралдар жиынтығы болып табылады. Егер ізделінетін нүкте координаттары берілген нүктелер координаттарына қолданатын қосу, көбейту, бөлу және квадрат түбірден арылу амалдарының шекті саны бар өрнектер түрінде жазылуы мүмкін болса, салу есебі циркуль және сызғыш көмегімен шешіледі. Егер мұндай өрнектер болмаса, онда есеп циркуль және сызғыш көмегімен шешілмейді.

Геометриялық фигураларды сызғыш және циркуль көмегімен салу шеберлігі жоғары дәрежеде Ежелгі Грецияда дамыған. Сол кезде орындай алатын, үш берілген шеңберді жанайтын шеңберді салу есебі салу есептерінің ең қиын есептерінің бірі болып табылады. Бұл есеп Пергидағы (б. э. д. 280-170ғ. ) әйгілі грек геометрі Апполоний атымен «Апполоний есебі» деп аталады.

Циркуль мен сызғышты пайдаланып салуға болмайтын есептерді шешуге геометриялық алгебра жарамсыз болды. Көп ұзамай осындай есептердің көп екендігі анықталды. Солардың ішінен математиканың ұзақ тарихи жолында сарапқа салынып, математиканың дамуына үлкен ықпал жасаған үш есепке тоқталайық.

а) Кубты екі еселеу есебі. «Көлемі берілген кубтың көлемінен екі есе үлкен куб салу керек». Бұл есеп ежелгі Грецияда кеңінен мәлім болғаны сонша, ол туралы ел аузында мынадай аңыз тараған: Делос аралында оба ауруы бұрқ ете қалады. Жұрт жиналып індетке құрбан шалады, соның ішінде куб пішіндес алтынды да «тасаттыққа» береді. Бірақ та індет тоқталмайды. Бұл пәледен құтылу жолын сұрағанда көріпкел - абыз «тасаттықтың» пішінін өзгертпестен екі есе үлкейтіңдер деп бұйырыпты. Содан бері бұл есеп «Делос есебі» деп аталып кетіпті.

Кубты екі еселеу есебінің шешуін (жалпы алғанда куб иррационалдықты) циркуль мен сызғыш арқылы салуға болмайтынын тұңғыш рет 1837 жылы математик Ванцель дәлелдеді.

ә) Бұрышты трисекциялау есебі. Берілген бұрышты тең үшке бөлу мәселесі -грек геометрлерін көп толғатқан мәселе. Біздің заманымызға дейінгі V ғ. Математигі Элидтік Гипий бұрышты үш бөлімге бөлу (трисекциялау) есебін шешу үшін айрықша бір қисық сызық -квадратрисаны -қолданады. Квадратриса -математика тарихында кездескен тұңғыш трансцендетті қисық. Мұндай қисықтарды қарастыру да болашақ математикада едәуір орын алды. Бұрышты тең үшке бөлудің басқа бір әдісін кейіннен Архимед ұсынды.

Бұрышты трисекциялау мәселесінің де тарихы өте ұзақ. Біздің заманымыздың IX-X ғасырларында Орта Азия математиктері ол есепті 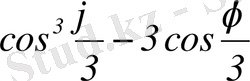немесе 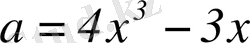куб теңдеуіне келтіреді. Ал мұндай куб теңдеулері циркуль мен сызғыш арқылы, яғни геометриялық алгебра әдістерімен шешуге болмайтыны тек XIX ғасырда дәлелденді.

б) Дөңгелекті квадраттау есебі (Берілген дөңгелекке тең аудандас квадрат салу) . Бұл есепті шешуді грек математиктері екі тұрғыда қарастырады. Біріншіден, олар мұны жуықтап шешуге көп әрекет жасаған. Мұнда дөңгелекті іштей және сырттай сызылған көп бөрыштар арқылы жуықтатып, шеңбер ұзындығының диаметрге қатынасын көрсететін санының жуық мәнін табу мақсаты көзделеді.

Екінші жағынан, математиктер дөңгелекті дәл квадраттауға тырысады. Бұл саладағы ізденістер ешбір нәтиже бермеді; өйткені, егер дөңгелек радиусын деп алсақ, есеп кесіндісін салуға тіреледі. Сөйтіп, бұл кесіндіні салу санының табиғатына тікелей байланысты болады. Бұл санның рационал бола алмайтыны XVIII ғасырдың аяғында ғана анықталды. Анығын айтқанда, бұл санның ешбір бүтін коэффициентті алгебралық теңдеудің түбірі бола алмайтынын, яғни транцендентті сан екенін 1882 жылы Линдеман дәлелдеді. Бұл дәлелдемесінде ол мұндай сандарды циркуль мен сызғыш арқылы салуға еш болмайтынын айтты. Сөйтіп, осы санның төңірегінде екі жарым мың жылға жуық жасалған әрекеттер бос әуре болып шықты. Алайда бұл ізденістер математика үшін босқа кеткен жоқ, ғалымдар оны шешу әрекеті үстінде көптеген математикалық жаңа фактілер тағайындады, соны әдістер ашты. Мәселен, қазіргі математикалық анализдегі шектер теориясының бастамасы болып табылатынын «сарқу әдісі» деп аталатын әдіс те осы дөңгелекті квадраттау есебіне байланысты табылған. «Сарқу әдісінің» бастамасы б. з. д. V ғасырда өмір сүрген философсофист Антифоннан басталады. Ол: «Дөңгелекке іштей квадрат салып, оның қабырғасын екі еселеп, одан шыққан көпбұрыштың қабырғасын тағы да екі еселеп, осы әрекетті біртіндеп жүргізе берсек, дөңгелекке іштей сызылған дұрыс төртбөрыштар тізбегі табылады. Бұлардың кейінгісі алдыңғысына қарағанда дөңгелекке жақын келеді де бір кезде онымен дәлме - дәл болады» деп пайымдаған. Бұл ұйғару бойынша дөңгелекті көпбұрыштар арқылы сарқуға болады, яғни көпбұрыш пен дөңгелек теңбе -тең болады. Антифон бұл ұйғаруын жоғарыдағы дөңгелекті квадраттау есебін шешуге қолданбақшы да болған.

Грек философтары әрі математиктері Антифонның бұл пайымдауын сынап ещбір көпбұрыштың дөңгелекке тең болмайтынын, бірақ дөңгелекті көпбұрыштар арқылы кез келген дәлдікпен жуықтауға болатынын дәлелдеп берді. Осы сияқты пайымдаулар мен қорытындылар негізінде дәл де қатаң әдіс -«сарқу әдісі» шықты.

Сонымен циркуль және сызғыш көмегімен орындалатын салу есептері XIX ғасырдың соңында дамыған және бүгінде математиканың ең қызықты бөлімі, сонымен қатар жүз жыл бойы мектептегі геометрия курсының дәстүрлі материалы болып есептеледі.

1. 2. Конструктивтік геометрияның ортақ аксиомалары

Геометриялық салуларды зерттейтін геометрияның тарауын конструктивтік геометрия деп атайды. Конструктивтік геометрияның негізгі ұғымы - фигураны салу болып табылады. Бұл ұғым анықтамасыз қабылданады. Оның нақты мағынасы практикадан белгілі, мұнда «жүргізу» (түзуді), «белгілеу» (нүктені) және т. б. Осы ұғымды сипаттайтын негізгі талаптарды (постулаттар) дұрыс баяндалып және анық тұжырымдалуы қажет. Бұл талаптар, әдетте, мектеп курсындағы элементар геометрия шарттарында тұжырымдалмайды, бірақ кез келген салу есептерін шешу процесінде өз-өзінен түсінікті мәселе ретінде жобаланып түсініледі. Конструктивтік геометрияның негізгі талабы сызба практикасының ең маңызды кезеңдерін абстрактілі түрде өрнектейді. Олар аксиомалар болып табылады, дәлелдеусіз қабылдап, келешекте конструктивтік геометрияның логикалық негізі болып қызмет атқарады. Осы геометриялық салулар теориясының негізгі аксиомаларын қарастырамыз.

Егер қандай да бір фигура берілді десе, онда бұл кезде ол бейнеленген, сызылған, яғни салынған екені жобалап түсініледі. Сонымен, конструктивтік геометрияның бірінші негізгі талабы мынада:

1. Бір берілген фигура салынған.

Айталық, және жарты шеңбері салынған (1-сурет) . Әрине, бұдан кейін толық шеңбер салынды деп есептеу керек.

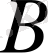
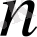
1-сурет

Дәл осылай, егер кейбір түзудің сәулесі салынса, одан кейін сол түзудің сәулесі салынса, онда осы сәулелерді қосатын түзуі салынды деп есептелінеді.

2-сурет

2. Егер екі ( немесе одан да көп) фигуралар салынған болса, онда бұл фигуралардың қосылуы да салынады.

Айталық, бір түзудің екі кесіндісі салынған. Кесіндіні толығымен екінші кесіндіде жатады ма (3-сурет) немесе жатпайды ма (4-сурет) деген сұраққа жауап беруге мүмкіндік береді.

3-сурет

4-сурет

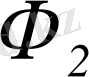Егер шеңбер және нүкте салынған болса, онда сызбаны тікелей қарастыру арқылы нүкте шеңберге тиісті ме, әлде тиісті емес пе деген сұраққа жауап беруге болады. Жалпы, егер екі фигура салынған болса, онда біреуі екіншісінің бір бөлігі болып табылады ма, әлде табылмайды ма екені белгілі. фигурасы фигурасының бір бөлігі болып табылады, сонда тек сонда, егер айырмасы бос жиын болса, онда үшінші талапты (постулатты) келесі түрде беруге болады.

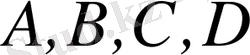
3. Егер екі фигура салынған болса, онда олардың айырмасы бос жиын болатынын не болмайтынын анықтауға болады. -түзудің төрт нүктесі болсын (сурет 5) .

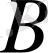
5-сурет

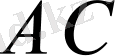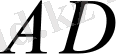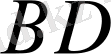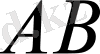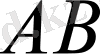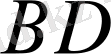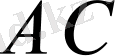Айталық, және кесінділері салынды. Онда бізде және кесінділерінің айырмасы болып табылады. кесіндісі салынды деп есептейміз, сол сияқты кесіндісі және кесінділерінің айырмасы болып табылады.

4. Егер екі салынған фигуралардың айырмасы бос жиын болып табылмаса, онда бұл айырма салынған.

Екі түзу сызып, біз олардың қиылысатынын не қиылыспайтынын айта аламыз. Сол сияқты, егер екі шеңбер салынған болса, онда сызбадан олардың ортақ нүктелерінің бар жоқтығын айта аламыз. Бұл кез келген екі фигураға қатысты. Сонымен:

5. Егер екі фигура салынған болса, онда олардың қиылысуы бос жиын болатынын не болмайтынын анықтауға болады.

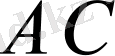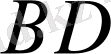Егер шеңбер және нүкте салынған болса, онда нүкте шеңберге тиісті немесе тиісті емес екені белгілі болу керек. Егер екі шеңбер салынған болса, онда олардың ортақ нүктелері бар немесе жоқ екенін айтуға болады. Қайтадан сурет 5-ті қарастырайық. және кесінділері салынғаны белгілі болсын. Бұл жағдайда екі кесінділердің қиылысуы болып табылатын 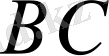кесіндісі де салынған деп есептейміз. Егер екі қиылысатын шеңберлер сызылған болса, онда біз олардың екі қиылысу нүктесі салынған деп есептейміз. Мұндай текті келісімділіктер келесі түрде беріледі:

6. Егер екі салынған фигуралардың қиылысуы бос болмаса, онда ол салынған.

Келесі негізгі екі талапта жеке нүктелерді салу мүмкіндіктері жайында айтылған.

7. Салынған фигураға тиісті екенін біле тұра нүкте салуға болады.

8. Салынған фигураға тиісті емес екенін біле тұра нүкте салуға болады.

7- аксиома салынған фигураға тиісті нүктені салу мүмкіндігін анықтайды. 8- аксиома кейбір жаңа нүктелерді салуға мүмкіндік береді, бірақ бұл нүктелерге ешқандай жаңа қасиеттер жазылмайды. 1-8 дейінгі талаптар- конструктивті геометрияның жалпы аксиомалары.

1. 3 Құралдар аксиомасы

Геометриялық салуларда көп қолданылатын құралдар сызғыш (біржақты), циркуль, екі жақты сызғыш болып табылады. Геометриялық салулар құралын тек сызғыш және циркульмен шектеу ежелден шыққан. Евклидтің (б. э. д. III-ғасыр) әйгілі геометриясы циркуль және сызғышпен орындалатын геометриялық салуларға негізделген; сонымен бірге циркуль және сызғыш тең құқықты құралдар ретінде қарастырылады. Сызғышқа қарағанда, циркуль жетілген, тура құрал болып табылады, кейбір салуларды сызғыштың көмегінсіз, тек циркуль мен орындауға болатыны ертеден ескерілген, мысалы, шеңберді тең алты бөлікке бөлу; берілген түзуге қатысты берілген нүктеге симметриялы нүкте салу және т. б. аксиомаларды тұжырымдауға көшейік.

А. Сызғыш аксиомасы.

Сызғыш келесі геометриялық салуларды орындауға мүмкіндік береді:

а) берілген екі нүктені қосатын кесінді алу;

ә) берілген екі нүкте арқылы өтетін түзу салу;

б) берілген нүктеден шығатын, берілген екінші нүкте арқылы өтетін сәуле салу.

Ә) Циркуль аксиомасы.

Циркуль келесі геометриялық салуларды орындауға мүмкіндік береді:

а) егер центрі және шеңбер радиусына тең кесінді салынған болса, шеңбер салу;

ә) егер щеңбер центрі және доға ұштары салынған болса, онда доға салу.

Б. Екі жақты сызғыш аксиомасы.

Екі жақты сызғыш келесі салуларды орындауға мүмкіндік береді:

а) А аксиомада айтылған кез келген салуды орындайды;