Қарапайым логарифмдік теңдеулер

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 49 бет
Таңдаулыға:

Аннотация

Мектеп математика курсында жалпы логарифм тақырыбы жоғары
сыныптарда алгебра және анализ бастамаларында оқытылады. Ең алдымен
логарифмнің анықтамасы, қасиеттері, графигі түсіндіріледі, содан кейін
логарифмнің функциясына тоқталады. Логарифмдік теңдеулер мен теңсіздіктерді
оқушыларға түсіндіруде олардан өздерінің алгебрадан алған білімдері талап
етіледі. Яғни, логарифмдік теңісіздіктерді шығарғанда интервалдар әдісі,
теңдеулер жүйесіне келтіу шарттары пайдаланылады.
Дипломдық жұмыстың құрылымы: Кіріспе, 1 тарау, 2 тарау, қорытынды
және пайдаланған әдебиеттер тізімі.

МАЗМҰНЫ

Кіріспе
1 Логарифмдік
функциялар ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... .5
1.1 Тарихи
мағлұматтар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... 5
1.2 Логарифмдер және олардың
қасиеттері ... ... ... ... ... ... . ... ... ... ... ... .. 14
1.3 Логарифмдік функциялар және олардың
қасиеттері ... ... ... ... ... ... . ..18
2 Логарифмдік теңдеулер мен теңсіздіктерді
шешу ... ... ... ... ... ... ... ... ... ... . 25
2.1 Қарапайым логарифмдік
теңдеулер ... ... ... ... ... ... .. ... ... ... ... ... ... ... . 25
2.2 Күрделi логарифмдік
теңдеулер ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... . . 31
2.3 Түрлі логарифмдік
теңдеулер ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ...
39
2.4 Логарифмдік
теңсіздіктер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... 48

Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... 59
Пайдаланған
әдебиеттер ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ... ...60

Кіріспе

Жаңа әлемдегі жаңа Қазақстан құру біздің жеке адамдардың,
қоғамның және еңбек рыногының талаптарын қанағаттандыра алатын
бәсекеге қабілетті білім беру жүйесін қалыптастыруды талап етіп
отыр. Осы орайда Білім туралы жаңа заңда дәл осы бәсекеге
қабілетті отандық білім беру жүйесін қалыптастыру туралы айтылған.
Қазіргі жалпы нарықтық экономикалық ғылым математиканы кеңінен
қолданумен сипатталып, математикалылық әдістер барлық экономикалық
ілімдердің, оның ішінде экономикалық теорияның ең негізгі бөлімі
болып есептеліне бастады. Жан – жақты терең жасалған экономикалық
ғылымда және өндірістік тәжірибеде жаңа мүмкіндіктер ашты.
Математикалық экономикада және басқа ғылымдарда кеңінен
қолданылуы осы ілімнің өзіне тән ерекшелігі болып табылады.
Егер оның осы ерекшелігі түбегейлі экономикалық талдаумен
біріктіре отырып пайдаланылса, онда өндірістік жұмыстарды тиімді
ұйымдастыруда және басқаруда яғни әр істе ұтымды табыс табу
жолдарында математиканың маңызы зор.
Тақырыптың көкейкестілігі. Мектеп математика курсында логарифмдік
теңдеу мен теңсіздіктердің қарапайым, дербес жағдайлары ғана қарастырылады.
Логарифмдік теңдеулер мен теңсіздіктерді қандай жолмен шығарсақ та есептің
дұрыс шешілуі олардың қасиеттерін дұрыс қолдана білуге байланысты.
Жұмыста түрлі логарифмдік теңдеулерді олардың қасиеттерінен пайдаланып
шығарудың, логарифмдік функциялардың графигін салудың, анықталу облысын
табудың жолдары қарастырылған. Кейбір жағдайда теңдеулерді шығарудың жылдам
шешу тәсілінде логарифмнің 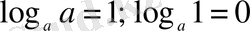түріндегі формасы қолданылады.
Логарифмдік теңдеулер мен теңсіздіктерді шешудің тәсілдері әртүрлі
болады. Әдетте есеп шешу әдісінің біреуі арнайы алынғаны есепте
көрсетіледі, есептің мазмұны оны шешу тәсілінің негізі болады. Бірақ, осы
жағдайда бұл тәсіл оқушының санасында есеппен байланысты, ал оның өзіндік
мәні анықталмайды. Ал егер әртүрлі тәсілдерді бір ғана есепке қолданып
көрсе онда олардың қайсысы тиімді екені анықталады. Әр әдістің ерекшелігі,
артықшылығы және кемшіліктері есептің мазмұнына қарай айқындалады.
Дипломдық жұмыстың мақсаты: Логарифмдік теңдеулер мен теңсіздіктерді
шешудің негізгі тәсілдерін игеру барысында, есеп шығарудың теориялық,
әдістемелік және практикалық негіздемелерін жасау.
Зерттеу пәні: Математиканы оқыту
Зерттеу нысаны. Логарифмдік теңдеулер мен теңсіздіктерді шешу
тәсілдері.
Дипломдық жұмыстың әдіснамалық негізі:
- зерттелетін тақырып бойынша математикалы ғылыми-әдістемелік,
психологиялық-педагогикалық,философ иялық әдебиеттерге талдау жүргізу;
- орта білім мен математикалық деңгейі туралы нормативтік құжаттарды
талдау;
- математика мұғалімдерінің алдыңғы қатарлы тәжірибесін оқу және
жалпылау.
Зерттеу жұмысының міндеті:
- мектеп курсында оқушыларға логарифмдік теңдеулер мен теңсіздіктер
тақырыбын терең ұғындырудың қажеттілігін ашып көрсету;
- логарифмдік функцияның қасиеттері мен графигін саналы түрде
оқушыларға түсіндіру.
Зерттеудің ғылыми жаңалығы:

Жұмыстың практикалық маңыздылығы:

1 Логарифмдік функциялар

1.1 Тарихи мағлұматтар

Логарифмдердің пайда болуы XVI ғасыр бойында астрономия және басқа
ғылыми-практикалық әрекеттер барысында жуық есептеулердің саны көбейіп,
маңызы арта түседі. Өлшеу, бақылау құралдары жетілдірілген сайын
астрономияға аса қажетті тригонометриялық кестелердің дәлдігі мен маңызы
артады. Әлемнің жаңа жүйесінің жасау жолындағы планеталар қозғалысын
зерттеу бұрын болып көрмеген есептеу жұмысына негізделді.Мысалы, Марс
планетасының орбитасын анықтау үшін Кеплер көп жылдарын математикалық
есептеуге жіберген. Мұндай қиындықтар практиканың басқа салаларында да орын
алады. Мәселен, финанс және қамсыздандыру ісінде күрделі проценттер
кестесін жасау т.б. Басты қиыншылық көп таңбалы сандарды, әсіресе
тригонометриялық шамаларды көбейту және бөлу амалдарын орындауда болды.
Көбейтуді одан жеңілірек қосу мен азайтуға келтіру үшін кейде
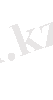sinxsiny= ,
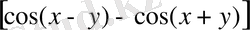cosxcosy=
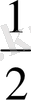
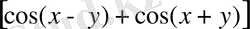
ережелері бойынша синус және косинус кестелері пайдаланылды.
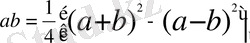ережесі бойынша екі санды көбейтуді жеңілдетеу үшін 100000-ға дейінгі
сандардың квадратының кестесі жасалынады. Алайда бұл әдістер есептеу
проблемасын қанағаттанарлық түрде шеше алмады. Оны түбегейлі шешу
логарифмдер кестесін жасауды талап етті. Логарифмдердің ашылуы XVI ғасырдың
соңында анықталған прогрессиялар қасиеттеріне негізделді. Жоғарыда атап
өткендей математик Штифель

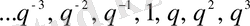
және ... 3, -2, -1, 0, 1, 2, 3, ... прогрессияларын салыстыра келіп,
геометриялық прогрессиядағы көбейту, бөлу, дәрежелеу, түбір табу амалдарына
арифметикалық прогрессиядағы қосу, азайту, көбейту және бөлу сәйкес
келетінін көрсетті. Бұл логарифм идеясының түп қазығы еді, өйткені санның
логарифмі сол санды табудағы негізді дәрежелеуге қажетті көрсеткіш
болып табылады. Тек жалпы мүшесі 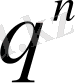болатын прогресс қасиеттерін кез
келген нақты көрсеткіш жағдайына ауыстыру керек болды. Осыдан кез келген
нақты мәнді қабылдайтын көрсеткіштік функциясы мен оған кері логарифмдік
функциясының қасиеттерін білу туындайды. Бұл терең принциптік идея бірнеше
он жылдан кейін барып, XVII ғасырдың басында дамытылып, қазіргі
логарифмдердің пайда болуына себепші болды.
Мұндай идеяларды амалдарды оңайлатуға қолдану үшін дәреже көрсеткіштер
тізбегіне дәреженің мәндер тізбегі сәйкес келетіндей кестелер жасау
қажеттілігі туады. Кестенің ортақ негізін бірге жуық келетіндей етіп таңдап
алу керек болды. XVII ғасырда мұндай кестелер құрастырыла бастайды. Мұндай
кестелердің бір нұсқасын Стевин жасаған.
Бұл күрделі проценттер кестелері яғни проценттік ұтысының 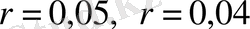т.б.
мәндеріне қарай 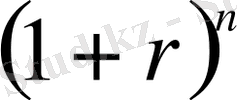сандары мәндерінің кестелері еді. Мұнда r-дің мәні аз
болған сайын алынған мәндер арасындағы алшақтық кеми береді. осыған ұқсас
кестені ең алғашқы логарифмдік кестелердің біріне негіз болған И. Бюрги
құрастырған кесте еді.
И. Бюрги (1552-1612) Швейцарияда туып өсті. Ол сағат және астрономиялық
аспап-құралдарды жөндеу шебері болған. Прагада біраз қызмет атқарып, И.
Кеплердің астрономиялық бақылаулары мен қыруар есептеулеріне көмектескен.
Есептеу жұмыстарды жеңілдету мақсатында ол сегіз жыл (1603-1611) бойы
ерінбей еңбек етіп, 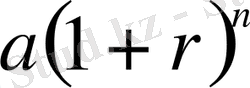түріндегі Стевин кестелері негізінде өзінің
логарифмдік кестесін жасаған.
Кестенің адымы жетерліктей аз болуы үшін Бюрги 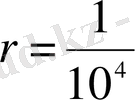мәнін алады.
Бөлшек мәндерден барынша құтылу мақсатында ол қосымша 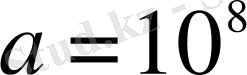көбейткішін
енгізеді. Сонда шыққан 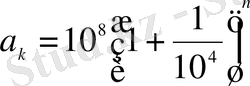гометриялық прогрессиялардың мәндеріне (k – 0,
1, 2, 3, ...) Бюрги 0, 10, 20, 30, ... арифметикалық прогрессиялар мәндерін
сәйкес қояды. Сонда мәндердің екі тізбегі келіп шығады:

0 10, 20, 30, ... .
Төменгі қатардағы сандар қызыл бояумен басылып, қызыл сандар, ал
жоғарғы қатардағы сандар қара бояумен басылып, қара сандар деп аталған.
Сонымен Бюрги кестесіндегі қызыл сандар негізі 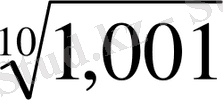болғандағы -
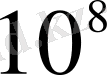ге бөлінген қара сандардың логарифмі болып табылады. Бюргидің кестесі қызыл
сандарды табуға бағытталғандықтан, ол шын мәнінде антилогарифмдер кестесі
болып шығады. Мұның, әрине, принциптік айырмашылығы жоқ. Қара сандарды
есептеу тоғыз таңбаға дейін жүргізіледі. Ол 109-ға тең толық қара санға
жеткізіледі. Осыған сәйкес қызыл сандар интерполяцияның көмегімен
есептеледі, ол 230 270 022, яғни 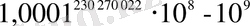болады. Міне, осыдан-ақ Бюргидің
қаншама орасан зор аралық есептеулерді жүргізуге мәжбүр болғаны байқалады.
Бюрги есептеу жұмысындағы кестелердің пайдасын көре тұра көпке дейін
оларды жарияламайды. Тек 1620 жылы ғана барып Кеплердің талабы бойынша
Арифметикалық және геометриялық прогрессиялар кестелері және әр түрлі
есептеулерде оларды қалай пайдалану жөніндегі тыңғылықты (байсалды)
нұсқаулар кітабын бастырып шығарады. Бұл кестелердің түпнұсқасы Кеплер
архивының басқа да материалдарымен бірге СССР-да Пулков обсерваториясында
сақтаулы тұр.
Бюргидің кесте жасаудағы жайбарақаттығы қымбатқа түседі. 1614 жылы одан
6 жыл бұрын Англияда Логарифмдердің ғажайып кестелеріне сипаттама атты
еңбек жарық көреді. Мұның авторы шотландиялық барон Джон Непер (1550-1617)
математика тарихында логарифмдерді бірінші ашушы атағына ие болады.

Непердің логарифмі. Ондық логарифмдер Непер кестелері 00-ден 900-қа
дейінгі бір минуттік адыммен есептелген 8 таңбалы тригонометриялық
функциялар кестелері еді. Непердің принципиалды жаңалығы прогрессиялардың
дискретті мәндерін салыстырудан бас тартып, үздіксіз екі шкаладан тұратын
логарифмдік функционалдық тәуелділіктерді қарастыру болды. Оның идеясы
мынадай еді:
А және А1 нүктелерінен бір кезде стрелкамен көрсетілген бір бағытта M
және m нүктелері қозғалсын делік. Олар біртіндеп М0, М1, М2, М3, ... және m0,
m1, m2, m3 нүктелерінен өтетін болсын. Екі нүктенің бастапқы жылдамдықтары
бірдей (айталық, 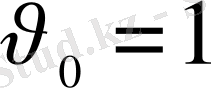). m нүктесі 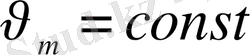, тұрақты, ал М нүктесі
баяулатылған жылдамдықпен қозғалсын. М нүктесінің жылдамдығы В нүктесіне
дейінгі қалған ара қашықтыққа пропорционал болсын (оңай болу үшін AB=1 деп
аламыз). 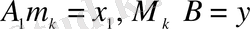деп белгілесек, қазіргі математика тілінде 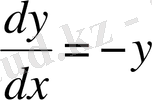теңдеуіне
эквивалент болады. Мұнан 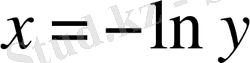немесе 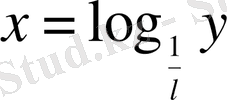. Сөйтіп, Непердің логарифмдік
жүйесі негізі болатын жүйе болып шығады. Алайда Непер 1614 жылы
логарифмдік функция идеясын әлі айқын да толық меңгере қоймаған еді. Оның
мақсаты тек кестелер жасау болды. Сондықтан ол AB-ны 107 уақыт моменті
ішінде жүріп өтетіндей 107 аралыққа бөледі. Сонда бірінші моменттегі
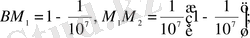
жылдамдық x=1, сонан кейін біртіндеп: 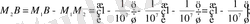, ..., т. с. с.
Осылай мәндердің екі тізбегі түзіледі:

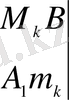
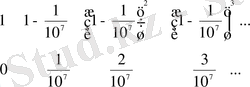
Непер бөлшектерден құтылу үшін AB=1 орнына AB=107 деп алады.
Кестедегі төменгі сандарды ол жоғарыдағы сандардың сәйкес логарифмдері
деп атайды. Логарифм деген термин гректің екі сөзінен логос - қатынас,
аритмос - сан, яғни қатынастар саны дегенді білдіреді. Бұл терминді
ғылымға енгізген Непердің өзі. Осылай атау арқылы ол логарифмдердің сәйкес
сандар қатынастарын өлшеуге арналған қосымша сандар болатынын айқын
ажыратып береді. Непер логарифмдері үздіксіз сан шкаласы идеясына
негізделгенмен, сайып келгенде, екі прогрессияның: арифметикалық және
геометриялық прогрессияларды салыстыру кестелері болып шығады.
Непер жүйесі бойынша логарифмдеу ережелерінің қазіргіден өзгешелігі
бар. Олар ауыр және шұбалаңқы, өйткені 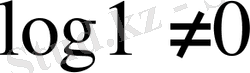(қабылдау бойынша ).
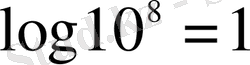Мысалы y=ab көбейтіндісінің логарифмдеу үшін оны 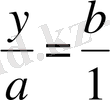түрінде жазып алады.
Қатынастар теңдігінен қатынастар сандарының (логарифмдерінің)
айырмаларының теңдігі туындайды:

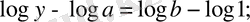
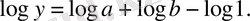
Непер кестелері таза тригонометриялық есептеулерге арналғандықтан,
берілген кез келген сандарға амалдар қолдануға қолайсыз болды. Мұндай және
басқа ыңғайсыздықтардан құтылу үшін 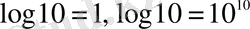деп алып, логарифмдер кестелерін
жасауды ұсынады. Бұл идеяны ол 1615 ж. осы мәселе төңірегінде зерттеулермен
айналысып жүрген Лондон колледжінің профессоры Генри Бригспен (1561-1630)
бірігіп жасауды жөн көрді. Бригс Шотландияға Неперді екі рет іздеп келіп,
онымен достасады, қызметтес болады. Осының нәтижесінде,
... 0,01 0,1 1 10 100
... -2 -1 0 1 2
прогрессияларын салыстыруға негізделген жаңа, практикалық жағынан өте
қолайлы ондық жүйе жасалады. Осыдан кейін Бригс өз бетімен ондық
логарифмдер кестесін жасауды қолға алады. 1617 ж. 1-ден 103-ке дейінгі
сандардың 8 таңбалы кестелерін жарыққа шығарады. Жеті жыл өткеннен соң,
яғни 1624 ж. 1-200 000 және 90 000-100 000 сандарының 14-таңбалы
логарифмдері келтірілген Логарифмдік арифметиканы жариялайды. Жаңа
есептер құралын насихаттау мақсатында ол кестелерді есептеу әдістерін және
логарифмдерді қолдануды түсіндіруге арналған бірнеше мақалалар шығарады.
Непер және Бригс еңбектері арқасында есептеу қиындықтарынан арылып,
математикада бұл бағытта жаңа мүмкіндіктер ашылады. Бұл әдіс логарифмдік
есептеу практикасында кең қолдау тауып, барлық елдерге тез таралады.
Логарифмдердің ашылуының практикалық пайдасымен қатар терең теориялық
маңызы болды. Ол логарифмдік, көрсеткіштік функциялардың табиғатын,
қасиеттерін түсінуге жол ашты. Кестелер жасау процесінде есептеу
практикасында айнымалы шамалар талдауларының элементтері пайда болады[1].
Астрономияда кездесетін көп мәселелер сан жүзінде есептеуді талап етті.
Бұл есептеулердің біразы дәреже және дәреже көрсеткіш ұғымдарының
дамуымен байланысты болды .
Арифметикалық амалдар тек бүтін сандар мен бөлшектерге ғана қолданылып
келді. Ондық бөлшектердің өзін европалықтар 1585 жылдан бастап қолдана
бастады. Оларды Европада тұңғыш енгізген – Бельгия инженері С.Стевин (1548-
1620 ).
Ол кезде тригонометриялық таблицалардың ролі тіпті орасан үлкен болды.
Сондықтан XVI ғасырдың аяғында, XVII ғасырдың бас кезінде бірнеше
таблицалар жасалды. Бұл таблицаларға ат салысқандар – Коперник, Кеплер және
олардың шәкірттері мен қызметкерлері. Бұл таблицалар кімге керек?
Біріншіден, олар астрономдарға, мұхиттар мен теңіздерде жүзушілерге,
құрылыс қызметкерлеріне тағы басқаларға керек. Ондық бөлшектер көп уақытқа
дейін Европада қолданылмаған себепті бұл таблицалардың қолайсыз жақтары
да болды. Аса мұқияттылықты талап еткен мәселе кішкене доғалардың
синустарын үлкен дәлдікпен есептеу болды.
Ол үшін ертедегі математиктерден мирас болып қалған әдіс – шеңберге
іштей сызылған дұрыс көпбұрыштардың қабырғаларын біртіндеп екі еселеу әдісі
– пайдаланылды. Мәселен, Виет 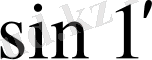табу үшін шеңберге іштей сызылған
дұрыс көпбұрыштардың қабырғаларының санын 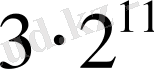-ге, ал сырттай сызылған
көпбұрыштардың қабырғаларының санын -ге жеткізді. Осының барлығы
- дің жуық мәнін үлкен дәлдікпен табуды талап етті.
Есептеуді жеңілдететін құралдар – ол кезде де, қазірде де таблицалар.
Практикалық есептеулерде көп кездесетін мәселелердің бірі - әр түрлі
сандарды негіздері бірдей дәрежелер түрінде көрсете білу болды. Бұл
проблема математикаға логарифм ұғымын енгізуге себепші болды. Европа
жеріне логарифмдер XVII ғасырдың басында енді. Олардың теориялық негіздері
тіпті ерте заманнан бастап қалыптаса бастады. Бұл теориялық негіздердің
идеясы екі прогрессияны, атап айтқанда, геометриялық прогрессия мен
арифметикалық прогрессияны салыстыруда және дәреже ұғымын жалпылауда болды.
Мына 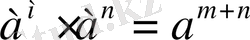ережесін Архимедтің және Диофанттың еңбектерінде кездестірген
болатынбыз.
Логарифм операциясына дайындық жасағандар – Штифель және Стевин. Мұнда
Штифель геометриялық прогрессияның мүшелеріне қолданылатын амалдармен,
онымен салыстырылатын арифметикалық прогрессияның мүшелеріне қолданылатын
амалдардың арасындағы байланысқа көңіл аударады. Атап айтқанда былай:
геометриялық прогрессияның мүшелеріне қолданылатын көбейту, бөлу, дәрежелеу
және түбір табу амалдарына арифметикалық прогрессияда қосу, азайту, көбейту
және бөлу амалдары сәйкес келеді.
Штифельдің келтірген таблицалары келесі екі прогрессия:
0 , а ,2а ,3а ,4а , ...

Үлкен сандар кездесетін есептеуді жеңілдету үшін, геометриялық
прогрессия мүшелерінің арасындағы аралықты толтыру және мүмкін болғанша әрі
қарай созу керек болды. Ол үшін геометриялық ортаны, ал арифметикалық
прогрессияда арифметикалық ортаны қою керек болды. Мұндай операцияны іс
жүзінде асыру үшін геометриялық прогрессияның тетелес екі мүшесінің
көбейтіндісінен квадрат түбір табу керек те, ал арифметикалық прогрессияда
қатар тұрған екі мүшенің қосындысын қақ бөлу керек. Мәселен, төмендегідей:
0 , 1, 2, 3, 4, ... ,
1, 2, 4, 8, 16, ... ,
Штифель таблицасындағы екінші және үшінші мүшелердің арасындағы
аралықты толтыру үшін, 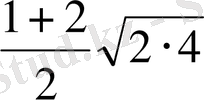сандарын есептеп шығаруға тура келеді. Міне,
осындай операцияны бірнеше рет қолданып, келесі мүшелердің арасындағы
аралықты толтыруға болады. Толтырылатын аралықты кішірейтіп есептеуді
азайтуға болады.
Штифельдің осы идеясын, яғни оның таблицасын, практикалық есептеуге
пайдаланған адам швейцариялық сағатшы, жөнді білім алмағанмен дарынды
математик болған Иобсту Бюрги (1552-1632) еді. Ол 1620 жылы Прагада басылып
шыққан.
Прогрессиялардың арифметикалық және геометриялық таблицалары атты
еңбегінде Штифельдің осы идеясын есептеу мәселелеріне қалай пайдалануға
болатынын баяндаған.
Геометриялық прогрессияның мүшелері бір – біріне жуық болу үшін, Бюрги
оның еселігін 2 емес 1 – ге жуық етіп, атап айтқанда, 1,0001 етіп алды.
Сонда геометриялық прогрессияның мүшелері баяу өседі және олардың қатар
тұрған мүшелерінің бір – бірінен айырмашылығы да аса үлкен болмайды.
(1) прогрессиялардағы а – ның орнына 0,0001 – ді алса, онда төмендегі
екі прогрессия шығады:
0 ; 0,0001 ; 0,0002 ; 0,0003 , ...
(2)
1 , 1,0001 ; ( 1,0001) , ... .
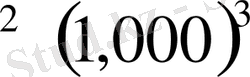(3)
Арифметикалық прогрессияның мәні 1-ге тең мүшесіне геометриялық
прогрессияның қандай мүшесі сәйкес келсе, сол мүшенің мәні таблицалардың
негізіне алынған. Мәселен, Штифель таблицаларының негізі 2-ге тең.
Кейінгі Бюрги таблицаларының (3) негізгі геометриялық прогрессияның
10001 – ші мүшесі, яғни 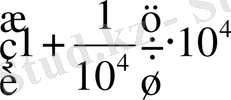саны болады, өйткені арифметикалық
прогрессиядағы оған сәйкес келетін мүше
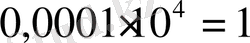
Бюрги мына 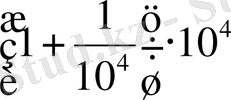санның жуық мәнін сегіз ондық таңбаға дейінгі
дәлдікпен тапты. Ол мынау:
2,71814593
Егер 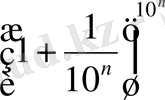өрнегіндегі - ді шексіз өсе береді десек, онда бұл өрнектің
шегі белгілі е саны болатыны математикалық анализден белгілі.
Европа жеріне жаңа ғана енген ондық бөлшектер алгоритмі XVII ғасырдың
бастапқы жылдарына дейін бір ізге келе қоймайды. Сондықтанда таблицалар
жасағанда кездесетін бөлшектермен әуре болмау үшін, Бюрги қосымша
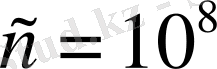көбейткішті енгізіп, 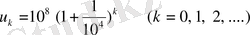геометриялық прогрессияға сәйкес мынадай
арифметикалық прогрессияны алды:
0; 10; 20; 30; ... ; 500; ...
Сөйтіп, төмендегі екі қатар сандар шығатын болды:
0; 10; 20; 30; ... ;

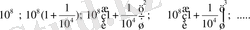
Жоғарғы қатардағы сандар қызыл бояумен басылды да, оларды қызыл
сандар деп атады, ал төменгі қатардағы сандар қара бояумен басылды да
оларды қара сандар деп атады.
Сонымен, Бюрги таблицасындағы қызыл сандар 10 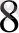- ге бөлінген
қара сандардың негізі 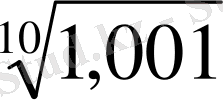-не тең логарифмдері болып табылатын болды.
Қара сандарды есептеуді Бюрги тоғыз таңбаға, яғни 10 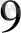санға, тең
толық қара санға дейін жеткізді. Оған сәйкес толық қызыл сан
230 270 022, яғни 1,0001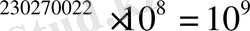, болды.
Осындай таблицаны құруға Бюрги сегіз жыл уақыт жұмсаған: сандардың
логарифмдерін есептеп шығару үшін 1,0001 санына 230 миллион рет көбейту
жүргізген.
Бюрги бұл таблицаларын жарыққа шығаруға көп уақытқа дейін батылы
жетпей жүрді. Бірақ Кеплердің бірнеше рет ескертуімен ол 1620 жылы
таблицаларын жарыққа шығарды. Оның осы еңбегінің тұп нұсқасы Совет еліндегі
Пулков обсерваториясында сақтаулы.
Бюрги таблицалары есептеу істерінің дамуында тиісті роль атқарды,
бірақ антилогарифмдер таблицалары болғандықтан, олармен пайдалану қиынырақ
болды.
2. 1614 жылы Бюргидің кітабынан алты жыл бұрын Англияда Логарифмдердің
таң – тамаша таблицаларын баяндау атты еңбек жарыққа шықты. Бұл еңбектің
авторы шотландиялық Джон Непер (1550-1617) еді.
Джон Непердің қарастырған мәселесі заманына сай келді. Бұл кезде
мұхитта жүзу үстемдігі Англияда болатын. Ағылшын теңізшілері өте күрделі
есептеулерді керек ететін астрономиялық таблицалардың болуын талап етті.
Бұл тілекті Непердің зерттеулері азды – көпті қанағаттандырды.
Бюрги өз таблицаларын жасағанда геометриялық прогрессияның еселігін
бірге жуық етіп алып, оның мүшелерінің арасын жиелетті. Қанша жиілеткенмен,
прогрессияға енбей қалатын, сондықтан логарифмдері бірден табыла қоймайтын
сандар қашан да болады.
Непер өзінің алдына қойған проблемасына тереңнен қарады. Оның заманында
үздіксіз процестерді, шамаларды зерттеу әдістерін математиктер игермегенді.
Алайда логарифмдердің үздіксіз шкаласын құру идеясын Непер дұрыс көрсете
білді. Міне осының арқасында әрбір оң санның логарифмі есептеліп табылатын
болды.
Непердің идеясы былай: А және В екі нүкте Ох және Оу түзулерінің
бойымен О және 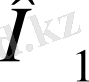нүктелерінен бір мезгілде шығып, қозғалатын болсын.
Айталық А нүктесінің жылдамдығы тұрақты да, ал В нүктесінің жылдамдығы мен
А нүктесінің жылдамдығының қатынасы, 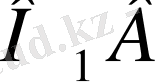мен бүкіл 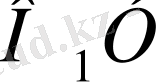кесіндісінің
қатынасындай болсын, яғни егер ОА=х, 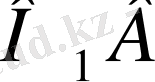=у, 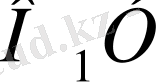=а болса, онда
математикалық анализ тілімен айтқанда х пен у–тің арасындағы тәуелділік
былай болар еді:

Бұл шыққан дифференциалдық теңдеу. Оны интегралдап, мынаны табамыз:

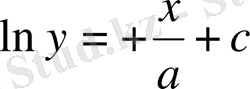
Енді мұндағы С – ні табу керек. Ол үшін x=0 болғанда у=а болады деп
ұйғарамыз, сонда

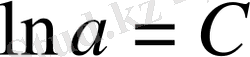
Ендеше

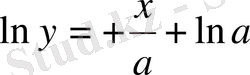
Бұдан

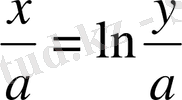
Жоғарыдағы дифференциалдық теңдеу Непердің ойында ешбір болған емес.
Соған қарамастан х пен у – тің арасындағы байланысты Непер тауып х
сандарын у сандарының логарифмдері деп атады. Логарифм деген сөз гректің
екі сөзінен тұрады: логос - қатынас, аритмос - сан.
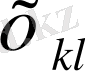сандары мен олардың логарифмдерінің арасындағы байланысты Непер
мына түрде тапты:

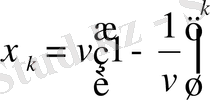
Және бұл байланысты ол арифметикалық прогрессия мен геометриялық
прогрессияның арасындағы байланыс деп ұйғарды. Непер үшін сандар және
олардың логарифмдері бүтін сандар болу керек.
3. Непер ондық логарифмдерді өзінің досы, Лондон университетінің
профессоры Генри Бриггпен (1556-1630) бірлесіп жасады.
Бригг ең әуелі 1-ден 20000–ға дейінгі сандардың, онан кейін 90000–нан
1000000–ға дейінгі сандардың логарифмдерін 14 ондық таңбамен тапты. Ол
құрған ондық логарифмдер таблицалары 1620 жылы жарыққа шықты.
Бригг сандардың ондық логарифмдерін қалай, қандай жолмен тапты, соған
біраз тоқталып кетейік. Егер кез келген саннан біртіндеп түбір таба берсек,
онда ол түбірлер бара – бара 1–ге жуықтаған болар еді. Егер түбір дәрежесі
болса, онда m дәрежелі түбір табу мәселесі квадрат түбірден
біртіндеп n еселі түбір табуға келген болар еді.
Айталық 10 санынан біртіндеп квадрат түбір тауып, өрнегіне жеткен
болайық, әрине, бұл санның ондық логарифмі болады. Былай ұйғарайық:

Бұл теңдіктің екі жағында квадрат дәрежеге шығарсақ онда,

n- санын мейлінше үлкен деп, ал -ны мейлінше аз деп ұйғарсақ
онда - тың мәні нәтиженің ондық таңбасына ешбір әсер етпейді, олай
болса,

Кейінгі теңдіктің екі жағын -ге көбейтсек, онда

Кейінгі жуық теңдікті мына түрде жазуға болады:

Егер былай ұйғарсақ:

Онда санның логарифмінің өзімізге белгілі анықтамасы бойынша

Ал х- тің мәні -не немесе -не тең бе, бәрәбір,
өрнегі бір мәнге ғана ие болады. Сондықтан х – тың саны мен
санының арасындағы мәндері үшін

Егер де түбір табу амалы өрнегіндегі n – нің аса үлкен мәндері
үшін орындалса, онда 1-ге жуық сандардың логарифмдерін табу қиын болмайды.
Жоғарыдағы 1-ге жуық х –ке, кез келген санынан біртіндеп квадрат
түбір табу арқылы келуге болады, яғни

Бұл теңдіктің екі жағын логарифмдеп табатынымыз:

Х-тің және -тің мәндерін (4) теңдікке апарып қойып, мынаны
табамыз.

Сөйтіп кез келген санның ондық логарифмін табу осы саннан және 10-нан
бірнеше рет қайталап квадрат түбір табуға келіп тірелді.
Міне, Бригг сандардың ондық логарифмдерін осы жолмен тапты. Сандардың
ондық логарифмдерінің таблицаларын құрудың оған оңайлықпен түспегенін
мынадан байқауға болады: 10- нан квадрат түбірді ол 54 рет тапқан. Сонда

Бриггтің бастап берген жұмысын әрі қарай созап аяқтаған голланд
математигі Адриан Влакк. Ол 1628 жылы 1-ден 100 000-ға дейінгі сандардың
ондық логарифмдерінің таблицаларын жарыққа шығарды. Тағы да ол Бригг бастан
кеткен тригонометриялық функциялардың ондық логарифмдерінің таблицаларын
құрып аяқтады.

1.2 Логарифмдер және олардың қасиеттері

І-теорема a0, және b0 болатын кез-келген қос нақты a мен b
сандары үшін теңдігі орындалатын x нақты саны табылады және ол жалғыз
болады.
b оң санының a негізі бойынша логарифмі деп, a санының b-ға тең
болатындай дәреже көрсеткішін айтады және оны арқылы белгілейді:
(1)
(І) – негізі логарифмдік тепе-теңдік деп аталады.
теңдігі екенін білдіреді.
Мысалы, өйткені өйткені өйткені
Логарифм тек оң сан үшін және оң бірге тең емес негіз бойынша ғана
анықталатынына оқырманның назарын аударамыз, яғни немесе болатын
кез-келген сандар үшін логарифм түсінігі мағынасынан айырылады. Мысалы: “-8
санының -2 негізі бойынша логарифмі 3 болады” деген сөйлемнің мағынасы
болмайды.
Логарифм анықтамасынан мына теңдіктер шығады:

Жалпы алғанда мына теңдік орын алады:
(2)

Логарифмдердің қасиеттері

болсын. Егер болса, онда:
1)
2)
3) Егер N0, болса, онда егер болса, онда

4) Егер N0, болса, онда

5) Егер болса, онда

6) Егер болса, онда

(берілген негізден басқа негізге көшу формуласы). Дербес жағдайда, егер
c=b болса, онда

7) Егер болса, онда ( белгісі парапар дегенді білдіреді.)

8) Егер болса, онда

яғни логарифм негізі бірден үлкен болса, онда екі оң санның үлкеніне
үлкен логарифм сәйкес келеді және керісінше, үлкен логарифмге үлкен сан
сәйкес келеді.
9) Егер болса, онда

яғни логарифм негізі бірден кіші болса, онда екі оң санның үлкеніне
кіші логарифм сәйкес келеді және керісінше кіші логарифмге үлкен сан сәйкес
келеді.
10) Логарифмдік функцияның анықталу жиыны болып барлық оң сандар жиыны
болады, яғни ол аралығы. Бұл қасиет тікелей логарифмдік функцияның
анықтамасынан шығады.
11) функциясы аралығында a0, үшін кемімелі, ал
үшін өспелі. Расында, болсын.
Онда негізгі логарифмдік тепе-теңдігі бойынша
және теңдіктер орындалады және .
Егер 0a1 болса дәреженің үлкен мәніне t дәреженің кіші мәні
сәйкес келеді, сондықтан . Егер 0a1 болса дәреженің үлкен
мәніне t дәреженің үлкен мәні сәйкес келеді, сондықтан .
12) Логарифмдік функцияның мүмкін мәндерінің жиыны болады. Ол
логарифмдік функцияның монотондығы себебінен кез келген у нақты саны үшін
тек бір ғана сәйкес саны табылады. Онда екені анық.
13) . Расында. . Бұдан кез келген функцияның графигі
(0;1) нүктесі арқылы өтеді. функциясының графигі 0a1 және 1a
болғанда.
14) логарифмдік функциясы мен (мұнда a0, ) көрсеткіш
функциялары өзара кері. Расында, егер , болса, онда және
.
Негізі 10-ға тең логарифмді ондық логарифм деп атайды және мысалы,
орнына деп жазады.
Негізі e санына (e=2,7182818284... иррационал сан) тең логарифмді натурал
логарифм деп атайды және мысалы, орнына деп жазады.
Келесі мысалдарда функцияның жалпы анықтамасына сәйкес берілген
логарифмдік функциялардың әрқайсысын ереже немесе алгоритм ретінде түсінуге
болатынын көрсетейік.
1-м ы с а л функциясы берілсін. Анықтаманы ескере отырып x+10
болатын әрбір x-ке 1 санын қосып оған оның 2 негізді логарифмін сәйкес
қоятын ереже берілген. Сонымен бұл функция аралығында анықталған.
2-м ы с а л функциясы берілсін. Бұл ереже қандай x-терге
қолдануға болатынын анықтайық, яғни 4-3x0, осыдан екені шығады.
Ендеше бұл функция аралығындағы әрбір x санын 3-ке көбейтіп 4 санынан
алып содан шыққан санның 5 негізді логарифмі табылатын ережені анықтайды.
3-м ы с а л Есептеу керек: .
Ш е ш у і: екенін ескеріп дәрежеге шығару қасиетін қолданамыз:

Одан әрі 3), 2) қасиеттерді және теңдігін қолдансақ

аламыз. Сонымен,
4-м ы с а л деп алып, lg25 есептеу керек.
Ш е ш у і
5-м ы с а л деп алып, есептеу керек:
Ш е ш у і 1-тәсіл.
Енді теңдігін пайдаланамыз:

2-тәсіл. деп белгілеп, аламыз. Одан әрі:

Бұдан демек,
6-м ы с а л деп алып, есептеу керек.
Ш е ш у і: деп белгілесек:

Бұдан x-ті тапсақ болады. Олай болса,

7-м ы с а л

Логарифмдеу арқылы:

екенін аламыз, сонда .
Егер болса, онда бұдан мәні берілген теңдеуді
қанағаттандырмайды.
Жауабы: 1; 4
8-м ы с а л

Сондықтан, .
9-м ы с а л
Есептің шартынан

Жауабы:

1.3 Логарифмдік функциялар және олардың қасиеттері

Логарифмдік функцияның пайда болуы мен қалыптасуы Логарифмдерді
енгізгендегі негізгі идея көбейту амалын анағұрлым оңай амалға-қосу амалына
келтіруге болатындығында. Бұл идея сонау ерте заманның өзінде-ақ
математиктерге мәлім болатын. Әсіресе, логарифм теориясының дамуына
Эйлердің еңбектері зор әсер етті. Эйлер логарифмдік функцияларды мұқият
зерттеп, оған көрсеткіштік функцияға кері функция ретінде анықтама береді.
Ол тұңғыш рет логарифмді дәрежеге шығару амалына кері амал деп қарастырды,
яғни Непер дәреже көрсеткіш ұғымы қолдануынан бұрын логарифмді ойлап
шығарды, ал Эйлер логарифм ұғымы дәреже көрсеткіштер ұғымын қарастыруға
байланысты екенін тапты.
Көрсеткішті функцияны анықтап, оны зерттегеннен кейін Эйлер логарифмдік
функцияны келесідей анықтайды: Как по любому значению z может быт найдено
значение y, соответствующему данному числу а, так, и обратно, можно найти
значение переменного z, соответствующее любому заданному положительному
значению переменного у так, чтобы . Это значение переменного z,
поскольку рассматривается как функция у, обычно называется логарифмом
переменного у. Итак, учение о логарифмах предполагает, что вместо а
подставлено определенное постоянное число, которое поэтому носит название
основания логарифмов; когда оно принято, то логарифмом любого числа у будет
показатель степени такой, что ; отсюда понятно, что хотя
основание логарифмов и зависит от нашего выбора, однако оно должно быть
числом, большим, чем единица; отсюда можно получить в виде действительных
чисел только логарифмы положительных чисел.
Логарифм гректің logos – қатынас, arihtmos – сан деген екі сөзінен
құралады. Бұл сөзді осылай құрастырып, алғаш пайдаланған Непер мен Бригтс,
мұнымен олар логарифм екі қатардың (арифметикалық және геометриялық
прогрессиялардың) сәйкес мүшелері арасындағы қатысты көрсететін сан демекші
болғанын түсінуге болады. Логарифмді қысқартудан “log” таңба пайда болды.
Непер логарифмді қысқа символмен белгілемей, оны толық сөзбен жазған.
Характеристика деген термин алғаш Бригтстің Логарифмдік арифметика
деген еңбегінде қолданылады. Мантисса деген сөзді (қосымша, қосалқы
дегенді білдіреді) тұңғыш рет Дж.Валлис өзінің Алгебра (1698) кітабында
ондық бөлшектің бөлшек бөлігін белгілеу үшін қолданған. Ал қазіргі
мағынасында оны Эйлер Анализге кіріспе (1748) еңбегінде пайдаланады, осы
еңбекте Логарифмнің негізі терминді де еңгізеді. Log та4басын 1620ж
Гритер, ал 1624 жылы Кеплер қолданды, ал басқа ғалымдар – L немесе l
әрпімен белгілеген. Эйлер және XVIII ғасырдағы басқа математиктер log не l
таңбасымен белгілейді, ал қазіргі белгілеулер қолданысқа XIX ғасырдың
аяғында еңгізілді.
Айталық, а – оң сан, ол 1-ге тең емес делік.
Анықтама. Мына формуламен берілген
(1)
Функцияны негізі а болатын логарифмдік функция деп атайды.
Логарифмдік функцияның негізгі қасиеттерін атап өтейік.
1. Логарифмдік функцияның анықталу облысы – барлық оң сандар жиыны
яғни
Шынында да, алдыңғы бапта атап көрсетілгендей-ақ әрбір оң x санының a
негізі бойынша логарифмі бар болады.
2. Логарифмдік функцияның мәндерінің облысы – барлық нақты сандар
жиыны.
Шынында да, логарифмнің анықтамасы бойынша кез келген нақты y үшін мына
теңдік орындалады:
(2)
яғни функциясы нүктесінде y0 мәнін қабылдайды:
3. Логарифмдік функция бүкіл анықталу облысында өседі, (a1 болғанда),
не кемиді (0a1 болғанда).
Мысалы, a1 болғанда функцияның өсетінін дәлелдейік (ал 0a1 болғанда
осыған ұқсас түрде пайымдалады).
Айталық, x1 мен x2 – қалауымызша алынған оң сандар және x2x1 болсын.
Сонда болатынын дәлелдеу керек. Кері жориық, яғни былай делік:
(3)
Көрсеткіштік y=ax функциясы a1 болғанда өсетін себепті, (3)
теңсіздіктен мына шығады:

1-сурет

2-сурет
(4)
Ал бірақ та (логарифмнің анықтамасы бойынша), яғни (4)
теңсіздіктен шығады. Ал мұның өзі x2x1 деген ұйғарымға қайшы.
Графигін салу үшін мыналарды еске түсірейік: логарифмдік функция 1
нүктесінде 0 мәніне ие болады; ал кез келген a0 болғанда loga1=0, өйткені
a0=1.
a0 болғанда функция өсетін себепті, x1 болғанда логарифмдік функция
оң мәндерді қабылдайды да, ал 0x1 болғанда – теріс мәндерді қабылдайды.
Егерде 0a1 болса, онда жиында кемиді, сондықтан 0x1
болғанда және x1 болғанда .
Дәлелденген қасиеттерге сүйеніп, функцияның a1 болғандағы (1, a-
сурет) және 0a1 болғандағы (1, б-сурет) графигін салу қиын емес.

3-сурет
Мынадай тұжырым дұрыс:
Негізі бірдей болып келген көрсеткіштік және логарифмдік функциялардың
графиктері y=x түзуіне қатысты симметриялы болады (2-сурет).
Логарифмдік функциялардың қасиеттері қолданылатын мысалдарды
қарастырайық[4].
1-м ы с а л Мына функцияның анықталу облысын табайық:

Логарифмдік функцияның анықталу облысы – R+ жиыны. Сондықтан берілген
функция тек 4-5x0 шарты орындалатындай x мәндерінде ғана анықталған, яғни
x0,8. Олай болса, берілген функцияның анықталу облысы интервалы.
2-м ы с а л Мына функцияның анықталу облысын табайық:

Алдыңғы мысалдағы сияқты, f функциясы x2-3x-40 шарты орындалатындай
барлық x мәндерінде анықталған. Осы квадрат теңсіздікті шешіп, D(f)
дегеніміз мен интервалдарының бірігуі екенін табамыз.
3-м ы с а л Мына функцияның анықталу облысын табайық:

теңсіздігін интервалдар әдісімен шешіп, екенін табамыз (3-
сурет).

Функцияның анықталу аймағы – R барлық нақты сандар жиынтығы.
Функцияның жиынтық мағынасы – R+ барлық оң сандар жиынтығы:
, кез келген нақты мәні.
болғанда функция өспелі,егер болса,онда ,ал
болғанда функция кемімелі,егер болса,онда болады.
Егер болса,онда
Логарифмдік функцияның қасиеттері:

Функцияның анықталу аймағы – R+ барлық оң сандар жиынтығы.
Функцияның жиынтық мағынасы – R барлық нақты сандар жиынтығы.
болғанда функция өспелі,егер болса,онда , ал
болғанда функция кемімелі,егер болса,онда болады.
Логарифмдер қасиеттері:
Егер болса, онда (негізгі логарифмдік теңбе-теңдік).
Логарифмнің негізі 1-ге тең: .

Егер және болса,онда (логарифмдердің
көбейтіндісінің формуласы).
(логарифмдердің бөліндісінің формуласы).
Егер болса, онда , мұндағы кез келген нақты сан
(логарифмдердің дәрежелік формуласы).
Егер болса, онда кез келген нақты сан
(логарифмдердің жаңа негізге өту формуласы). Сонымен қатар,

Көрсеткіштік және логарифмдік теңдеулер үшін ескертулер.
Көрсеткіштік (1) теңдеуді логарифмдегенде мынау теңдеу
келіп шығады:. (2) Сондықтан, теңдігі теңдігімен теңбе-
тең.
(3) теңдеуінің түбірі аралас жүйеде ғана шешімін табады.
Яғни, (4)
Логарифмдік (5) теңдігі (6) теңдігімен теңбе-тең.
(7) логарифмдік теңдеу мына әрбір жүйелермен теңбе-тең:
немесе (8)
теңдеуін шешу үшін тек бір жүйені ғана шешу жеткілікті (екіншісі
оңайлау) немесе теңдеуін шешеміз, теңдеудің табылған түбірін әрбір
теңдеудің орнына қойып тексереміз.

теңдеудерін шешу үшін логарифмдердің көбейтіндісі мен бөліндісінің
формуласын пайдаланып мына түрге келтіреміз:

арықарай теңдеуді қасиет бойынша шығарамыз. Табылған түбірлерді
орнына қойып тексереміз.
Егер теңдеуді логарифмдердің көбейтіндісі мен бөліндісінің
формуласын пайдаланып шешсек, мына түрге айналдыру керек болады: ,
мұндағы жұп сан, олай болса берілген теңдеудің түбірі жоғалып кетеді.
Мұндай жағдайда түбірді сақтап қалу үшін, мына формуланы пайдаланамыз:

11-м ы с а л Логарифмдік функцияның қасиеттерін пайдаланып келесі
сандарды салыстырайық:
a) және
Негізі 1-ден үлкен логарифмдік функция бүкіл сандық түзуде өседі, олай
болса 94 болғандықтан .
b) және
Ал негізі 1-ден кіші логарифмдік функция бүкіл сандық түзуде кемиді,
олай болса 117 болғандықтан .
c) және
Логарифмнің монотондылық қасиетін негіздері бірдей логарифмдерге
қолдану арқылы төмендегі теңсіздіктерді жазуға болады:
, ал , олай болса .
12-м ы с а л Функцияның графигін салыңыздар:
a)
Логарифмдік функцияның графигін қарастырғанбыз. Тек бұл мысалда негізі
2-ге тең дербес жағдайы үшін салайық. -ге 3 саны қосылғандықтан
графигін Oy өсі бойынша 3 бірлікке жоғары параллель көшіреміз.

4-сурет

b)
Бұл жағдайда да негізі ге тең логарифдік функцияның графигін
салайық. Енді функцияның берілуі мына түрде болғандықтан салынған
графикті Ox өсі бойынша 2 бірлікке оңға параллель көшіреміз.

5-сурет
2 Логарифмдік теңдеулер мен теңсіздіктерді шешу

2.1 Қарапайым логарифмдік теңдеулер

Ең қарапайым логарифмдік теңдеуді қарастырайық . Логарифмдік
функция аралығында өседі (не кемиді) және осы аралықта барлық нақты
мәндерді қабылдайды. Түбір туралы теорема бойынша, бұдан кез келген b үшін
берілген теңдеудің түбірі бар және ол тек біреу ғана болатындығы шығады.
Санның логарифмінің анықтамасынан саны сол шешім екендігі бірден
табылады.
1-м ы с а л Теңдеуді шешейік .
Берілген теңдеуді x-тің теңдігі орындалатындай мәндері ғана
қанағаттандырады. Сонымен, x2+4x-5=0 квадрат теңдеу шықты. Оның түбірлері:
1 мен -5 сандары. Олай болса, берілген теңдеудің шешімі екі сан, олар: 1
мен -5.
2-м ы с а л Теңдеуді шешейік
Бұл теңдеу x-тің тек 2x+30 және x+10 теңсіздіктері орындалатындай
мәндерінде ғана анықталады. x-тің мәндері үшін берілген теңдеу 2x+3=x+1
теңдеуімен мәндес. Бұдан x=-2 екенін табамыз. Ал x=-2 саны x+10
теңсіздігін қанағаттандырмайды. Олай болса, берілген теңдеудің түбірлері
болмайды.
Ал осы теңдеуді басқаша шешуге болар еді. Берілген теңдеудің салдарына
2x+3=x+1 ауысып, x=-2 екенін табамыз. Теңдеулерді мәндестік бұзылмайтындай
етіп түрлендірген жағдайда, табылған мәнді бастапқы теңдеуге қойып, тексеру
қажет. Тап осы жағдайда теңдігі тура емес (мұның мағынасы жоқ).
3-м ы с а л Теңдеуді шешейік
Бұл теңдеуді x-тің тек x0 және (x – логарифмдік функцияның
негізі) және x2-2x+2=x, яғни x2-3x+2=0 теңдігі орындалатындай мәндері ғана
қанағаттандырады. Осы табылған квадрат теңдеудің түбірлері 1 және 2 сандары
болып табылады. Алайда x=1 саны берілген теңдеудің шешімі бола алмайды.
Олай болса, тек 2 саны ғана берілген теңдеудің шешімі болады.
4-м ы с а л Теңдеуді шешейік
Енді қосылғышты 5 негізіне көшіріп, ауыстыруын жасаймыз, сонда
.
Енді берілген теңдеуді t2-2t-3=0 түрінде көшіріп жазуға болады. Бұл
квадрат теңдеудің, түбірлері 3 және -1 сандары. Ауыстырылғаннан кейінгі
log5x=3 және log5x=-1 теңдеулерін шешіп, мынаны табамыз: x=53=125 және x=5-
1=0,2.
5-м ы с а л Теңдеулер жүйесін шешейік:

Жүйенің бірінші теңдеуі y-x=2 теңдеуімен, ал екіншісі теңдеуімен
мәндес және x0, y0. ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.