Математикалық өрнектерді теңбе-тең түрлендіру және мектепте оқыту әдістемесі


МАЗМҰНЫ
Кіріспе . . . 3
1 Математикалық өрнектер. Математикалық өрнектерді теңбе-тең
түрлендіру.
1. 1 Әріпті өрнектер және оларды теңбе-тең түрлендіру . . . 6
1. 2 Рационал өрнектерді теңбе-тең түрлендіру…… . . . 10
1. 3 Иррационал өрнектерді теңбе-тең түрлендіру . . . 21
1. 4 Трансцендент өрнектер . . . 26
2 Теңбе-тең түрлендіруді оқытудың әдістемесі.
2. 1 Теңбе-тең түрлендіруді мақсатты орындау туралы . . . 49
2. 2 Теңбе-тең түрлендіруді оқыту кезінде саналылық принципін
жүзеге асыру . . . 52
- Мектеп математика курсында теңбе-теңдік ұғымын
енгізу туралы . . . 57
Қорытынды . . . 61
Пайдаланылған әдебиеттер тізімі . . . 62
Аннотация
Мектеп математика курсында өрнектер және оларды теңбе-тең түрлендіру тақырыбы жеке тақырып қана емес, ол математиканың бүкіл өн бойында оқытылады. Математикалық өрнектерді теңбе-тең түрлендіруді оқушылардың санасына терең сіңіру әрі тиімді әдістер мен тәсілдерді пайдаланып шешуді үйрету мұғалімнің басты мақсаты болып табылады. Өрнектердің түрлерін ажырата білуге және оларды теңбе-тең түрлендіру әдістемесіне баса назар аударылуы керек. Теңбе-тең түрлендіруде оқушылардың жіберген қателерімен жұмыс істеу арқылы олардың қызығушылығын арттыруға болады. Яғни, оқушы тақтаға өрнектің берілгенін қате жазса, онда сабақтың біраз уақыты заяға кетеді. Сондықтан мұнда мұғалім тарапынан ұтымды әдістерді пайдалану қажеттілігі туындайды.
Дипломдық жұмыс кіріспеден, екі бөлімнен қортындыдан және пайдаланылған әдебиеттер тізімінен тұрады.
Кіріспе
Жұмыстың өзектілігі. Математикалық өрнектерді теңбе-тең түрлендірулер мектеп матиматика курсындағы ең басты мазмұнды-әдістемелік бағыттардың бірі болып табылады. Олардың негізінде оқушыларда математиканы оқытудағы аналитикалық тәсілдер қалыптасады. Әдетте, әрбір математикалық есепті аналитикалық тәсілмен шешу қандай да бір теңбе-тең түрлендіруді қажет етеді. Теңбе-тең түрлендірулер мектеп математикасының жеке тақырыбы емес, олар алгебра мен математикалық анализ курсы бастамаларының бүкіл өн бойында оқытылады.
Алдымен, оқушыларға «математикалық өрнектің» өзі не екенін түсіндіруіміз, анықтамасымен таныстыруымыз қажет. Содан «өрнекті түрлендіру» мен оны «теңбе-тең түрлендіру» және оның оқыту әдістемесін жүйелі түрде үйретуіміз тиіс. Енді осыларға жеке-жеке анықтама беріп, нақтылаймыз:
Математикалық өрнек-сандар және айнымалылардан (әріптерден) құралған, амалдар белгілерімен немесе функциялармен және жақшалармен байланысқан кез келген жазба. Өрнектің формула немесе оның бөлігі болуы да мүмкін. Өрнекте әріптік айнымалы шамалардың болу немесе болмауына тәуелді түрде өрнектер сан өрнектер және айнымалы бар өрнектер болып екіге ажыратылады.
Өрнекті түрлендіру деп - жиынды өзіне бейнелеу, белгілі бір мақсат үшін бір формуладан (теңбе-теңдіктен) немесе координаттар жүйесінен ыңғайлырақ өзге түрге ауысуды айтады.
Теңбе-тең түрлендіру- бір аналтикалық өрнекті оған теңбе-тең, бірақ сырт түрі өзгеше болып келген өрнекпен ауыстыру. Теңбе-тең түрлендірудің мақсаты өрнекке сандық есептеулерді жүзеге асыруа ыңғайлы ету үшін немесе логарифмдеу, потенцирлеу, диференциалдау, интегралдау, теңдеулер шешу т. б. амалдарды оңайлату үшін әрі қарай түрлендірулер жасау болп табылады. Ұқсас мүшелерді біріктіру, жақшаларды ашу, көбейткіштерге жіктеу, алгебралық бөлшектерді ортақ бөлімге келтіру және оларды қарапайым бөлшектерге жіктеу, тригонометриялық функциялардың қосындыларын логарифмдеуге ыңғайлы түрге келтіру(яғни оларды көбейтіндіге түрлендіру) теңбе-тең түрлендіруге жатады.
Теңбе-теңдік математикалық екі өрнектің өзіне қамтылған әріптердің мүмкін мәндерінде тура болу теңдігі. Теңбе-теңдік «
 » белгісін 1857 жылы неміс математигі Георг Риман(1826-1866) ұсынған.
» белгісін 1857 жылы неміс математигі Георг Риман(1826-1866) ұсынған.
Алгебра оқулықтарында теңбе-теңдік ұғымының әртүрлі анықтамалары қолданылады:
- Айнымалының кез келген мәндерінде дұрыс болатын теңдікті теңбе-теңдік деп атайды;
- Айнымалының барлық мәндерінде дұрыс болатын теңдікті теңбе-теңдік деп атайды;
- Айнымалының берілген жиынға тиісті кез келген мәнінде дұрыс болатын теңдікті осы жиында теңбе-теңдік деп атайды.
Теңбе-теңдік 1 түрдегі анықтамасының салдары 2 және 3-ші түрдегі анықтамалар болатындығын байқау қиын емес. Кері тұжырым барлық уақытта бірдей орындала бермейді. Бұл келтірілген анықтамалардың өзара мәндес еместігін көрсетеді.
Теңбе-теңдіктің құндылығы мынада: ол берілген өрнекті оған мәндес бір өрнекпен, оны оған мәндес үшінші өрнекпен т. с. с. ауыстыруға мүмкіндік береді. Басқаша айтқанда, транзитивтік қасиетке ие: егер А мен В және В мен С теңбе-тең болса, онда А мен С да тең болады.
Алгебрелық өрнектерге қолданылатын амалдардың екі түрлі түсіндірмесі (трактовкасы) болуы мүмкін.
Бірінші түсіндірме (трактовка) абстрактылы алгебраның көзқарасын бейнелейді. Белгілі бір алгебралық операцияны алу үшін берілген өрнектердің арасына сәйкес амалдың таңбасын қою жеткілікті, нәтижеде берілген екі өрнекке тек бір ғана үшінші өрнек сәйкес келетін болып шығады. Өрнектердің арасына амал белгісі қойылғанда ғана амал орындалған болып есептеледі. Егер кейінгі теңбе-тең түрлендірулер орындалатын болса, нәтижеде шығатын қосындыны (айырма, көбейтінді, бөлінді) түрлендіру емес, жазылған қосындыны (айырма, көбейтінді, бөлінді) түрлендіру болып табылады. Түрлендіру алгебралық заңдылықтарды формальді түрде қолдану арқылы жүзеге асырылады.
Екінші түсіндірме (трактовка) функционалдық талдаудың көзқарасын бейнелейді, бұл көзқарас бойынша екі көпмүшелікті қосу үшін оларды формальді түрде «+» белгісімен (таңбасымен) біріктіру жеткіліксіз (бұл өрнекке енетін айнымалының барлық мәндерінде), шыққан өрнектің мәнінің қосылғыш өрнектердің қосындысының мәніне тең болатындығына көз жеткізу керек. Сондықтан да болар бірінші трактовка бойынша «екі өрнектің қосындысын (айырымын, көбейтіндісін, бөліндісін) табыңдар» деген бағалы жаттығулар өте аз кездеседі. Алгебра оқулықтарында оның орнына мынадай жаттығулар келтіріледі: «өрнекті ықшамдаңдар», «азайту амалына қатысты көбейтудің үлестірімділік заңын пайдаланып теңбе-тең өрнекке түрлендіріңдер», «жақшаны ашыңдар», т. с. с.
Алгебралық өрнектерді жеке дара бөліп алып қарастырмай, оларды белгілі бір сандық жиында қарастыру, сандық өрнектердің жазылуының жалпылануы деп түсінгенде ғана оқушылар теңбе-тең түрлендірулерді саналы түрде меңгере алады. Алгебралық және сандық өрнектердің арасындағы ұқсастық логикалық тұрғыдан алып қарағанда заңды, оларды оқытуда қолдану оқушылардың қателерді жібермеуіне септігін тигізеді.
Дипломдық жұмыстың мақсаты: математикалық өрнектерді қайсы сыныпта, қандай көлемде оқытылатынына тәуелсіз мазмұнды-әдістемелік бағыттар бойынша оқыту әдістемесін жүйелеу.
Зерттеу пәні: математикалық өрнектерді теңбе-тең түрлендіру әдістері.
Зерттеу нысаны: математика курсын оқытуда математикалық өрнектерді теңбе-тең түрлендіруге оқытудың әдістемесі.
Дипломдық жұмыстың әдіснамалық негізі:
- зерттелетін тақырып бойынша математикалы ғылыми-әдістемелік, психологиялық-педагогикалық, философиялық әдебиеттерге талдау жүргізу;
- орта білім мен математикалық деңгейі туралы нормативтік құжаттарды талдау;
- математика мұғалімдерінің алдыңғы қатарлы тәжірибесін оқу және жалпылау.
Зерттеу жұмысының міндеті:
- математикалық өрнектердің анықтамасы мен олардың арасындағы байланысты білу;
- әріпті өрнектер, рационал және иррационал, трансценденттік өрнектерді теңбе-тең түрлендіруді оқытудың әдістемесін меңгеру;
- теңбе-тең түрлендіруді мақсатты орындау туралы, саналылық принципін жүзеге асыру, оқушылардың жіберген қатесімен жүргізілетін жұмыстар, теңбе-теңдік ұғымын еңгізу әдістемелерін саналы түрде игеру.
Зерттеудің ғылыми жаңалығы:
1 Математикалық өрнектер. Математикалық өрнектерді
теңбе-тең түрлендіру
- Әріпті өрнектер және оларды теңбе-тең түрлендіру.
М ы с а л Ұзындығы 7 см, ені 3 см тік төртбұрыштың ауданы
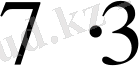 санды өрнегімен жазылады.
санды өрнегімен жазылады.
Егер a=7 см, b=3 см болса, тік төртбұрыштың ауданы
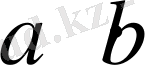 әріпті өрнегімен жазылады.
әріпті өрнегімен жазылады.
5x+3; 0, 7x; a;
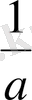 ;
;
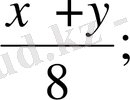
 ; 2(a+b) - бұлар әріпті өрнектер.
; 2(a+b) - бұлар әріпті өрнектер.
Құрамында бір немесе бірнеше әрпі бар өрнекті әріпті өрнек деп атайды.
Формулалар мен есептің шартына байланысты құрылған теңдеулерді жазуда әріпті өрнектер пайдаланылады.
Әріпті өрнектің жазылуында әріптер болуымен қатар, сандар, жақшалар және арифметикалық амалдар таңбалары да болуы мүмкін.
Кейде бір әріптің өзі де әріпті өрнек бола алады, Мысалы b - әріпті өрнек, x - әріпті өрнек.
Әріпті өрнектерді жазуда ескерілетін ережелер мен келісілген шарттар бар.
1 Әріпті өрнекте (көбейтіндіде) сан көбейткіш әріп көбейткіштің алдына жазылады. Сан көбейткіш пен әріп көбейткіштің арасына көбейту таңбасы қойылмайды.
Көбейтіндідегі сан көбейткішті әріп көбейткіштің алдына жазып, оны коэффициент деп атайды.
Коэффициент пен одан кейінгі әріп көбейткіштің арасына көбейту таңбасы қойылмайды.
Мысалы
 немесе
немесе
 әріпті өрнегін
9a
түрінде жазуды білеміз.
әріпті өрнегін
9a
түрінде жазуды білеміз.
Сол сияқты,
 немесе
немесе
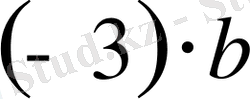 әріпті өрнегі
-3b
түрінде жазылады.
әріпті өрнегі
-3b
түрінде жазылады.
2 Әріпті өрнектегі әріп көбейткіштердің арасына көбейту таңбасы қойылмайды.
Мысалы
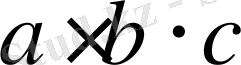 әріпті өрнегі abc түрінде жазылады.
әріпті өрнегі abc түрінде жазылады.
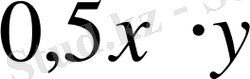 әріпті өрнегі 0, 5xy түрінде жазылады.
әріпті өрнегі 0, 5xy түрінде жазылады.
3 Құрамында әріптері бар бөлінді бөлшек түрінде жазылады.
Мысалы
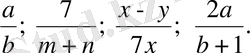
4 Әріпті өрнектердің жазылуында жақшаны пайдалануға ерекше назар аудару қажет.
Мысалы x санынан y пен 9 санының қосындысын азайтуды өрнек түрінде былай жазады: x-(y+9) . Егер өрнекті осы қалпында жақшасыз жазсақ, x-y+9 әріпті өрнегі шығады. Соңғы өрнектегі амалдар реті алғашқы қойылған шартқа сәйкес емес. x-y+9 әріпті өрнегінде x санынан y санын азайтып, нәтижесінде 9 санын қосу керек. Демек, бұл жағдайда жақшасыз жазуға болмайды.
Мысалы 10 санына x пен y сандарының көбейтіндісін қосуды өрнек түрінде жазайық: 10+xy.
Бұл жағдайда x пен y сандарының көбейтіндісін жақша ішіне жазудың қажеті жоқ. Себебі амалдардың орындалу тәртібі бойынша көбейту амалы алдымен орындалып, өрнектің құрылу шарты сақталады.
Әріпті өрнектің сан мәнін табуды қарастырайық.
Әріпті өрнектегі әріптің орнына өрнектің мағынасы болатындай оның сан мәнін қойып есептеуге болады.
Бұл әріпті өрнектің қасиеті.
Әріпті өрнектердегі әріптер әр түрлі сан мәндерді қабылдай алады. Сондықтан әріпті өрнектегі әріп айнымалы деп аталса, әріпті өрнектің өзі айнымалысы бар өрнек деп аталады.
Мысалы 2(a+b) - айнымалысы бар өрнек, мұндағы a және b - айнымалылар.
Әріпті өрнектегі әріпті оның сан мәнімен алмастыруды әріпті өрнектің сан мәнін қою деп атайды.
Мысалы
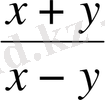 әріпті өрнегіне оның x=9; y=-3 сан мәндерін қойсақ,
әріпті өрнегіне оның x=9; y=-3 сан мәндерін қойсақ,
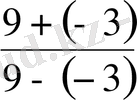 санды өрнегі шығады.
санды өрнегі шығады.
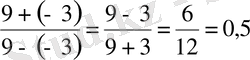 , 0, 5 - берілген
, 0, 5 - берілген
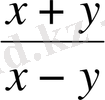 әріпті өрнегінің x=9; y=-3 болғандағы сандық мәні.
әріпті өрнегінің x=9; y=-3 болғандағы сандық мәні.
Әріпті өрнектің сандық мәнін табу үшін:
1 әріпті өрнектегі әріптерді олардың сан мәндерімен алмастыру қажет;
2 әріпті өрнектегі бірдей әріптер бірдей санмен алмастырылады (ұқсас мүшелері біріктірілмеген жағдайда) ;
3 теріс сандар жақша ішіне алынып жазылады;
4 әріпті өрнектегі жақшалар есепке алынып (егер жақша болса), тиісті арифметикалық амалдар рет-ретімен орындалады;
5 әріпті өрнек бөлшек түрінде берілсе, оның алымының және бөлімінің сандық мәндері жеке-жеке табылып, содан соң олардың бөліндісі табылады.
Мысалы
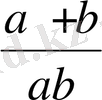 , мұндағы a мен b - айнымалылар,
, мұндағы a мен b - айнымалылар,
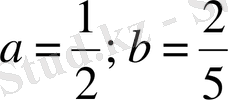 болғанда:
болғанда:
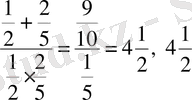 - өрнектің сандық мәні.
- өрнектің сандық мәні.
Әріпті өрнектегі әріптердің орнына олардың берілген сан мәндерін қойып, көрсетілген амалдарды орындау нәтижесінде шыққан сан әріпті өрнектің сандық мәні болады.
Берілген әріпті өрнектегі әріп сол өрнектің мағынасы болатын санмен ғана алмастырылады.
Мысалы
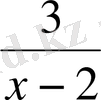 әріпті өрнегінде x-тің орнына 2 санын қоюға болмайды. Себебі x=2 мәнінде
әріпті өрнегінде x-тің орнына 2 санын қоюға болмайды. Себебі x=2 мәнінде
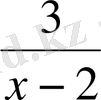 бөлшегінің бөлімі 0-ге тең. Ал 0-ге бөлуге болмайды. Онда берілген әріпті өрнектегі
бөлшегінің бөлімі 0-ге тең. Ал 0-ге бөлуге болмайды. Онда берілген әріпті өрнектегі
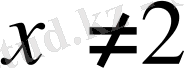 . Демек, x-тің сан мәні 2-ге тең болса,
. Демек, x-тің сан мәні 2-ге тең болса,
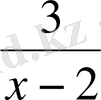 әріпті өрнегінің мағынасы болмайды.
әріпті өрнегінің мағынасы болмайды.
Бұл жағдайда
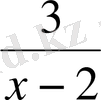 әріпті өрнегіндегі айнымалы x-тің қабылдайтын мәндерінің жиыны 2 санынан басқа барлық сандар. Жазылуы:
әріпті өрнегіндегі айнымалы x-тің қабылдайтын мәндерінің жиыны 2 санынан басқа барлық сандар. Жазылуы:
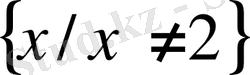 немесе
немесе
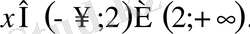
Әріптің берілген әріпті өрнектің мағынасы болатын сан мәндерін сол әріпті өрнектегі әріптің қабылдайтын сан мәндері деп атайды.
Әріпті өрнектердің сандық мәндерін (ең тиімді тәсілмен) табу үшін, әріпті өрнекті ықшамдау керек.
Әріпті өрнекті ықшамдау оны теңбе-тең өрнекке түрлендіру арқылы орындалады.
Мысалы a(b+8) және ab+8a өрнектері теңбе-тең өрнектер, егер a=3, b=2, 1 болса,
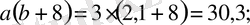
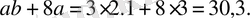
Әріптердің a=3, b=2, 1 мәндерінде a(b+8) және ab+8a өрнектерінің сандық мәндері (30, 3) өзара тең. Мұндай өрнектер теңбе-тең өрнектер деп аталады.
Теңбе-тең әріпті өрнектер дегеніміз - олардағы әріптердің тең (бірдей) мәндерінде сандық мәндері тең (бірдей) болатын әріпті өрнектер.
Өрнектерді түрлендіргенде, әріпті өрнек ықшамдалып, алғашқы әріпті өрнекпен теңбе-тең өрнек пайда болады.
Өрнекті оған теңбе-тең өрнекпен алмастыруды өрнекті теңбе-тең түрлендіру немесе өрнекті түрлендіру деп атайды.
І Қосудың ауыстырымдылық және терімділік қасиеттерін пайдаланып, әріпті өрнектегі алгебралық қосылғыштардың орындарын ауыстырып топтастырғанда әріпті өрнек теңбе-тең өрнекке түрленіп, ықшамдалады.
Мысалы
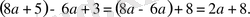
Мұндағы 2a+8 өрнегі - алғашқы (8a+5) -6a+3 өрнегінің ықшамдалған түрі.
II Көбейтудің ауыстырымдылық және терімділік қасиеттерін пайдаланып, әріпті өрнектегі көбейткіштердің орындарын ауыстырып, топтастырғанда әріпті өрнек теңбе-тең өрнекке түрленіп, ықшамдалады.
Мысалы
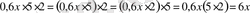 .
.
Мұндағы 6x өрнегі алғашқы
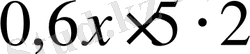 өрнегінің ықшамдалған түрі.
өрнегінің ықшамдалған түрі.
III Көбейту амалының қосуға (азайтуға) қатысты үлестірімділік қасиетін пайдаланып, әріпті өрнектерді ықшамдау.

Мұндағы a(b+c) әріпті өрнегі мен ab+ac әріпті өрнегі теңбе-тең өрнектер.
1-мысал
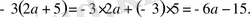
Мұндағы -6a-15 өрнегі - алғашқы -3(2a+5) өрнегінің ықшамдалған түрі.
2-мысал
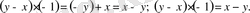
x-y өрнегі - алғашқы
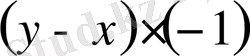 өрнегінің ықшамдалған түрі.
өрнегінің ықшамдалған түрі.
IV Қосындыны берілген санға бөлуді пайдаланып, әріпті өрнекті ықшамдау.
Қосындыны берілген санға бөлгендегі бөлінді қосылғыштарды жеке-жеке берілген санға бөлгендегі бөлінділердің қосындысына тең (5-сынып) .
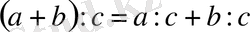 немесе
немесе
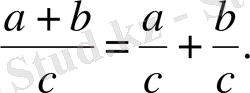
Демек,
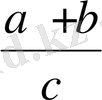 бөліндісін бөлімдері бірдей
бөліндісін бөлімдері бірдей
 және
және
 бөлшектерінің қосындысы түрінде теңбң-тең түрлендіріп ықшамдауға болады.
бөлшектерінің қосындысы түрінде теңбң-тең түрлендіріп ықшамдауға болады.
Мысалы
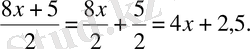
 әріпті өрнегі - алғашқы
әріпті өрнегі - алғашқы
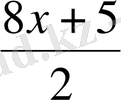 өрнегінің ықшамдалған түрі.
өрнегінің ықшамдалған түрі.
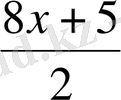 және
және
 өрнектері - теңбе-тең өрнектер.
өрнектері - теңбе-тең өрнектер.
V Әріпті өрнектерді қысқартуды пайдаланып ықшамдау.
Егер бөлшектің алымының да, бөлімінің де бірдей әріп көбейткіштері болса, бөлшектердің негізгі қасиетін пайдаланып, бөлшектерді қысқартады.
Қысқартылғанға дейінгі бөлшек қысқартылғаннан кейінгі бөлшекпен теңбе-тең болады. Бөлшектердің алымы да, бөлімі де олардың ортақ әріп көбейткіштеріне (егер бар болса) қысқартылып ықшамдалады.
Мысалы
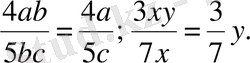
Мұндағы
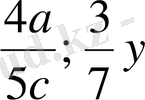 - алғашқы өрнектердің ықшамдалған түрі.
- алғашқы өрнектердің ықшамдалған түрі.
І Әріпті өрнектердегі жақшаны ашып түрлендіру. Көбейтудің үлестірімділік қасиетін пайдаланып жақшаны ашу.
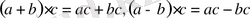 .
.
Көбейтудің үлестірімділік қасиеті жақша ішіндегі қосылғыштар санына тәуелсіз. Сондықтан жақша ішіндегі алгебралық қосылғыштар саны екіден көп болған жағдайда да жақшаны ашу үшін көбейтудің үлестірімділік қасиеті пайдаланылады:
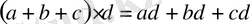 .
.
1-мысал

Жақша алдында «+» таңбасы болса, жақшаны ашқанда жақша ішіндегі алгебралық қосылғыштардың өз таңбалары сақталады.
2-мысал
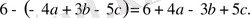
Әріппен жазсақ
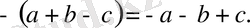
Жақшаның алдында «-» таңбасы болса, жақшаны ашқанда, жақша ішіндегі алгебралық қосылғыштардың таңбаларын қарама-қарсы таңбалармен алмастыру керек.
II Әріпті өрнектегі ортақ көбейткішті жақша сыртына шығарып түрлендіру.
Егер әріпті өрнектегі алгебралық қосылғыштардың құрамында ортақ көбейткіш бар болса, онда оны жақшаның сыртына шығарып, әріпті өрнекті түрлендіруге болады.
3-мысал
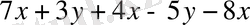 өрнегіндегі ортақ көбейткіштерді жақша сыртына шығарып түрлендірейік. Берілген өрнектегі 7x; 4x және -8x - ұқсас қосылғыштар, олардың ортақ көбейткіші x. 3y және -5y - ұқсас қосылғыштар, ортақ көбейткіші y.
өрнегіндегі ортақ көбейткіштерді жақша сыртына шығарып түрлендірейік. Берілген өрнектегі 7x; 4x және -8x - ұқсас қосылғыштар, олардың ортақ көбейткіші x. 3y және -5y - ұқсас қосылғыштар, ортақ көбейткіші y.
Ұқсас қосылғыштардағы ортақ көбейткіштерді жақша сыртына шығарып түрлендірсек:
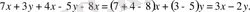
Өрнектегі ұқсас қосылғыштарды біріктіру арқылы түрлендірдік. Кейде өрнектегі ұқсас қосылғыштарды ұқсас мүшелер деп те атайды. Сондықтан әріпті (айнымалысы бар) өрнектердегі ұқсас қосылғыштар ұқсас мүшелер деп аталып, оларды алгебралық қосу ұқсас мүшелерді біріктіру деп те аталады. Мұндай түрлендіруді әріпті өрнектерді ықшамдауда пайдалану керек.
III. Әріпті өрнектерді жақшаға алып түрлендіру.
Әріпті өрнектерді жақшаға алғанда
1 Жақша алдына «+» таңбасы қойылса, жақша ішіне әріпті өрнектегі мүшелердің таңбаларын өзгертпей алу керек.
4-мысал
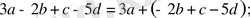
Әріппен жазсақ,
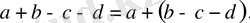
2 Жақша алдына «-» таңбасы қойылса, жақша ішіне әріпті өрнектегі мүшелердің таңбаларын қарама-қарсы таңбаға өзгертіп алу керек.
5-мысал
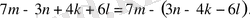
Әріппен жазсақ:
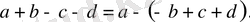
6-мысал
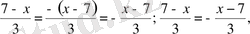 сол сияқты,
сол сияқты,
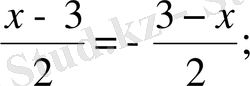
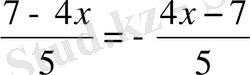 [3] .
[3] .
1. 2 Рационал өрнектерді теңбе-тең түрлендіру
Сандар мен айнымалдарға қосу, азайту, көбейту, бөлу, рационал дәрежеге шығару, түбір табу және жақшаға алу амалдарын қолдана отырып алгебралық өрнектер құрауға болады.
Мысалы
1)
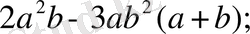 2)
2)
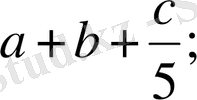 3)
3)
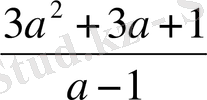
4)
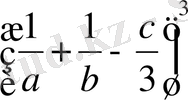 5)
5)
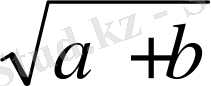 6)
6)
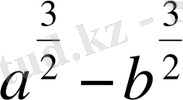
Құрамындағы айнымалдарға тек қосу, азайту, көбейту, бөлу және бүтін дәрежеге шығару амалдарын ғана қолданып, алынған алгебралық өрнекті рационал өрнек деп атайды.
Жоғарыдағы мысалдарда 1), 4) және 6) - рационал өрнектер.
Рационал өрнектің бөлімінде айнымалдар жоқ болса ол бүтін өрнек, ал бөлімінде айнымалдар бар болса - бөлшек өрнек деп аталады. Жоғарыдағы мысалдарда 1) , 2) және 6) - бүтін, ал 3) пен 4) - бөлшек өрнектер.
Алгебралық өрнекті ең соңғы амалдың нәтижесімен атайды .
Мысалы
1)
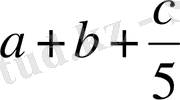 - қосынды;
- қосынды;
2)
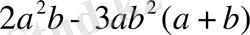 - айырма (айырманы қосынды түріне келтіруге болғандықтан, оны қосынды деп те атай береді) ;
- айырма (айырманы қосынды түріне келтіруге болғандықтан, оны қосынды деп те атай береді) ;
3)
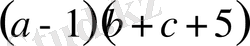 - көбейтінді;
- көбейтінді;
4)
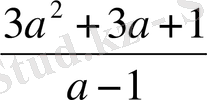 - бөлінді (бөліндіні көбейтінді түрінде жазуға болғандықтан, оны көбейтінді деп та атай береді) ;
- бөлінді (бөліндіні көбейтінді түрінде жазуға болғандықтан, оны көбейтінді деп та атай береді) ;
Өрнекті теңбе-тең түрлендіру
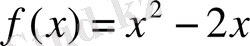 және
және
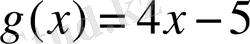 өрнектерін қарастырайық. Мысалы, х=2 тең болса,
өрнектерін қарастырайық. Мысалы, х=2 тең болса,
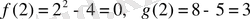 аламыз. Осы 0 және 3 сандарын
аламыз. Осы 0 және 3 сандарын
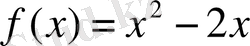 және
және
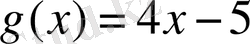 өрнектерінің х=2 -ге сәйкес мәндері деп атайды.
өрнектерінің х=2 -ге сәйкес мәндері деп атайды.
Берілген өрнектердің анықталу аймақтарының ортақ бөлігін (қиылысуын) осы өрнектердің анықталу аймағы деп атаймыз.
Х - берілген өрнектердің анықталу аймағының ішкі жиыны болсын. Егер осы өрнекердің Х жиынының әрбір элементіне сәйкес келетін мәндері бірдей болса, онда олар Х жиынында теңбе-тең өрнектер деп аталады.
Теңбе-теңдік деп, құрамындағы айнымалдардың барлық мүмкін мәндерінде дұрыс болатын теңдікті айтады.
Мысалы,
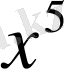 пен
пен
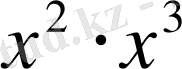 ,
,
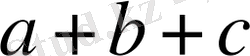 мен
мен
 ,
,
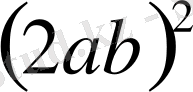 пен
пен
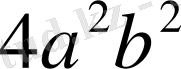 - айнымалдардың кез келген мәндер жиынында теңбе-тең өрнектер.
- айнымалдардың кез келген мәндер жиынында теңбе-тең өрнектер.
Теңбе-теңдіктер:
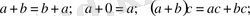 ал
ал
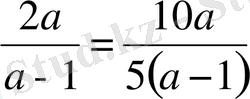 теңдігі
теңдігі
 ның барлық мүмкін мәндерінде, яғни,
ның барлық мүмкін мәндерінде, яғни,
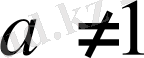 мәндерінде теңбе-теңдік болады.
мәндерінде теңбе-теңдік болады.
Өрнекті оған теңбе-тең басқа өрнекпен ауыстыру - өрнекті теңбе-тең түрлендіру деп аталады.
Бірмүшеліктер және оларға амалдар қолдану Құрамында сандар, айнымалдар, сандар мен айнымалдардың натурал дәрежесі және олардың көбейтіндісі болатын өрнек бірмүшелік деп аталады.
Мысалы
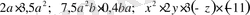 өрнектері бірмүшеліктер.
өрнектері бірмүшеліктер.
Кез-келген өрнекті қалыпты түрге, яғни бірінші орында жалғыз сандық көбейткіш (коэффициент), ал бірдей айнымалдардың көбейтіндісін дәреже түрінде көрсетілген түрге келтіруге болады. Мұндағы, барлық айнымалдардың дәреже көрсеткіштерінің қосындысы бірмүшеліктің дәрежесі деп аталады.
Екі бірмүшелік берілсін. Егер олардың арасында көбейту белгісін қойсақ, онда бастапқы бірмүшеліктердің көбейтіндісі деп аталатын бірмүшелік алынады. Бірмүшелікті натурал дәрежеге шығарса да бірмүшелік алынады. Әдетте, нәтижені қалыпты түрге келтіреді.
Қалыпты түрге келтірілген бірмүшеліктер бірдей немесе олардың тек қана коэффициенттері ғана әртүрлі болса, олар ұқсас бірмүшеліктер деп аталады.
Ұқсас бірмүшеліктерді қосуға және азайтуға болады, нәтижесінде бастапқыға ұқсас бірмүшелік алынады. Ұқсас бірмүшеліктерді қосу және азайту ұқсас мүшелерді келтіру деп аталады.
Мысалдар
1)
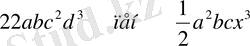 бірмүшеліктерін көбейту керек.
бірмүшеліктерін көбейту керек.
Шешуі
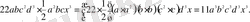
2)
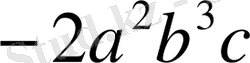 бірмүшелігін төртінші дәрежеге шығару керек.
бірмүшелігін төртінші дәрежеге шығару керек.
Шешуі
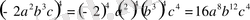
3)
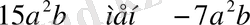 бірмүшеліктерін қосу керек.
бірмүшеліктерін қосу керек.
Шешуі
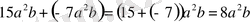
Көпмүшеліктер. Оларды қалыпты түрге келтіру Бірмүшеліктердің қосындысын көпмүшелік деп атайды. Егер көпмүшеліктің барлық мүшелерін қалыпты түрге келтіріп, ұқсас мүшелерін келтірсе, онда көпмүшеліктің қалыпты түрі алынады.
Кез келген бүтін өрнекті көпмүшеліктің қалыпты түріне келтіруге болады. Бүтін өрнекті теңбе-тең түрлендірудің негізгі мақсаты да оларды көпмүшеліктің қалыпты түріне (немесе бірмүшелікке) келтіру.
Мысал Келесі бүтін өрнектерді ықшамдау керек (яғни, көпмүшеліктің немесе бірмүшеліктің қалыпты түріне келтіру керек) :
1)
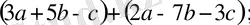
2)
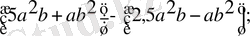
3)
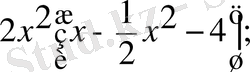
4)
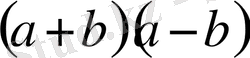 ;
;
5)
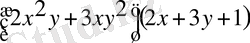
Шешуі
1) Егер жақша алдында плюс таңбасы тұрса, онда жақша ішіндегі қосылғыштардың таңбаларын сақтап, жақшаны алып тастауға болады:
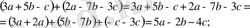
2) егер жақша алдында минус таңбасы тұрса, онда жақша ішіндегі қосылғыштардың таңбаларын қарама-қарсы таңбаларға өзгертіп, жақшаны алып тастауға болады:
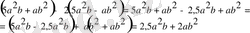
3) Үлестірімділік заңға сәйкес бірмүшелік пен көпмүшеліктің көбейтіндісі, осы бірмүшелік пен көпмүшеліктің әрбір мүшелерінің көбейтінділерінің қосындыларына тең:
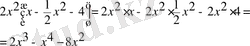
4) Екі көпмүшеліктің көбейтіндісі бірінші көпмүшеліктің әрбір мүшесін екінші көпмүшеліктің әрбір мүшесіне көбейтіп қосқанға тең:
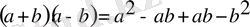
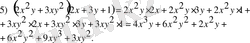 Equation. 3
Equation. 3
Енді алынған мүшелердің ұқсас мүшелерін келтіреміз:
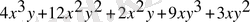
Қысқаша көбейту формулалары Кейбір жағдайларда бүтін өрнекті қалыпты түрге келтіру қысқаша көбейту формулалары деп аталатын тепе-теңдіктерді пайдаланумен іске асады. Осы тепе-теңдіктерді келтірейік:
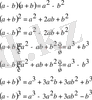
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz