Сызықтық алгебралық теңдеулер жүйесін шешудің итерациялық және вариациялық типтегі әдістері


МАЗМҰНЫ
КІРІСПЕ . . .
1. 3 Сызықтық алгебралық теңдеулер жүйесін
шешудің итерация әдісі . . .
1. 4 Сызықтық алгебралық теңдеулер жүйесін
Зейдель әдісімен шешу . . .
2. 6 Қателік минимизациясы . . .
ҚОРЫТЫНДЫ . . .
33
36
ҚОСЫМША . . . 39
КІРІСПЕ
Батыс Эвропаның ұлы ойшылы Бэкон Роджердің «Математика табиғат философиясының - әліппесі » деп барлық ғылымның мәнін математикаға негіздеген. Қазіргі ғылымның бәрі математикамен тығыз байланысты.
Қазіргі қоғамның дамуы жоғарғы техникалық дәрежемен, өнеркәсіп құрылымын ұйымдастыруының күрделіленуімен, шаруашылық басқарма және жоспарлау әдістеріне қойылатын жоғарғы талаптармен сипатталады. Математика мен қазіргі есептеу техникасының кейінгі жетістіктері экономикалық жоспарлау мен зерттеулерде кең өріс алып отыр. Қазіргі уақытта, күрделі экономикалық жүйелерді зерттеу әдістері мен математикалық модельдерді игеруге арналған, қолданбалы математиканың жаңа саласы кең ауқым алып отыр. Бұл өнеркәсіптің кең етек жайуына, Жер ресурстарының шектеулі екенін сезінуіне, энергияны, материалдарды, жұмыс уақытын тиімді қолдануына, экономика, экология және техникалық жаратылыстану ғылымдарының әртүрлі процестерін рационалды басқаруына негізделеді. Қазіргі заманға дейін біртіндеп дамып үлкен жетістіктерге жетіп отыр. Міне осы заманға дейін ақпараттық технология қарқын дамып келеді.
XXI ғасыр - жаңа технология мен ақпараттандыру ғасыры. Елбасымыз Қазақстан халқына жолдауында да қазіргі заманғы инфарақұрылымды әрі қарай дамыту мақсаты көзделген.
Адамның барлық іс-әрекет саласында жуықтау есептерді шешу математикалық программалаудың негізін құрайды. Математикалық программалаудың құрама бөліктері болып сызықтық, сызықтық емес және динамикалық программалау табылады.
Практикада сызықтық программалаудың есептері жетік меңгеріліп, шешімнің алгоритмдері тұрғызылған.
Қай сала болсын өзінің даму тарихына шолу, мен үшін бір парыз деп білемін. Математика анау Мысыр, Вавилоннан бастау алып бірнеше ғалымдардың адамзат мәдениетінің қалаптасуы мен даму процесінде атқарған ролдері өте зор. Қытай халқынан қалған тамаша ескерткіш «Тоғыз тараулы математика немесе тоғыз кітаптағы математика» («Цзю чжан суань шу») деп аталатын еңбектің сегізінші кітабы «Фанчен» алгебралық сызықтық теңдеулер жүйесіне келтірілген. «Фанчэн» деген сөз алгебралық теңдеулер жүйесін шешу алгоритмі дегенді білдіреді. Және де бұл кітапта матрицалар теоремасының элементтері баяндалған, бұл үлкен жетістік. Сызықтық алгебралық теңдеулерді есептеу тақтасының көмегімен шешулері табылған. Есептеу тақтасын сол заманғы есептеу машинасы ретінде қараған.
Дипломдық жұмыс, Сызықтық алгебралық теңдеулер жүйесін шешу әдістері деп аталатын, сызықтық алгабралық теңдеулердегі және вариациялық типтегі итерациялық есептерін шешудегі әдістерді зерттеуге арналған. Вариациялық типтегі әдістері жуықтау және минимизация есептерін шешуде қарапайым және кеңінен қолданылатын әдістерінің бірі болып табылады. Әдістің негізгі идеясы
Сызықтық алгебралық теңдеулер жүйесін
Ax=b (1)
түріндегі матрица ретінде қарастырып, бұл жүйенің бірінші теңдеуін x 1 -ге, екіншісін x 2 -ге қатысты шешеді. Ол (1) жүйесіне эквивалентті деп аталып былай белгіленеді:
(2)
Мұнда
 -матрица,
-матрица,
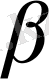 -вектор ретінде қарастырылады. (2) жүйені тізбектеп жуықтау әдісімен шешеді.
-вектор ретінде қарастырылады. (2) жүйені тізбектеп жуықтау әдісімен шешеді.
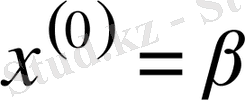 - нөлдік жуықтау ретіндегі босмүшелер бағаны. Онда кез-келген
(k+1)
-ші жуықтауы:
- нөлдік жуықтау ретіндегі босмүшелер бағаны. Онда кез-келген
(k+1)
-ші жуықтауы:
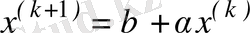
. (3)
түрінде жазылады.
(3) формуласымен анықталатын тізбектеп жуықтау әдісі итерация әдісі болып табылады.
Зейдель әдісі итерациялық әдісінің модификациясы. Итерацияның Зейдель әдісі сандар қадамы қарапайым итерациядан көрі көбірек дәл нәтиже береді. Жинақталу шартында қарапайым итерация процесі мен әртүрлі процесс берілген жүйе үшін жинақсыз болуы мүмкін, егер басқасы жинақталатын болса.
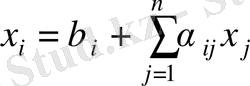
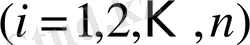 теңдеулер жүйесінен бастап
(k+1)
-ші жуықтауын құрамыз. Есеп барысында X=A'X+B түрге келтіріміз.
теңдеулер жүйесінен бастап
(k+1)
-ші жуықтауын құрамыз. Есеп барысында X=A'X+B түрге келтіріміз.
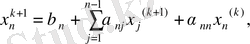 түріне келтіреміз.
түріне келтіреміз.
Вариациялық типтегі итерациялық әдістерге минималь ауытқу әдісі, жылдам түсу әдісі, минималь түзету әдісі, түйіндестік градиент әдісі, қателік минимизациясы жатады.
Оң анықталған симметриялы матрицаны қарастырады.
Ауытқуды
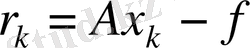 арқылы белгілейді.
Ax=f
теңдігін есепке ала отырып
арқылы белгілейді.
Ax=f
теңдігін есепке ала отырып
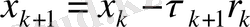
түріне жазамыз.
Минималь ауытқу әдісінде алгоритмі былай құрылады:
1.
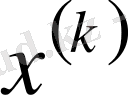 арқылы
арқылы
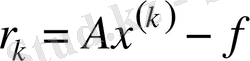 ауытқу векторы есептеледі;
ауытқу векторы есептеледі;
2.
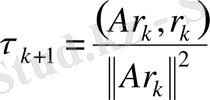 формуласы арқылы
формуласы арқылы
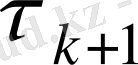 параметрі табылады.
параметрі табылады.
3.
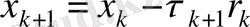 формуласынан х
к+1
векторы есептеледі;
формуласынан х
к+1
векторы есептеледі;
4. Егер
 дәлдігі берілсе, онда
дәлдігі берілсе, онда
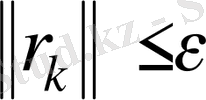 процесі тоқтайды.
процесі тоқтайды.
Минималь түзету әдісін жүзеге асыру үшін әрбір итерациялық
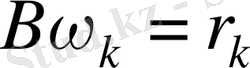 теңдеулер жүйесін шешуді талап етеді.
теңдеулер жүйесін шешуді талап етеді.
Жылдам түсу әдісі жылдамдықпен жинақталуымен және қарапайым итерация әдісі
 тиімді параметрімен дәлелденеді. Жылдам түсу әдісінің алгоримі минималь ауытқу әдісінің алгоритміне ұқсас. Тек
тиімді параметрімен дәлелденеді. Жылдам түсу әдісінің алгоримі минималь ауытқу әдісінің алгоритміне ұқсас. Тек
 параметрі мына формуламен
параметрі мына формуламен
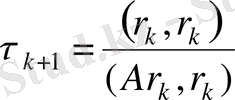 есептеледі.
есептеледі.
Түйіндестік градиент әдісі қос қадамды итерация әдісі болып табылады.
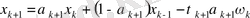
формуласымен өрнектеледі.
Қателік минимизацияның
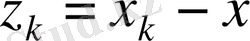 қателігі үшін
қателігі үшін
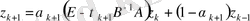 .
.
теңдеуін аламыз. Әрбір
n
үшін көбірек
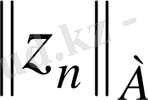 минимизациялауы талап етіледі.
минимизациялауы талап етіледі.
Дипломдық жұмыстың мақсаты сызықтық теңдеулер жүйесін шешу әдістерін зерттеу, нақты есептерді шешуде вариациялық типтегі итерация әдістерін қолдану болып табылады. Есептерді Excel кестелік процессоры көмегімен шешу.
Дипломдық жұмыс кіріспеден, екі бөлімнен, қорытындыдан, қолданылған әдебиеттер тізімінен және қосымшадан тұрады.
Бірінші тарауда сызықтық алгебралық теңдеулер жүйесін шешу әдістері қарастырылған. Бірінші тарау бес параграфтан тұрады.
Бірінші параграфта сызықтық алгебрадағы векторлар мен матрицалардың нормаларының анықтамалары және түрлері берілген. Сызықтық алгебрада норманың үш түрі: кубтық, октаэдрлік, сфералық түрі қарастырылады. Екінші параграфта сызықтық алгебралық теңдеулер жүйесі туралы айтылады. Векторлар мен матрицалардың абсолюттік және салыстырмалы қателіктері көрсетіледі. Сонымен қатар, берілген қателер бойынша шешімнің қателігін бағалау түрі туралы теорема берілген. Үшінші параграфта сызықтық алгебралық теңдеулер жүйесі үшін жалпы итерация әдісі қарастырылады. Тізбектеп жуықтау әдісімен шешу жолы, итерация процесінің жинақталуының қажеттілік шартына арналған теорема, одан туатын салдар көрсетілген. Төртінші параграфта сызықтық алгебралық теңдеулер жүйесін Зейдель әдісі арқылы шешу, (k+1) жуықтауы құрылады. Сонымен қоса, Зейдель әдісімен шешуге мысалы мен есептеу алгоритмінің кестелері қарастырылған. Бесінші параграфта қалыпты жүйе анықтамасы мен қалыпты күйге келтіру теоремалары көрсетіледі.
Екінші тарауда вариациялық типтегі итерация әдісі қарастырылады. Екінші тарау алты бөлімнен тұрады.
Бірінші параграфта вариациялық типтегі итерация әдіске қысқаша мағлұмат беріледі. Екінші параграфта минималь ауытқу әдісінің идеясы баяндалады. Бұл параграфта минималь ауытқу әдісінің теорема, анықтама, ескертуі мен мысалы келтіріледі. Және де минималь ауытқу әдісінің алгоритмі, жинақталу шарттары жазылған. Ескертуде теореманы қолданылатын пайдалы теңсіздігін қарастырып, пайдалы теңсіздікті керісінше дәлелдесе, теореманы бекітіп алатыны туралы аталған. Үшінші параграфта минималь түзету әдісі айқын емес итерациялық әдісі келтірілген
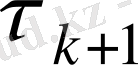 параметрі үшін өрнегі табылады. Төртінші параграфта жылдам түсу әдісі қарастырылады. Жинақталу шартымен алгоритмі, мысалымен көрсетіледі. Бесінші параграфта түйіндестік градиент әдісін қос қадамды итерация ретінде қарастырады. Бұл әдісте жуықтаулар итерацияның соңғы санына дейін жинақталатыны айтылады. Алтыншы параграфта қателік минимизациясында минимизациялаушы шарттары табылатын формулалардан құралады. Әрбір мысал Excel кестелік процессорында орындалған есептерімен толықтырылады.
параметрі үшін өрнегі табылады. Төртінші параграфта жылдам түсу әдісі қарастырылады. Жинақталу шартымен алгоритмі, мысалымен көрсетіледі. Бесінші параграфта түйіндестік градиент әдісін қос қадамды итерация ретінде қарастырады. Бұл әдісте жуықтаулар итерацияның соңғы санына дейін жинақталатыны айтылады. Алтыншы параграфта қателік минимизациясында минимизациялаушы шарттары табылатын формулалардан құралады. Әрбір мысал Excel кестелік процессорында орындалған есептерімен толықтырылады.
Қортындысында қарастырылған әдістерге талдау жүргізіліп, сызықтық теңдеулер жүйесін шешудің жалпы итерация әдістерін Зейдель әдісімен салыстыра қарастырылады. Вариациялық типтегі итерация әдістері Зейдель әдісіне қарағанда көбірек жеңіл.
Әдебиеттер тізімі дипломдық жұмысты орындауға пайдаланылған жұмыстардан тұрады.
Қосымшада 1 есепті итерацияның екі әдісімен қарастырып, Зейдель әдісімен салыстыру үш мысалдары қарастырылып, Excel кестелік процессорында орындалуы көрсетіледі.
I ТАРАУ . Сызықтық алгебралық теңдеулер жүйесін
шешу әдістері
Теңдеулер жүйесін шешу жолдары әдетте, дәл және итерациялық әдістер болып екі топқа бөлінеді. Қарастырылатын итерация әдісін қолданғанда тек жинақтылығы ғана емес жинақталу жылдамдығы да қарастырылады. Себебі, итерациялық әдіс, теңдеулер жүйесінің матрицасының түріне қарай, тез немесе өте жәй жинақталуы мүмкін, ал кей жағдайда жинақталмауы мүмкін. Сондықтан итерация әдісі жинақталатындай, эквивалентті теңдеулер жүйесімен алмастырады.
1. 1 Векторлар мен матрицалардың нормалары.
Анықтама. Х векторының нормасы-X деп мына шарттарды қанағаттандыратын теріс емес санды айтамыз:
1)
X >0
егер
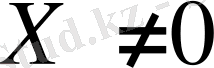 болса және
X=0
егер
Х=0
болса;
болса және
X=0
егер
Х=0
болса;
2) cX=c X, с -кез-келген сан;
3) X+У < X+У (үшбұрыш теңсіздігі) .
Соңғы екі шарттан мына теңсіздікті алуға болады
X-У > X-У .
Шынында да X =X+У-У < X-У+У.
Осыдан X - У <X-У .
Сызықтық алгебрада вектордың төмендегі үш нормасы жиі қолданылады:
1)
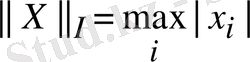 (кубтық норма) ;
(кубтық норма) ;
2)
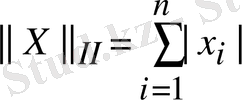 , (октаэдрлік норма) ;
, (октаэдрлік норма) ;
3)
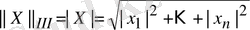 (сфералық норма) ;
(сфералық норма) ;
Анықтама.
Берілген А квадрат матрицаның нормасы-
 деп теріс емес және келесі төрт шартты қанағаттандыратын санды айтамыз:
деп теріс емес және келесі төрт шартты қанағаттандыратын санды айтамыз:
1)
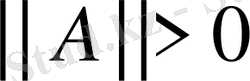 егер
егер
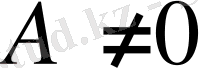 және
және
 ,
,
2)
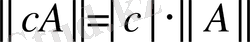 ,
,
3)
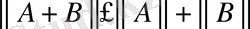 ,
,
4)
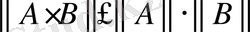 .
.
Матрицаның нормасын әртүрлі жолдармен алуға болады.
Анықтама
.
Егер А матрицасы мен Х векторы үшін
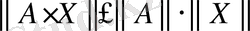 шарты орындалса, онда А матрицасы мен Х векторының нормалары келісілген дейміз.
шарты орындалса, онда А матрицасы мен Х векторының нормалары келісілген дейміз.
Матрицаның М(А) нормасы вектордың кубтық, октаэдрлік, сфералық нормаларымен келісілген, ал N(A) тек сфералық нормамен келісілген.
Шынында да, егер Х=(x 1 , x 2 , …, x n ) ' болса, онда
1.
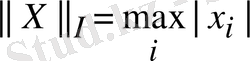 , онда
, онда
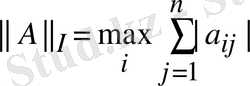 ,
,
2.
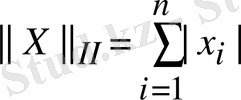 , онда
, онда
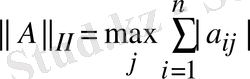 ,
,
Ақырында
3.
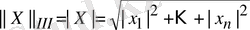 , онда
, онда
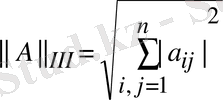 .
.
теңсіздігінен М(А) мен N(A) нормаларының вектордың сфералық нормасымен келісілгенін көреміз.
Пайдаланылған әдебиетттер
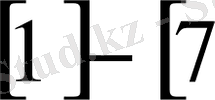
1. 2 Сызықтық алгебралық теңдеулер жүйесі (САТЖ) .
Матрицалық түрде берілген сызықтық алгебралық теңдеулер жүйесі берілсін
, (*)
Жүйенің A матрицасы берілсін, жүйе ерекше емес болсын. Бұл жағдайда жүйенің шешімі табылатыны белгілі. Вектордың абсолюттік және салыстырмалы қателігін енгізейік:
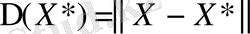 ,
,
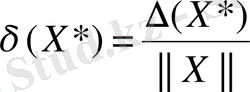 ,
,
мұндағы
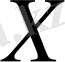 - (*) жүйесінің шешімі,
- (*) жүйесінің шешімі,
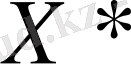 - жүйесінің шешімі
- жүйесінің шешімі
 .
.
Ал матрицаның абсолюттік және салыстырмалы қателігі:
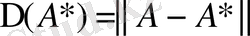 ,
,
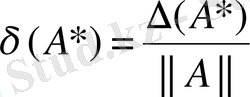 ,
,
формуламен беріледі.
Теорема
(Берілген қателер бойынша шешімнің қателігін
бағалау түрі)
.
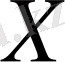 - жүйесінің шешімі
- жүйесінің шешімі
 болсын, ал
болсын, ал
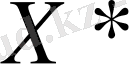 жүйесінің шешімі
жүйесінің шешімі
 , онда
, онда
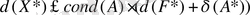 ,
,
мұндағы
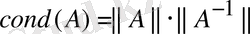 -(*) жүйесінің
шарттылығының салыстырмалы
саны.
-(*) жүйесінің
шарттылығының салыстырмалы
саны.
Бұл шарттылық саны 10-нан үлкен болса, онда жүйе нашар шарттылыланған, себебі нәтиженің қателігінің күрт арту қаупі бар.
Пайдаланылған әдебиетттер
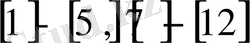
- Сызықтық алгебралық теңдеулер жүйесін
шешудің итерация әдісі.
Сызықтық теңдеуінің айнымалылар саны көп болғанда тура жауап беретін Гаусс әдісін қолдану тиімсіз. Мұндайда жуық есептеу әдістерін қолданады. Соның бірі - итерация әдісі. Итерация әдісі тізбектік жуықтау мәнін алуға мүмкіндік береді. Есептеу жағынан жүйенің дәл шешіміне жинақталады. Итерация әдісін қолданғанда көбірек тиімді болады, яғни мұндағы есептеу аралығы едәуір аз дәлдікпен талап етіледі. Сонымен қатар, итерация әдісі есептеу аралығындағы есеп қажеттіліктері біршама тұрақты. Жеке есеп қателіктері итерацияның алдыңғы қадамдарында келесі есептеудің келесі қажеттілігіне әсер етпейді. Енді сызықтық алгебралық теңдеулер жүйесін шешудің итерация әдісін қарастырайық.
Матицалық түрде берілген
, (1. 1)
сызықтық алгебралық теңдеулер жүйесі берілсін,
мұндағы
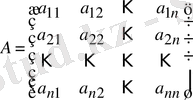 - (1. 1) жүйенің коэффицентірінің матрицасы,
- (1. 1) жүйенің коэффицентірінің матрицасы,
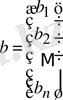 - оның бос мүшесінің бағаны,
- оның бос мүшесінің бағаны,
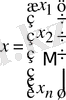 - белгісіздер бағаны.
- белгісіздер бағаны.
Диагональдық коэффициенттер
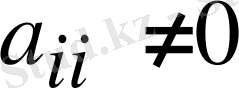
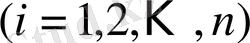 деп алып, (1. 1) жүйенің бірінші теңдеуін
деп алып, (1. 1) жүйенің бірінші теңдеуін
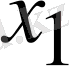 , -ге, екіншісін
, -ге, екіншісін
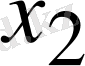 -ге т. с. с қатысты шешейік. Онда (1. 1) -ге эквивалентті
-ге т. с. с қатысты шешейік. Онда (1. 1) -ге эквивалентті
, (1. 2)
жүйесін аламыз. Мұндағы
 - элементі
- элементі
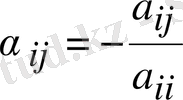 ,
,
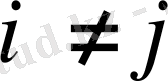 және
және
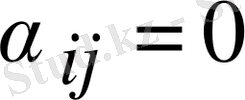 болатын
болатын

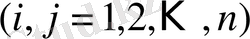 матрица;
матрица;
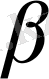 - координаталары
- координаталары
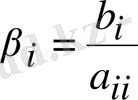
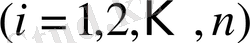 болатын векторлар.
болатын векторлар.
(1. 2) жүйесін
тізбектеп жуықтау әдісімен
шешеміз. Нөлдік жуықтау ретінде
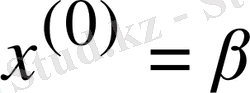 босмүшелер бағанын алайық. Онда кез-келген
(k+
1
) -
ші жуықтау
босмүшелер бағанын алайық. Онда кез-келген
(k+
1
) -
ші жуықтау
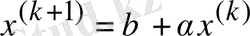
. (1. 3)
түрінде жазылады.
Егер
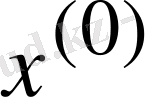 ,
,
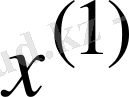 , …,
, …,
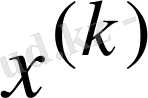 , … жуықтаулар жүйесінің
, … жуықтаулар жүйесінің
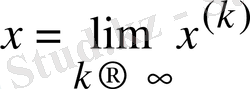 шегі бар болса, ол (1. 2) жүйенің шешімі болады.
шегі бар болса, ол (1. 2) жүйенің шешімі болады.
(1. 3) формуласымен анықталатын тізбектеп жуықтау әдісі итерация әдісі деп аталады.
Итерация процесінің жинақталуының қажеттілік шартын келтірейік.
Теорема.
Егер келтірілген (1. 2) жүйесі үшін қандайда бір
 матрицасының мөлшері 1-ден кіші болса, яғни
матрицасының мөлшері 1-ден кіші болса, яғни
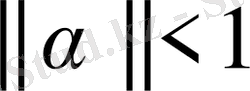 , онда итерация процесі (1. 3) бастапқы жуықтауды таңдап алудан тәуелсіз, жүйенің жалғыз шешіміне жинақталады.
, онда итерация процесі (1. 3) бастапқы жуықтауды таңдап алудан тәуелсіз, жүйенің жалғыз шешіміне жинақталады.
Салдар.
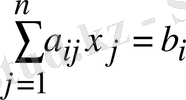
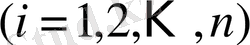 жүйесі үшін итерация әдісі жинақталады, егер
жүйесі үшін итерация әдісі жинақталады, егер
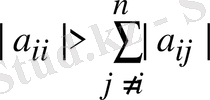
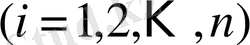 , теңсіздігі орындалса, яғни диагональ коэффициентінің модулі жүйенің әр теңдеулер үшін барлық басқа коэффициентінің модульдерінің қосындысынан артық болады. Жинақтылық теоремасы (1. 1) жүйенің коэффициентін қатал шектейді. Бірақ
, теңсіздігі орындалса, яғни диагональ коэффициентінің модулі жүйенің әр теңдеулер үшін барлық басқа коэффициентінің модульдерінің қосындысынан артық болады. Жинақтылық теоремасы (1. 1) жүйенің коэффициентін қатал шектейді. Бірақ
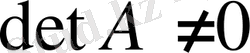 , болса жүйе теңдеуін сызықтық комбинациялау көмегімен (1. 2) жүйесіне ауыстыруға болады.
, болса жүйе теңдеуін сызықтық комбинациялау көмегімен (1. 2) жүйесіне ауыстыруға болады.
Пайдаланылған әдебиетттер
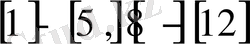
1. 4. Сызықтық алгебралық теңдеулер жүйесін
Зейдель әдісімен шешу .
Зейдель әдісі итерация әдісіне ұқсас. Итерацияның Зейдель әдісі қарапайым итерация әдісінен көрі сандар қадамы көбірек дәл нәтиже береді, ал мұндай дәлдік қадамның санына жеткен болады. Солайша келесі белгісіздер мәні мұнда көбірек дәл анықталады.
Бұл күтулер берілген ереже бойынша жүреді, демек итерацияның Зейдель әдісі жалпылай айтқанда, шынында да көбірек дәл нәтиже береді. Ол бірақ мынаны ескереді, яғни жинақталу шартында қарапайым итерация процесі және Зейдель процесі мен әртүрлі берілген жүйе үшін жинақсыз болуы мүмкін, егер олардың басқасы жинақталатын болса.
Оның негізгі идеясы,
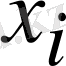 белгісізінің (
k+
1) -ші жуықтауын есептейді, алдында есептелген
белгісізінің (
k+
1) -ші жуықтауын есептейді, алдында есептелген
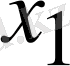 ,
,
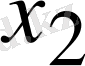 , …,
, …,
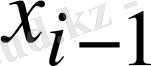 белгісіздерінен (
k+
1) жуықтаулары ескеріледі.
белгісіздерінен (
k+
1) жуықтаулары ескеріледі.
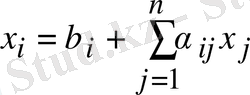
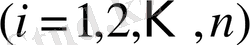
келтірілген сызықтық теңдеулер жүйесі берілсін.
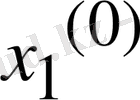 ,
,
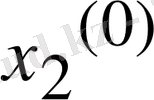 , …,
, …,
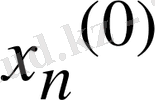 ,
,
белгісіздеріне сәйкес
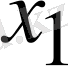 ,
,
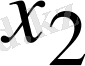 , …,
, …,
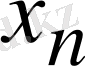
бастапқы жуықтауларды еркімізше таңдап алайық.
Одан әрі,
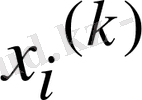 k
-шы жуықтауы белгілі деп, Зейдельге сәйкес (
k+
1) -ші жуықтауын құрамыз:
k
-шы жуықтауы белгілі деп, Зейдельге сәйкес (
k+
1) -ші жуықтауын құрамыз:
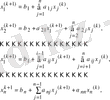
мұндағы
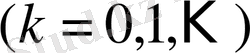 .
.
Жоғарғы жинақтылық теоремасы бойынша Зейдель әдісі үшін де дұрыс.
Зейдель әдісінің алгоритмді кесте арқылы көрсетуге болады. Бұл кесте кез-келген төрт топты жолдың әрбір санын есептей алады.
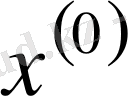
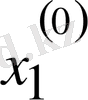
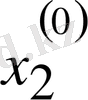
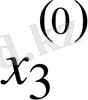



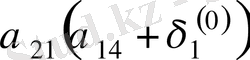
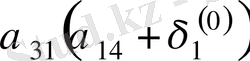
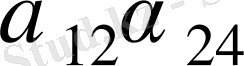
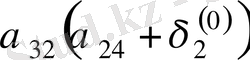
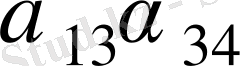
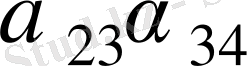
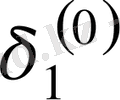
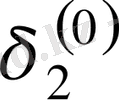
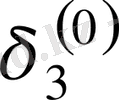
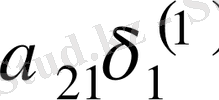
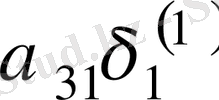
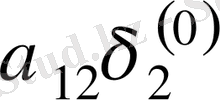
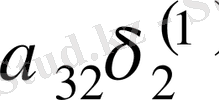
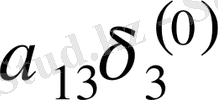
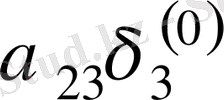
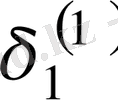
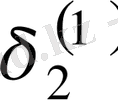
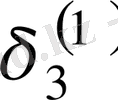
Итерацияның Зейдель әдісіне мысал қарастырайық.
1Мысал Мына теңдеулер жүйесін Зейдель әдісімен шешейік:
10x 1 + x 2 + x 3 =12
2x 1 + 10 x 2 + x 3 =13
x 1 + 2x 2 + 10x 3 =14
Бұл есепті Зейдель әдісінің алгоритміне сәйкес кесте құрайық:



Пайдаланылған әдебиетттер
1. 5. Қалыпты жүйе жағдайы.
Анықтама.
, (1. 4)
сызықты жүйені қалыпты деп атайды :
1)
А
- матрицасы симметриялы болса, онда
 ,
,
2) сәйкес квадратты форма
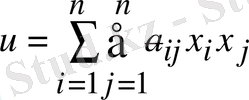 -оң анықталған болса.
-оң анықталған болса.
(1) қалыпты жүйені белгілі әдіспен
, (1. 5)
түріне келтіреміз.
Мұндағы
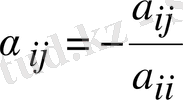 ,
,
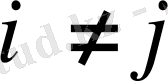 ,
,
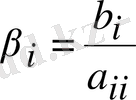 .
.
Теорема 1. Егер (1. 4) - сызықты жүйесі қалыпты болса , онда Зейдель процесі оған эквивалентті келтірілген жүйе (1. 5) үшін үнемі жинақты.
(1. 1) жүйені қалыпты түрге келтірудің бір әдісін көрсетейік .
Теорема 2.
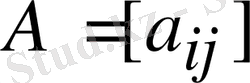 матрицасы ерекше емес
матрицасы ерекше емес
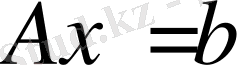 сызықтық жүйенің екі жағын
сызықтық жүйенің екі жағын
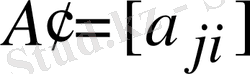 , транспорленген матрицаға көбейтсек, онда жаңа
, транспорленген матрицаға көбейтсек, онда жаңа
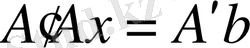 матрица қалыпты болады.
матрица қалыпты болады.
Пайдаланылған әдебиетттер
II ТАРАУ. Вариациялық типтегі итерациялық әдістер.
2. 1 Кіріспе
Өткен параграфта осындай жүйені шешудің итерация әдістерін қарастырдық.
(2. 1)
Итерациялық параметрдің шешімі үшін А матрицасының өзіне меншікті мәндері
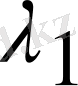 және
және
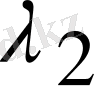 шекарасын білу керек болатын. Енді итерация әдістерінің түрін қарастырамыз.
шекарасын білу керек болатын. Енді итерация әдістерінің түрін қарастырамыз.
, (2. 2)
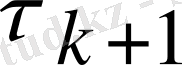 параметрі
параметрі
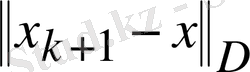 қателіктің минимум шарттарынан шығатын
қателіктің минимум шарттарынан шығатын
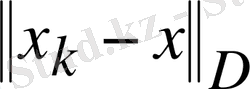 қателігі берілген. Мұнда D - берілген симметриялы оң анықталған матрицасы,
қателігі берілген. Мұнда D - берілген симметриялы оң анықталған матрицасы,
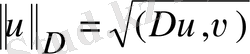 . D және В матрицаларының таңдауына байланысты әртүрлі итерацияның әдістерін аламыз. Чебышевтік итерация әдісінен, жылдамдығымен жинақталатын әдісі жоғары емес. Олардың артықшылықтары болып табылатыны, яғни А матрицасының шекарасының спекторын білуді талап етпейді. Вариациялық типтегі итерация әдістеріне минималь ауытқу әдісі, минималь түзету әдісі, жылдам түсу әдісі, қателік минимизациясы, түйіндестік градиенті жатады.
. D және В матрицаларының таңдауына байланысты әртүрлі итерацияның әдістерін аламыз. Чебышевтік итерация әдісінен, жылдамдығымен жинақталатын әдісі жоғары емес. Олардың артықшылықтары болып табылатыны, яғни А матрицасының шекарасының спекторын білуді талап етпейді. Вариациялық типтегі итерация әдістеріне минималь ауытқу әдісі, минималь түзету әдісі, жылдам түсу әдісі, қателік минимизациясы, түйіндестік градиенті жатады.
Пайдаланылған әдебиетттер
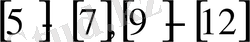
2. 2. Минимал ауытқу әдісі.
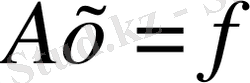 , теңдеулер жүйесінен
, теңдеулер жүйесінен
 - оң анықталған симметриялы матрица. Ауытқуды
- оң анықталған симметриялы матрица. Ауытқуды
(2. 3)
арқылы белгілейміз,
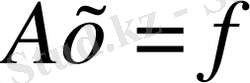 теңдеудің ауыстыруымен бірге х
k
-нің жуық мәні жақын ауытқуы болып шығады, k итерациясы (2. 1) теңдеуінен алынған. z
k
=x
k
-x қателігі және r
k
ауытқуы Az
k
=r
k
теңдігімен байланысты екенін байқаймыз.
теңдеудің ауыстыруымен бірге х
k
-нің жуық мәні жақын ауытқуы болып шығады, k итерациясы (2. 1) теңдеуінен алынған. z
k
=x
k
-x қателігі және r
k
ауытқуы Az
k
=r
k
теңдігімен байланысты екенін байқаймыз.
Айқын итерация әдісін қарастырайық
(2. 4)
және (2. 1) теңдігін еске ала отырып:
(2. 5)
түрінде жазамыз.
Минималь ауытқу әдісі
(2. 4) итерациялық әдіс деп аталады, яғни
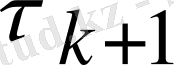 параметрі
параметрі
 берілген нормасына (к+1) -ші ауытқу нормаларынан
берілген нормасына (к+1) -ші ауытқу нормаларынан
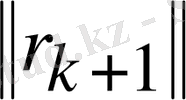 минимум шарты шығады.
минимум шарты шығады.
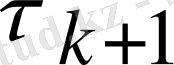 итерациялық параметрі үшін анық өрнегін аламыз. (2. 5) теңдігінен
итерациялық параметрі үшін анық өрнегін аламыз. (2. 5) теңдігінен
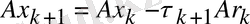
және, демек:
(2. 6)
Сонымен
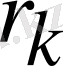 ауытқуы, z
k
=x
k
-x қателігі бұл теңдеуді қанағаттандырады.
ауытқуы, z
k
=x
k
-x қателігі бұл теңдеуді қанағаттандырады.
(2. 6) теңдеуінің бөлімінің екі бөлімі де квадратқа скаляр,
(2. 7)
теңдігін аламыз.
Бұл теңдіктен
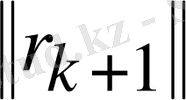 минимумына жететіні белгілі, егер
минимумына жететіні белгілі, егер
. (2. 8)
Минималь ауытқу әдісінде
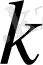 -дан (
-дан (
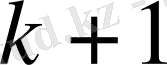 ) -ші итерациясына көшу келесі бейнемен жүзеге асады. Табылған
) -ші итерациясына көшу келесі бейнемен жүзеге асады. Табылған
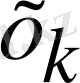 мәнімен
мәнімен
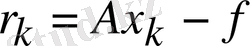 ауытқу векторы есептеледі және (2. 8) формуласында
ауытқу векторы есептеледі және (2. 8) формуласында
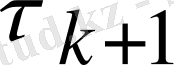 параметрі болады. Содан кейін (2. 5) формуласымен
параметрі болады. Содан кейін (2. 5) формуласымен
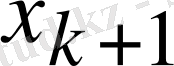 векторы шығарылады.
векторы шығарылады.
(2. 5), (2. 8) минималь ауытқу әдісі мына жылдамдықпен және де қарапайым итерация әдісі
 параметрінің үйлесімімен жинақталады.
параметрінің үйлесімімен жинақталады.
Теорема 1 . А- симметриялы оң анықталған матрица. Минималь
ауытқу әдіснің қателігі үшін бағалауы орындалады.
, n=0, 1 , …, (2. 9)
бұдан
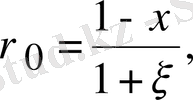
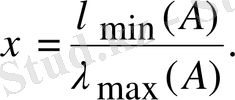 (2. 10)
(2. 10)
Дәлелдену
і
. (2. 7) тепе-теңдігін қарастырамыз. Берілген
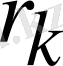 векторының оң бөлігі бұл тепе-теңдігі минимумына жетеді, егер
векторының оң бөлігі бұл тепе-теңдігі минимумына жетеді, егер
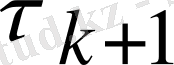 (2. 8) сәйкес таңдалса.
(2. 8) сәйкес таңдалса.
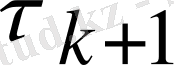 басқа мәнінде (2. 7) тепе-теңдігінің оң бөлігі тек қана үлкеюі мүмкін. Сондықтан, ойлай келе (2. 7) тепе-теңдігінен
басқа мәнінде (2. 7) тепе-теңдігінің оң бөлігі тек қана үлкеюі мүмкін. Сондықтан, ойлай келе (2. 7) тепе-теңдігінен
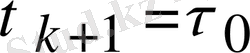 , сәйкес
, сәйкес
, (2. 11)
теңсіздігін аламыз
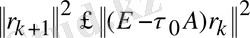
демек
(2. 12)
түрінде жазады.
§4 теоремаға сәйкес
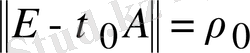 , сондықтан
, сондықтан
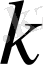 барлығында теңсіздігі дұрыс
барлығында теңсіздігі дұрыс
(2. 13)
немесе, тура солай, теңсіздік
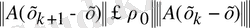
түрінде жазады. Осыдан және (2. 9) бағалануы шығады.
Ескерту . Теореманың дәлелденуін қолдана отырып, пайдалы теңсіздікті алуға болады.
(2. 14)
симметриялы оң анықталған А матрицасы және
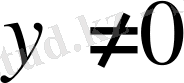 әртүрлі векторлары үшін дұрыс. (2. 14) Дәлелдеу үшін (2. 7) тепе-теңдігін
әртүрлі векторлары үшін дұрыс. (2. 14) Дәлелдеу үшін (2. 7) тепе-теңдігін
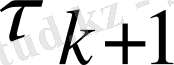 үшін жазамыз, (2. 8) сәйкес келеді. Онда мына түрге келеміз:
үшін жазамыз, (2. 8) сәйкес келеді. Онда мына түрге келеміз:
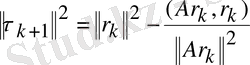
(2. 13) теңсіздігін есепке ала отырып, мынаны аламыз
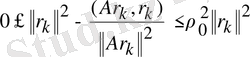
немесе
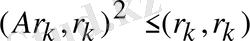
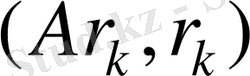 ,
,
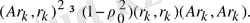
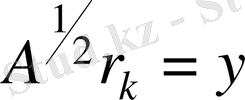 ауыстырсақ
ауыстырсақ
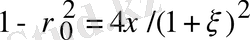 ,
,
теңсіздігімен сәйкес аламыз
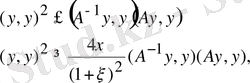
(2. 14) теңсіздігімен сәйкес келеді. Керісінше, егер (2. 14) теңсіздігін тікелей дәлелдесе, онда олардан теорема1 бекітіп алып шығуға болады.
Айталық
, (2. 15)
теңдеулер жүйесі берілсін, мұнда
 ,
,
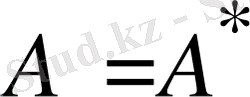 ,
,
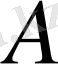 - оң анықталған эрмиттік матрица.
- оң анықталған эрмиттік матрица.
Егер
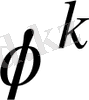 - (2. 15) жүйесінің қандай да бір жуықтауы берілсе, онда келесі
- (2. 15) жүйесінің қандай да бір жуықтауы берілсе, онда келесі
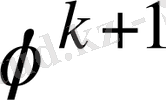 жуықтауды
жуықтауды
, (2. 16)
түрінде іздейміз. Мұнда
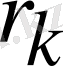 - ауытқу,
- ауытқу,
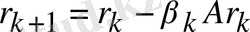 .
.
Скаляр көбейтіндісін қарастырайық:
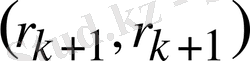
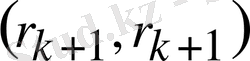 скаляр көбейтіндісі
скаляр көбейтіндісі
, (2. 17)
болғанда минималь мәнге ие болады.
(2. 16) -ны (2. 15) -ке қойсақ
, (2. 18)
түріндегі минималь ауытқу әдісін аламыз.
Енді минималь ауытқу әдісінің алгоритміне тоқталып кетейін. Минимал ауытқу әдісінде (к+1) итерациясы мынандай тәсілдермен жүзеге асады:
1)
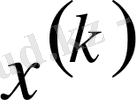 табылған мәнімен
табылған мәнімен
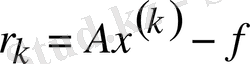 ауытқу векторы есептеледі;
ауытқу векторы есептеледі;
2) Мына формуладан
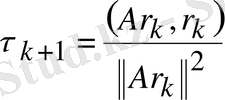
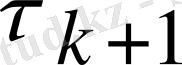 параметрі табылады. (егер
параметрі табылады. (егер
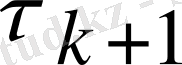 (2. 8) формуласымен анықталса,
(2. 8) формуласымен анықталса,
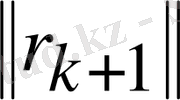 минимумына жететінін байқаймыз) . Мұнда (*, *) - скаляр туындысы;
минимумына жететінін байқаймыз) . Мұнда (*, *) - скаляр туындысы;
3)
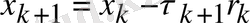 формуласынан х
к+1
векторы есептеледі;
формуласынан х
к+1
векторы есептеледі;
4) Егер
 дәлдігі берілсе, онда
дәлдігі берілсе, онда
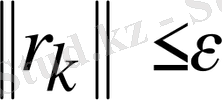 процесі тоқтайды.
процесі тоқтайды.
Бекіту
(2. 17), (2. 18) минималь ауытқу әдісі мына жылдамдықпен, яғни қарапайым итерация әдісімен орташа параметрі біріктіріледі. 0
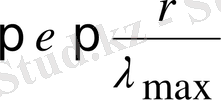 .
.
Итерацияның минималь ауытқу әдісіне мысал келтірсек:
2-Мысал
Итерацияның ауытқу әдісімен тапсырма үшін екі қадамын қарастыру:
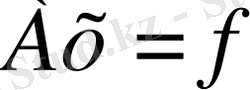 А =
А =
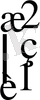 Equation. 3
Equation. 3
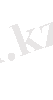
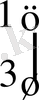 , f=
, f=
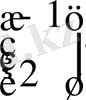 Equation. 3,
Equation. 3,
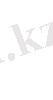 Equation. 3
Equation. 3
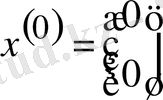
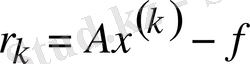
Шешуі: А - матрицасы симметриялы, А>0, сондықтан әдісті қолдануға болады.
1 қадам (к=0) 1) r 0 = Ax (0) -f: ауытқуын табайық
r
0
=
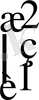 Equation. 3
Equation. 3
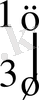 Equation. 3 *
Equation. 3 *
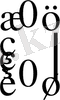 Equation. 3 -
Equation. 3 -
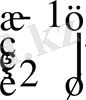 Equation. 3 =
Equation. 3 =
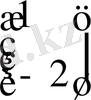 Equation. 3
Equation. 3
2) (2. 8) формуласынан итерацияның
 параметрін есептейік:
параметрін есептейік:
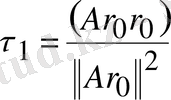 Ar
0
=
Ar
0
=
 Equation. 3
Equation. 3
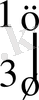 Equation. 3
Equation. 3
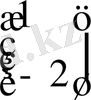 =
=
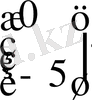 Equation. 3 ;
Equation. 3 ;
(
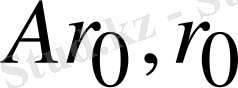 ) =(0; -5)
) =(0; -5)
 Equation. 3 *
Equation. 3 *
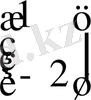 Equation. 3 =10;
Equation. 3 =10;
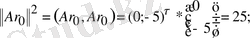
Сонда
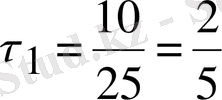
3) (2. 5) формуласымен бір жуықтауды табамыз:
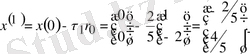
4)
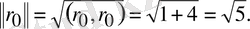
2-қадам
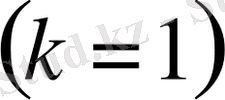
1)
Ауытқуды табамыз
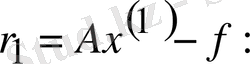
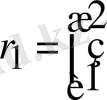
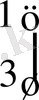
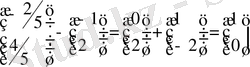
2) (2. 8) формуланы пайдаланып
 табамыз:
табамыз:
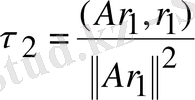
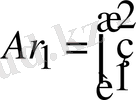
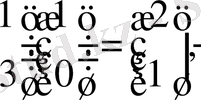
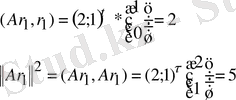
Онда
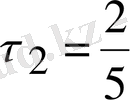
3) (2. 5) формуласынан екі жуықтауды табамыз;
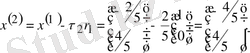
4)
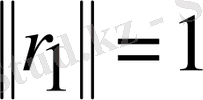
3-қадам
1)
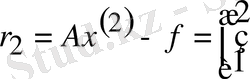
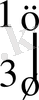
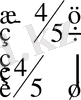 -
-
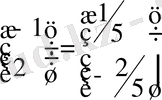
2)
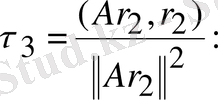
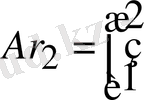
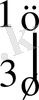
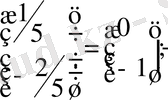
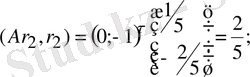
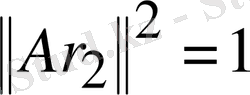
Бұдан
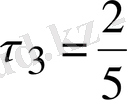 ;
;
3)
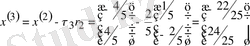
4)
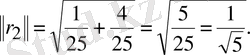
Шешімі:
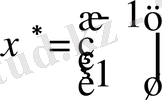 екенін байқаймыз.
екенін байқаймыз.
Пайдаланылған әдебиетттер
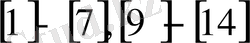
2. 3. Минималь түзету әдісі
Айқын емес итерациялық (2. 2) әдісті мына түрде жазып қоямыз
(2. 19)
мұнда
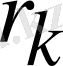 =A
x-f
- ауытқу.
=A
x-f
- ауытқу.
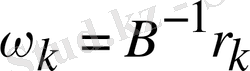 векторы (
k+1
) итерациясының түзетуі деп аталады.
векторы (
k+1
) итерациясының түзетуі деп аталады.
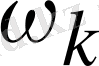 түзетуі мына теңдеуді қанағаттандырады, және де
түзетуі мына теңдеуді қанағаттандырады, және де
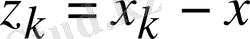 қателік айқын емес әдісі, яғни теңдеу
қателік айқын емес әдісі, яғни теңдеу
(2. 20)
В-симметриялы оң анықталаған матрица деп ұйғарайық. Минималь түзету әдісі (2. 2) айқын емес итерациялық әдіс болып табылады,
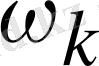 берілген векторында
берілген векторында
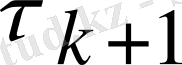 параметрі мына минимум шартының нормасынан алынады, демек
параметрі мына минимум шартының нормасынан алынады, демек
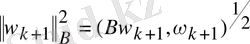 .
.
B=E болған жағдайда минималь түзету әдісі минималь ауытқу әдісіне дәл келеді.
Итерациялық
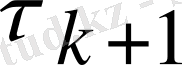 параметрі үшін өрнекті табайық. Мына түрде жазайық
параметрі үшін өрнекті табайық. Мына түрде жазайық
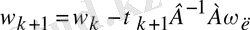
және шығарамыз
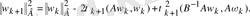
Бұдан шығатыны,
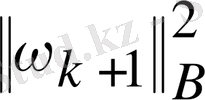 минимальды болады, егер қойсақ
минимальды болады, егер қойсақ
... жалғасы
(2. 21)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz