Стандарт емес есептерді шешудің принциптері мен әдістері және оқушылардың математикалық қабілеттерін дамыту


Мазмұны
Кіріспе . . . 3
1 Стандарт емес есептерді шешудің өзекті мәселелері мен принциптері
1. 1 Стандарт емес есептерді шығаруда оқушылардың зерттеушілік қызмет элементтерін арттыру . . . 5
1. 2 Стандарт емес есептерді шығару арқылы оқушылардың математикалық қабілеттерін дамыту . . . 9
1. 3 Стандарт емес есептерді құрастырудың кейбір мысалдары . . . 13
2 Теңдеулер мен теңсіздіктерді және олардың жүйелерін шешуде стандарт емес әдістерді пайдалану
2. 1 Алгебра курсы бойынша бағдарламадан тыс есептер . . . 17
2. 2 Математикалық логиканың элементтерін стандарт емес есептерді шығаруда қолдану (кластан тыс жұмыстар ) . . . 29
2. 3 Диофант теңдеулері . . . 33
2. 4 Теңдеулер мен теңсіздіктерді шешудің стандарт
емес тәсілдерін жоғары сыныптарда қолдану . . . 38
2. 5 Стандарт емес есептерді шешудің толық квадраттық әдісі және оны қиын есептерді шешуде қолдану мысалдары . . . 46
Қорытынды . . . 59
Пайдаланылған әдебиеттер тізімі . . . 60
Кіріспе
Қазіргі уақытта орта мектептердің негізгі міндеттерінің бірі - оқушылардың шығармашылық ойлау қабілеттерін анықтау және оларды дамыту проблемаларын шешу болып табылады.
Оқушылардың жоғары математикалық мәдениетін қалыптастырудың негізгі жолы - түрлі есептерді шығару кезінде ұйымдастыра білу.
Оқушылардың математикалық ой-өрісінің дамуы, олардың есеп шығара білуінен анық болатыны рас. Қиын да, қызықты есептерді шығара білу - оқушылардан талмас еңбекті, зор күш пен табандылықты қажет етеді. Міне, осындай қасиеттердің барлығы да оқушылардың бойында есепке деген ынтасы оянғанда ғана күшейе және арта түседі.
Демек, оқушылардың математикаға деген ойлау қабілеттерін арттыру үшін ең алдымен оқушылардың қабілеттеріне қарай қызығып шығаратын есептерді ептілікпен таңдап алуы қажет. Егер есеп, олардың қабілеттеріне сай емес, шамадан тыс қиындығы жоғары болса, онда оқушылардың есепке деген құштарлығы төмендеп, ары қарай есеп үйренуіне тежеу жасап, ынтасын қайтарады.
Кез келген жағдайда есептің шешімін болжау үшін есепке мұқият талдау жасалады. Біріншіден есепке керекті негізгі қасиетерін, фигуралардың кеңістікте орналасуын, олардың ерекшеліктерін, ұқсас белгілерін ажырата білу керек. Оқушылардың математикалық ойлау қабілетін арттырудың ең тиімді әдісі - оларды анализ және синтез, салыстыру және ұқсастыру арқылы маңызды тәсілдермен қаруландыру болып табылады. Сондай тәсілдердің бірі - стандарт (үйреншікті) есептер мен стандарт емес есептерді салыстыра отырып шешу болып табылады.
Жұмыстың бірінші тарауында стандарт емес есептерді шығарудың жалпы принциптері мен өзекті мәселелері қарастырылды. Осы тараудың бірінші және екінші параграфтерінде стандарт емес есептерді шығару арқылы оқушылардың математикалық ойлау қабілетін дамыту мәселелері қарастырылды. Ал үшінші параграфінде стандарт емес есептерді шешудің кейбір мысаладары қарастырылды.
Жұмыстың екінші тарауында теңдеулер мен теңсіздіктер және олардың жүйелерін шешудің стандарт емес әдістері қарастырылды. Осы тараудың бірінші, екінші және үшінші параграфтерінде алгебра курсы бойынша бағдарламадан тыс есептер, диофант теңдеулерін шешу және математикалық логиканың элементтерін стандарт емес есептерді шешуде қолдану( кластан тыс жұмыстарда) қарастырылды. Ал төртінші және бесінші параграфтерінде теңдеулер мен теңсіздіктерді шешудің стандарт емес тәсілдері және толық квадраттық әдісі қарастырылды.
Стандарт емес есептер оқушылардың ойлау қабілетін дамытады да, ойлауға жетелейді және есепке деген ынтасын, қызығушылығын арттырады.
Стандарт емес есептер оқушылардың есепті үйреншікті жолмен шығара салуына мүмкіндік бермейді. Демек, стандарт емес есептер оқушылардың математикалық ойлау қабілетін дамытудың негізігі құралы болып табылады.
Бұл дипломдық жұмыстың өзектілігі де осы міндеттерден келіп шығады. Математикалық білім берудегі өзекті болып есептелінетін оқушыларды бағдарламадан тыс стандартты емес есептерді шешуге үйрету мақсатындағы жұмыстар әлі де толық бір жүйеде жүргізілмей келеді. Дипломдық жұмыста ұсынылып отырған теориялық материалдар мен топтастырылған есептерді қолдану арқылы белгілі бір нәтижелерге жетуге мүмкіндік болады деп есептейміз.
1 Стандарт емес есептерді шығарудың өзекті мәселелері мен принциптері
1. 1 Стандарт емес есептерді шығаруда оқушылардың зерттеушілік қызмет элементтерін арттыру
Мектеп математика курсы оқушыларының ойлау қабілеті мен жалпы білім дәрежесін дамытуда және тәрбиелеуде әрі жетекші, әрі жауапты орын алады.
Математиканы оқытудың негізгі мақсаттары жалпы білім беру, тәрбиелік және практикалық болып бөлінеді де, олардың ішінде математиканы оқытудың жалпы білім беру мақсаты мұғалімге мынадай талаптар қоятыны белгілі: мектеп бағдарламасы анықтайтын математикалық білімнің, біліктілік пен дағдылардың барлық жүйесін оқушылардың терең және саналы меңгеруін қамтамасыз ету; математикалық тілді меңгеруге үйрету; оқушылардың нәрселер мен құбылыстардың арасындағы қатынастарды өздігінен орнату іскерлігін шыңдау; стандартты емес есептерді шығаруға, проблеммалық ахуалдарға бағдарлануды үйрету; оқушыладың нақтылы шындықты математикалық әдістермен меңгеруіне көмектесу.
Педагогикалық энциклопедияда есептің негізгі сипатамасы былайша келтірілген: оқушыда белгілі бір мақсаттың, қандай да бір сұрақтың жауабын алу үшін ұмтылушылықтың, күткен қорытындыға жетудегі табандылықтың болуы; есепті шешуге қажетті бар шарттар мен қойылған талаптарды есепке алу; осы мақсат пен шартқа сәйкес әдіс-тәсілдерді қолдану делінсе, математиканы оқытуға арналған есептерге мынадай анықтама беріледі: «Математикалық есеп дегеніміз - математикадағы заңдылықтар мен ережелер және әдіс-тәсілдер негізінде оқушылардың ой мен практикалық іс-әрекетті талап ететін және математикалық білімдерді меңгеруге, оларды практикада қолдана білуге дағдыландыруға, ойлау қабілеттерін дамытуға бағытталған ахуал» [1] .
Демек, есеп шығару математикалық ұғымдарды қалыптастырып, байытуға, оқушылардың математикалық ойлауын өрістетуге, білімдерін практикада қолдануға, табандылық, ізденгіштік, еңбек сүйгіштік қасиетерін тәрбиелуге жол ашады.
Математикалық есептерді шығара білуге үйрету және оған дағдыландыру - мұғалімдер алдында тұрған өте қиын да жауапты жұмыс. Есеп шығаруға үйрету мен дағдыландыру көбіне сыныпта өту кезінде болатындықтан, барлық оқушыларды есеп шығрудың жалпы әдіс-тәсілдерімен қаруландыру керек. Мұны іске асыру үшін олардың есеп шығару процесіндегі іс-әрекеттерін басқарып, жұмысты белгілі бір жүйемен жүргізген жөн.
Оқушылардың есепті шығара білуге үйрету процесі шығармашылық сипатта болуға тиіс. Ал шығармашылық - зерттеушілік қызметтің бір формасы, оқушылардың қабілеттерінің дамуы жайлы келелі мәселенің құрамды бөлігі болып табылады.
Мектеп математика курсында «зерттеу» сөзімен байланысты, көптен бері қалыптасқан тараулар мен есептер тобы бар. Алайда, көпшілік жағдайда, мұндағы «зерттеу» сөзінің қолданылуы формальды ғана болып, есептер шығарудағы оқушылардың қызметі зерттеушілік сипатта болмай қалады. Фактілерді тек қана жаттау арқылы, оларды терең түсініп, қолдана білу біліктілігі жоғарлауда.
Оқушылардың зертеушілік қызмет элементтерінің қалыптасуын анықтауға жүргізген тәжірибелер мен бақылау, мектеп оқушыларының көпшілігі берілген есептің «белгілі типтегі» жаттығуға жатпайтын, аз ғана ерекшеленіп, берілу тәсілі өзгертілсе, онда ондай есептерлі қалайша шығару қажеттігін, неден бастау керектігін білмейтіндігін көрсетті. Сонымен қатар зерттеушілік қызметтің негізгі элементтері болып табылатын: есепті дара есептерге бөлу, есептің аналогиясын табу, сырттай өзгеше септердің құрылымдық ұқсастығын анықтау, алынған нәтижелерді жалпылау және тағы басқа негізгі ой әркеттерін қолдана алмау фактілері жиі кездеседі. Оқушылардың көпшілігі, белгілі бір дәрежеде шығармашылықты талап ететін стандартты емес есептерді, яғни « . . . шығару алгоритмі оқушыларға белгісіз есептерді шығаруға үйретілмеген». Мысалы, квадрат теңдеулерді формула бойынша шешуге арналған есеп төменгі сыныптар үшін стандартты емес, ал « Квадрат теңдеудің түбірлерінің формулалары » тақырыбын өткен жоғарғы сынып оқушыларына ол стандартты есеп болып табылады.
Стандарт емес есептерді шығаруға қажетті зерттеушілік қызметтің негізгі екі элементін:
- есепті дара есептерге бөлу;
- сырттай әр түрлі жүйелердің құрылымдық ұқсастықтарын анықтауды жеке-жеке қарастырайық.
1. Зерттеушілік қызмет барысында зерттеуші танымның түрлі ғылыми, эмпирикалық (бақылау, эксперимент) және логикалық (аналогия, салыстыру, синтез) әдістерін қолдануы мүмкін. Алайда, математиканы оқып білуде, оның ішінде математикалық есептерді шығаруда талдаудың алатын орны зор.
Зерттеушілік қызмет процесіндегі талдаудың ғылыми зертеушілік әдіс ретінде қолдануының негізі - есептің құрамды бөліктерін ажырата білу мен есепті дара есептерге бөлу болып табылады.
Берілген А есебі дара А
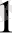 , А
, А
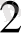 , . . . А
, . . . А
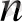 есптерге бөлінсін. Бұл дара есептердің әрқайсысы одан да майда дара есептерге бөлінуі мүмкін. Мұндай даралану зерттеушінің білімі мен тәжірибесіне байланысты өте көп немесе аз болуы мүмкін және бұл процесс зерттеуші өзіне шешімі белгілі есептер жинағын алғанда ғана тоқталады. Демек, зерттеушілік процесс барысында есепті дара есептерге бөлу зерттеу жоспарын жасау үшін қажет.
есптерге бөлінсін. Бұл дара есептердің әрқайсысы одан да майда дара есептерге бөлінуі мүмкін. Мұндай даралану зерттеушінің білімі мен тәжірибесіне байланысты өте көп немесе аз болуы мүмкін және бұл процесс зерттеуші өзіне шешімі белгілі есептер жинағын алғанда ғана тоқталады. Демек, зерттеушілік процесс барысында есепті дара есептерге бөлу зерттеу жоспарын жасау үшін қажет.
1-мысал. Ондық санау жүйесінде жазылған натурал санға төмендегі амалдар қолдануға болады:
1) соңына 4 санын қосып жазу;
2) санды 2-ге бөлу ( егер ол жұп сан болса) .
Осындай амалдарды бірнеше рет орындау арқылы 2 санынан 1976 санын алуға бола ма?
Есепті шешу үшін нені табу керек екендігін анықтап алу қажет, яғни 2 санына I немесе II амалдарын қолдану арқылы 1976 санын алу қажет. Ол үшін 1976 санының алдындағы санды білу керек. Ол санды табу оңай, себебі 1976 саны 4- ке аяқталамайды, яғни соңына 4 санын қосып жазу амалы соңғы амал емес. Онда соңғы амыл болып санды 2- ге бөлу орындалған 1976*2=3952. Енді 2-ге бөлу орындалған 1976*2=3952 . Енді А
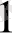 есебіне ұқсас А
есебіне ұқсас А
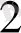 -ге көшеміз.
-ге көшеміз.
А
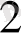 . 3952 санының алдындағы санды табу. Жоғарыдағы анықталғандағыдай, 3952 санының 7904 санын 2-ге бөлгеннен шыққандығынан табамыз да А
. 3952 санының алдындағы санды табу. Жоғарыдағы анықталғандағыдай, 3952 санының 7904 санын 2-ге бөлгеннен шыққандығынан табамыз да А
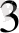 есебіне өтеміз.
есебіне өтеміз.
А
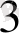 . 7904 санының алдындағы санды табу керек. Бұл процесс А
. 7904 санының алдындағы санды табу керек. Бұл процесс А
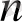 есептерінің біреуінен 2 жауабын алғанша жалғасады да, одан ізделінді операциялардың тізбегін тұрғызу ешқандай қиынға соқпайды:
есептерінің біреуінен 2 жауабын алғанша жалғасады да, одан ізделінді операциялардың тізбегін тұрғызу ешқандай қиынға соқпайды:
2 => 24 => 12 => 6 => 64 => 32 => 16 => 164 => 82 => 824 =>412 => 206 =>2064 => 1032 => 516 => 258 => 129 =>1294 =>12944 => 6472=> 3236 => 1618=>16184 =>8092 =>4046 =>40164 =>20232 =>10116 => 5058 =>50584 =>25292 => 12646 =>126464 =>63232 =>31616=>15808 =>7904 => 3952=>1976
1 - сурет
1-суреттегідей етіп бір бағананың, немесе бір қатардың, диагональдың сандарының қосындысы 18 болатындай етіп жазылған кеспелерді алған ойыншы жеңіске жетеді.
Енді 3 (ә) мысалындағы сөздерді де осындай тақтаға бір қатардағы диагоналындағы және бағандарындағы сөздердің бір ортақ әріпі болатындай етіп орналастырайық (2 - сурет) . Бұл есепте де көпшілік жағдайда бастапқы берілген есепті шығру алгоритмдерін белгілі дара есептерге бөлуге болады. Себебі есепті дара есептерге бөле білу зерттеушілік қызметке өте қажетті және оның негізгі элементі болып табылады.
2. Зерттеушілік қызметтің негізгі қасиеттерінің бірі зерттелуге қажет объектінің құрылымын көре білу, оны өзіне жақын объектімен салыстыру арқылы құрылымдық ұқсастықтарын анықтау.
2 (а) - мысал. 3 және 5 литрлік ыдыстардың көмегімен бөшкеге 22 литр суды қалай құюға болады?
2 (ә) -мысал. 22 теңгені 3 және 5 теңгелердің көмегімен қалай майдалауға болады?
Бұл екі есеп сырттай әр түрлі болғанымен метематикалық құрылымдары бірдей. Яғни 2 (а) мен 2 (ә) есептері құрылымы жағынан бірдей де, кез-келген біреуінің шешімі бізге екіншісінің шешімін береді.
Төмендегідей мысалдар қарастырайық:
3 (а) - мысал. 1 -ден 9 -ға дейінгі сандар жазылған 9 карточка берілсін. Оййыншылар кезегімен бір-бірден карточка алады. Сандарының қосындысы 15 - ке тң үш карточка алған ойыншы ұтады.
3 (ә) - мысал. «Сегіз», «ғалым», «мен», «сағым», «ғарышкер», «заман», «сан», «ойын», «ұзын» - сөздерінің әрқайсысы жеке кеспе қағаздарға жазылып, столға теріс жағымен жайылған. Ойыншылар кезегімен кеспелерді алады. Ортақ әріпі бар үш кеспені бірінші алған ойыншы жеңеді.
Бұл екі есепті зерттеу барысында - қай уақытта бірінші бастап алған ойыншы жеңеді, әлде екінші ойыншы жеңеді, болмаса тең түседі? -деген сұрақ туады. Екі есептің де қарапайым «х, 0» ойынына изоморфты екенін байқаймыз. 3(а) есебіндегі сандарды шаршылардан тұратын тақтаға диагоналы мен қатарында және бағандарындағы сандардың қосындысы 18 болатындай етіп орналастырайық.
2 - сурет
Сонымен, стандарт емес есептерді шығару барысында зерттеушілік қызметтің элементтерін пайдалану теориялық материалды есте сақтауға, практикалық есептерді шешу үшін қолдануға, өздігінен қорытынды жасауға ықпал етеді.
1. 2 Стандарт емес есептерді шығару арқылы оқушылардың математикалық қабілеттерін дамыту
Оқушылардың математикалық даму дәрежесі олардың есеп шығара білуінен анық байқалады. Есеп дегеніміздің өзі - әрбір мектеп оқушысының ақыл-ойын ұштаудың негізгі құралы. Әдеттен тыс, қызықты есептердің шешімін табу балалардың математикалық шығармашылығында маңызды орын алады. Ең әуелі, есеп шығаруды үйрену - оның шешімін табу екенін есте ұстаған жөн. Д. Пойа «Математикалық таным» кітабында (М. 1976 . 13- бет) былай деп жазды: «Егер сіз жүзуді үйренем десеңіз, тайсалмай суға сүңгіп кетіңіз, ал есеп шығаруды үйрену үшін оның шешімін табыңыз » [2] .
Кез келген қиын есепті шығару оқушыдан үлкен еңбекті, ерен күші мен табандылықты талап еседі. Бұл қасиеттер баланың есепке ынтасы оянғанда күшейе түседі. Қызықты есептер ақыл-ой энергиясын қозғалысқа келтіретіндіктен, оларды шешу оңайға түседі. Міне, сондықтан мұғалім оқушылар қызығып, өз еріктерімен шығаратын есептерді таңдап алуы қажет.
Оқушылардың математикалық қабілеттерін дамыту және математикаға ынтасын тәрбиелеуде әзіл - есептер мен матеметикалық ребустарды пайдалану тиімді. Есепті шығара алатынына оқушының сенімді болуы да табысқа жеткізетін маңызды фактордың бірі. Есеп шамадан тыс қиын болса, мектеп оқушысының шарасы таусылып, ойлау нәтижелігі төмендейді, әрі қарай үйренуіне нұқсан келеді. Мұғалім есептерді ептілікпен таңдау арқылы өз шәкірттерінің сенім күшін, жігері мен қызығуын, оның шешімін табуға ұмтылуы, қолдан келетіні сену- жетістікке жету үшін қажет алғы шарттар. Әрбір есепті шығару процесіндегі төрт сатыны ажырата білген дұрыс: 1) есептің шартын ұғу; 2) жоспарын құру; 3) жоспарды жүзеге асыру; 4) « артқа көз салу», яғни табылған шешімді пысықтап үйрену.
Оқушының меңгерген материалын шығармашылықпен ұғынуы және жаңа іс- әрекет тәсілдерінің туындап, дамуы ойлаудың мынадай үш құрамының болуына байланысты: 1) анализ және синтез, салыстыру, аналогия, классификация тәрізді қарапайым ойлау операцияларының жоғарғы деңгейде қалыптасуы; 2) көп болжам, шешімдер варианттары мен тосын идеялар ұсынудан көрінетін ойлау белсенділігінің жоғары деңгейі; 3) өзіндік ойлау әдісінен көрінетін ұйымдасқандық пен мақсаткерліктің жоғары деңгейі.
Аталған ойлау сапаларының қалыптасу оқушының шығармашылық тұлғасын дамытуға оқу материалын игерудегі қиындықтарды жеңуге жол ашады. Мұның мәні мынады, оқушы білім мен іс- әркеттің теориялық негізделген тәсілдерін қолданады немесе қойылған мәселені шешуге жаңа тәсілдерді өз бетінше таба алады. Мұғалімнің міндеті осы айтылған ойлау компоненттерін қалыптастыра білу болмақ. Ал оның кілті - шығармашылық есеп шығарту. Оқушылардың шығармашылық есептерді шығаруы олардың білім, білік, дағдысы арқылы іске асады. Сонымен қатар, сабақта жоғары белсенді ойлау әрекетінің сақталуында мотивация, оқушының өз ісіне ынтасы рөл атқарады. Демек, оқушының шығармашылық іс-әрекетке бейімдейтін, ақыл-ойын, дамытатын құрал деп қызықты есептерді («долбарлау» есептері, басқатырғылар, логикалық есептер ) айтуға болады. Оларды шығармашылық іс-әрекетті жетілдіріп, ақыл-ойды жаттықтырып көмекші, қосымша жол ретінде ұтымды пайдалану мүмкіндігі мол.
Мұндай материалдар сан алуан болғанымен, төмендегідей ортақ қасиеттері бар.
- Қызықты есептердің шешу жолы белгісіз. Олардың шешіміне жету «ойдың броундық қозғалысы» тәрізді, яғни байқап көру, қателесу әдісімен іске асады. Байқап көру арқылы іздену жеке жағдайларда негізгі шешімге бастайтын тізгінді қолға ұстатады;
- Қызықты есептер оқушының пәнге қызығуына, белсенділігіне негіз болады Есептің сюжетінің шешілу жолының әдеттен тыс болуы бала көңіліне әсер етіп, қайткенде де оны шығаруға итермелейді;
- Қызықты есептер ойлау заңдылықтарын білуге негізделіп жасалады.
Міне, осындай есеп түрлерін жүйелі түрде қолдану аталған ойлау операцияларын дамытуға, балалардың математикалық түсініктерін қалыптастыруға жағдай жасайды. Қызықты есептерді шығару көбінесе байқап көріп іздену процесімен жүреді. Ойша болжай білу балалардың бойындағы тапқырлық пен аңғарымпаздықты байқатады. Тапқырлық - шығармашылықтың ерекше көрінісі, ол талдау, салыстыру, жалпылау, байланыстарды анықтау, ұқсастыру, тұжырымдау ой елегінен өткізіп, өзара байланыстарды анықтай білу, соның негізінде есеп шығарушы бір тұжырымға келіп, ойын топтайды. Аңғарымпаздық өз білімін кәдеге асыра білудің көрсеткіші болып табылады. Қызықты есептердің шешімін болжауға қол жеткізетін тапқырлық пен аңғарымпаздық ғайыптан келер нәрсе емес. Мұндай ақыл -ой әрекетінің жетістігін оқыту процесінде дамытуға болады, әрі солай ету қажет.
Кез келген жағдайда есептің шешімін болжау үшін мұқият талдау жасалады: есептің басты қасиеттерін, фигуралардың кеңістіктегі орналасуы мен топтасуын, олардың ерекшелігін, ұқсас белгілерін ажырата алу. Алайда, қызықты есептерді шығару үшін байқау және қателесу әдісі оншалық сенімді әрі жан- жақты емес. Неғұрлым тиімді әдіс - балаларды ақыл-ой әректінің анализ және синтез, салыстыру, ұқсастыру, дәрежелеу тәрізді маңызды тәсілдермен қаруландыру.
Бірнеше есеп қарастырып көрейік.
№ 1.
АВСД дөңес төртбұрышының диагоналдары Е нүктесінде қиылысады. АВД, АСД, АЕД үщбұрыштарының аудандары тиісінше 10 см
 , 9 см
, 9 см
 , 6см
, 6см
 болғанда, АВСД төртбұрышының ауданы қандай?
болғанда, АВСД төртбұрышының ауданы қандай?
Шешуі:
С
В
Е
М
А Д
Сызбасын қағазға түсіру арқылы біз есептің мәні ВСЕ үшбұрышының ауданын табуда екенін аңғарамыз. Зер салып қарап, үшбұрыштың медианасы оны теңдей екі үшбұрышқа бөлетінін еске түсіріп, АЕД үшбұрышына ДМ медианасын жүргізсек болғаны. АМД, МЕД және ЕСД тең екенін, сондықтан олардың АМ, МЕ, ЕС табандарында ( биіктіктері бірдей болғандықтан) тең екенін көреміз. Бұдан АВМ, МВЕ және ВСЕ үшбұрыштары ауданының теңдігі шығады. Демек, ВСЕ ауданы 2 см
 . Ал тұтас төртбұрыштың ауданы 15 см
. Ал тұтас төртбұрыштың ауданы 15 см
 болады.
болады.
№ 2. Бір куб берілген. Кубтың жақтарын 1 - ден 12 - ге дейінгі сандармен нөмірлегенде оның әр төбесіне қарасты сандар қосындысы бірдей болуы керек. Бұл мүмкін болса нөмірле, мүмкін емес болса себебін түсіндір.
Оқушының әр түрлі варианттарды байқап, нәтиже шығара алмаған соң «нөмерлеу мүмкін емес» дей бостайды. Бірақ себебін түсіндіре алмайды.
Шешуі:
Кубтың әрбір жағында екі төбесі бар. Кубтың жақтарына жазылған сандар қосындысы әр төбесі бойынша тең деп, оны N санымен белгілейік. Ал төбелер саны 8 болғандықтан, әр төбедегі сандар қосындысы 8N. Бұл сан кубтың жақтарында жазылған сандар қосындысынан екі есе көп болады, яғни 2(1+2+3+. . +12) =156. Одан шығатыны N=19, 5. N бүтін сан болуы тиіс, сондықтан бұлай болуы мүмкін емес.
№ 3. ВАГОН
+
ВАГОН
СОСТАВ
Әріптерді сандармен ауыстыр. Бірдей әріптер бірдей сандарға әр түрлі әріптер әр түрлі сандарға айналсын және шешуі дұрыс шықсын.
Мұндай есептер оқушыларды ерекше қызықтырады. Олар осы жолмен есеп құрастыруға тырысады.
Шешуі:
Қосылғыштардың бес орынды, ал қосындының алты орынды жұп сан екені байқалып тұр, демек «В=» 5 немесе одан үлкен сан. Жұп болуы тиіс болғандықтан 6 немесе 8-ге тең. «С» барлық вариантта 1-ге тең. Бұдан «А» саны 0 немесе 5 болатынын болжаймыз. Белгісіз әріптер біршама айқындала түскендіктен, байқау әдісін пайдалануға болады В=6 десек, шешім дұрыс болмайды. В=8 болса, Н=9. Ойлана келе А саны тек 5 болуы мүмкін екеніне көз жеткіземіз. Толық шешімі мынандай:
85679
+
85679
171358
Қызықты есептер мектептегі оқу материалының меңгерілуін және ойлау процесінің тиімділігін анықтайды. Бұл оқу процесінде анализ, синтез, салыстыру, ұқсастыру, дәрежелеу тәрізді операцияларға басты назар аударуға негіз болады. Мұндай есептерді шығаудағы ерекше ойлау процестері шығармашылық белсенділіктің де көрінісі.
1. 3 Стандарт емес есептерді құрастырудың кейбір мысалдары
Салдар. Табандары бірдей және биіктіктері бірдей үшбұрыштардың аудандары тең шамалы (1-сурет) [3] .
С С
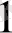 С
С
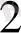 l
l
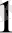 Equation. 3 ║ l
Equation. 3 ║ l
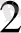 Equation. 3, АВС, АВС
Equation. 3, АВС, АВС
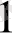 және АВС
және АВС
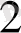
үшбұрыштарының табаны а, биіктігі h.
h
А В
1 - сурет
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz