Сызықтық емес дифференциалдық теңдеулерге арналған консервативтік ақырлы-айырымдық схемалар және вариациялық аппроксимация әдістері


Мазмұны
1 Дискретті теңдеулер
1. 1 Ақырлы - айырымдық әдістің негізі
1. 2 Аппроксимацияның негізгі әдістері. Тейлордың кесілген қатарымен берілген аппроксимация әдісі
1. 3 Айырымдық схема құрудың вариациялық принципі
1. 4. Шектік - айырымдық теңдеулер
2 Дербес туындылы теңдеулер үшін айырымдық схемалар
2. 1. Есептің қойылу сипаты
2. 2. Коэффициенттері тұрақты жылу өткізгіштік теңдеу
2. 3 Сызықтық тасымалдау теңдеуін шешудің сандық әдістері
2. 4. Консервативтік қасиет
2. 5. Ағынға қарсы өзгертілген схеманың бір түрі
2. 6. Бір өлшемді сызықтық емес теңдеулерді шешу
Қорытынды
Пайдаланған әдебиеттер тізімі
Кіріспе
Соңғы кезде есептеу математикасына байланысты көп есептер, сызықты емес есептерді шешу мәселелері қарастырылады. Математикалық физикада көп үлгілердің теңдеулері сызықты емес. Сол сызықты емес теңдеулерді үлкен дәлдікпен шешу мәселесі диссертацияда қарастырылады.
Диссертациялық жұмыстың негізгі мақсаты - Сызықтық емес теңдеулерді шешу, оған тиімді сандық әдістерді қолдану.
Біз уақыт бойынша айнымалыға және оған сәйкес дифференциялдық операторға байланыспаған айырымдық схема құруды қарастырдық. Бірақ кеңістіктік дифференциялдық оператордың аппроксимациясының түрін таңдағанда проблемалар туындайды. Аппроксимацияның бұл операторы - дифференциялдық теңдеулердегі және шеттік шарттардағы туындылар, ең қарапайым түрде шекті айырымдармен айырбасталды. Бірақ мұндай тәсіл ылғи да жетістікке әкелмейтіндігі белгілі. Барынша күрделірек, сызықтық емес теңдеулермен және коэффициенттері айнымалы теңдеулермен сипатталатын есептерде туындыларды шекті айырымдармен айырбастау, үлкен қателері болатын схемаларға әкеледі, немесе есептеуге мүлдем жарамайды. Энергияның сақталу заңына, массаға, біріңғай еркін ортаның (газдың, сұйықтың) қозғалыс санына негізделе отырып алынған дифференциялдық теңдеулерге сәйкес келетін кез келген айырымдық схемаларға қойылатын маңызды талаптарға тоқталайық.
Үзіліссіз дәл шешімдер үшін дененің кез келген облысына сақталу заңы орындалады. Айырымдық шешімдер үшін сақталу заңының орындалуын талап етудің маңызды ерекшелігі бар, ол денені дискреттік түрде бөлшектеуге бейімделген. Шынында да айырымдық шешімдер жекелеген нүктелерде ізделенетіндіктен, денені сан сондай элементарлық көлемшелерге бөлшектеу қажет, бұлардың әрқайсысында бір нүктеден бар деп ұйғарып олардан сақталу заңын еркін элементарлық көлемшелрден талап еткендей, және осы элементарлық көлемшелерден құралған кез келген облысқа да талдап қоя аламыз.
Анықтама. Энергияның сақталу заңын қанағаттандыратын (интегралдық инварианттар) сандық шешімдер алынатын айырымдық схемаларды консервативтік деп атаймыз, немесе егер айырымдық әдіс, қарастырылушы дифференциялдық теңдеулерге тиісті белгілі бір интегралдық сақталу заңын қамтамассыз ететін болса, оны консервативтік деп атаймыз.
Консервативтік қасиеттің маңыздылығын сығымдалушы ортаның үзіліс еместік теңдеуінің мысалында оңай түсінуге болады. Толықтай тұйық, қабырғалары өткізбейтін ыдыстағы кәдімгі конвекцияның есебін қарастырайық. Алғашқы уақыт сәтінде барлық тұтас көлемде V = 0 деп есептейік. Ыдыстың төменгі қабырғалырына жылу берілсін және табиғи конвекция пайда болады, мүмкін стационарлық жағдайға дейін жетеді. Егер есептеу үшін әлдеқандай консервативтік емес схема қабылданған болса, онда зерттелуші көлемдегі толық масса өзгереді. Егерде консервативтік схема қолданылатын болса, онда толық масса өзгермейді (жуықтаудың машиналық қатесін ескермеген жағдайда) . Бірінші жағдайда, массаның сақталуының бұзылғандығына орай жіберлетін қате ∆x → 0 да азаятындығын көңілге демеу етуге болады, бірақ іс жүзіндегі шекті ∆x шамасымен есептеулерде мұндай демеу әлсіз болады. Бұл түсінікті біз маңызды деп есептейміз және консервативтік схеманы қолдануды табандылықпен ұсынамыз. Бірақ бұл арада жақтайтын да қарсы болатын да жақтары барының үстіне әдебиеттерде жарияланған сандық бақылау есептеулерінің мысалдарында біржақты таңдау жасауға мүмкіндік бермейді. Осы дәлелдер мен бақылау есептеулерінің нәтижелеріне үңілейік. Консервативтік қасиет схеманың дәлдігін көтеруге міндетті түрде байланыспайды. Мысалға, консервативтік теңдеулердің орнықты шешімдері консервативтік қасиеттерді сақтайды. Оның үстіне консервативтік емес әдіс кейбір ұғымдарда консервативтікке қарағанда дәлірек болуы мүмкін. Мысалға, тордың түйіндеріндегі мәндер бойынша функцияны (анықтау) келтіру үшін жоғары ретті полиномдардың бір өлшемді аппроксимацияларын қолдануға болар еді және бұл жағдайда кеңістіктік айнымалылар бойынша туындыны анықтау жоғарырақ ретті қателерге ұрындыруы ықтимал. Бірақ бұлайша құрылған схема консервативті емес болуы мүмкін, ал егер дәлдік критериі консервативтік шартты қажет ететін болса, онда консервативтік емес схеманың дәлдігі кемдеу болады.
1 Дискретті теңдеулер
1. 1 Ақырлы - айырымдық әдістің негізі
Дифференциалдық теңдеулерді торлық әдіспен шешудің қарапайым жолы теңдеу құрамындағы туындылардың жуық өрнектерін табумен қорытындыланады.
Бұл жуық өрнектер тордың торабындағы тәуелді айнымалылар мәні және уақыт бойынша дискретті қадамдар үшін қолданумен анықталады. Бұдан олар ақырлы кеңістіктерге және уақыттың қадамға тәуелді айнымалылардың айырымы көмегімен қалыптасады. Осы себепті мұндай жақындау ақырлы - айырдық әдіс деп аталады. Қабылданған жуықтау туындылар үшін, содан кейін қарастырылып отырған теңдеулер жүйесінің дербес туындыларының аппроксимациялайтын алгебралық теңдеулер жүйесін құруда қолданылады. Бұл алгебралық жүйе тордың есептеу облысын жабатын әрбір ішкі торабында орынды деп есептейміз. Бастапқы момент және кеңістіктің шекаралық нүктелерінде есептің физикалық қойылуынан шығатын алғашқы және шекаралық шарттарды аппроксимациялайтын қосымша шарттар немесе теңдеулер анықталады. Осы түрде алынған алгебралық теңдеулер жүйесі әдетте компьютер және қандай да бір ыңғайлы көпқадамды процедура көмегімен шешіледі.
Қарапайым болу үшін бір тәуелсіз айнымалыға байланысты төмендегі (1. 1) формуласы орындалады
, (1. 1)
функциясын қарастырамыз. Сандық әдістер есептің жуық шешімін береді, яғни қандайда бір есептің
 дәл шешімінің орнына біз ізделінді функцияға қандай да бір мағынада жақындайтын басқа есептің
дәл шешімінің орнына біз ізделінді функцияға қандай да бір мағынада жақындайтын басқа есептің
 шешімін табамыз. Барлық әдістердің көрсететін негізгі мағынасы - басқа есептің қорытынды есебі дискретизациялау немесе аппроксимациялау комьютерде шығару үшін өте ыңғайлы. Аппроксимациялау есебінің шешімі қандайда бір талап етілген дәлдікпен шешімін анықтауға болатын параметрге тәуелді. Мысалы, сандық интегралдау есебіндегі мұндай параметрлер квадратуралық формуланың торабы немесе салмағы. Дискретті есептің шешімі ақырлы өлшемді кеңістіктің элементі болып табылады. Мысалға,
шешімін табамыз. Барлық әдістердің көрсететін негізгі мағынасы - басқа есептің қорытынды есебі дискретизациялау немесе аппроксимациялау комьютерде шығару үшін өте ыңғайлы. Аппроксимациялау есебінің шешімі қандайда бір талап етілген дәлдікпен шешімін анықтауға болатын параметрге тәуелді. Мысалы, сандық интегралдау есебіндегі мұндай параметрлер квадратуралық формуланың торабы немесе салмағы. Дискретті есептің шешімі ақырлы өлшемді кеңістіктің элементі болып табылады. Мысалға,
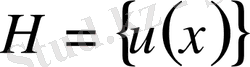 ,
,
кеңістігінің
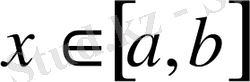 үздіксіз аргументінің
үздіксіз аргументінің
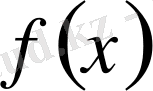 функциясының дискретизациясын қарастырайық.
функциясының дискретизациясын қарастырайық.
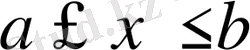 кесіндісінде тор деп аталатын
кесіндісінде тор деп аталатын
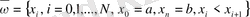 нүтелердің ақырлы нүктелер жиынын енгізейік.
нүтелердің ақырлы нүктелер жиынын енгізейік.
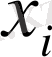 нүктесін
нүктесін
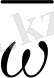 торының торабы деп атайды.
торының торабы деп атайды.
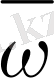 жиыны
жиыны
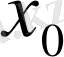 және
және
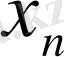 торабынсыз
торабынсыз
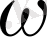 арқылы белгілейміз. Егер
арқылы белгілейміз. Егер
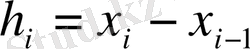 қадамы көршілес тораптардың арасындағы тұрақты (
қадамы көршілес тораптардың арасындағы тұрақты (
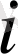 - ге тәуелді емес),
- ге тәуелді емес),
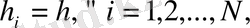 болса онда торын бірқалыпты (
болса онда торын бірқалыпты (
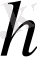 қадаммен), кері жағдайда бірқалыпты емес деп атайды. Барлық
қадаммен), кері жағдайда бірқалыпты емес деп атайды. Барлық
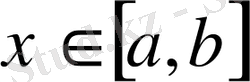 -да анықталған
-да анықталған
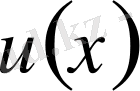 функциясының орнына
функциясының орнына
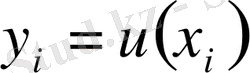 торлық функциясын қарастырамыз.
торлық функциясын қарастырамыз.
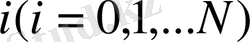 бүтінсанды аргумент немесе
бүтінсанды аргумент немесе
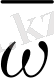 торының
торының
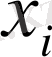 торабы, ал
торабы, ал
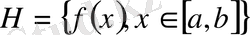 -ны (
-ны (
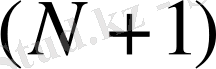 өлшемді )
өлшемді )
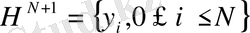 арқылы өлшемді кеңістігімен алмастырамыз.
арқылы өлшемді кеңістігімен алмастырамыз.
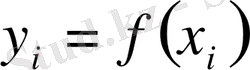 торлық функциясын
торлық функциясын
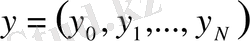 векторы ретінде қарастыруға болатындығы айқын.
векторы ретінде қарастыруға болатындығы айқын.
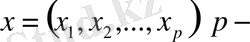 өлшемді Евклид кеңістігіндегі
өлшемді Евклид кеңістігіндегі
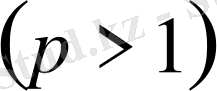 нүкте болатын
нүкте болатын
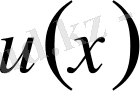 көп айнымалы функциялар кеңістігінде дискретизациялауға келтіруге болады. Сонымен,
көп айнымалы функциялар кеңістігінде дискретизациялауға келтіруге болады. Сонымен,
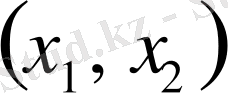 жазықтығында
жазықтығында
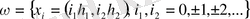 торын
торын
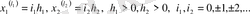 (мұндағы
(мұндағы
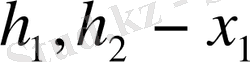 және
және
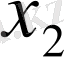 бағыты бойынша тор қадамы ) перпендикуляр түзулерінің қиылысуындағы нүктелер жиынын (торабын) сәйкесінше енгізуге болады.
бағыты бойынша тор қадамы ) перпендикуляр түзулерінің қиылысуындағы нүктелер жиынын (торабын) сәйкесінше енгізуге болады.
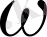 -торы әрбір жеке айнымалысы бойынша бірқалыпты екендігі айқын.
-торы әрбір жеке айнымалысы бойынша бірқалыпты екендігі айқын.
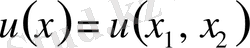 функциясының орнына
функциясының орнына
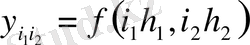 торлық функциясын қарастырайық. Егер
торлық функциясын қарастырайық. Егер
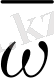 торы
торы
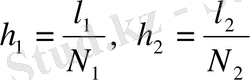 болатындай
болатындай
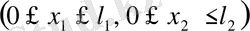 тіктөртбұрышында жататын тораптардан ғана тұрса, онда тор
тіктөртбұрышында жататын тораптардан ғана тұрса, онда тор
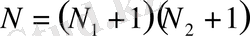 ақырлы санды тораптан тұрады, ал
ақырлы санды тораптан тұрады, ал
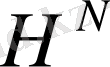 кеңістігі
кеңістігі
 торлық функциясы ақырлы өлшемді болып табылады.
торлық функциясы ақырлы өлшемді болып табылады.
Көп жағдайларда
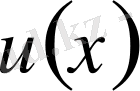 функциясын Фурье қатарына жіктелуімен берілген түрін (1. 2) формуласында қолданған ыңғайлы.
функциясын Фурье қатарына жіктелуімен берілген түрін (1. 2) формуласында қолданған ыңғайлы.
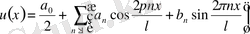 (1. 2)
(1. 2)
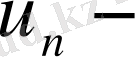 ң
ң
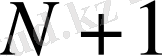 мәндері
мәндері
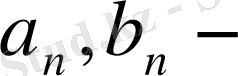 коэффициенттерінің барлығын есептеп табуға мүмкіндік бермейді немесе дәлірек айтқанда олар тек
коэффициенттерінің барлығын есептеп табуға мүмкіндік бермейді немесе дәлірек айтқанда олар тек
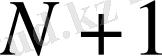 әртүрлі коэффициенттерін есептеу үшін қолданылуы мүмкін.
әртүрлі коэффициенттерін есептеу үшін қолданылуы мүмкін.
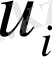 - ң
- ң
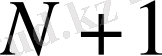 мәндері
мәндері
 мәнін анықтау үшін және қатардың ұзақтолқынды бөлігіндегі Фурье коэффициенттерінің санының максималды мүмкіндігін анықтауда қолданылады, яғни
мәнін анықтау үшін және қатардың ұзақтолқынды бөлігіндегі Фурье коэффициенттерінің санының максималды мүмкіндігін анықтауда қолданылады, яғни
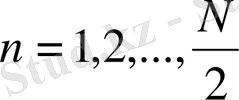 үшін коэффициенттерді. Осы компонеттердің ішіндегі ең қысқа толқын
үшін коэффициенттерді. Осы компонеттердің ішіндегі ең қысқа толқын
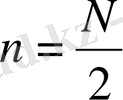 - ге сәйкес келеді, мұндағы (1. 3) формуласы толқын ұзындығын береді
- ге сәйкес келеді, мұндағы (1. 3) формуласы толқын ұзындығын береді
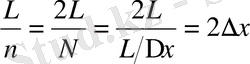 (1. 3)
(1. 3)
Осылайша таңдап,
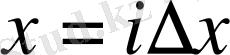 дискретті нүктелерінің
дискретті нүктелерінің
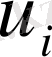 мәнінің көмегімен толқын ұзындығын
мәнінің көмегімен толқын ұзындығын
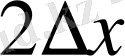 - тен кіші екенін елестету мүмкін емес деп айтуға болады. Туындылар үшін аппроксимацияны құру кезінде қолданылатын шамаларының арасындағы айырымды қарастырамыз. Бұл айырымдар ақырлы айырымдар деп аталады. Олар бір немесе бірнеше
- тен кіші екенін елестету мүмкін емес деп айтуға болады. Туындылар үшін аппроксимацияны құру кезінде қолданылатын шамаларының арасындағы айырымды қарастырамыз. Бұл айырымдар ақырлы айырымдар деп аталады. Олар бір немесе бірнеше
 интервалдарында есептелуі мүмкін. Нүктенің орналасуына байланысты туындысын анықтауды талап ететін
интервалдарында есептелуі мүмкін. Нүктенің орналасуына байланысты туындысын анықтауды талап ететін
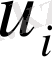 -ң алынатын мәндерінің ақырлы айырымдары центрлендірілген немесе центрлендірілмеген болып бөлінеді. Центрлендірілмеген айырымдар болып мысалы, алға (вперед) айырымы:
-ң алынатын мәндерінің ақырлы айырымдары центрлендірілген немесе центрлендірілмеген болып бөлінеді. Центрлендірілмеген айырымдар болып мысалы, алға (вперед) айырымы:
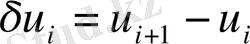
Көп жағдайда төмендегідеу центрлік айырымдар қолданылады.
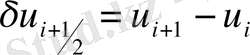
Центрлік (орталық) айырымдар, осы айырым есептелетіндей нүктеге қатысты симметриялы болатын мәндер арасындағы айырымды көрсетеді.
Дифференциалдық теңдеулерді аппроксимациялауларды құру жолдарының бірі -туындылардың ақырлы - айырымдық қатынасымен сәйкестендірілетін қарапайым алмастырумен алынады. Мәселен, бірінші ретті туынды үшін (1. 4) аппроксимацияны қолдануға болады.
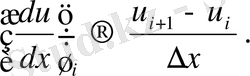 (1. 4)
(1. 4)
Бұл ақырлы - айырымдық қатынас нүктесіндегі бірінші туындыларының аппроксимацияларының мүмкін болатын мәндерінің ішіндегі бірғана ақырлысы.
Туындының ақырлы -айырымдық аппроксимациялау мағынасын жақсы түсіну үшін
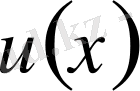 функциясының
функциясының
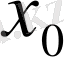 нүктесіндегі туындысын анықтауды еске түсірейік:
нүктесіндегі туындысын анықтауды еске түсірейік:
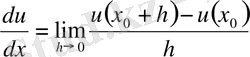 .
.
Егер
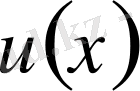 Equation. 3 функциясы үзіліссіз, ал
Equation. 3 функциясы үзіліссіз, ал
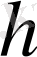 Equation. 3 - жеткілікті аз, бірақ ақырлы болса, онда айырым мәні
Equation. 3 - жеткілікті аз, бірақ ақырлы болса, онда айырым мәні
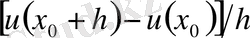 Equation. 3 айырым
Equation. 3 айырым
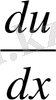 Equation. 3 туындысының мәніне өте жақындайды. Шынында да ақырлы өсімше туралы теоремадан туындының айырымдық мәні ұзындығы
Equation. 3 туындысының мәніне өте жақындайды. Шынында да ақырлы өсімше туралы теоремадан туындының айырымдық мәні ұзындығы
 интервалының қандай да бір нүктесіндегі ізделінді функцияның туындысына тең.
интервалының қандай да бір нүктесіндегі ізделінді функцияның туындысына тең.
Туындының айырымдық аппроксимациясының дәлдігін формальді түрде
 функциясын Тейлор қатарына жіктеу немесе қалдық мүшемен берілген Тейлордың формуласымен тексеруге болады.
функциясын Тейлор қатарына жіктеу немесе қалдық мүшемен берілген Тейлордың формуласымен тексеруге болады.
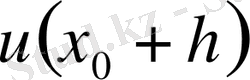 -ты
-ты
 функциясының мәні және оның нүктесіндегі туындылары арқылы өрнектейік:
функциясының мәні және оның нүктесіндегі туындылары арқылы өрнектейік:
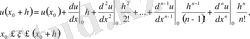
Мұндағы соңғы қосылғыш - қалдық мүше.
Алға (вперед) айырымының көмегімен өрнекті төмендегідей түрде жазамыз.
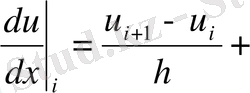 аппроксимация қателігі.
аппроксимация қателігі.
Мұндағы
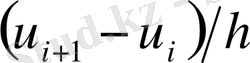 айырымы
айырымы
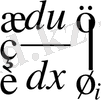 туынды түрінде берілген ақырлы айырымдық қатынас немесе қандай да бір қиынырақ өрнек туынды аппроксимация ретінде қолданылса, онда ең алдымен бұл аппроксимация келісілген болуы шарт. Демек, ол тордың қадамы 0-ге ұмтылғанда туындысына жақындауы керек. (1. 1) қатынасы осы қасиеттерге ие екені айқын.
туынды түрінде берілген ақырлы айырымдық қатынас немесе қандай да бір қиынырақ өрнек туынды аппроксимация ретінде қолданылса, онда ең алдымен бұл аппроксимация келісілген болуы шарт. Демек, ол тордың қадамы 0-ге ұмтылғанда туындысына жақындауы керек. (1. 1) қатынасы осы қасиеттерге ие екені айқын.
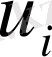 -торлық мәнінің орнына туындылар үшін жуық өрнекке
-торлық мәнінің орнына туындылар үшін жуық өрнекке
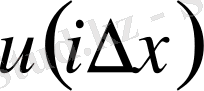 дәл шешімін қойсақ, онда кейбір пайдалы қасиеттерді алуға болады, содан кейін центрлік нүктенің аймағында
дәл шешімін қойсақ, онда кейбір пайдалы қасиеттерді алуға болады, содан кейін центрлік нүктенің аймағында
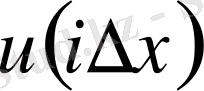 - ті Тейлор қатарына жіктелінеді.
- ті Тейлор қатарына жіктелінеді.
(1. 1) қатынасы үшін мұндай процедура төмендегідей өрнекке әкеледі.
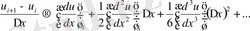
Бұл өрнектер арасындағы айырым және берілген жағдайда аппроксимациялайтын
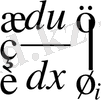 - туындысын
- туындысын
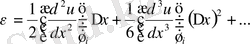 туындының аппроксимациялық қателігі деп аталады. Бұл жуықтауды қалыптастырғандағы «қию» («отсечены») болатын мүшелері. Аппроксимация қателігі
туындының аппроксимациялық қателігі деп аталады. Бұл жуықтауды қалыптастырғандағы «қию» («отсечены») болатын мүшелері. Аппроксимация қателігі
 -ң өте аз мәніндегі туындысына айымдық қатынастың жақындауының қаншалықты дәл екендігінің мәнін береді. Мұның қарапайым шамасы аппроксимация дәлдігінің реті болып табылады. Бұл аппроксимация қателігі үшін өрнектегі
-ң өте аз мәніндегі туындысына айымдық қатынастың жақындауының қаншалықты дәл екендігінің мәнін береді. Мұның қарапайым шамасы аппроксимация дәлдігінің реті болып табылады. Бұл аппроксимация қателігі үшін өрнектегі
 - ң ең кіші дәрежесі болады. Сонымен, (1. 1) аппроксимациясы аппроксимацияның бірінші ретті дәлдігі болып табылады.
- ң ең кіші дәрежесі болады. Сонымен, (1. 1) аппроксимациясы аппроксимацияның бірінші ретті дәлдігі болып табылады.
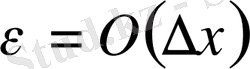 деп жазуға болады. Мұндағы,
деп жазуға болады. Мұндағы,
 - дәл математикалық мағынаны береді.
- дәл математикалық мағынаны береді.
 -түрдегі аппроксимация қателігінің көрінісі аппроксимация қателігінің
-түрдегі аппроксимация қателігінің көрінісі аппроксимация қателігінің
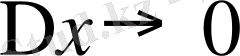 болғанда
болғанда
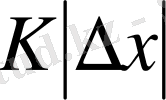 абсолютті шамасынан аспайтындығын білдіреді, мұндағы
абсолютті шамасынан аспайтындығын білдіреді, мұндағы
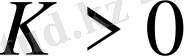 - нақты тұрақты.
- нақты тұрақты.
Бұл жағдайда аппроксимация қателігінің тәжірибелік реті
 - ке тең және жалпы теңдеудің барлық мүшелері үшін ең жоғарғы дәреже болып табылады. Жалпы жағдайда
- ке тең және жалпы теңдеудің барлық мүшелері үшін ең жоғарғы дәреже болып табылады. Жалпы жағдайда
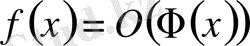 өрнегі барлық
өрнегі барлық
 үшін
үшін
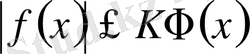 орындалатындай
орындалатындай
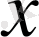 - қа тәуелсіз
- қа тәуелсіз
 бар екендігін білдіреді. Мұндағы
бар екендігін білдіреді. Мұндағы
 және
және

 -да анықталған
-да анықталған
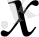 - қа тәуелді нақты функциялар.
- қа тәуелді нақты функциялар.
Аппроксимация қателігін
 түрінде көрсету қателік шамасының емес, ал оның нольге ұмтылу сипатын ғана білдіретінін атап өткен жөн.
түрінде көрсету қателік шамасының емес, ал оның нольге ұмтылу сипатын ғана білдіретінін атап өткен жөн.
1. 2 Аппроксимацияның негізгі әдістері
Тейлордың кесілген қатарымен берілген аппроксимация әдісі
Айталық,
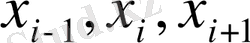 кеңістік бойынша
кеңістік бойынша
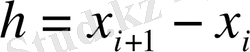 қадамымен берілген бірқалыпты айырымдық торының үш тізбектей торабы болсын.
қадамымен берілген бірқалыпты айырымдық торының үш тізбектей торабы болсын.
Тейлор қатарын
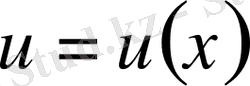 функциясы үшін (1. 5) формуласы арқылы жіктейміз.
функциясы үшін (1. 5) формуласы арқылы жіктейміз.
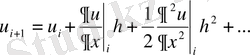 , (1. 5)
, (1. 5)
Егер оның екінші мүшесінен бөліп алсақ, онда (1. 6) формула орынды болады
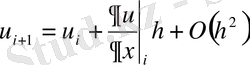 . (1. 6)
. (1. 6)
Демек (1. 7) формуласы орынды,
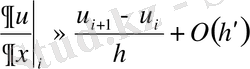 . (1. 7)
. (1. 7)
Интегралдық әдіс. Сызықты Хопфа теңдеуін дивергентті (ажырату) түрде қарастырайық.
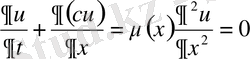
Кеңістікте
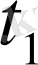 -ден
-ден
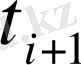 -ге және
-ге және
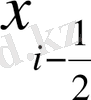 ден
ден
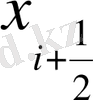 -ге дейін интервалда уақыт бойынша (1. 8) формуласы арқылы интегралдаймыз.
-ге дейін интервалда уақыт бойынша (1. 8) формуласы арқылы интегралдаймыз.
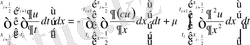 . (1. 8)
. (1. 8)
Жақша ішіндегі өрнектерді интегралдау арқылы төмендегіні (1. 9) аламыз:
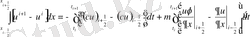 . (1. 9)
. (1. 9)
Қалған интегралдарды - кеңістікті интегралды орта туралы теорема, ал уақыт бойынша интегралды тіктөртбұрыштар (1. 10) формуласы арқылы жуықтап есептейміз.
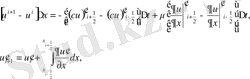 (1. 10)
(1. 10)
(1. 10) қатынасынан орта туралы теораманы қолданудан қалған туындылар (1. 11) формуласының көмегімен аппроксимацияланады (жуықталады) .
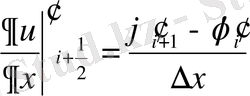 . (1. 11)
. (1. 11)
(1. 11) - ді (1. 10) - ға қою және
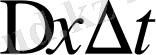 - ке бөлу арқылы (1. 12) айырымдық ұқсастықты аламыз.
- ке бөлу арқылы (1. 12) айырымдық ұқсастықты аламыз.
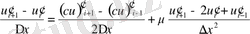 . (1. 12)
. (1. 12)
Көпмүшелілік жуықтау. Айырымдық өрнекті алу әдісі - алдымен тордың торабында мәндері бойынша құрылып, кейін аналитикалы дифференциалданатын тәуелсіз параметрлі аналитикалық аппроксимацияланатын (жуықталатын) функцияларға қолдануға негізделген. Аппроксимацияланушы функцияның түрі жуықтау шешімінен анықталуы керек, бірақ аппроксимацияланушы функция ретінде көпмүшелік қолданылады.
 фукциясының мәні
фукциясының мәні
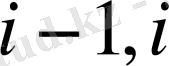 және
және
 нүктелерінде берілсін деп ұйғарайық және
нүктелерінде берілсін деп ұйғарайық және
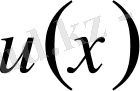 аппроксимация функциясын (1. 13) формуласы арқылы 2-ші ретті көпмүшеге келтіреміз.
аппроксимация функциясын (1. 13) формуласы арқылы 2-ші ретті көпмүшеге келтіреміз.
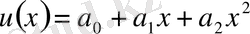 , (1. 13)
, (1. 13)
ыңғайлы болу
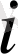 үшін
үшін
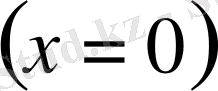 нүктесін координаталар басы деп аламыз. Сонда
нүктесін координаталар басы деп аламыз. Сонда
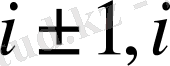 нүктелерінде жазылған теңдеу сәйкесінше (1. 14) формуласында көрсетілген
нүктелерінде жазылған теңдеу сәйкесінше (1. 14) формуласында көрсетілген
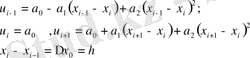 , (1. 14)
, (1. 14)
береді.
Онда (1. 14) формуласы арқылы келесі (1. 15) қатынасты аламыз:
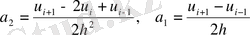 , (1. 15)
, (1. 15)
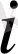 - нүктесінде бірінші және екінші ретті туындылар сәйкесінше (1. 16) арқылы өрнектеледі
- нүктесінде бірінші және екінші ретті туындылар сәйкесінше (1. 16) арқылы өрнектеледі
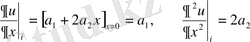 , (1. 16)
, (1. 16)
түрінде болады.
(1. 16) есеп - қитаппен (1. 15) формулалары дәлдіктерімен 2 - ретті орталық айырымдық формулаларымен дәл келеді.
1. 3 Айырымдық схема құрудың вариациялық принципі
Айырымдық схема құру әдісінің ең көп тараған әдісі баланстың әдісі немесе шет ел авторларының термині бойынша «бокс - әдіс ». Баланс әдісі консервативті түрде жазылған және сақталу заңын қанағаттандыратын теңдеулер үшін қолданылады.
Торлық облыстың элементар ұяшығы («бокс») үшін баланс теңдеуінен айырымдық схема құрылады. Бұл жағдайда баланс теңдеуінде ұяшық бойынша интеграл алынады. Элементар ұяшықтар үшін интеграл есептеу әдісіне тәуелді интерполяциялық әдіс баланстық аппроксимацияның бүтін жиынын береді. Солардың ішінде бізді көбірек қызықтыратыны квадраттық шамасын сақтауға келтірілітендері. Мысалы энергиясы, энстрофиясы, сонымен бірге жалпы алғанда әрбір сұлбаны арнайы әдіспен құрып және оны орнықтылыққа зерттейтін энергетикалық баланс қатынасы орнықтылығын есептеуді қамтитындары. Сонымен қатар баланс әдісіне ізделінді функцияның туындысы бар болатын шектік шарттарды аппроксимациялауда қандайда бір қиындықтар туады. Жоғарыда атап кеткен баланс әдісінің шектелген бөлігіне вариациондық жақындауды және аппроксимация құру үшін дифференциалдық теңдеудің өзінен емес оған сәйкестендірілетін интегралдық тепе - теңдіктерді қолдана отырып әлсіздендіруге болады. Мұндай жақындау дифференциалдық теңдеу үшін үзіліссіз және үзілісті коэффициенттер жағдайында шектік және бастапқы шарттар энергетикалық түрде баланстрланған айырымдық аппроксимация құрудың бірыңғай және жеңіл пішінделетін пройедурасын береді.
Жылу өткізгіштік теңдеуінде (1. 17) вариациондық әдісті қолдануды көрсетеміз:
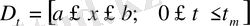 , (1. 17)
, (1. 17)
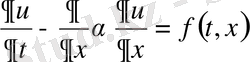 ,
,
мұндағы
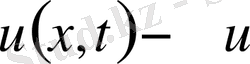 бойынша
бойынша
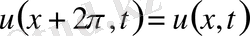 периодтылық шартын және
периодтылық шартын және
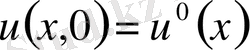 бастапқы шартын қанағаттандыратын температура үлестірілуі. Интегралдық тепе - теңдік құру үшін теңдеуін (
бастапқы шартын қанағаттандыратын температура үлестірілуі. Интегралдық тепе - теңдік құру үшін теңдеуін (
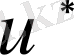 -жатық функциясын)
-жатық функциясын)
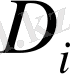 облысында анықталған
облысында анықталған
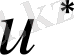 - жатық функциясына көбейтеміз, нәтижені интегралдаймыз, содан (1. 18) формуласы келіп шығады:
- жатық функциясына көбейтеміз, нәтижені интегралдаймыз, содан (1. 18) формуласы келіп шығады:
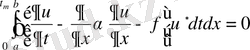 . (1. 18)
. (1. 18)
Бұдан бөліктеп интегралдаудан (1. 19) интегралдық тепе -теңдікті аламыз:
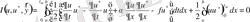 , (1. 19)
, (1. 19)
мұндағы
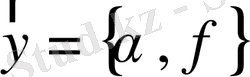 - кіріс параметрлерінің векторы. Торлық облысты бір өлшемді тура көбейтінді көмегімен енгіземіз.
- кіріс параметрлерінің векторы. Торлық облысты бір өлшемді тура көбейтінді көмегімен енгіземіз.
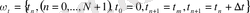 ,
,
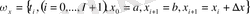 ,
,
және де
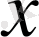 және
және
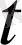 бойынша дәл
бойынша дәл
 - ші ретті аппроксимация класында (1. 19) тепе -теңдінің қосындылы үлгісін (1. 20) формуласы арқылы құрамыз.
- ші ретті аппроксимация класында (1. 19) тепе -теңдінің қосындылы үлгісін (1. 20) формуласы арқылы құрамыз.
 (1. 20)
(1. 20)
Мұндағы
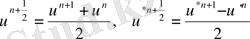 . Егер кез келген
. Егер кез келген
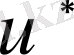 жеткілікті жатық функция болса, (1. 19) көмегімен шектік шарттармен берілген (1. 17) есебінің шешімін әлсіз жалпыланған мағынада (1. 21) формуласымен анықтауға болады.
жеткілікті жатық функция болса, (1. 19) көмегімен шектік шарттармен берілген (1. 17) есебінің шешімін әлсіз жалпыланған мағынада (1. 21) формуласымен анықтауға болады.
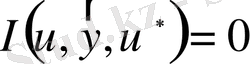 , (1. 21)
, (1. 21)
түріндегі жазуға болатын (1. 19) тепе - теңдігі бастапқы және шекаралық шарттармен дифференциалдық теңдеуді қамтиды.
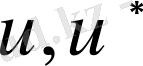 функциялары салыстырмалы түрде (1. 17) және (1. 19) да барлық амалдардың мағынасы болатындай дәрежеде жатық болсын деп ұйғарайық. Жатық болу дәрежесін туындының ретімен және (1. 17) теңдеуімен, (1. 19) интегралдық тепе -теңдігіне кіретін қосындыланатын функциялар дәрежесімен анықталады. (1. 17) теңдеуінен (1. 19) тепе - теңдігі
функциялары салыстырмалы түрде (1. 17) және (1. 19) да барлық амалдардың мағынасы болатындай дәрежеде жатық болсын деп ұйғарайық. Жатық болу дәрежесін туындының ретімен және (1. 17) теңдеуімен, (1. 19) интегралдық тепе -теңдігіне кіретін қосындыланатын функциялар дәрежесімен анықталады. (1. 17) теңдеуінен (1. 19) тепе - теңдігі
 және
және
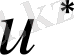 функцияларының компоненттерінен тек қана бірінші туындысы болуымен ерекшеленеді. Функция класының жатық болу қажеттілігінен біршама әлсіретеді, үзіліссіз және үзілісті коэффициентті есептер үшін айырымдық аппроксимация құрудың бір мәнді процедурасы алынады.
функцияларының компоненттерінен тек қана бірінші туындысы болуымен ерекшеленеді. Функция класының жатық болу қажеттілігінен біршама әлсіретеді, үзіліссіз және үзілісті коэффициентті есептер үшін айырымдық аппроксимация құрудың бір мәнді процедурасы алынады.
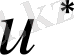 - ны таңдаудың еркіндігін есептей отырып, (1. 19) тепе -теңдігінің айқындалған қасиеттерін белгілейік. Дербес жағдайда,
- ны таңдаудың еркіндігін есептей отырып, (1. 19) тепе -теңдігінің айқындалған қасиеттерін белгілейік. Дербес жағдайда,
 деп алып, (1. 19) - дан (1. 17) есебіне сәйкес (1. 22) жүйе энергиясының баланс теңдеуін аламыз:
деп алып, (1. 19) - дан (1. 17) есебіне сәйкес (1. 22) жүйе энергиясының баланс теңдеуін аламыз:
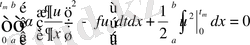 . (1. 22)
. (1. 22)
Айырымдық аппроксимация құру процедурасы келесіден тұрады: Бастапқыда интегралдар квадратуралық формуламен сәйкес
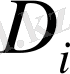 - да аппроксимацияланады, содан кейін айырымдық қатынасқа сәйкес бірінші туындымен алмастырылады. Трапеция немесе центрлік тіктөртбұрыш түріндегі бір өлшемді квадратуралық формулаларды тізбектей қолдану нәтижесінде шығатын (1. 19) қосындылауын тепе - теңдігінің сол жағын қарастыра отырып
- да аппроксимацияланады, содан кейін айырымдық қатынасқа сәйкес бірінші туындымен алмастырылады. Трапеция немесе центрлік тіктөртбұрыш түріндегі бір өлшемді квадратуралық формулаларды тізбектей қолдану нәтижесінде шығатын (1. 19) қосындылауын тепе - теңдігінің сол жағын қарастыра отырып
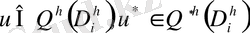 және
және
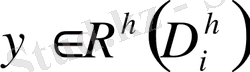 торлық функция кеңістігінде
торлық функция кеңістігінде
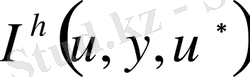 функционалы
функционалы
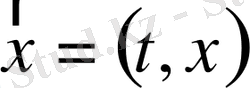 нүктесіндегі
нүктесіндегі
 функциясының торлық компоненті кез келген және тәуелсіз вариациаларды
функциясының торлық компоненті кез келген және тәуелсіз вариациаларды
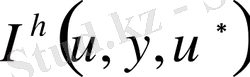 функционалының тұрақтылық шартынан айырымдық теңдеу үшін
функционалының тұрақтылық шартынан айырымдық теңдеу үшін
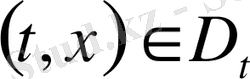 нүктесіндегі (1. 23) нақты өрнегін алуға болады, яғни :
нүктесіндегі (1. 23) нақты өрнегін алуға болады, яғни :
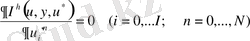 , (1. 23)
, (1. 23)
(1. 19) аппроксимациясының қателігі әлсіз мағынада екі
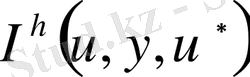 және
және
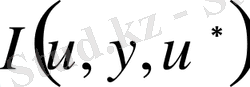 функционалының жақындық дәрежесімен түсіндіріледі және квадратуралық формуланың қалдық мүшелерімен және бірінші туындылы айырымдық өрнек ауыстырымының қателігімен бірге сипатталады. (1. 23) - ке дифференциалдау амалын формальді түрде орындау арқылы бірнеше түрлендіруден кейін келесі (1. 24) теңдеулер жүйесіне келеміз:
функционалының жақындық дәрежесімен түсіндіріледі және квадратуралық формуланың қалдық мүшелерімен және бірінші туындылы айырымдық өрнек ауыстырымының қателігімен бірге сипатталады. (1. 23) - ке дифференциалдау амалын формальді түрде орындау арқылы бірнеше түрлендіруден кейін келесі (1. 24) теңдеулер жүйесіне келеміз:
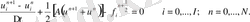 (1. 24)
(1. 24)
Мұндағы
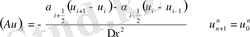 .
.
1. 4. Шектік - айырымдық теңдеулер
Шектік - айырымдық жақындау сәйкестенділетін дифференциалдық теңдеулерде туындыны ауыстыру арқылы алынатын алгебралық теңдеулер осы дифференциалдық теңдеудің шектік - айырымдық аппроксимациясы немесе шектік - айырымдық схемасы деп аталады. Бұл тақырыпта аппроксимация қателігі және шектік айырымдық сұлбасының дәлдігі жайлы қарастырамыз. Мысал ретінде (1. 25) формуласы арқылы сызықты адвекция теңдеуін қолданамыз:
 , (1. 25)
, (1. 25)
мұндағы
 - оң тұрақты. (1. 25) теңдеуі
- оң тұрақты. (1. 25) теңдеуі
 айнымалысының
айнымалысының
 тұрақты жылдамдықпен
тұрақты жылдамдықпен
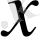 осіне оң бағытпен адвекциясын бейнелейді. Бұл қарапайым теңдеуді аналитикалық түрде шешуге болады. Алдымен аналитикалық шешімдерін анықталған нақты шешімдер қасиеттерін салыстыру жолымен сандық шешімдер қасиеттерін зерттеу үшін аламыз. Осы мақсатпен
осіне оң бағытпен адвекциясын бейнелейді. Бұл қарапайым теңдеуді аналитикалық түрде шешуге болады. Алдымен аналитикалық шешімдерін анықталған нақты шешімдер қасиеттерін салыстыру жолымен сандық шешімдер қасиеттерін зерттеу үшін аламыз. Осы мақсатпен
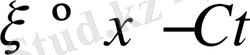 ауыстыру жолымен
ауыстыру жолымен
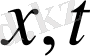 айнымалысынан
айнымалысынан
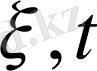 айнымалысына көшу ыңғайлы.
айнымалысына көшу ыңғайлы.
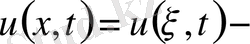 белгілеуін пайдаланып,
белгілеуін пайдаланып,
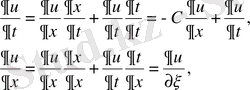
аламыз. Бұл өрнектерді (1. 25) - ке апарып қойсақ
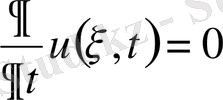 аламыз. Осылайша
аламыз. Осылайша
 функциясы уақыт функциясы бола алмайды, бірақ
функциясы уақыт функциясы бола алмайды, бірақ
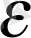 үшін кез келген функция болуы мүмкіндігі көрініп түр. Осылайша (1. 25) теңдеуінің шешімі
үшін кез келген функция болуы мүмкіндігі көрініп түр. Осылайша (1. 25) теңдеуінің шешімі
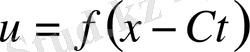 болады. Мұндағы
болады. Мұндағы
 - кез келген функция. Бұл кез келген бастапқы
- кез келген функция. Бұл кез келген бастапқы
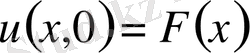 шартын қанағаттандыратын (1. 25) адвекция теңдеуінің жалпы шешімі. Осылайша
шартын қанағаттандыратын (1. 25) адвекция теңдеуінің жалпы шешімі. Осылайша
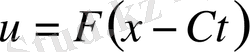 бастапқы шартын қанағаттандыратын (1. 25) теңдеуінің шешімі болып табылады. Физикалық түсіндіруде шешімді
бастапқы шартын қанағаттандыратын (1. 25) теңдеуінің шешімі болып табылады. Физикалық түсіндіруде шешімді
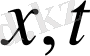 жазықтығында қарастыру ыңғайлы. Бұл жағдайда түзу сызық бойында (1. 26) тұрақты мән қабылдайтыны айқын.
жазықтығында қарастыру ыңғайлы. Бұл жағдайда түзу сызық бойында (1. 26) тұрақты мән қабылдайтыны айқын.
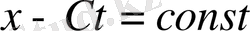 . (1. 26)
. (1. 26)
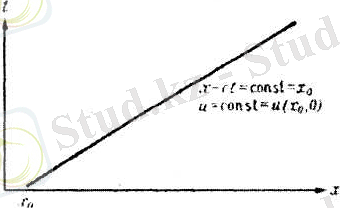
Бұл түзулер адвекция теңдеуінің сипаттамалары болып табылады. Солардың бірі (сурет-1. 1) көрсетілген. Шешімдер осы характеристикалар бойымен жалғасады. Енді торлық әдіспен (1. 25) теңдеуінің жуық шешімін табу үшін схема құрамыз. Біз қазір тек қана (сурет-1. 2) - да бейнеленген тор көмегімен алынған
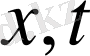 жазықтығындағы нүктелер дискретті жүйесінде жуық шешімін қарастырамыз.
жазықтығындағы нүктелер дискретті жүйесінде жуық шешімін қарастырамыз.
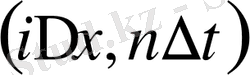 -нүктесіндегі жуық шешім
-нүктесіндегі жуық шешім
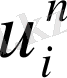 арқылы белгіленген.
арқылы белгіленген.
 жазақтығына характеристика бойымен жалғасатын нақты шешімдегі беталыс жақындау теңдеуін құру ойын тудырады. Мысалға туындының уақыт бойынша ауысу жолымен айырымдық қатынасты - алға бағытымен, ал кеңістіктегі туындылы - айырымдық қатынасты артқа бағытымен алайық. Нәтижеде келесі сұлбаны аламыз.
жазақтығына характеристика бойымен жалғасатын нақты шешімдегі беталыс жақындау теңдеуін құру ойын тудырады. Мысалға туындының уақыт бойынша ауысу жолымен айырымдық қатынасты - алға бағытымен, ал кеңістіктегі туындылы - айырымдық қатынасты артқа бағытымен алайық. Нәтижеде келесі сұлбаны аламыз.
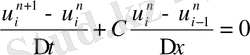 Equation. 3 .
Equation. 3 .
Сурет 1. 1 - Сызықты адвекция теңдеуінің характеристикаларының бірі
Бұл схема «ағынға қарсы» деп аталуы мүмкін. Соңғы сөз
 нүктесінің орналасуы адвекция жылдамдығы салыстырмалы екендігін көрсетеді. Бұл әлбетте берілген дифференциалдық теңдеу үшін шексіз көп шектік - айырымдық сұлбалардың ішіндегі біреуі ғана.
нүктесінің орналасуы адвекция жылдамдығы салыстырмалы екендігін көрсетеді. Бұл әлбетте берілген дифференциалдық теңдеу үшін шексіз көп шектік - айырымдық сұлбалардың ішіндегі біреуі ғана.
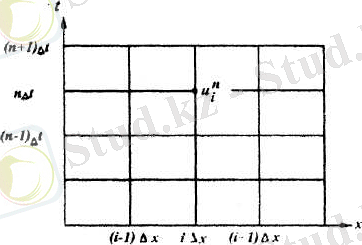
Сурет 1. 2 - Адвекция теңдеуі жуық шешімін анықтау үшін ақырлы -
айырымдық сұлба
 өсімшелері нольге ұмталғанда осы дифференциалдық теңдеуге жуықталатын көптеген (1. 27) формуласындағыдай сұлбалар бар.
өсімшелері нольге ұмталғанда осы дифференциалдық теңдеуге жуықталатын көптеген (1. 27) формуласындағыдай сұлбалар бар.
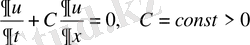 , (1. 27)
, (1. 27)
(1. 27) тасымалдау теңдеуіне (1. 28) формуласы орындалады
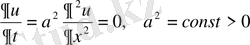 , (1. 28)
, (1. 28)
диффузия теңдеуіне гидрогазодинамика теңдеуі үшін модельді болатын айырымдық схема құру әдістерін қарастырамыз. Ең қарапайым әдіс - айырымдық аппроксимациямен теңдеуге енетін туындылы ауыстырымнан тұрады.
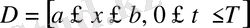 тіктөртбұрышында бірқалыпты айырымдық торды енгіземіз.
тіктөртбұрышында бірқалыпты айырымдық торды енгіземіз.
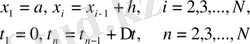
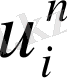 арқылы
арқылы
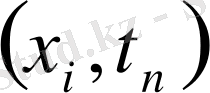 торабындағы
торабындағы
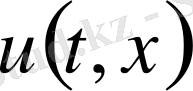 функцияның мәнін белгілейміз. Келесі (1. 29) айырымдық схеманы қарастырайық:
функцияның мәнін белгілейміз. Келесі (1. 29) айырымдық схеманы қарастырайық:
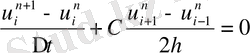 , (1. 29)
, (1. 29)
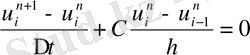 , (1. 30)
, (1. 30)
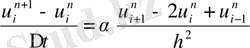 . (1. 31)
. (1. 31)
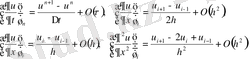
болғандықтан (1. 29) және (1. 31) сұлбалары (1. 27) - (1. 28) теңдеулерін
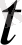 бойынша бірінші ретті,
бойынша бірінші ретті,
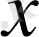 бойынша екінші ретті аппроксимациялайды. (1. 30) схемасы (1. 32) теңдеуін
бойынша екінші ретті аппроксимациялайды. (1. 30) схемасы (1. 32) теңдеуін
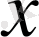 және
және
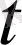 бойынша бірінші ретті аппроксимациялайды:
бойынша бірінші ретті аппроксимациялайды:
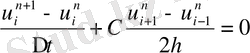 , (1. 32)
, (1. 32)
(1. 27) теңдеуі үшін
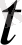 және
және
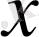 бойынша екінші ретті схема болып табылады. Бір белгілі және бір белгісіз уақыттық қабатта белгісіз функцияның мәні бар сұлбалар екіқабатты деп аталады. Демек, (1. 29) - (1. 31) екіқабатты, ал (1. 32) үшқабатты .
бойынша екінші ретті схема болып табылады. Бір белгілі және бір белгісіз уақыттық қабатта белгісіз функцияның мәні бар сұлбалар екіқабатты деп аталады. Демек, (1. 29) - (1. 31) екіқабатты, ал (1. 32) үшқабатты .
Анықтама: Келесі қабатта функцияның бір ғана мәні болатын әрбір теңдеудегі схема айқын деп аталады. Кері жағдайда схема айқындалмаған болып табылады.
Жоғарыда қарастырылған схемалар - айқын схема (1. 27) теңдеуіне айқындалмаған схеманың мысалы ретінде келесі (1. 33) теңдеуін көрсетуге болады
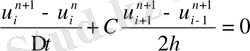 , (1. 33)
, (1. 33)
алуға болады. Жартылай айқындалмаған екі қабатты схемалар класын (1. 34) теңдеуі арқылы қарастырамыз:
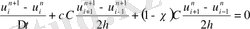 . (1. 34)
. (1. 34)
Мұндағы
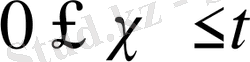 - параметр.
- параметр.
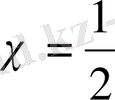 -болғанда
-болғанда
 бойынша
бойынша
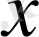 - бойынша да екінші ретті аппроксимация схемасын аламыз. Жоғарғы ретті аппроксимацияның екіқабатты айқын схемасын құру әдістерінің бірі айырымдық схемаларды дифференциалдық берілгендерге қолданылатын әдіс болып табылады.
- бойынша да екінші ретті аппроксимация схемасын аламыз. Жоғарғы ретті аппроксимацияның екіқабатты айқын схемасын құру әдістерінің бірі айырымдық схемаларды дифференциалдық берілгендерге қолданылатын әдіс болып табылады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz