Қорларды және ақша қорларын басқарудағы стохастикалық модельдер: теориясы, типтері және қолдану мүмкіндіктері


Қорларды басқарудағы стохастикалық модельдер
Жоспар
Кіріспе
Бөлім 1. Қорларды басқарудағы модельдер
- Модельдердің түсінігі, типтері4
- Детерминантты модельдер. . 8Статикалық модельдер8Динамикалық модельдер. 13
Бөлім 2. Қорларды басқарудағы стохастикалық модельдер
- Кездейсоқ модельдер түсінігі. . 19
- Стохастикалық модельдер . . . 23Бір этапты модельдер . . . 23Көп этапты модельдер. . 29
Бөлім 3. Стохастикалық модельдермен ақша қорларын басқару
3. 1. Ақша қорларын басқару . . . 35
3. 2. Миллер-Орр моделін ҚР-да қолдану мүмкіндігі42
3. 3. Дамымаған нарық жағдайындағы модель. . 47
Қорытынды
Қолданылған әдебиеттер тізімі
Кіріспе
Қазіргі таңда шаруашылықтағы қорларды басқару мәселесінің ағуалдығын жоғары дәрежеде қарастырылады, өйткені қорлардың өзі өндірістік процестерде немесе ағымдарда ең маңызды факторлар қатарына жатқызылады. Қорларды сақтау шығындары үлкен болуы мүмкін болады. Егер қорлардың көлемі үлкен болса, ол кірістердің барлық дәрежелерін жоққа шығарады. Ал егерде қорлардың көлемі төмен дәрежеде болса, шаруашылықтың тіршілік ету тәуекелдігі жоғарылайды. Қорлардың деңгейі мүлдем бітсе, кәспорын өз алдына қойылған мәселелерінің орындалмауына әкеліп соқтырады. Сонымен қатар қорларды басқарудағы ең басты назар аударатын жай бұл шығынсыз жалпы оптималды стратегия ойлап табу. Көптеген оқулықтарда осы оптималды стратегия іздеу мақсатында көптеген моделдерді қарастырып өткен, бірақ та моделдердің көбісін детерминантты немесе бәріне мәлім жағдайға келтіріп жазады. Мүмкін кітапта бұндай жайдың жазылғаны дұрыс шығар, бірақ нақты практикада кей кезде немесе тіпті мүлдем кездейсоқ жағдайларға тап боламыз. Сондықтан көптеген экономистердің және математиктердің теорияларында кездейсоқ жағдайын ағуалды да, күрделі мәселе деген.
Қорларды біз бір белгілі ресурстарды, шикізаттарды, тауарларды жатқызамыз. Осы қорлар арқылы болашақтағы қажеттіліктерді қанағаттандыруымызға арналған. Сонымен қатар қорларға ақшалай қаражаттарды жатқызуымызға болады. Осы қорлардың сипатына байланысты оларды қандай тұрғыда келуін анықтаймыз. Жалпы қорларды басқаруда екі тұрғыда қарастыруымызға болады: біріншісі жаңа айтып кеткендей бұл детерминантты, ал екіншісі кездейсоқты. Біріншісі арқылы ақша немесе тауар қозғалыстарын анализдеуге болады, бірақта нарықтық экономикада, яғни айналамыздағы күрт өзгермелі процестердің арасында қорларды тиімді басқару мүмкіндігі жоқ. Сондықтан күрт өзгермелі кезеңінде өте тиімді моделдер қажеттілігі туындап отыр. Осындай модельдер қатарына кездейсоқ немесе стохатикалық модельдерін жатқызамыз.
Негізі бітіру жұмысының басты мақсаты осы кездейсоқ модельдердің қазіргі нақты практикада қолданылуының мүмкіндігін ашып, оларға түсініктеме беріп, қысқаша анализдеп бір белгілі айтқан проблемаларды шешуге жолдар табуы болып отыр.
Бөлім 1. Қорларды басқарудағы модельдер
- Модельдердің түсінігі, типтері
Кез келген қорларды басқару моделі жалпы екі сұраққа жауап береді:
- Қанша өнім көлеміне заказ беру ?
- Қашан заказ беру ?
Бірінші сұрақтың жауабы заказды орналыстыратын кезінде қажетті оптималды ресурстар мөлшерін анықтайтын заказ көлемі арқылы көрсетіледі. Әртүрлі ситуацияға байланысты заказ көлемі уақыт бойынша өзгереді. Ал екінші сұрақ жауабы қорларды басқару жүйесінің типіне байланысты. Егер жүйе бойынша қордың жағдайын бірдей уақыт аралығында периодты бақылау жүргізілсе, онда жаңа заказдың түсуі көбінесе әр уақыт интервал басымен сәйкес келеді. Егер де жүйе бойынша қор жағдайында үздіксіз бақылау болса, онда жаңа заказ орналастыру қажеттілігі кезіндегі қор деңгейімен анықталатын заказ нүктесі болады.
Сонымен қорды басқарудағы есепті шешуі келесідей болады:
- Қор жағдайын периодты бақылаукезінде жаңа ресурстар санын жеткізуінзаказ мөлшеркөлемінде бірдей уақыт аралығында жеткізілуі тиіс.
- Қор жағдайын үздіксіз бақылаукезінде жаңа заказдықор көлемімөлшерінде, оның деңгейізаказ нүктесінежеткенде орналастырылуы керек.
Заказдың мөлшерін және нүктесін қорды басқару жүйесіндегі жалпы шығындардың соммасын минимизациялаған жағдайында анықтайды. Осыны функцияда екі айнымалы арқылы көрсетуге болады. Қорды басқару жүйесіндегі жалпы шығындардың соммасы функция түрінде былай:
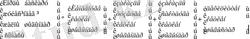
Иемдену шығындары өнім бірлігінің бағасы заказ мөдшеріне байланысты кезінде маңызды фактор болады. Өнімнің бірлік бағасы төмендегенде заказ мөлшері жоғарлағанын көбінесе түгелдей жеңілдік түрінде бейнелейді. Заказды түзеуге кеткен шығындар орналастыруға байланысты кеткен тұрақты шығындары болып көрсетіледі. Қорды сақтауға кеткен шығындар қорды қоймада сақтау шығыстары. Дефициттен кеткен шығыстар қажетті өнім қорының жоқшылығынан шығатын шығыстар.
1-ші суретте төрт шығындардың байланысы көрсетілген. Қордың оптималды деңгейі шығындардың жалпы шығындардың минимумына сәйкес келеді. Тағы да айта кететін бір жай қорды басқару моделінде барлық төрт шығындардың болуы міндет емес, себебі олардың кейбіреулері өте кішкене мөлшерін қабылдап, барлығының кірістіруін жалпы шығындар функциясын күрделірендіреді. Практикада шығындардың кейбір компоненталарын есепке алмайды, өйткені үлесімді мәнін қабылдамағандықтан. Бұндай факторды тек әртүрлі моделдерді қарастырғанда байқауға болады.
Қорды басқарудағы моделдердің типтері оның сұранысының қандай болуына байланысты болады. Негізі сұраныс детерминанты (бәріне мәлім) немесе кездейсоқ (кездейсоқ тығыдығымен берілетін) болады. 2-ші суреттегідей қорды басқарудағы моделдердің сұраныс бойынща жіктелуі. Детерминантты сұраныс статикалық болуы мүмкін, яғни тұтыну қарқындылығы уақыт өтуіне қарай өзгеріссіз. Немесе динамикалық , яғни сұраныс мәлім болып, бірақ уақыт өтуіне қарай өзгереді. Кездейсоқ сұраныс стационарлы болуы мүмкін, яғни сұраныстың кездейсоқ функциясының тығыздығы уакқыт өтуіне байланысты өзгеріссіз. Немесе стационарлы емес , яғни сұраныстың кездейсоқ функциясының тығыздығы уакқыт өтуіне байланысты өзгереді.
Нақты жағдайда детерминантты статикалық сұраныс жағдайы сирек кездеседі. Бұндай жағдайды қарапайым деп қарастыруымызға болады. Мысалыға көп тұтынатын өнімдер, нан сияқты сұранысы күнделікті өзгеруі мүмкін. Осы өзгерістердің мәні кішкене болғандықтан, ұсыныстың статикалық болуы нақтылықты аса үлкен әсер етпейді.
Сұранысқа өмірде нақтырақ сипаттама беретін кездейсоқ стационарлы емес бөлу мүмкін береді. Бірақ та мактематикалық тұрғыда қарастырғанда модел уақыт өтуіне қарай күрделене түседі. 2-ші суретте моделдердің детерминнанты жағдайдан кездейсоқ жағдайға өткенде математикалы күрделенеді. Әрине суреттегі жіктелуді абстрактылы деңгей десекте болады.
Бірінші деңгейде сұраныстың кездейсоқ бөлінуі уақытқа стационарлы дейді. Бұл дегеніміз сұранысты зерттеліп отырған барлық уақыт периодтарында кездейсоқтылықты бөлу функциясын қолданады. Осы жағдайда сұранысқа маусымдық ауытқулар моделдер есепке алынбайды.
Абстаркцияның келесі деңгейінде сұраныстың бір периодтан екінші периодқа өткендегі өзгерісін есепке алады. Бірақта бөлу функциясы қолданылмай, әр периодтағы тұтынушылық сұраныстың орта мәнімен беріледі. Бұндай қарапайымдылыққа көшу деген қорды басқарудағы тәуекелділік элементі саналмайды. Бірақтан бұл кездейсоқ моделде аналитикалық және есептеулік қасиеттеріне күрделі болуы болмай, сұраныстың маусымдық тербелістерін анықтай аламыз. Басқа сөзбен екі жағдайды қарастыра аламыз: бір жағынан кездейсоқтың стационарлы бөлінуін және екінші анықталғандық жағдайлары.
Үшінші деңгейде каракпайым қылу және сұраныс өзгеруін тәуекелділік элементі ретінде алып тастайды. Сонымен сұраныс барлық периодтарда орташа мәнге ие болады. жалпы сұранысты тұрақты дейміз.
Сұраныс қорды басқару моделін құрастыруында негізгі фактор болса да, басқа факторлар көмегімен құратыра аламыз. Оларға кіреді:
- Тасымалдаудың кешіктіруі немесе заказдардың орындау мерзімдері. Заказды орналастырғаннан кейін тасымалдау сол мезетте немесе оған біршама уақыт қажет етеді. Орналастыру және тасымалдау арасындағы мезетті тасымадаудың кешіктіруі дейді. Бұл мән детерминантты немесе кездейсоқ болуы мүмкін.
- Қордың толуы. Қорды басқару жүйесі тасымалдаудың кешіктіруімен қызмет ете алатын болса да, қордың толуы сол мезетте немесе тең уақыт аралығында жүреді. Қордың толуы сол мезетте болған жағдайда заказдар көбінесе сыртқы көздерден келеді. Ал тең уақыт аралығында қордың толуы сол кәсіпорынның қоймасынна алынады. жалпы жағдайда жүйе тасымалдаудың кешіктіру және тең уақыт аралығында қордың толуы жұмыс істейді.
- Уақыт аралығы бұл қордың деңгейін реттеуге кеткен интервалы. Уақыт аралығына байланысты сенімді болжауға мүмкіндік, қарастырылып отырған период шекті және шексіз.
- Қор жинау пунктардың саны. Қорды басқару жүйесіне бірнеше қор жинау пункиттары кіруі мүмкін. Бұндай пункттардың ұйымдастырылуы біреуі жеткізуші екіншісі қабылдаушы болады. Схема әртүрлі деңгейде құрастырылады, сондықтан жеткізуші пункт қабылдаушы пункт болып істей береді. Онда қорды басқару жүйесі кең тарапты дейміз.
- Өнім түрлерінің саны. Қорды басқару жүйесінде бірнеше өнім түрлері болуы мүмкін. Бұл фактор бір өнімнің екінші өнімге байланысынан туады. Бір өнімдерге арнайы қойма қажет ал басқасы тура өндірісте өндрірліп, өндіріс қорында шектеледі. Детерминантты модельдер
Нақты өмірде барлық жағдайларға және қасиеттерге ие болатын бәріне мәлім қорды басқарудағы моделді құру өту қиын. Бірақ та бір әмбебап модель құра алсақ та, он аналитикалық түрде қарастырғанда шешілуге мүмкін емес. Келесі қарастыратын моделдердің түрлері қорды басқару моделдер жүйесіне жатады. Бұл моделдер нақты өмірде қолданылуы мүмкін емес болса да, олар бізге қорды басқарудағы моделдерге жалпы түсінігін ашуға мүмкіндік береді.
Келесі қарастыратын моделдер детерминантты моделдер қатарына жатады. Моделдердің көбісі бірөнімді, тек біреуі ғана өзара бәсекелесетін бірнеше өнімді модел. Олардың арасындағы ең басты айырмашылығы сұраныстың статикалық немесе динамикалық болуы. Сонымен қатар тағы бір фактор ол шығындар функциясының құрылуы. Оптималды шешім табуға көптеген классикалық схемалар қолданылады. Бұл мысалдар қорды басқарудағы оптималдылықты табу үшін әртүрлі әдістерді қолдануы керектігін көрсетеді.
1. 2. 1 Статикалық модельдер
Бір өнімді статикалық моделдер
Қорды басқарудағы моделдің қарапайым түрінде сұраныстың уақыт өтуіне қарай өзгермей, қордың тез арада толуы және дефициттің жоқ болуы арқылы жүреді. Бұндай моделдерді келесі жағдайларда қолдануға болады:
- Ғимараттарда түнгі шамдарды қолдануға;
- Канцерлярлық тауарларды, бұл қағаз, блокноттар және қарындаштарды үлкен фирмамен қолдануға;
- өндірістік өнімдерді, бұл болт және гайка, қолдануға;
- тағам ретінде тұтынатын тауарлар.
3-ші суретте қор деңгейінің уақыт өтуіне қарай өзгеруі берілген. Сұраныстың қарқындылығы b -ға тең. Қор ең жоғары мәнге заказды у мөлшерінде тасымалдағаннан кейін жетеді. Қордың деңгейі у мөлшерлі заказды қабылдағаннан кейін у/b уақыты өткеннен кейін нөлге тең болады.
У мөлшерлемесі неғұрлым кіші болса, соғұрлым жаңа заказдарды орналастыру қажет. Бірақ та қордың орташа деңгейі азая береді. Басқа жағынан заказдың мөлшері үлкейген сайын қордың деңгейі жоғарылап, бірақ заказдар сирек орналастырады ( Сурет 4 . ) . Өйткені шығындар заказды орналастыру жиілігіне және сақтаудағы қордың көлеміне тәуелді, онда у мөлшері екі шығындардың арасынан шығады. Бұл қорды басқарудағы моделдің негізінде жатыр.
h - уақыт бірлігіндегі орналастырғанда және болжағанда К - заказды түзетуге кеткен шығын болсын. Онда жалпы соммалы шығындарды былай жазсақ болады TCU (y) . У функциясы арқылы бұл мынандай түрге келеді:
TCU (y) = бір бірлік уақытындағы түзетуге кеткен шығын
+ бір бірлік уақытындағы қорды сақтаудағы шығын =
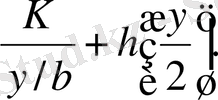
3-ші суреттен көрініп тұрғандай заказ қозғалыс циклінің мерзімі t = y/b және қордың орташа деңгейі у/2 тең.
У мәнінің оптималды болуы TCU (y) -дың у арқылы минимизациялағанда шығады. Сондықтан у - ті үздіксіз айнымалы деп,
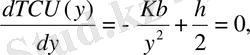
Осыдан заказ мөлшерінің оптималды мәні анықталады
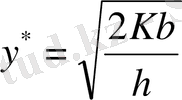
Жоғарыдағы заказ мөлшеріне алынған тұжырымдаманы Уилсондық заказының экономикалық мөлшерлемесі дейді.
Моделдің оптималды стратегиясы өнімнің у* бірлік заказы әр t*=y*/b бірлік уақытысында. Оптималды шығындар TCU (y*), қойылымдардан
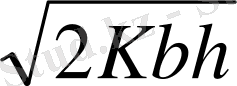 шығады.
шығады.
Көптеген нақты жағдайларда закады орындау мерзімі L бар, ол орналастыру мезетінен нақты тасымалдағанға дейін болады. Әр заказды орналастыру стратегиясында жаңартылу нүктесі болуы қажет. 5-ші суретте жаңартылу нүктесі L -мезетке күтілім тасымалдаудан тезірек болу керек. Практикалық максаттарда заказды жаңартылу нүктесін қордың деңгейі арқылы өзгертуге болады. Практикада келесі жаңартылу нүктесіне жеткенше қор деңгейін үздіксіз бақылайды. Мүмкін осы себептен заказдың экономикалық мөлшерлеме моделін заказ жағдайын үздіксіз бақылау моделі дейді.
Бір өнімді баға айырмашылықты статикалық моделі
Басында қарастырып өткенде тауарды сатып алуға кеткен шығындарды есепке алған жоқпыз. Бірақтан көбінесе өнім бірлігінің бағасы партия мөлшеріне байланысты болып келеді. Бұндай жағдайда бағалар секірмелі түрге келіп немесе жеңілділіктер беріледі. Сонымен қатар қорды басқарудағы моделде сатып алу шығынын ескеру қажет.
Ал енді дефицит жоқ және қордың тез толуы кезіндегі қорды басқарудағы моделін байқап көрейік. Өнімнің бір бірлік бағасын с1, у<q жағдайында с2 - ге тең, y>q жағдайында, мұндағы с1>c2 және q - заказ мөлшері, осы өскен кезінде жеңілдік беріледі дейік. Сонда жалпы соммалық шығын цикл бойында түзетуге кеткен шығын және сақтау шығынын санамағанда сатып алу шығынын қосу керек.
жалпы шығын бір уақыт бірлігінде у<q жағдайында тең
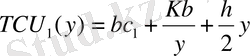
y>q жағдайында шығындар
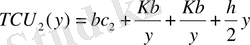
Бұл екі функцияның графигі
6-шы суретте
көрсетілген.
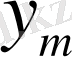 заказ мөлшері деп, осы жағдайда TCU1 және TCU2 минимум мәнге ие. Онда
заказ мөлшері деп, осы жағдайда TCU1 және TCU2 минимум мәнге ие. Онда
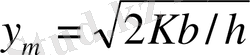
TCU1 және TCU2 шығындар функциясынан (Сурет 6. ) шығатыны
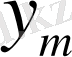 заказдың мөлшерлемесінің оптималдылығы тәуелді болып, суреттегі үш аймаққа қатынасы 1, 2, 3 бағаның айырмашылығынан q тұрады. Бұл аймақтар q(>
заказдың мөлшерлемесінің оптималдылығы тәуелді болып, суреттегі үш аймаққа қатынасы 1, 2, 3 бағаның айырмашылығынан q тұрады. Бұл аймақтар q(>
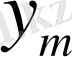 ) теңдеуінен анықталады
) теңдеуінен анықталады
TCU1(
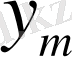 ) =TCU(
) =TCU(
 )
)
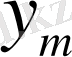 - мәні берілгендіктен теңдеуден шығатын мәні мынаған тең
- мәні берілгендіктен теңдеуден шығатын мәні мынаған тең
 . Онда аймақтар былай анықталады:
. Онда аймақтар былай анықталады:
Аймақ 1: 0<q<
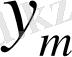 ,
,
Аймақ 2:
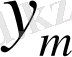 <q<
<q<

Аймақ 3: q<
 .
.
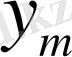
Қойманың көлемі шектеулігі бар көп өнімді статикалық модель
Бұл модел қорды басқару моделдер жүйесіне арналған көп өнімді ауданы шектеулі қоймада сақтау моделі. Берілген жағдай өнімдердің түрлерінің арасындағы байланысты анықтап, модел ішінде шектеулер түрінде келеді.
А- қойма ауданы максимум бола алатын көп өнімді n қойма болсын делік; i - түрлі өнімнің сақталынатын қоймасының ауданы ai тең дейік. Егер уi - бір өнімнің заказының мөлшері болса, онда қоймаға қажеттілік шектеулігі былай:
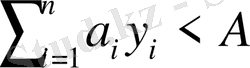
Әр өнімнің қоры тез толып және баға жеңілдіктер жоқ делік. Әрі қарай дефицит жоқ дейік. bi, Ki, және hi - сұраныс қарқындылығы, заказды түзетуге кеткен шығын және бір бірлік өнімді сақтауға кеткен шығын болсын. жалпы әр өнімнің шығындары бір өнімді моделдегі сияқты болады. Сондықтан қарастырылып отырған есеп мынандай түрге келеді:
Минимизациялау TCU(y, …, yn ) =
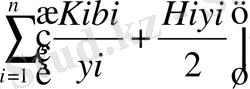 жағдайында
жағдайында
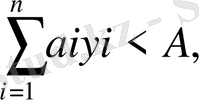 yt>0 барлық i-ге.
yt>0 барлық i-ге.
Осы есептің жалпы шешімі Лагранж көптік әдісімен анықталады. Осы әдіспен шығар алдында оның шектеулері сәйкес келуін көреміз:
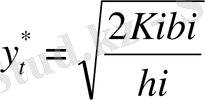
Егер шектеу орындалса, онда оны қолдануға болады.
Шектеу егер
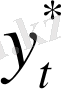 мәні орындалмаса жұмыс істейді. Онда шектеуді қанағаттындыратын жаңа оптималды мәнін уt табу керек. Бұл нәтиже Лагранж функциясын құрудан шығады
мәні орындалмаса жұмыс істейді. Онда шектеуді қанағаттындыратын жаңа оптималды мәнін уt табу керек. Бұл нәтиже Лагранж функциясын құрудан шығады
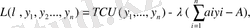
мұндағы
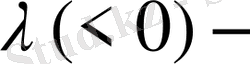 Лагранж көпігі.
Лагранж көпігі.
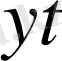 және
және
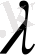 оптималды мәндерін туындыларын нөлге теңестіріп табуға болады. Онда
оптималды мәндерін туындыларын нөлге теңестіріп табуға болады. Онда
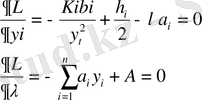
Екінші теңдеуден
 мәнін қойманың шектеулігінің теңдеулерін теңестіруінен аламыз.
мәнін қойманың шектеулігінің теңдеулерін теңестіруінен аламыз.
Бірінші теңдеуден
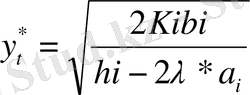
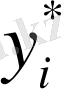 мәні
мәні
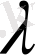 көптігінің
көптігінің
 оптималды мәніне тәуелді.
оптималды мәніне тәуелді.
 мәнін теру және қателер систематикалық әдісімен табуға болады.
мәнін теру және қателер систематикалық әдісімен табуға болады.
1. 2. 2 Динамикалық модельдер
Бір өнімді N-этапты динамикалық модель
Бұл моделде сұраныс мәлім болса да, бірақ этаптаптан этапқа өткенде өзгереді. Қордың деңгейі периодты бақыланады. Тасымалданудың кешіктіруі мүмкін болып, қордың толуы тез арада әр этаптың басында жүреді. Дефицит жоқ болады деп есептелелінеді.
Детерминантты динамикалық моделді құруын зерттеу уақыттың соңына келтіреді. Бұл қажетті сандық шешімдер алу үшін динамикалық программалаудағы әдістерді қолданып, дәл осы жағдайда шектеулі этаптар көмегімен шығарылады. Бірақта сұраныс алдағы периодтарда өзгерседе аса үлкен әсер алып келмейді, сонымен соңғы уақытта кедергі болмайды. Сонымен қатар өнім қорда шексіз сақталынбайды.
Ол үшін i, i=1, 2, …, N, этаптарындағы өлшемдерді анықтайық:
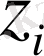 - заказ мөлшері,
- заказ мөлшері,
 - өнімге қажеттілік немесе сұраныс,
- өнімге қажеттілік немесе сұраныс,
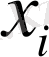 - бастапқы қор,
- бастапқы қор,
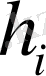 - бір бірлік қорды сақтау шығыны,
- бір бірлік қорды сақтау шығыны,
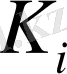 - түзету шығыны,
- түзету шығыны,
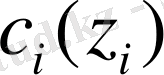 - шекті шығындар функциясы.
- шекті шығындар функциясы.
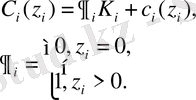 мұндағы
мұндағы
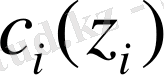 функциясы бір бірлік сатып алу шығындары уақытқа байланысты өзгерсе немесе бағалық айырмашылық болған кезде ағуалды болады.
функциясы бір бірлік сатып алу шығындары уақытқа байланысты өзгерсе немесе бағалық айырмашылық болған кезде ағуалды болады.
Дефицит жоқ болғандықтан жалпы шығындарды заказды түзетуге кеткен, сатып алуға кеткен және сақтау шығындарын минимизациялайтын
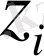 мәнінің оптималды табу керек. Сақтау шығындары мәніне пропорционалды
мәнінің оптималды табу керек. Сақтау шығындары мәніне пропорционалды
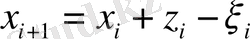
бұл i этаптан i+1 этапқа өткендегі қор көлемі. жалпы
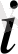 этаптағы сақтау шығыны
этаптағы сақтау шығыны
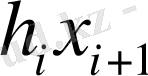 тең. Бұндай түрлендіру моделді жеңілдету мақсатында жасалынады. Динамикалық программалау моделі жеңілдетіледі, егер оны схема түрінде көрсетсек
сурет 7
. Әр қадам этапқа сәйкес келеді. Кері рекуррентті теңдеуін қолдана, әр қадамды i болатын жүйенің жағдайларын анықтайық. i, i+1, …, N этаптарындағы
тең. Бұндай түрлендіру моделді жеңілдету мақсатында жасалынады. Динамикалық программалау моделі жеңілдетіледі, егер оны схема түрінде көрсетсек
сурет 7
. Әр қадам этапқа сәйкес келеді. Кері рекуррентті теңдеуін қолдана, әр қадамды i болатын жүйенің жағдайларын анықтайық. i, i+1, …, N этаптарындағы
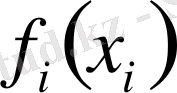 жалпы шығындардың минималды түрі болсын.
жалпы шығындардың минималды түрі болсын.
Реккурентті теңдеу түрі былай
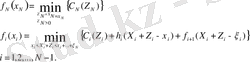
Тура реккурентті теңдеуді біз i қадамында жағдайлар немесе соңында қордың көлемін анықтай табамыз. Бұл жағдайлар
7-ші суретте
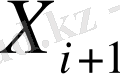 мөлшерімен берілген.
мөлшерімен берілген.
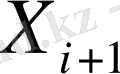 мәні кезкелген қадамда келесі шектеулерге тіреледі:
мәні кезкелген қадамда келесі шектеулерге тіреледі:
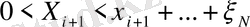
Сонымен шекті жағдайында
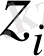 заказдалған өнімнің көлемі i этапында аса үлкен болуы мүмкін, сондықтан
заказдалған өнімнің көлемі i этапында аса үлкен болуы мүмкін, сондықтан
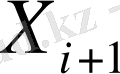 қоры барлық этаптағы сұранысты қанағаттандырады.
қоры барлық этаптағы сұранысты қанағаттандырады.
Тұрақты және кемімелі шекті шығындардың жеке жағдайы
Динамикалық программалаудағы моделді кез келген шығындар функциясында қолдануға болады. Моделдің негізгі жағдайы болатын этаптың бір мезетінде сақтау және сатып алу шығындарының тұрақты немесе кемімелі функция болуынан шығады. Бұндай жағдайда шекті шығындар тұрақты немесе кемиді. Шығындар функцияларының қарапайым түрлері 8-ші суретте көрсетілген. Математикалық тұрғыда бұндай функциялар дөңес болып келеді. Жағдай 1, тұрақты шекті шығындарға сәйкес келеді. Жағдай 2, көптеген шығындар функцияларына келеді өндірісте, өндіріске тәуелсіз заказды түзету шығындары К -ға тең. Бұл жағдайында шекті шығындар тең. Және соңғы жағдай 3, дөңес функциясының жалпы түрін көрсетеді.
Көрсетілген жағдайларға байланысты келесіні дәлелдеуге болады:
- Бастапқы берілгені бойынша қор деңгейі x1=0 N-этапты оптималды моделдер болып Zi оң мәнді немесе Xi* бастапқы қор оң мәнді; олардың туындысы нөлге тең болуы керек.
- Заказ мөлшері Zi кез келген i этапында нөлге тең немесе келесі этаптардың сұранысына сәйкес келгенде оптималды болады.
Бірінші жағдайдан шығатыны кез келген этапта бір уақытта қорды толтыру және заказды орналастыру рационалды емес. Минималды шекті шығындар сақтауға және сатып алуға бір бірлік өнім үшін бастапқы этаптағы қазіргі этапта b1 -ға тең болса, онда орналастыру шекті шығыны бір қосымша өнім жағдайында этаптың басында b11 - ға тең.
Егер b1<b11, онда заказ мөлшерін үлкейтуге болады.
Жоғарыдағы айтылып кеткен қасиеттер арқылы есептеу схемасын әлдеқайда жеңілдетеді. Оның негізін динамикалық программалау принциптері және алгоритмдері құрайды.
Өндірісті календарлы болжау N - этапты моделі
Өндірісті календарлы болжау N - этапты моделін қарастырайық. Сұраныс уақытқа байланысты өзгереді, бірақ детерминантты емес. Сұранысты қор деңгейін өзгерту арқылы, қор тұрақты болғанда өндіріс көлемін өзгерту арқылы, екеуінің өзгеруі арқылы да қанағаттандыруға болады. Өндіріс көлемін өзгерту қосымша жұмыс арқылы, ал қор деңгейін оң мәнді қорын ұстау арқылы немесе сұранысты қанағаттандырмайтын жағдайда болуы арқылы жүзеге асыруға болады. N -этапты өндірістің жалпы шығындарды минимизациялайтын календарлық жоспарын табу керек.
Моделде кез келген этапта түзету шығындарын нөлге теңестіреді. Жалпы айтқанда дефицит бар дейді, бірақ барлық қарыздар этаптардың соңында өтелуі тиіс. Бұндай берілгенін транспорттық есеп түрінде жазуға болады. Сонымен қатар егер дефицит жоқ болса, есепті оңай шығаруға болады.
Этаптарға байланысты келесі түсініктерді енгізейік:
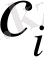 - жай күндердегі өндірістік шығындар;
- жай күндердегі өндірістік шығындар;
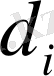 - қосымша жұмыс істеген күндердегі өндірістік шығындар;
- қосымша жұмыс істеген күндердегі өндірістік шығындар;
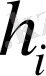 - этаптан этапқа көшіп жатқан сақтау шығындары;
- этаптан этапқа көшіп жатқан сақтау шығындары;
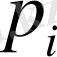 - дефициттен кеикен шығындар;
- дефициттен кеикен шығындар;
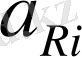 - өндірістік қуаттылық жай режимінде;
- өндірістік қуаттылық жай режимінде;
 - өндірістік қуаттылық қосымша уақытта;
- өндірістік қуаттылық қосымша уақытта;
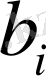 - сұраныс.
- сұраныс.
Айта кеткен жөн жай күндердегі өнімнің бағасы, қосымша уақыттағы өнімнің бағасынан кіші болады. Оны 9-шы суреттен көруге болады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz