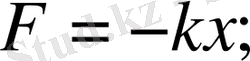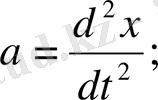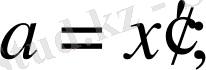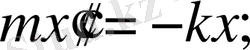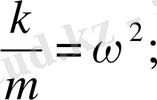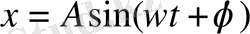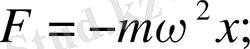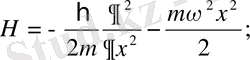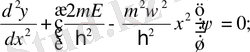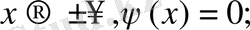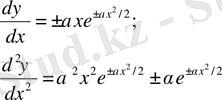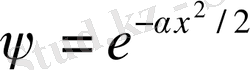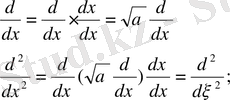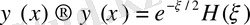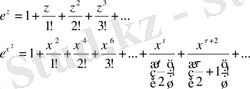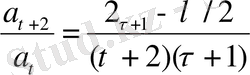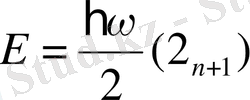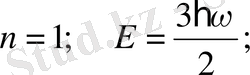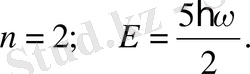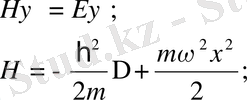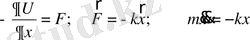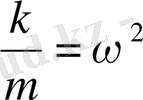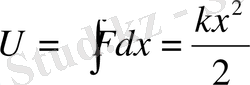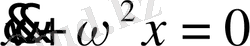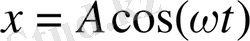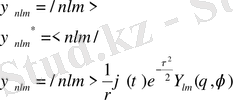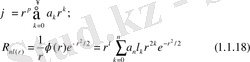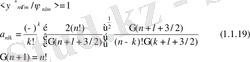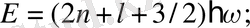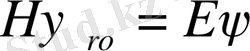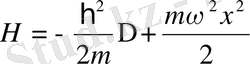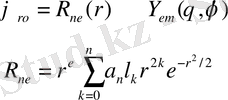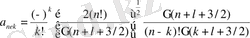Гармониялық осцилятор функциялары негізінде 58Zn және 58Ni ядроларының құрылымы мен толқындық функцияларын талдау


Мазмұны
- Кіріспе
ІІ. І-тарау. “Квант механикасындағы гармониялық
осцилатор” . . 4
- Гармониялық осцилатор 18
- Физикалық осцилатордың матрицалық элементтерін
гармониялық осцилатор функциялары арқылы табу.
ІІІ. ІІ-тарау. “Екі бөлшектік мәселе”. . 23
- Гармониялық екі
бөлшектің күйлері үшін трансформациялық
коэффициенттер
- Гармониялық осцилатордың толқындық функциясын кванттық туу операторы арқылы өрнектеу . 27
- Теорияны58Zn бен58Nі ядроларының құрылысын зерттеуге қолдану . . 32
Казахстан Республикасы Білім және ғылым министрлігі
ДИПЛОМДЫҚ ЖҰМЫС
Тақырыбы: “ 58 Zn бен 58 Nі ядроның құрылысын және олардың толқындық функциясын гармониялық осцилатор функциясы негізінде талдау”
Орындаған: Акбарова Э.,
4к. студенті, ФИ.
Ғылыми жетекшісі: профессор
Бақтыбаев Қырғызбай
Бақтыбайұлы.
Алматы 2002
Кіріспе
Осы дипломдық жұмыста гармониялық осцилатор функцияларының көмегімен атом ядросының құрылысын зерттеу мәселесі қаралған. Атом ядросының толқындық функцияларын осцилаторлық функциялар бойынша жіктеп шешу мәселені әлдеқайда оңайлатады.
Гармониялық осцилатор толқындық функциясы квант механикасында үлкен роль атқарады. Бұл квант механикалық мәселелердің ішінде дәл шешілетін аз ғана есептің бірі. Гармониялық осцилатордың симметриялық қасиеттері көптеген күрделі мәселелерді, әсіресе көп бөлшекті жүйелердің құрылысын зерттеуді әлдеқайда оңай, түсінікті түрге келтіруге себебін тигізді.
Сондықтан ядролық, атомдық және молекулалық физикада жүйенің толқындық функцияларын осцилаторлық функциялар бойынша жіктеп зерттеу жолдарын кейінгі кезде кеңінен қолдануда.
Өйткені Гамельтониан бөлшектер бойынша және кооррдинаттар бойынша бөлінгіштік қасиеті бар, сөйтіп оның әр түрлі координаттар жүйесінде аналитикалық шешулері бар. Сондықтан ядро теориясында жасалатын күрделі есептеулерді қолайлы және оңай түрге келтіреді.
Жұмыстың негізгі мақсаты:
а) Гармониялық осцилаторды қолданып көп бөлшекті мәселелерді қалай шешуге болатынын көрсету;
б) Ядролар үшін қолдану, оның ішінде жеңіл ядролардың спектрін есептеу болып табылады.
Осы мақсаттарды орындау үшін ең алдымен жұмыста гармониялық осцилатор функцияларын алудың квант механикалық жолы көрсетіледі. Сонан соң осы функциялардың көмегімен түрлі физикалық операторлардың матрицалық элементтерін есептеу жолы берілген.
Матрицалық элементтердің бүрыштық бөлімі барлық оператор үшін (сфералық координатта) ортақ. Оны есептеп шығару оңай. Сондықтан мәселе көбіне матрицалық элементтердің радиалды бөлігін есептеуге келіп тіреледі. Өйткені физикалық операторлар сфералық координаттар жүйесінде негізінде радиалдық бөлігімен ажыратылады.
Жұмыста одан әрі бір бөлшектік гармониялық осцилатор толқындық функцияларын кванттардың туу және жойылу операторлары арқылы өрнектеу жолы көрсетіледі. Тек осы жолмен ғана көп бөлшекті мәселелерді шешу өте оңай түрге енетіні белгілі.
Осыған сай 2S-1d қабықшасында болатын ерекшеліктерді зерттеу үшін қос түйық қабықша сыртында екі ғана нуклоны бар 58 Nі ядролары, 58 Zn ядролары қарастырылады. Бұл жерде біз тек осы ядролардың спектрлерін ғана есептедік. Бұл ядролардың ең төменгі энергетикалық спектрі осы осцилаторлық жуықтаумен жап-жақсы түсіндіруге болатынын көрсеттік.
1-тарау
Квант механикасындағы
гармоникалық осцилатор .
- Гармониялық осцилатор.
Гармониялық осцилатор дегеніміз не? Кәдімгі серпімділік күштердің әсерінен қозғалатын материалдық нүктенің барлығын гармониялық осцилатор ретінде қарастыруға болады. Қарапайым мысал ретінде жіпке ілінген математикалық маятникті алуға болар еді. Оның тербелесі гармониялық осцилатор болып табылады. Классикалық физикада гармониялық осцилатордың қозғалысы Ньютонның дифференциалды теңдеуіне бағынады. Оны былай жазуға болады:
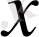 - дененің тепе-теңдік қалыптан ауытқуы;
- дененің тепе-теңдік қалыптан ауытқуы;
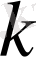 - коэффициент.
- коэффициент.
Енді осы Ньютонның дифференциалды теңдеуін мына түрде жазайық:
Equation. 3 (1. 1. 1)
 -қарастырып отырған дененің үдеуі.
-қарастырып отырған дененің үдеуі.
 үдеуіміз ауытқудың уақыт бойынша алынған екінші туындысына тең, яғни мынаған:
үдеуіміз ауытқудың уақыт бойынша алынған екінші туындысына тең, яғни мынаған:
Осы туынды алып отырған шаманы
 -деп қысқаша былай белгілейік:
-деп қысқаша былай белгілейік:
Енді осы
 - ты (1. 1. 1) теңдеуіне апарып қоямыз. Сонда:
- ты (1. 1. 1) теңдеуіне апарып қоямыз. Сонда:
 - дененің массасы .
- дененің массасы .
Осы теңдіктен
 - ты табатын болсақ, ол мынаған тең болады:
- ты табатын болсақ, ол мынаған тең болады:
(1. 1. 2)
Теңдеудегі
 мен
мен
 оң шама болғандықтан, олардың қатнасын
оң шама болғандықтан, олардың қатнасын
 деп белгілеп алайық. Яғни:
деп белгілеп алайық. Яғни:
 - тербеліс жиілігі.
- тербеліс жиілігі.
Сонымен (1. 1. 2) теңдеуіміз мына түрге келеді:
(1. 1. 3)
Біздің ендігі міндетіміз дененің қозғалысын анықтау болады. Бұл жөнінде бізге мыналар белгілі: дененің үдеуі (1. 1. 3) теңдеу бойынша, тепе-теңдік қалыптан х ауытқуына пропорционал және ол тепе-теңдік қалыпқа қарай бағытталған. Егер дененің орны уақыттың функциясы ретінде мәлім болса, онда дененің қозғалысы да белгілі болады. Бүл жағдайда
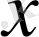 ауытқуды
ауытқуды
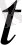 ауытқудың функциясы ретінде анықтау керек. Сонымен (1. 1. 3) теңдеуін қанағаттандыра алатындай
ауытқудың функциясы ретінде анықтау керек. Сонымен (1. 1. 3) теңдеуін қанағаттандыра алатындай
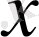 пен
пен
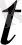 -ның арасындағы байланысты табуымыз керек. Бүл байланысты төмендегі теңдеу арқылы жазуымызға болады.
-ның арасындағы байланысты табуымыз керек. Бүл байланысты төмендегі теңдеу арқылы жазуымызға болады.
Яғни:
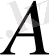 - амплетуда;
- амплетуда;
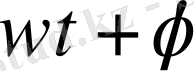 - фаза;
- фаза;
 - бастапқы фаза.
- бастапқы фаза.
Ньютонның негізгі дифференциалды теңдеуін жазамыз:
Ал, енді осы бір өлшемді гармониялық осцилатордың қасиеттерін кванттық физикада қарастырайық. Кез-келген гармониялық тербеліске келетін құбылыстардың барлығын
гармониялық осцилатор деп атаймыз. Осы қозғалыс үшін Шредингер теңдеуінің стационар түрін жазайық:
Бүл жердегі Гамильтонянымыз мынаған тең:
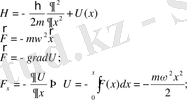
Осыдан Гамильтон операторының негізгі теңдеуін жазатын болсақ, ол мынаған тең болады:
Олай болса:
Мұндағы
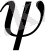 функциясы мына шегаралық шарттарды қанағаттандыруы керек:
функциясы мына шегаралық шарттарды қанағаттандыруы керек:
Енді мынадай белгілеулер енгіземіз:
(1. 1. 4)
Сонда:
(1. 1. 5) .
Осы теңдеуді шешейік. Ол үшін теңдеуді интегралдаймыз. (1. 1. 5) теңдеуді интегралдау үшін алдымен мынадай шектік жағдайды қарастырып алуымыз керек: х өте үлкен болғанда
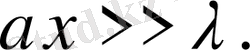
Онда (1. 1. 5) теңдеудің
 -ны
-ны
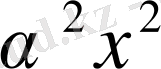 -пен салыстарғанда аз шама деп қарастырып, осы бөлікті ескермесек те болады.
-пен салыстарғанда аз шама деп қарастырып, осы бөлікті ескермесек те болады.
(1. 1. 6)
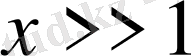 болғанда бүл теңдеудің шешімін жеткілікті дәлдікпен мына түрде беруге болады:
болғанда бүл теңдеудің шешімін жеткілікті дәлдікпен мына түрде беруге болады:
(1. 1. 7)
Шын мәнінде, ол мына түрде болады:
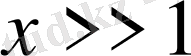 жағдайда соңғы теңдіктің оң жағындағы екінші мүшесі біріншімен салыстырғанда аз шама, сондықтан (1. 1. 6) теңдеудің шешімі (1. 1. 7) бола алады. Мүмкін екі таңбаның осы жағдайы үшін теріс таңбасын алады.
жағдайда соңғы теңдіктің оң жағындағы екінші мүшесі біріншімен салыстырғанда аз шама, сондықтан (1. 1. 6) теңдеудің шешімі (1. 1. 7) бола алады. Мүмкін екі таңбаның осы жағдайы үшін теріс таңбасын алады.
Себебі оң таңбалы шешім
 , шексіз өсе береді, ол бұл
, шексіз өсе береді, ол бұл
 функцияның шарттарын қанағаттандырмайды. Қарастырылған шектік жағдайды ескере отырып шешімді мына түрде іздейміз:
функцияның шарттарын қанағаттандырмайды. Қарастырылған шектік жағдайды ескере отырып шешімді мына түрде іздейміз:
(1. 1. 8)
мұндағы
 (1. 1. 8) теңдеуінің шешімі (1. 1. 6) теңдеуін қанағаттандыратын белгісіз функция түрінде алынады.
(1. 1. 8) теңдеуінің шешімі (1. 1. 6) теңдеуін қанағаттандыратын белгісіз функция түрінде алынады.
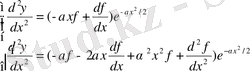
(1. 1. 9)
(1. 1. 9) -ды (1. 1. 5) -ке қоямыз
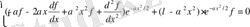
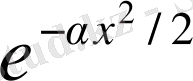 -ге қысқартып, теңдеуді мына түрге келтіреміз:
-ге қысқартып, теңдеуді мына түрге келтіреміз:
(1. 1. 10)
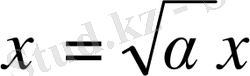 белгілеуін енгіземіз. Мындағы
белгілеуін енгіземіз. Мындағы
 өлшемсіз сан, ал
өлшемсіз сан, ал
 Equation. 3 -ның өлшемі [см
-2
] .
Equation. 3 -ның өлшемі [см
-2
] .
(1. 1. 10) теңдеуін
 -ға қысқартып, айнымалысын өзгерткеннен соң мына түрге енеді:
-ға қысқартып, айнымалысын өзгерткеннен соң мына түрге енеді:
(1. 1. 11)
Бұл Чебышев-Эрмит теңдеуі деп аталады.
Егер
 онда
онда
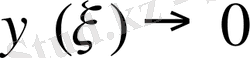
онда
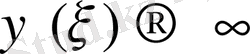
(1. 1. 12)
 -кіші мәндерінде ғана қатар жинақталады. Ол үшін қатардың алдындағы коэффициенттерін табуымыз керек.
-кіші мәндерінде ғана қатар жинақталады. Ол үшін қатардың алдындағы коэффициенттерін табуымыз керек.
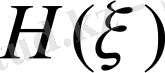 -дің туындыларын табайық.
-дің туындыларын табайық.
Сонда:
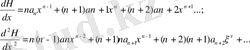
Осы туындыларды (1. 1. 11) теңдеуге қоямыз:
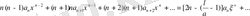 Екі қатардың тең дәрежелі мүшелері бір-біріне тең болуы керек, яғни олардың алдындағы коэффициенттері тең болуы керек. Сол жақ қатардың ең төменгі дәрежелі мүшесі
Екі қатардың тең дәрежелі мүшелері бір-біріне тең болуы керек, яғни олардың алдындағы коэффициенттері тең болуы керек. Сол жақ қатардың ең төменгі дәрежелі мүшесі
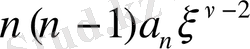 . Оның коэффициенті нөлге тең, себебі оң жақтағы қатарда мұндай дәрежелі мүше жоқ.
. Оның коэффициенті нөлге тең, себебі оң жақтағы қатарда мұндай дәрежелі мүше жоқ.
1)
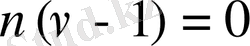 Equation. 3
Equation. 3
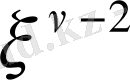 Equation. 3 дәрежелі мүше коэффициенті.
Equation. 3 дәрежелі мүше коэффициенті.
2)
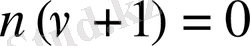 Equation. 3
Equation. 3
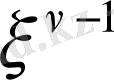 Equation. 3 дәрежелі мүше коэффициенті.
Equation. 3 дәрежелі мүше коэффициенті.
Осыдан:
 болуы мүмкін емес, себебі мүшесі
болуы мүмкін емес, себебі мүшесі
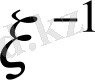 деп басталатын қатар
деп басталатын қатар
 болғанда
болғанда
 -ке айналып кетеді.
-ке айналып кетеді.
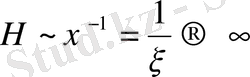
 -дің екі мәнді болуына байланысты
-дің екі мәнді болуына байланысты
 қатар екіге жіктеледі:
қатар екіге жіктеледі:
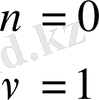 болғанда
болғанда
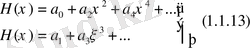
(1. 1. 14)
Бұл формула қатардың барлық мүшесін белгілі-бір мүшесі арқылы тізбектеп шешу мүмкіндігін береді. (1. 1. 13) теңдеуіндегі қатарлар (1. 1. 11) теңдеуінің дербес шешімдері бола алады.
(1. 1. 14) -теңдеу рекуренттік теңдеу деп аталады.
Енді алынған қатардың
 -дің үлкен мәндеріндегі жағдайларын қарастырамыз. Кез-келгенін алсақ (мысалы 1-шісін), оның
-дің үлкен мәндеріндегі жағдайларын қарастырамыз. Кез-келгенін алсақ (мысалы 1-шісін), оның
 -дің үлкен мәніде
-дің үлкен мәніде
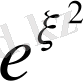 функциясына ұқсас болатынын көреміз.
функциясына ұқсас болатынын көреміз.
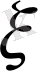 -дің жеткілікті үлкен мәндерінде қатардың бірінші мүшелерінің мағынасы аз.
-дің жеткілікті үлкен мәндерінде қатардың бірінші мүшелерінің мағынасы аз.
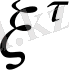 және
және
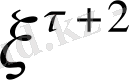 -ді,
-ді,
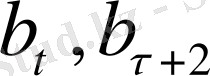 деп белгілеп қатынасын алсақ:
деп белгілеп қатынасын алсақ:
(1. 1. 15)
Оларға сәйкес қатар мүшелерінің қатынасы мына түрге енеді:
жеткілікті үлкен
 үшін
үшін
(1. 1. 16)
(1. 1. 15) пен (1. 1. 16) -ны салыстыра отырып мынадай қорытындыға келеміз:
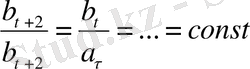
яғни біздің қатардың жоғарғы мүшелері
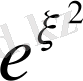 қатарының жоғарғы мүшелерінен айырмашылығы тұрақты көбейт-кішінің болатындығында. Бұл
қатарының жоғарғы мүшелерінен айырмашылығы тұрақты көбейт-кішінің болатындығында. Бұл
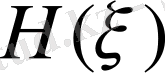 -дің де үлкен
-дің де үлкен
 - үшін
- үшін
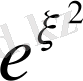 сияқты өсетіндігін көрсетеді.
сияқты өсетіндігін көрсетеді.
Олай болса:
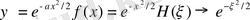
яғни
 функциясы
функциясы
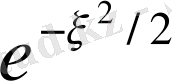 түрде болады
түрде болады
.
Егер қатар белгілі-бір мүшесінде үзілсе, онда ол қатар шекті қатар деп аталады. Оны полином деп атаймыз. Оны үзетін мәнді, яғни полиномның үзілу мүшесін (1. 1. 14) теңдеуден табамыз.
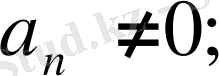
болса, онда
болады.
Осы полиномды Эрмит полиномы деп атаймыз.
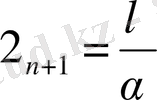 орындалу міндеті
орындалу міндеті
(1. 1. 17)
 функция осцилатордың толқындық теңдеуінің шешімі ғана болып қоймай, осцилатор энергиясының дискреттік мәндеріне ғана сәйкес шектік шарттардың да шешімі болады. (1. 1. 17) теңдеуі ескі квант теориясындағы
функция осцилатордың толқындық теңдеуінің шешімі ғана болып қоймай, осцилатор энергиясының дискреттік мәндеріне ғана сәйкес шектік шарттардың да шешімі болады. (1. 1. 17) теңдеуі ескі квант теориясындағы
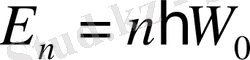
формуласына өзгереді.
(1. 1. 17) теңдеуіне сәйкес сызықты осцилатордың кванттық саны “жартылай сан” n+1 сипатталады.
Шредингердің толқындық функциясын табу жолында энергияның, яғни
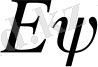 -дің өздік мәнін таптық.
-дің өздік мәнін таптық.
Ол осцилатордың энергиясы деп аталады.
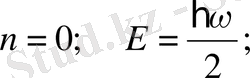
Бөлшек арақашықтығы
 Equation. 3 -дан тұратын бір-біріне тең ара қашықтықта ғана орындалады. Басқаша айтқанда - энергия кванты. Бұнда энергия дискретті ғана мәндер алады. Энергияның арасындағы мәндерді қабылдамайды. Осцилатордың ең кіші мәні n=0 болған кезде болады. Ал классикалық физикада х=0 болса, онда E=0 болады.
Equation. 3 -дан тұратын бір-біріне тең ара қашықтықта ғана орындалады. Басқаша айтқанда - энергия кванты. Бұнда энергия дискретті ғана мәндер алады. Энергияның арасындағы мәндерді қабылдамайды. Осцилатордың ең кіші мәні n=0 болған кезде болады. Ал классикалық физикада х=0 болса, онда E=0 болады.
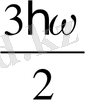
Қозғалысты толық жойып жіберуге болмайды. Квант механикасы сол диалектикаға классикалық физикамен әлдеқайда жақын. Сонымен, біз энергияны алдық. Енді толқындық функцияның кәдімгі аналитикалық түрін жазайық. Ол үшін полином n-ші мүшеге дейін:

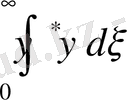 Equation. 3 нормалау шарты осыдан а
n
-ді табамыз.
Equation. 3 нормалау шарты осыдан а
n
-ді табамыз.
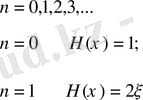
Толқындық функцияның ең төменгі деңгейіндегі толқындық функциясы Гаусс функциясына тең болады.
n=1 болғанда ості үш жерде қиып өтеді.
n=1 болғанда ості үшке қиады. Енді қайта Шрейдингер теңдеуін жазайық.
Мұны сфералық функцияда шешкеніміз оңай.
Ол Шар функциясы бойынша жазылады.
Осыдан а-ны тауып, есептей келе:
ал энергиясы:
Шредингер теңдеуі:
Гамильтон мынаған тең болады:
х-ығысу шамасы.
Бұл жердегі:
Кез келген күрделі басқа системаның толқындық функциясын әр уақытта осы қатармен жіктеуге болады.
1. 2. Физикалық операторлардың матрицалық элементтерін гармониялық осцилатор функциялары арқылы табу.
Егер бізге ортагональды, нормоланған, толығымен белгілі толық функцияның физикалық операторының матрицалық элементтері берілсе, кез-келген кванттық функцияны осы гармониялық осцилатор функциялары арқылы жіктеуге болады. Бұлай жіктеу әдісі есепті шешу жолын толық сипаттап береді. Жіктеу себебі: кванттық теорияда дененің күйін сипаттау барысында тербелістер өте күрделі болады, толқындық функцияларын шешу қиындайды, барлық мәндері өзгеріп отыруы жиі кездеседі. Осындай толқындық функциялары бар физикалық оператордың матрицалық элементін гармониялық тербелестің жиынтығы ретінде қарастыруға болады.
Гармониялық тербелесті сипаттайтын функцияның негізгі теңдеуін жазайық:
... жалғасы
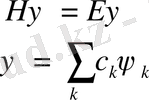
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz