Өндіріс және шығындар

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 74 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

М. Өтемісов атындағы Батыс-Қазақстан мемлекеттік университеті

Экономикадағы ақпараттық технологиялар кафедрасы

ДИПЛОМДЫҚ ЖҰМЫС

«Кәсіпорындағы ЭАЖ жобалау кезінде математикалық аппараттарды қолдану»

Орал, 2007 ж.

МАЗМҰНЫ

Кіріспе3

Ι бөлім. «Шығарылым-шығындар» жүйесінің экономикалық сипаттамасы6

1. 1 Өндіріс және шығындар6

1. 2 Қысқа мерзімді шығындар. Жиынтық, орташа және шектік шығындар20

1. 3 Ұзақмерзімді өндірістің шығындары31

ΙΙ бөлім. Модельдеу мен талдаудың математикалық әдістері35

2. 1 Өндірістік функциялар35

2. 2 Қосынды, орташа және шекті табыс және шығындардың функциялары45

2. 3 Өндірістік функцияны параметрлеу. Корреляциялық регрессиялық талдау48

III бөлім. «Завод металлоизделий» АҚ «шығарылым-шығындар» жүйесін модельдеу58

3. 1 Өндірістік функцияны параметрлеу және верификациялау58

3. 2 Шығындар функциялары71

3. 3 «Шығарылым-шығындар» ақпараттық жүйесінің интерфейсы және функциялары77

Қорытынды87

Қолданылған әдебиеттер91

КІРІСПЕ

Қазақстан экономикасы нарықтық қатынастарға өтуіне байланысты үлкен өзгертулер байқалды. Осы өзгертулер экономиканың негізгі буындар - кәсіпорындарға әсерін тигізді. ҚР үкіметінің жүзеге асырылған шараларының біріншілері меншік формаларының әр түрлілігін жариялау, кәсіпкерлік қызметтерінің еркіндігі болып табылды. Жоспарлы экономика жағдайында кәсіпорындарға белгілі шарттар жоғарыдан күшпен таңыған болса, ал нарықтық қатынастар жағдайында шаруашылық субъектілердің басты қағидалары қызметті таңдауда, шешімдерді қабылдауда, өзін-өзі қаржыландыруда еркін болды. Басты мақсаты - пайданы барынша көбейту, пайдалылықтың жоғары деңгейіне жету үшін кәсіпорындар «нені, қалай және қанша шығаруды» өз бетімен шешеді. Осы сұрақтарды дұрыс шешудің қажеттілігі осы тақырыптың қазіргі уақытта өзектілігін көрсетеді.

Экономикалық математикалық модельдеуді және экономикалық ақпараттық жүйелерді қолдану өте маңызды болып табылады, біріншіден ол экономикалық айнымалы шамалар мен объектілердің қатынастарын белгілеу және оларды формальды сипаттауға мүмкіндік береді. Екіншіден, дедукция әдістермен нақты құрастырылған алғашқы деректер мен қатынастардан зерттелген объектілер бойынша адекватты қорытындыларды алуға болады. Үшіншіден, математика және статистика әдістері индуктивтік жолымен объект туралы жаңа мәліметтерді алуға мүмкіндік береді: оның қадағалауларына сәйкес келетін айнымалы шамалардың тәуелділік формасын және параметрлерін бағалау. Және төртіншіден, математика тілі экономикалық теориясының ережелері, түсініктері мен қорытындыларды дәл және жинақы түрінде сипаттауға мүмкіндік береді.

Осы жұмыстың мәні, ең алдымен, экономикалық жүйелердің қызмет ету теориясының, математикалық модельдеу әдісінің, экономикалық ақпаратты жүйелеу мен өңдеу тәсілдерінің бірігуінен тұрады. Экономикалық математикалық модельдеудің өнімі және пәні өндіріс факторлары мен шығарылатын өнім көлемдерінің өзара байланысын сипаттайтын өндірістік функциялар мен шығындар функциялары болып табылады. Және сонымен бірге белгілі уақытта экономикалық жүйенің жағдайын зерттеуге және оның мүмкін болатын жағдайларын құрастыруға мүмкіндік беретін математикалық моделі болады.

Экономикалық теорияда «шығарылым-шығындар» жүйесін талдаудың негізін салушылары Леонтьевтің экономиканың салааралық балансы, Кобба-Дуглас өндірістік функциясы және басқа да ғылыми енбектер болды. Модельдеудің математикалық негізін қазіргі экономиканың әртүрлі аппараттары құрайды: функционалдық тәуелділікті құрастыру мен бағалаудың эконометриялық әдістері, дифференциалдық санау әдістері, сызықтық және сызықтық емес теңдеулер жүйелері. Графикалық сипаттамасы Microsoft Excel бағдарламасы көмегімен берілді. Қорыта келгенде, модельдерде құрастыру және қолдану ақпаратты жинақтау және стандарттау бойынша көп жұмысты қажет етеді. Сонымен, «шығарылым-шығындар» жүйесін модельдеу - бұл экономикалық ғылымда синтетикалық бағыт.

Дипломдық жұмыстың мақсаты «шығарылым-шығындар» жүйесінің экономикалық математикалық моделін құрастыру болып табылады. Осыдан шығып, өз алдыма мынадай міндеттерді қоямын:

өндірістік шығындарды зерттеу, олардың шығырылатын өнім көлеміне қатынасы.
Математикалық аппаратты дайындау.
Объектінің ішкі және сыртқы ұйымдастыру ортасын сипаттау.
Өндірістік функциясы мен шығындар функциясын құрастыру, графикалық талдау.

Жұмыстың объектісі «Завод металлоизделий» АҚ болып табылады, ол 1929 ж. бастап қызмет етеді және бірінші онжылдықта сүт құрал-жабдықтарды (электросепараторлар) және халық тұтынатын тауарларды шығарды. Дипломдық жұмыстың ақпараттық жүйесін дайындау практикалық бөлімінің негізінде кәсіпорын қызметінің сол кезеңінің мәліметтері алынған.

Дипломдық жұмыс кіріспе, үш бөлім, қорытынды және пайдалынған әдебиеттер тізімінен тұрады.

Бірінші бөлімінде «Шығарылым-шығындар» жүйесінің экономикалық сипаттамасы», онда өндіріс шығындар, шығындар функциялары және өндірістік функцияларына анықтамалар берілген, және сонымен бірге олардың өзара қатынасы сипатталған. Сондай-ақ шығындар қисығы және әр түрлі уақыт интервалдарында олардың тәртіптері сипатталған.

Екінші бөлімінде «Модельдеу мен талдаудың математикалық әдістері» зерттелетін көрсеткіштер арасындағы функционалды тәуелділіктерді анықтаудың негізгі математикалық әдістері қарастырылған, соның ішінде өндірістік функциялар, шығындар функциялар құрастырылған және оларға талдау жүргізілген.

«Завод Металлоизделий» АҚ «шығарылым-шығындар» жүйесін модельдеу» үшінші бөлімінде - кәсіпорын мысалында «шығарылым-шығындар» принціпінің практикалық жүзеге асырылуы көрсетілген. Мұнда мен бірнеше өндірістік функциялар мен шығындар функцияларын өз бетімен құрастыра отырып және олардың салыстырмалы талдауын өткіздім.

Ι бөлім. «Шығарылым-шығындар» жүйесінің экономикалық сипаттамасы

1. 1 Өндіріс және шығындар

Әрбір шешімнің альтернативтік құндылығы - ол басқа шамалы шешімдердің ішіндегі ең жақсысы. Ресурстарды қолданудың альтернативті шығындары - бұл пайдаланудың басқа шамалы альтернативтік нұсқалардың ішіндегі ең жақсы нұсқада пайдалынатын ресурстардың бағасы. Кәсіпкер өз кәсіпорының басқаруға кететін жұмыс уақыттын альтернативті бағасы - ол өз жұмыс күшін басқа кәсіпорынға сатпай, бас тартқан жалақысы немесе кәсіпкердің бас тартқан бос уақыттың бағасы - осы екеуіннің ішіндегі артығына байланысты.

Кәсіпорынға жұмсалған қаражаттардың альтернативтік бағасы, егер бұл қаражат басқа өндіріске жұмсалған болса, осы қаражаттан түсетін пайдасының мүмкіндігінше көп пайдасымен анықталады.

Есепшілер анықтайтын шығындардың ішіне, кәсіпорын иелерінің жеке меншігі болып табылатын, өндіріс факторларының альтернативті бағасын қоспайды. Кәсіпорын иелері бухгалтерлік шығындардың толықеместігін түсінеді және өз шешімдерінде альтернативті шығындарға сүйенеді. Кәсіпорынның альтернативті шығындары экономикалық шығындар деп аталады.

Тауар өндірісінің экономикалық шығындары қолданылатын ресурс санына және өндіріс факторлар қызметінің бағасына тәуелді. Егер кәсіпкер сатып алынбайтын, өз ресурстарын қолданатын болса, бағалар шығындар шамасын дәл анықтайтын бірдей өлшем бірліктерде көрсетілу тиіс.

Шығындар функциясы өнім шығарылымы және оған кететін минимальдық мүмкін бола алатын шығындардың арасындағы қатынасты сипаттайды. Өндірістік ресурстардың технологиясы мен бағалары, әдетте, шығындар функциясын анықтау кезде деректер ретінде алынады. Қандай да бір ресурс бағаларының өзгерісі немесе жаңа жақсартылған технологияны қолдану сондай көлемде шығарылытын өнімнің минимальдық шығындар көлеміне әсер тигізеді.

Барлық кәсіпорындар тиімді өндіруші болуға ұмтылады. Бұл мақсатқа жету үшін кәсіпорын өндіріс әдістерінің ішінен технологиялық және экономикалық жағынан тиімді әдістерді қолдану керек.

Белгілі көлемде өнім өндірісінің ресурстардың ең болмаса бір түрінің аз мөлшері жұмсалатын, ал басқа түрлері одан арттығырақ жұмсалмайтын өндірістің басқа әдісі болмаса бұл өндіріс әдісі технологиялық тиімді болып табылады. Немесе, егер өндірілген өнім көлемі дәл анықталған ресурстар көлемін пайдалағанда максимальды мүмкін болатын болса, өндіріс әдісі технологиялық тиімді болады

Қандай да бір өнім көлемін шығаруда экономикалық тиімді әдіс - ол өндіріс үрдісінде қолданылатын шығындар түрлерінің альтернативтік құнын минимизациялайтын әдіс.

Өндірушілер минимальды шығындарды қолдана отырып өнімді шығара алмаса, тиімсіз өндіріс орын алады. Өндіріс факторларын қолдану нұсқаларының ішінен шығарылатын өнім көлемін қысқартпай, шығындарды төмендетуге мүмкіндік беретін нұсқа таңдап алынады. Басқа жағынан қарағанда, шығындарды көбейтпей, сол ресурстар жиынтығы кезінде шығаратын өнім көлемін ұлғайту өндірушіге қолайлы болып табылады

Шығындар функциясы өндіріс функциясымен байланысты. Берілген комбинация факторында қандай да бір өнім көлемін шығарғанда шығындарды минимимизациялау максимальды мүмкін бола алатын өндіріс көлемін шығаруына байланысты.

Изокостілер

Тек қана айнымалы 2 фактор - еңбек және капитал қолданылады деп ұйғарайық, және бұл факторлардың тұтыну құны сәйкесінше Р ₁ және Р _k . Осы екі факторлардың қандай да бір саның қолданудың жиынтық шығындар (ТС) :

ТС=Р _l L+Р _k К, (1. 1)

құрайды, мұнда L еңбек сағаттарында, ал К машина жұмысының сағаттарында өлшенеді; Р _l - сағаттап жұмыс ақысы; Р _k - машиналар үшін сағаттап жалгерлік төлемнің шамасы.

Изокостілер - өндіріс шығындар тең болғанда еңбек және капитал шығындардың байланысын көрсететін, сызық. Мысалы жұмыс қызметінің бағасы (еңбек ақы) сағатына 10 долл., ал капитал қызметінің бағасы (машина жұмысының жалгерлік төлемі) сағатына 20 долл. деп ұйғарайық. Жұмыстың 500 сағатын және машиналар жұмысының 250 сағатын қолданғанда шығындар бір айда 1 долл. құрайды. Графикте осы факторлардың комбинациясына сәйкес келетін нүктелер сәйкесінше А және В деп белгіленген (1. 1 сурет, А) . Шығындар айына 1 долл. құрайтын, әрбір басқа факторлардың комбинациясына изокостідегі А және В нүктелерінен өтетін нүктеге сәйкес келеді.

(1. 1) теңдеуі еңбек пен капиталға берілген бағаларындағы изокостілер үйірін сипаттайды. Еңбек және капитал шығындардың әрбір деңгейінде өз изокостісі бар. Бұл графикте көрсетілген, онда түзу сызықтың әртүрлі ресурстық комбинациялар үшін шығындардың белгілі деңгейіне әрбір түзу сызық сәйкес келеді.

1. 1 сурет. Изокостілер

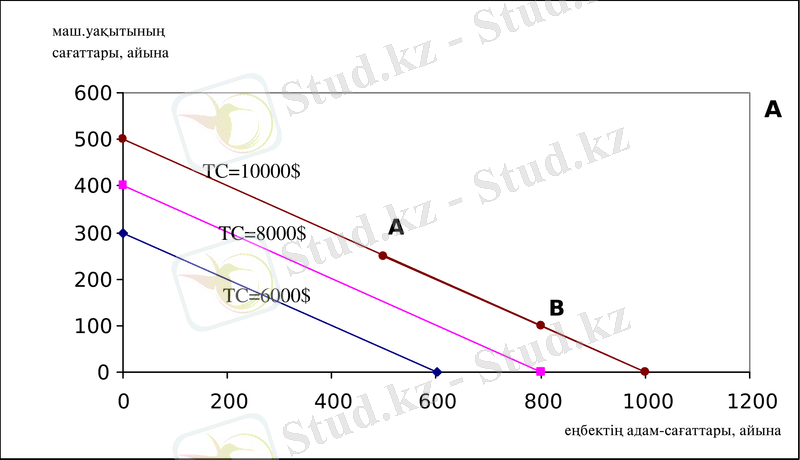
Егер еңбек бағасы сағатына 10 долл., капитал бағасы - сағатына 20 долл. болса, онда машиналар жұмысының әр сағатының қысқартылуы, жұмыстың тағы екі сағаты үшін төлеуге болатын, 20 долл. үнемдейді. Изокостілер үйірінің әр түзудің көлбеулігі ∆К/∆L тең. Еңбек шығындарының 1 сағатқа қысқартылуы есебінен капитал қолданудың мүмкін бола алатын көбеюі Р _l /Р _k тең.

Жұмсалатын факторлардың бағаларының қатынасы теріс таңбасымен алынған изокоста сызығының көлбеулігіне тең. Осыны растау үшін берілген изокоста сызығы үшін ТС тұрақты екенін еске түсіріңіздер. Қолданылған капитал санының ΔК-ға қысқартқанда жиынтық шығындардың шамасы - Р _k ΔК-ға төмендейді. Шығындардың жиынтық деңгейі тұрақты болу үшін, еңбектің Р _l ΔL қосымша сағаттарын төлеуге шығындардың көбеюі осы изокостіде қалатындай болып капиталдың қысқартылуын компенсациялау керек. Сонымен, осы изокоста үшін:

Р _l =-Р _k ΔК

осыдан шығады

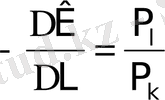
К үшін теңдеуді (1. 1) шешіп осыны көруге болады:

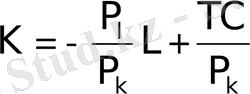(1. 3)

Осы жағдайда:

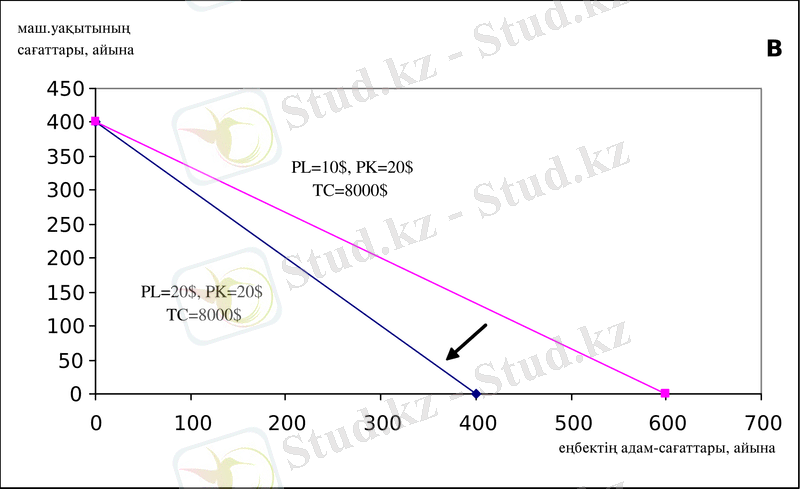
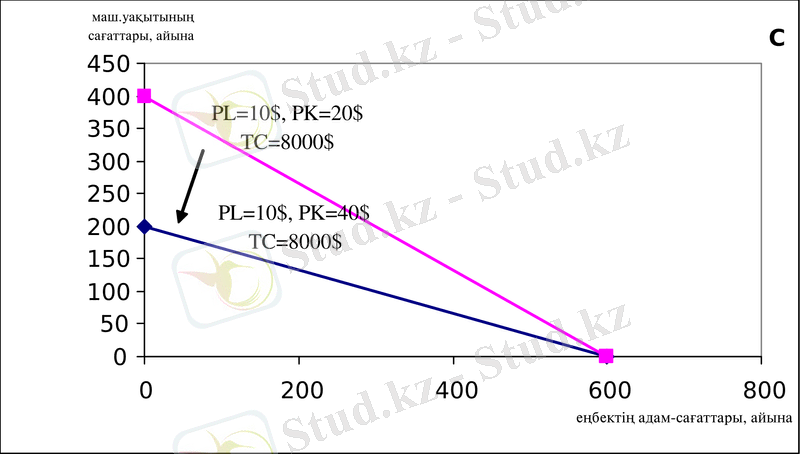
Осыдан, изокоста көлбеулігі -0. 5 тең. Жұмыс немесе капитал бағасының өзгерілуі изокостілер барлық үйірінің көлбеулігін өзгерту мүмкін. Мысалы, капитал бағасының тұрақтылығында жұмыс бағасының көбеюі осы үйірінің әрбір изокостасын тік етеді. В-графигі (1. 1 сурет) еңбек бағасының көбеюі капиталмен салыстырғанда үйірдің әрбір изокостасын тік ететінің көрсетеді. С-графигі (1. 1 сурет) берілген еңбек бағасының капитал бағасының көбеюі үйірдің әрбір изокостасын жайпақ етеді. Еңбек бағасымен салыстырғанда капитал бағасы көбейгенде де осылай болады. (І өсу қарқыны ІІ өсу қарқыннан артық болады) .

Өндірістік функциясы. Изокванта түсінігі

Өндіріс факторларының әрбір жиынтығы және осы факторлар жиынтығынан өндірілетін өнімнің максимальды мүмкін бола алатын көлемі арасындағы қатынасы өндірістік функциясымен сипатталады. Өндірістік функция берілген технология үшін құрастырылады. Технологияның жақсаруы, факторлардың әрбір комбинациясының өнім шығарудың барынша жетілетін көлемінің көбеюі жаңа өндірістік функциясымен көрсетіледі. Өндірістік функция түрлі тауардың берілген көлемін өндіру үшін қолданылуы мүмкін.

Егер өндіріс факторлары немесе ресурстар жиынтығын еңбек, материалдар және капитал шығындары ретінде көрсетсек, онда өндірістік функция былайша сипатталады:

Q=f (L, K, M) (1. 4)

мұнда осы технология және L-еңбектің, K-капиталдың және М-материалдардың берілген қатынасында өндірілетін өнімнің максимальдық көлемі - Q.

Өндірістік функция шығарылым көлемі және қолданылатын факторлар саны арасындағы қатынасын анықтайды.

1. Басқа да тең шарттарда бір ресурс шығының көбейту арқылы өндіріс көлемінің көбеюінің шегі болады. Бұл, мысалы, фабрикада станок және өндірістік бөлмелер белгілі бір мөлшерінде жұмысшылардың көп саның тарту арқылы өндіріс көбеюінің шегі бар екеннің болжайды. Жұмысшылар өсімі арқылы өндірістің өсімі нөльге жақындайды. Шыңында, фабрикадағы әрбір жаңа жұмысшы өнім шығарылымың өсуіне емес қысқаруына әсер ететін нүктеге жетуге болады. Егер жұмысшы жұмысқа қажетті құрал-жабдықпен қамталмаса, және ол өз қатынасуымен басқа жұмысшы еңбегіне кедергі келтірсе, осы орын алады.

2. Өндіріс факторларының белгілі өзара толықтыруы бар, бірақ өндіріс көлемін қысқартпай осы факторлардың белгілі бір бір-бірін ауыстыру мүмкіндігі бар. Егер жұмысшылар барлық қажетті құралдармен жабдықталса, онда олар өз жұмысын тиімдірек орындайды. Сондай-ақ, егер жұмысшылардың құралдарды қолдануға біліктіліктері болмаса, онда құралдар пайдасыз қалуы мүмкін. Бірақ, өндірісте бір ресурсты басқа ресурсқа ауыстыруға болады. Мысалы, жиһаздың белгілі саны мен сапасы жоғары механизацияланған әдіс немесе капиталдың аз мөлшері және еңбектің көп мөлшерін қолдануымен шығаруға болады.

Сонда да, өнімнің шығарылуын қысқартпай еңбектің қаншаға капиталға ауыстырылуының шегі бар. Және керсінше, қол еңбектің қолдануының шегі де бар. Бірақ машиналардың аз мөлшері мен жұмысшылардың көп санында машина жұмысының әрбір сағатын ауыстырыу үшін көп жұмыс сағаты керек.

3. Өндіріс факторлар қолдануының өзгеруі қысқа мерзімді уақытына қарағанда ұзақ мерзімде икемділеу. Мысалы, қысқа мерзімде өнеркәсіп өңдеу кәсіпорындар өз күштіліктерін арттыруға уақыт жетіспеулікпен және осы кәсіпорындар шегімен шектеулі.

Ұзақ мерзімді уақыт - бұл өндірушілер барлық өндіріс факторларын өзгертуге қажетті уақыт. Егер де өндірістің факторлары көбею мүмкін болса, онда өндіріс өсімнің шегі жоқ. Сәйкесінше, өндірушілер ұзақ мерзіміне қарағанда қысқа мерзімде қажетті өнімдерді өндіргенде көп қиындықтармен кездеседі.

Өндірістің маңызды аспектілері, мысалы, өндіріс факторлардың тек қана екі кең топтарын - еңбек пен капиталды қарастырған кезде, есепке алынуы мүмкін. Екі факторлық өндірістік функциясы арқылы өндірісті графикалық талдауға болады. Егер өндірістік функциясы өндірістің екіден көп факторды есепке алса, онда математикалық талдауды қолдану керек.

1. 1 кестеде жиһаз фабрикасында берілген технологиясында орындықтар шығару үшін қажетті еңбек және капитал шығындары арасындағы қатынасы туралы болжамды мәліметтер берілген. Осы мәліметтер жұмсалатын ресурстар және шығарылым көлемі арасындағы байланысында негізделген. Капитал шығындары бір ай ішінде машиналар жұмысының уақытымен анықталады, еңбек шығындары бір ай ішінде еңбек сағаттарымен өлшенеді. Машиналар жұмысының әр сағаты мен еңбек сағатының белгілі сапасы бар.

1. 1 кестеде бір сағат ішіндегі машина уақыты және еңбек шығындардың сәйкесінше әрбір комбинация үшін шығарылым көлемі туралы мәліметтері бар. Кестедегі мәліметтеріне сәйкес, әр ай сайын еңбектің 400 сағаты және машина уақытының 300 сағаты қолданылғанда, айына 250 орындық шығарылады.

Егер капитал көлемін координатаның вертикаль осінде, ал еңбекті координатаның горизонталь осі бойынша көрсетсек, онда өндірістік функциясы графикалық бейнелеуге болады (1. 2 суреті) . Жұмыс сағаттары және машина жұмысы сағаттарының әрбір комбинациясы графикте өндірістің немесе шығарылымның белгілі көлеміне сәйкес келеді. Мысалы, егер жұмыс уақытының 200 сағаты және машина жұмысының 400 сағаты қолданылса, онда айына 210 орындық шығарылады. Еңбек және капиталдың осы комбинациясына 1. 2 суретінің А нүктесі сәйкес келеді. Егер еңбектің 300 сағаты және машина жұмысының 300 сағаты қолданылса да айына орындықтың осындай да саны шығарылу мүмкін. Бұл қатынасты 1. 2 суретінде В нүктесімен белгілеуге болады. Д нүктесімен белгіленген, еңбектің 500 сағаты және машина жұмысының 200 сағатының комбинациясы осылай да айына 210 орындық шығаруға мүмкіндік береді.

1. 1 кесте. Өндіріс факторлар комбинацияларының кестесі:

бір айда орындық саны

Айына жұмыс уақыты, сағат

Айына машина-сағаттары

100

200

300

400

Айына жұмыс уақыты, сағат: 100

Айына машина-сағаттары: 20

Айына жұмыс уақыты, сағат: 200

Айына машина-сағаттары: 30

150

210

Айына жұмыс уақыты, сағат: 300

Айына машина-сағаттары: 55

150

210

270

Айына жұмыс уақыты, сағат: 400

Айына машина-сағаттары: 66

180

250

315

Айына жұмыс уақыты, сағат: 500

Айына машина-сағаттары: 72

210

270

320

Айына жұмыс уақыты, сағат: 600

Айына машина-сағаттары: 78

230

288

324

Айына жұмыс уақыты, сағат: 700

Айына машина-сағаттары: 83

245

305

327

Айына жұмыс уақыты, сағат: 800

Айына машина-сағаттары: 86

250

315

329

Алайда бұл өндірістік торда әдейі дәл көрсетілмеген, бірақ орындық өндірісі айына 210 болатындай еңбек және капитал комбинациясының басқа да нұсқаулары болуы мүмкін, ол графикте С нүктесімен белгіленген.

Изокванта - бұл белгілі өнім көлемін өндіруде ресурстар комбинациясының әртүрлі нұсқауларын көрсететін қисық. 1. 2 суретте изокванта бейнеленген, ол шығарылым көлемінің айына 210 орындыққа сәйкес келеді. Бұл қисықтың нүктелері шығарылымның максимальдық көлемі айына 210 орындыққа тең (берілген технология және өзгерілмейтін тең бағаларында) болғандағы еңбек және капитал шығындардың барлық комбинациясын көрсетеді.

Берілген өнім көлемін шығару үшін көптеген нұсқалар бар екенің осы изокванта көрсетеді. 1. 2 суретінде жоғары механизацияланған әдіс қолданылуы мүмкін, ол суретте А нүктесімен белгіленген. Керсінше, осыншама өнім мөлшері аз машина санымен және қол еңбектің көп мөлшерімен бір айда өндірілуі мүмкін. (графиктегі Д нүктесі)

1. 2 сурет. Изокванта

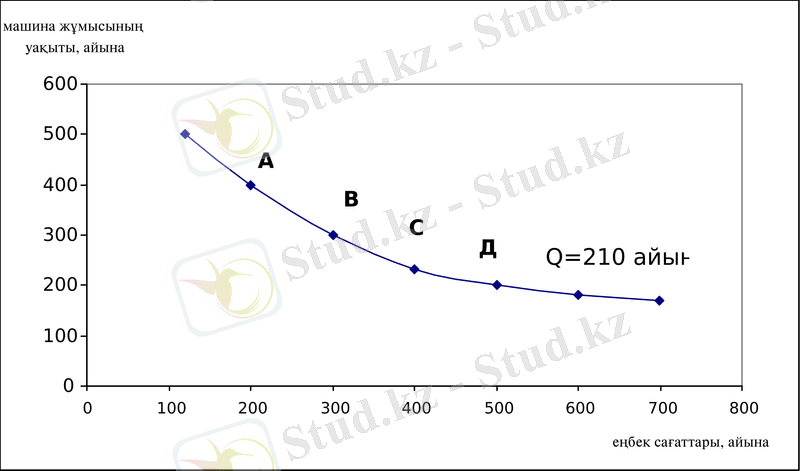
Осылайша изокванттар берілген өнім көлемін шығарғанда шығындардың альтернативтік нұсқаларын бейнелейді.

Шығындарды минимизациялайтын өндіріс факторларының комбинациясы

1. 3 суретте алдынғы изокванта көрсетілген. Изокосттар үйірі, сәйкесінше еңбек бағасы сағатына 10 доллар және капитал үшін жалгерлік төлемі сағатына 20 доллар, изокванта бейнеленген координаттар жүйесіне көшірілген.

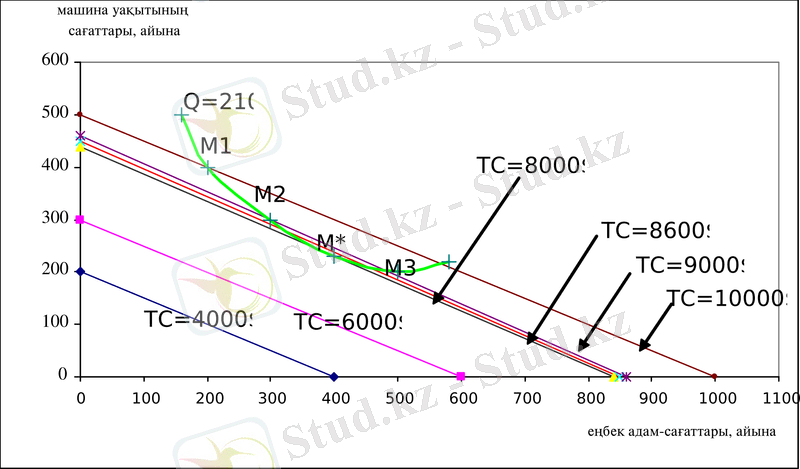
Өндіруші орындық шығарғанда шығындар функциясының қандай да бір нүктесіне өту үшін ресурстар комбинациясының қандай түрін таңдап алады? Шығындар функциясы шығарылатын өнім және өнімнің осы көлемін шығаруға қажетті минимальдық шығындар саны арасындағы байланысын көрсетеді. Орындық өндіруші, еңбек және капиталдың шығындардың осы комбинациясын қолдана отырып, шығарылым көлемі минимальдық шығындармен өндірілуіне сенімді болу керек. Мысалы, кәсіпорын қожайыны айына шығарылымы 210 орындыққа тең деп шешкен. Изоквантадағы М ₁ нүктесіндегі қолданылатын өндіріс әдісіне көз жүгіртейік. Бұл нүктеге еңбектің 200 сағаты және машина жұмысының 400 сағатының қолданылуы сәйкес келеді. Бұл әдісті қолданғанда өндіріс шығындары айына 1 долларды құрайды.

М ₂ әдісі өзіне еңбектің 300 сағаты мен машина жұмысының 200 сағатын қолданылуын қосады, ал шығындар тағы да 9000 доллар құрайды. М ₃ әдісі өзіне еңбектің 500 сағаты мен машина жұмысының тағы да 9000 долларын құрайды. М ₂ және М ₃ әдістері бір изоквантадағы нүктелерге сәйкес келеді, ол изокоста және изоквантаның жанасу нүктесі болып табылады. Бұл нүктеге сәйкесінше еңбектің 400 сағаты мен машина жұмысының 230 сағатын қолданылуы жатады. Жиынтық шығындар айына 8600 доллар құрайды. Осыдан өндірістің тепе-теңдік әдісі М* нүктесіндегі факторлар комбинациясына сәйкес келеді.

Белгілі шығарылым көлемін өндіруге кететін минимальдық шығындарын анықтау үшін екі түрлі ресурстардың изокванта көлбеулігі осы ресурстардың изокоста көлбеулігіне тең болу керек. Изокванта көлбеулігі теріс белгімен алынған капиталды еңбекпен технологиялық толтырудың шекті нормасына тең. Бюджет сызығының көлбеулігі теріс белгімен алынған еңбек бағасы мен капитал бағасының қатынасына тең. Осыдан шығар қорытынды:

MRTS _lk =P _l /P _k (1. 5)

Толтырудың технологиялық шекті нормасының шамасын еңбектің шекті өнімнің капиталдың шекті өніміне қатынасты деп алуға болады, онда:

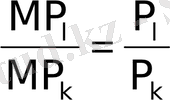(1. 6)

(1. 6) теңдігі минимальдық шығындармен өндірілетін берілген шығарылым көлемнің шартын анықтайды. Егер кәсіпорын шығарылатын өнім көлемін анықтай отырып, өзінің өндірісін өз шығындар функциясымен жүргіземіз деп ойласа, онда жоғарыда келтірілген шарт орындалу үшін кәсіпорын ресурстар комбинациясының қандай да бір нұсқасын таңдау керек.

(1. 6) теңдеуін былай жазуға болады:

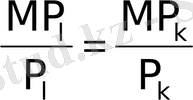(1. 7)

Бұдан шығар қорытынды мынадай: минимальдық шығындарымен берілген өнім көлемін өндіру бір уақытта қолданылатын ресурстар доллар шығындарына шекті өнімнің бірдей көлемін болуын талап етеді. Басқа сөзбен айтсақ, осы шарт орындала отырып, өндіруші берілген шығындар негізінде өнім шығарылымның максимальдық көлемін шығарады.

1. 3 суреті. Белгілі өнім көлемі өндірісіндегі шығындар минимизациясы