Есептерді нейрондық желілерімен баяндау

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 66 бет
Таңдаулыға:

МАЗМҰНЫ

1 ЖАСАНДЫ НЕЙРОНДЫҚ ЖЕЛІЛЕР14

1. 1 Нейрондық желілердің элементтері14

1. 2 Нейрондық желілердің сәулеті15

1. 3 Есептерді нейрондық желілерімен баяндау16

1. 4 Желіге кіріс сигналдарын беру және шығыс сигналдарын алу17

1. 5 Нейрондық желілерді оқыту18

1. 5. 1 Желінің жолдық параметрлері бойынша бағалау функциясының градиентін есептеу20

1. 5. 2 Нейрондық желі оқытуына әсер ететін факторлар22

1. 5. 3 Нейрондық желілерді жеңілдету23

1. 5. 4 Желі сигналдары мен көрсеткіштерін есептеу параметрлерінің маңыздылық көрсеткіштерін есептеу23

2 ЛОГИКАЛЫҚ МӨЛДІР НЕЙРОНДЫҚ ЖЕЛІЛЕР25

2. 1 Логикалық мөлдір нейрондық желілердің сәулеті26

2. 2 Нейрондық желі жеңілдету ережелері27

2. 3 Элементтердің бейсызықтығына қойылатын талаптар28

2. 4 Нейрондық желілерді логикалық мөлдір түрге келтіру30

2. 5 Нейрондық желілердің вербализациясы31

3 МӘЛІМЕТТЕР ҚҰРЫЛЫМЫН ӨҢДЕУ АЛГОРИТМДЕРІН ЗЕРТТЕУ ЖӘНЕ ҚҰРУ32

3. 1 Мәліметтердің файлдық құрылымы32

3. 1. 1 Кіріс және шығыс мәліметтері32

3. 2 Программаның объектілі-бағдарланған көрінісі33

3. 2. 1 Программа жұмыс істеуінің негізгі қадамдары35

3. 3 Программа сәулетін зерттеп жасау35

3. 3. 1 Объектілі-бағдарланған жобалау35

3. 3. 2 Кластар және объектілер37

3. 3. 3 Жүйенің программалық модульдерін жобалау38

3. 3. 4 Программалық модульдерде қолданылатын кластарды баяндау39

4 ПРОГРАММАНЫҢ СИПАТТАМАСЫ46

4. 1 Жалпы мәліметтер46

4. 2 Функционалдық арналуы46

4. 3 Логикалық құрылымның баяндалуы46

4. 4 Қолданылатын техникалық құралдар46

4. 5 Шақыру және жүктеу47

4. 6 Кіріс мәліметтері47

4. 7 Шығыс мәліметтері47

4. 8 Программаның хабарлары47

4. 8. 1 Программаның менюі47

4. 8. 2 Программаның құжаттарымен жұмыс істеудің жалпы принциптері48

4. 8. 3 Диалогтық терезелері50

4. 8. 4 Хабарлар50

5 ПРОГРАММАЛАУШЫНЫҢ АНЫҚТАМАСЫ52

5. 1 Жалпы мәліметтер52

5. 2 Программаның құрылымы52

5. 3 Программаның күйін келтіру53

5. 4 Программаны тексеру53

5. 5 Қосымша мүмкіндіктері53

5. 6 Программалаушыға хабар53

5. 6 Оператордың анықтамасы54

5. 6. 1 Программаның арналуы54

5. 6. 2 Программа орындалу шарттары54

5. 6. 3 Программаның орындалуы54

5. 6. 4 Операторға хабар54

6 КЕШЕНДІ ЕНДІРУДІҢ ЭКОНОМИКАЛЫҚ ТИІМДІЛІГІН ЕСЕПТЕУ55

6. 1 Программалық кешен зерттеп жасау қажеттілігін негіздеу55

6. 2 Программалық қамтама ендірудің экономикалық тиімділігін есептеу56

6. 2. 1 Жүйе зерттеп жасау мен ендіру шығындарын есептеу56

6. 2. 2 Жалақыға шығынды шығаруға арналған есептер58

6. 2. 3 Материалдарға жұмсалатын шығындар61

6. 2. 4 Ғылыми зерттеу жұмыстарына қажет арнайы аппараттарға кететін шығындар62

6. 2. 5 Басқа шығындар62

6. 3 Программалық қамтаманы енгізуінің тиімділігін есептеу63

6. 3. 1 Енгізуге дейін шығынды есептеу63

6. 3. 2 Көппараметрлі модель құру жүйесін енгізуден кейін шығынды есептеу64

6. 3. 3. Жүйенің өтеу мерзімі64

6. 3. 4 Жылдық экономикалық эффект65

7 Еңбек қорғау бөлімі65

7. 1 Жұмысшыға қауіптілік пен зияндылық төндіретін негізгі құрал-жабдықтарды талдау65

7. 2 Негізгі қорғау шаралары67

7. 2. 1 Жалпы ұйымдастыру шаралары67

7. 3 Өндірістік санитария68

7. 3. 1 Өндірістік микроклимат68

7. 3. 2 Психофизиологиялық факторлар69

7. 3. 3 Электромагниттік сәулелену69

7. 4 Қауіпсіздік техникасы72

7. 5 Өрт қауіпсіздігі73

7. 6 Вентиляция жүйесін есептеу74

7. 7 Жарықтандыруды есептеу76

АҢДАТПА

Бұл дипломдық жобада нейрондық желілер қаражаттық қатарлардың деңгейін жорамалдауға қолданылады.

Экономикаға қатысты проблеманың бірі - қаражаттық қатарлар. Олар күрделі жүйе болып табылады да, сондықтан математикалық модель құру негізінде олардың тәртібінің динамикасын баяндау іс-жүзінде ешқандай табыс әкелген жоқ. Бұл негізінен модельдердің тым жеңілдеуімен және де финанстық деңгей тәртібіне смежный экономикалық жүйелердің әсер ету дәрежесін толық білмеуімен түсіндіріледі. Нейрондық жүйелерді пайдалану ерекшелігі олардың салыстырмалы түрдегі аз мінездемелерге сүйеніп қандай да болмасын процессте заңдылықтарды таба ала білуде.

Жұмыс істеу кезінде нейрондық желілер бейсызықты апроксиматорымен құрылады, ал ол аяғында жеткілікті түрдегі нақты тұрақты модель ретінде құрылады және де осы модель дипломдық жобада баяндалады.

АННОТАЦИЯ

В данном дипломном проекте нейронные сети используются для прогнозирования уровня финансовых рядов.

Одной из естественных проблем, касающихся экономики являются финансовые ряды, которые представляют собой сложную систему, попытки описания динамики его поведения, путем построения математических моделей, к сожалению, как показала практика, не принесли успеха. Что в основном объясняется сильной упрощенностью самих моделей, а также недостаточными знаниями о степени влияния на поведение финансового уровня смежных экономических систем. Особенностью использования нейронных сетей является их уникальная возможность находить закономерности в поведении какого-либо процесса, опираясь на относительно небольшое число его характеристик. В процессе функционирования нейронные сети строятся нелинейным аппроксиматором, который в конечном виде представляет собой достаточно точную устойчивую модель, которая описывается в дипломной работе.

ANNOTATION

In this diploma project neirons of a network are used for forecasting a level of financial numbers(lines) . One of natural problems concerning economy are financial numbers(lines), which represent complex(difficult) system, attempts of the description of dynamics(changes) of his(its) behaviour, by construction of mathematical models, unfortunately, as the practice has shown, have not brought success. That basically is explained strong of models, and also unsufficient knowledge of a degree of influence on behaviour of a financial level of adjacent economic systems.

Feature of use neirons of networks is their unique opportunity to find laws in behaviour any of process, leaning(basing) on rather small number of his(its) characteristics. During functioning neirons of a network are under construction nonlinear approcsimators, which in a final kind represents exact enough steady model, which is described in degree work.

1 ЖАСАНДЫ НЕЙРОНДЫҚ ЖЕЛІЛЕР

Жасанды нейрондық желі ретінде ақпарат өңдеу есептеуіш құрылғысы түсініледі. Ол байланыстар немесе синапстар деп аталатын ақпарат алмасу бауларымен өзара байланысқан параллельді жұмыс істеуші қарапайым процессорлық элементтердің үлкен сандары - нейрондардан тұрады. Нейрондық желіде сыртқы әлемнен хабар алатын байланыстардың тобы және нейрондық желінің берілетін сигналдарды алынатын шығыс байланыстардың тобы болады. Нейрондық желілер классификация мен жобалаудың әр түрлі есептерін шешу үшін қолданылады. Нейрондық желі "есептер жинағы" деп аталатын оқытушы сұрыптау негізінде есепті шешуіне оқытылады. "Есептер жинағы" "кіріс - қажетті шығыс" терімдер жинағынан құрылады да, одан әрі оқытушы сұрыптауына кірмейтін мысалдарды шешу қабілетіне ие болады [1, 2] .

1. 1 Нейрондық желілердің элементтері

Нейроақпараттануда алгоритмдер мен құрылғыларды суреттеуіне арналған арнайы "схемотехника" арналып шығарылған, онда элементарлық құрылғылар - сумматорлар, синапстар, нейрондар және т. с. с. есеп шешуге арналған желілерге бірігеді.

Нейрожүйелердің ең еңбегі сіңген және маңызды элементі - адаптивті сумматор. Адаптивті сумматор x кіріс сигналының векторының α параметрінің векторына скаляр көбейтіндісін есептейді. Схемаларда оны 1. 1 суретте көрсетілгендей белгілейміз. Сумматордың адаптивті деп аталу себебі - α-ның қалпына келтірілетін параметрлерінің векторы бар болуына байланысты. Көптеген есептер үшін шығыс сигналдардың сызықты біркелкісіз функциясының бар болуы пайдалы. Оның есептеуін n+1 кірісі бар және 0-ші кірісіне тұрақты бірлік сигнал алатын адаптивті сумматор түрінде келтіруге болады (1. 2 сурет) .

1. 3 суретте бейсызықты сигнал түрлендіргіші бейнеленген. Ол x скалярлық кіріс сигналын алады да, оны ϕ( x ) -ке аударады.

Тараулану нүктесі бір сигналды бірнеше мекенжайларға жіберуі үшін қызмет етеді (1. 4 сурет) . Ол x скалярлық кіріс сигналын алады және оны өз шығыстардың бәріне тапсырады.

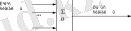
Сурет 1. 1 - Адаптивті сумматор Сурет 1. 2 - Біркелкісіз адаптивті сумматор

Сурет 1. 3 - Біркелкісіз сигнал түрлендіргіші Сурет 1. 4 - Тараулану нүктесі

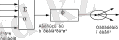
Сурет 1. 5 - Формальді нейрон

Стандартты формалдық нейрон кіріс сумматордан, бейсызықты түрлендіргіштен және тараулану нүктесінен құрастырылған (1. 5 сурет) .

Сызықты байланыс - синапс -сумматорлардан бөлек кездеспейді, бірақ кейбір ой жүгіртулер үшін мына элементті ерекше атап көрсету ыңғайлы (1. 6 сурет) . Ол x кіріс сигналын a "синапс салмағына" көбейтеді.

Сурет 1. 6 - Сызықты байланыс (синапс)

Желінің синапстарының салмақтары адаптивті параметрлердің терімін құрастырады, оларды реттей отырып нейрондық желі есепті шешуге оқиды. Әдетте синапстардың салмақтарының өзгерту диапозонына қандай да бір шек қойылады, мысалы, синапс салмағының [-1, 1] диапозонына жатуы.

1. 2 Нейрондық желілердің сәулеті

Нейрожелілік сәулеттерінің жиынынан екі негізгі сәулетін ерекше атап көрсетуге болады - қабатты және толық байланысты.

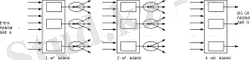
Сурет 1. 7 - Қабатты желі

Қабатты желілер: нейрондар бірнеше қабатта орналасқан (1. 7 сурет) . Бірінші қабаттың нейрондары кіріс сигналдарын алады да, оларды түрлендіріп, тараулану нүктелері арқылы екінші қабаттың нейрондарына береді. Одан әрі екінші қабаты орындалады және т. с. с. шығыс сигналдарын беретін k-шы қабатқа дейін. Егер басқа жағдай ерекше атап көрсетілмесе, i-ші қабаттың әрбір шығыс сигналы i+1-ші қабаттың барлық нейрондарының кірісіне беріледі. Әрбір қабатта нейрондардың саны кез келген болуы мүмкін және басқа қабаттардағы нейрондардың санымен ешбір алдын ала байланыспаған. Кіріс сигналдардың стандартты беру тәсілі: бірінші қабаттың әрбір нейроны барлық кіріс сигналдарын алады. Үш қабатты желілер ерекше тарату алды, оларда әрбір қабаттың өзінің аты бар: бірінші - кіріс, екінші - жасырылу, үшінші - шығыс.

Толық байланысты желілер: нейрондардың бір қабаты бар; әрбір нейрон өз шығыс сигналын қалған нейрондарға береді, өзіңе де қоса. Желінің шығыс сигналдары барлығы немесе желі жұмыс істеуінің бірнеше сатылардан кейінгі кейбір шығыс сигналдары бола алады. Барлық кіріс сигналдары нейрондардың бәріне беріледі.

Қабатты мен толық байланысты желілердің элементтері әр түрлі таңдалуы мүмкін. Дегенмен, стандартты таңдау бар - кірісінде адаптивті біркелкісіз сызықты сумматоры бар нейрон (1. 5 сурет) .

Осы жұмыста одан әрі тек қабатты нейрондық желілер ғана қарастырылатын болады, өйткені олар мәліметтерден білім өндіру есептерін шешуге арналған ең үйлесімді (сәулеті бойынша) болады.

1. 3 Есептерді нейрондық желілерімен баяндау

Оқытылатын нейрондық желілер шеше алатын есептердің екі класын атап көрсетуге болады. Бұл классификация мен болжау есептері.

Күні бұрын айту немесе болжаудың есептері негізінен шығыс мәліметтердің кіріс мәліметтеріне регресстік тәуелділікті құру есебі болып табылады. Нейрондық желілер өте бейсызықты регресстік тәуелділіктерді нәтижелі құра алады. Негізінен формализацияламаған есептер шешілетіндіктен, пайдаланушыны ең алдымен түсінікті және теориялық негізінде дәлелденген тәуелділікті құру емес, алдын ала болжаушы құралын алуы ынталандырады, негізгі ерекшелігі де осында. Осындай құрылғының болжауы бірден пайдаланылмайды - пайдаланушы нейрожелінің шығыс сигналын өз білімдерінің негізінде бағалайды да, өзінің меншікті эксперттік нәтижесін қалыптастырады. Оқытылған нейрондық желі негізінде техникалық жүйеге арналған басқару құрылғысын жасайтын жағдайлар ғана ерекше болады.

Классификация есептерін шешкенде нейрондық желі қасиеттік кеңістікте бөлуші бетін салады, ал жағдайдың бұл немесе басқа класқа жатуы туралы шешімі дербес, желіге тәуелсіз құрылғысымен - желі жауабының интерпретаторымен қабылданады. Ең қарапайым интерпретатор бинарлық классификация (екі класқа классификациялау) есебін шешкенде пайда болады. Бұл жағдайда желінің бір шығыс сигналы жеткілікті, ал интерпретатор, мысалы, егер шығыс сигналы нольден кіші болса жағдайды бірінші класқа, және егер ол нольден үлкен немесе нольге тең болса екінші класқа жатқызады.

Бірнеше класқа классификациялау интепретатордың күрделендіруін талап етеді. "Жеңуші барлығын ала кетеді" деген интерпретаторы кең қолданылады, онда желінің шығыс сигналдарының саны кластардың санына тең, ал класс нөмірі ең үлкен шығыс сигналының нөміріне сәйкес келеді.

Бір нейрон желісі бір уақытта бірнеше сандарды алдын ала болжай алады, немесе классификация және болжаудың есептерін бір уақытта шеше алады. Бірақ осындай түрлі жағдайдың қажеттілігі аса сирек кездеседі, және әр түрлі мақсаттағы есептерді бөлек нейрондық желілерімен шешу жақсырақ болады.

1. 4 Желіге кіріс сигналдарын беру және шығыс сигналдарын алу

Әдетте желінің синапстарының салмақтарына қандай да бір диапозонына жатуы талап етіледі. Нейрондардың ең жиі қолданылатын бейсызықты функциялары қандай да бір диапозонынан мән қабылдайды. Бұл желіге кіріс сигналдарын олардың нағыз диапозонында бере алмауына және керекті диапозонында шығыс сигналдарын ала алмауына әкеліп соғады.

Сондықтан желіге кіріс сигналдарын беру алдында оларды нормалау қажет, мысалы, оң болуы қажетті болса, [-1, 1] немесе [0, 1] мәндер диапозонына, немесе кіріс сигналдары осы кесінділердің шектерінен тым асып кетпеуін қадағалау қажет. Ең қарапайым нормалауды осылай орындауға болады. Кіріс мәліметтер векторының әрбір компонентасы x _i осындай мөлшермен ауыстырылады:

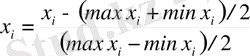Equation. 3, (1. 1)

мұндағы max x _i мен min x _i - бұл осы компонентаның бүкіл оқытушы сұрыптауы бойынша есептелген максималды және минималды мәндері. Дәл осы формула бойынша жауап векторының компоненттері қайта есептеледі.

Басқаша да нормалауға болады, мысалы, мәліметтер шашуы дербес болатындай сұрыптауды түгендеу. Бірақ осында бір қиындық болады. Оқытушы сұрыптаудың кез келген өзгертуі сәйкес тиісті мәліметтердің нормалау ережесін де алмастыруы керек. Сондықтан әдетте осылай істейді: min және max -мөлшерлері ретінде қазіргі кезеңінде бар есептер жинағынан мәліметтерді алады, және де бұдан былай нормалауды алмастырмайды, ал егер бұдан былай тым көп айырмашылығы бар мәліметтер түсетіні шамаланса, min және max -мөлшерлері пайдаланушы бағалауларымен қойылады. Басқаша айтқанда, бұл мөлшерлер желі құрылған кезеңінде енгізілуі керек және де бұдан былай оқытушы сұрыптаудан тәуелді болмау қажет. Желінің шығыс сигналдары айналған формулаларымен нағыз мәндердің диапозонына тиісті нормалануы қажет .

Желілер-классификаторлар үшін шығыс сигналдарын нормалаудың қажеті жоқ, өйткені пайдаланушы желінің шығыс сигналдарын емес, жауап интерпретаторымен жағдайды бір немесе басқа бір класына жатқызу нәтижесін алады. Осы жағдайда есептер жинағының әрбір шығыс векторы жауап интерпретаторымен дұрыс өңделу үшін қайта құрылады. Мысалы, "жеңуші барлығын ала кетеді" деген интерпретаторымен үш класқа классификациялау кезінде класстың нөмірі үш сандарынан тұратын векторымен кодталады, онда класс нөміріне лайықты вектордың компонентасы 1 деген мәніне ие болады, ал қалған екеуі -1 деген мән алады.

Басқа бір проблема - мәліметтердің кестесінде бос орындар болатын жағдай болады. Мәліметтердің осындай жоқ болатын компоненталардың орнына ноль беруге болады, оқытушы сұрыптауынан жинақтамаған векторларды шығаруға болады, желіні оқыту алдында бос орындарын қандай да бір шынайы мәндерімен толтыру есебін шешуге болады. Соңғысы дербес, жиі кездесетін және жеткілікті түрдегі күрделі проблема болып табылады.

1. 5 Нейрондық желілерді оқыту

"Есептер жинағында" нейрондық желіні оқыту дегеніміз желінің шығыс сигналдары мен анықталуы қажетті сигналдарының арасындағы қандай да бір байланыспау функционалын минимизациялауды айтамыз. Байланыспау функционалын (бұдан былай бағалауды) минимизациялау деп желінің нейрондарының a _i оқытылатын параметрлерінің желі X сигналдарының кіріс векторына талап етілетін Y жауабына барынша жақынырақ болатын Y' жауап беретіндей жанастырылуы. Басқаша айтқанда, мысалдар саны N (яғни, N жұбы үшін { X _i , Y _i }, i =1, . ., N) болатын есептер жинағы бағалаудың жиынтық функциясының минимумына:

жетуі керек.

Норма функциясы ретінде Y-Y' векторының элементтерінің квадраттардың сәйкес компонентті қосындысы (МНК бағалауы) немесе көбірек мамандандырылған функциясы қарастырылады. Көбірек мамандандырылған бағалауларды қолдану желіні оқыту процесін тездетеді. Дәл осылай, есептің шешімінің дәлдігіне талаптар қоя алатын бағалаулар қолдануға болады. Бұл пайдаланушыны қанағаттандыратын дәлдігіне жеткенде оқу процесін тоқтатуға рұқсат етеді. Мысалы, люфт түрі келесідей болатын МНК бағалауын пайдалануға болады:

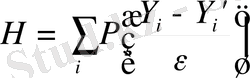, (1. 2)

мұндағы

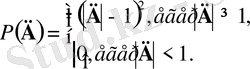
Люфті ε болатын бағалаулары байланыспаудың берілген мөлшеріне жеткенде оптимизацияны тоқтата алады.

Бағалау функциясының минимизациясы оптимизацияның градиентті әдістерінің пайдалануымен орындалады. Желінің құрылымын қандай да бір ережелерімен түрлендіріп, желінің шығысына шығыс сигналдарының бағалау функцияларының жеке туындыларын беріп және екі жақты функционалдығын қолдана отырып, біз желінің әрбір ішкі құрылған параметрі мен әрбір кіріс сигналы үшін бұл параметрдің немесе сигналдың бағалау функцияларының жеке туындыларын ала аламыз. Желінің параметрлерінің векторына сәйкес лайықты жеке туындылардың векторы бағалау функциясының градиенті болады, сондықтан бағалау функциясының градиентті ықшамдауы мүмкін, оның барысында нейрондық желі оған берілетін кіріс сигналдарына талап етілетін жауаптар беруіне "оқытылады". Желіні жиынтық градиенті (толық есептер жинағы бойынша градиенті) бойынша оқыту жақсырақ болады, бұл оқыту процесін тездетеді, және қарапайым градиентті түсірудің үстіне қосылатын мамандандырылған оптимизация алгоритмдерін қолдану керек. Жиынтық градиентін есептеу үшін есептер жинағының әрбір үлгісіне есептелетін градиенттердің векторларын қосу керек, (барлығы N вектор) .

1. 5. 1 Желінің жолдық параметрлері бойынша бағалау функциясының градиентін есептеу

Енді қазір, желінің ішкі құрылған параметрлері бойынша бағалау функциясының градиенті қалай есептелетінін қарастырайық. Градиентті есептеу берілген нейрондық желісіне екі жақтылықты нейрондық желісінің жұмыс істеуі кезінде іске асырылады . Екі жақтылықты желісінде сигналдар кері бағытта беріледі - желісінің шығысынан оның кірісіне, ал екі жақтылықты желі құрылатын элементтері, берілген элеметтеріне екі жақтылықты болады. Ең алдымен желінің жеткілікті түрдегі абстрактілі элементті қарап шығамыз. Оған x _i айнымалыларының n мәндері беріледі, олардың негізде f(x ₁ , …x _n ) функциясының мәні есептеледі және де бұл мән m шығыс байланыстарына жіберіледі. Екі жақтылықты желісінде бұл элемент шығысында μ _i екі жақтылықты сигналдарының m терімін алады да, олардың қосындысын μ есептейді де әрбір n кірістеріне μ мен сигналдың сәйкес кірісіне берілетін мәні бойынша жеке туынды функциясының f(x ₁ , …x _n ) туындысының көбейтіндісін береді. Бұл процесс 1. 8 суретте көрсетілген. Онда екі жақтылықты желі құрылғанда барлық тараулану нүктелері оларға екі жақтылықты элементтеріне - қарапайым сумматорларға көшетіні көрінеді.

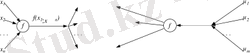
Сурет 1. 8 - Нейрожелісінің абстрактілі элементінің тура және екі жақтылықты функционалуы

Енді формалді нейронға екі жақтылықты нейронды құру процесін қарастырамыз. Ол үшін формалді нейронды (1. 5 сурет) толығырақ қарастырайық (1. 9 сурет), онда нейронның кіріс адаптивті сумматорын жұптық (синапс салмағы мен синапсқа келуші сигналдың) көбейтіндісін есептейтін элементтердің терімі мен қарапайым сумматор түрінде қарайық. Формалді нейронды құрастыратын барлық элементтерін жоғарыда баяндалған екі жақтылықты элемент құру ережеге сәйкес қайта құрамыз. Формалді нейронға екі жақтылықты нейрон және оның жұмыс істеу ережелері 1. 10-ші суретте көрсетілген. Осында екі жақтылықты желіні құрғанда барлық қарапайым сумматорлар оларға екі жақтылықты элементтеріне - тараулану нүктелеріне өтетіні көрінеді. Осы фактіні көбірек көркемдеу үшін 1. 9-ші суретте адаптивті сумматорды қарапайым сумматоры мен синапстардың терімі түрінде ұсынуы қолданылған болатын. Екі жақтылықты желісі формалді нейрондарға екі жақтылықты нейрондарынан құрылады. Әрине, екі жақтылықты желілер нейрондардың контрукциясы күрделірек болатын желілер үшін де құрылуы мүмкін.

Сурет 1. 9 - Формальді нейронның функционалуы

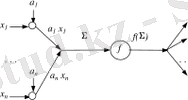
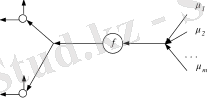
Сурет 1. 10 - Формальді нейронның екі жақтылықты функционалуы

Сонымен, берілген желісіне екі жақтылықты желі құрылды. Енді қазір соңғы қабаттың нейрондарының шығысына берілетін екі жақтылықты айнымалыларын μ анықтаймыз. Екі жақтылықты желі көмегімен берілген желісінің ішкі құрылған параметрлері бойынша бағалау функциясының градиентін есептеу есебін шешу үшін, екі жақтылықты айнымалылары ретінде желінің шығыс сигналдары бойынша бағалау функциясының жеке туындыларын H алу қажетті. Онда желінің барлық элементтері мен кіріс сигналдары үшін бұл параметрлердің мен сигналдардың мәндері бойынша бағалау функцияларының жеке туындылары есептеп шығарылған болады.

Градиент есептеуіне екі жақтылықты желіні қолдану градиенттің бүкіл векторын есептеу уақыты берілген желісінің әдеттегі жұмыс істеуі кезіндегі шығыс сигналдарын есептеу уақытысынан не бары 2-3 есе үлкен болады. Бұның себебі, барлық орындалатын әрекеттердің ұйымшыл болуы, есептеулердің қайталаусыз іске асырылған, және де градиент барынша көп параллельді тәртіпте есептеледі.

Градиенттің есептеуіне екі жақтылықты жұмыс істеуін қолдану үшін нейрондық желілер мен бағалау функциясына қойылатын жалғыз талабы ол бағалау функциялары мен желісінің барлық элементтерінің олардың кіріс сигналдары бойынша үзіліссіз бірінші туындыларының бар болуы.

1. 5. 2 Нейрондық желі оқытуына әсер ететін факторлар

Нейрондық желісінің есепті дұрыс шешуіне оқытуының табыстылығы тәуелді болатын факторларды қарастырайық. Ең алдымен, желі оқытушы сұрыптаудың барлық үлгілерін дұрыс шешуге үйрену үшін жеткілікті түрде иілгіш болу керек. Сондықтан нейрондық желісінде нейрондардың және байланыстардың жеткілікті көлемі болу керек.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.