Рид-Соломон кодтары негізіндегі телемеханикалық ақпараттарды жіберу әдістері мен құралдарын жобалау


Рид-Соломон коды
МАЗМҰНЫ
1 ТЕЛЕМЕХАНИКАЛЫҚ АҚПАРАТТЫ ЖІБЕРУ2
1. 1. Ақпаратты жіберу және қабылдау процесінде ақпараттың маңызы2
2. АҚПАРАТТАРДЫ ЖІБЕРУ ЖӘНЕ ҚАБЫЛДАУ ҚОЛДАНАТЫН КОДТАР3
2. 1. Ақпараттарды жіберудегі және қабылдаудағы негізгі анықтамалар. 3
2. 2 БҰРМАЛАНБАҒАН КОДТАР6
2. 3 БҰРМАЛАНҒАН КОДТАР6
2. 4 АЙНЫМАЛЫ КОДТАР8
3. ЕКІЛІК ЕМЕС АЙНЫМАЛЫ РИД-СОЛОМОН КОДЫНДА У АРҚЫЛЫ АҚПАРАТТЫ ЖІБЕРУ11
3. 1. Рид- Соломон кодтарының сипаттамасы19
3. 2 Көпмүшелікті құрайтын символдарды таңдау20
3. 3 Кодалау22
3. 4 Кері кодалау23
4. РИД-СОЛОМОН КОДАНЫҢ ФУНКЦИЯНАЛДЫ СҰЛБАСЫН ЖҮЗЕГЕ АСЫРУ24
4. 1. Сызықты қайта қосу сұлбалары24
4. 2. Бөлу сұлбасы26
5. РИД-СОЛОМОН КОДЫНЫҢ ҚАҒИДАЛЫ СҰЛБАЛАРЫН ЖАСАУ. 31
5. 1 Кодтаушы құрылғының қағидалы сұлбасы. 31
5. 2. Рид - Соломон кодының керікодтау құрылғысының қағидалы сұлбасы. 36
6. ДАЙЫНДАУ ТЕХНОЛОГИЯСЫ МЕН КОНСТРУКЦИЯСЫ. 38
7. БАҒДАРЛАМАЛЫ ҚАМТАМАСЫЗ ЕТУ39
7. 1 Модуль екі бойынша логикалық элементтің қосындылауышы39
7. 2 Рид-Соломон кодтарын көбейту процедурасы. 42
7. 3. Көпмүшеліктерді көпмүшеліктерге бөлу процедурасы44
7. 4. Кодтаудың ішкі бағдарламасы46
7. 5. Керікодтаудың ішкі бағдарламасы48
ҚОРЫТЫНДЫ50
АННОТАЦИЯ
Дипломдық жұмыста айналмалы кодтар қарастырылған, оның ішінде екілік емес айнымалы Рид-Соломон кодтарын қолдану негізінде телемеханикалық ақпараттарды беру әдістері мен құралдарын жобалау проблемаларын көрсеткен.
Арналар желісі мен ақпараттарды сақтаудың кеңінен таратылуынан, 2 а көлемді алфавит символдарының пайдалануы компьютерлі ЭВМ көмегімен ақпараттарды өңдеу құралдарының дамуымен түсіндіріледі.
Ақпаратты жіберу және қабылдау процесін басқару кезінде, өндірістік процестерде хабар пайда болады, яғни құрылғының бір үзбесінен басқасына беру қажет. Бұл хабар, әртүрлі хабарлармен туындалады, мысалы берілетін шикізаттың құрамының өзгерісі, қоршаған ортаның температурасының жоғарлауымен байланысты, хабарды жоғары эффектілікпен беру үшін, сигналды жақсы жағынан, байланыс желісінің өтімділігінің максималдығын қамтамасыз ету керек, яғни ақпараттың санын бөгеуілсіз беру қажеттігі туады, сондықтан да осы дипломдық жобадағы қарастырылған Рид-Соломон кодтары келешекте кеңінен пайдаланылады.
Жасалған дипломдық жобаның тапсырмасы бойынша Рид-Соломон кодтарын қолдану негізінде телемеханикалық ақпараттарды беру әдістері мен құралдарын жобалау. Жұмыста әртүрлі мәселелерді қарастырады, басқаша айтқанда, кодтармен танысу, көпмүшеліктердің жасаушыларын таңдау, түзгіштердің және кері түзгіштердің сұлбаларын жобалау, түзгіштердің және керітүзгіштердің функционалдық және қағидалық сұлбаларын, конструкциясын жобалау, еңбекті қорғау және экономикалық сұрақтары қарастырылады.
1 ТЕЛЕМЕХАНИКАЛЫҚ АҚПАРАТТЫ ЖІБЕРУ
1. 1. Ақпаратты жіберу және қабылдау процесінде ақпараттың маңызы
Ақпаратты жіберу және қабылдауда процестерді басқару, өндірістік процестерде хабар пайда болады, яғни құрылғының бір үзбесінен басқасына беру қажет. Бұл хабар, әртүрлі хабарлармен туындалады, мысалы берілетін шикізаттың құрамының өзгерісі, қоршаған ортаның температурасының жоғарлауымен байланысты, хабарды жоғары эффектілікпен беру үшін, сигналды жақсы жағынан, байланыс арнасының өтімділігінің максималдығын қамтамасыз ету керек, яғни ақпараттың санын бөгеуілсіз беру қажет.
Арна желісі арқылы ақпаратты беру үшін, мынадай физикалық процесті қолдану қажет, яғни біріншіден ол эфир және байланыс арнасы арқылы таратылу керек және екіншіден, өздерінің параметрлерін өзгерту қажет. Телемеханикада көбінесе ақпаратты алып жүрушілер ретінде электрлі толқындар, импульстер және айнымалы ток түрінде қолданылады.
Өзгерулі кернеу айнымалы ток, амплитудамен, жиілік пен фазамен сипатталады. Бұл айнымалы ток параметрлерінің өзгерулері модуляция көмегімен жүзеге асады. Телемеханикада импульс мағынасы электрлік схемаға әсер ететін қысқа уақыттық электрлік ток және кернеуді түсінуге болады. Яғни ақпаратты алып жүрушілер деп аталады. Алып жүрушілер өзінің пішінін өзгерту күйімен немесе әртүрлі түрдегі хабардың әсерінен параметрлерін өзгертуі қажет. Өздігінен алып жүрушілер сигналдар болып табылмайды. Бірақ, егер алып жүрушілерге хабар әсер етпесе, онда ол сигналға айналады.
Сигнал-бұл хабардың әсер етуіндегі алып жүрушілер немесе ақпараттың әсер етуіндегі алып жүрушілер. Яғни хабар көп болса, сигналдар бір-бірінен өзгеше болуы керек және берілетін хабарға сәйкес келуі керек. Сигналдардың жіберілу мен анықталуы анықталған заң бойынша шығады.
2. АҚПАРАТТАРДЫ ЖІБЕРУ ЖӘНЕ ҚАБЫЛДАУ ҚОЛДАНАТЫН КОДТАР
2. 1. Ақпараттарды жіберудегі және қабылдаудағы негізгі анықтамалар.
Код - анықталған ақпаратты алып жүретін және анықталған алгоритм бойынша қарастырылған бүтін рационал сандардың шекті көпмүшелігі.
Мысалы, 100110; 2367; АВ34С.
Кодтың алфавиті - символдар жиыны немесе кодты құрайтын сандар.
Кодтау - код комбинациясы түріндегі хабарды үздікті сигналға айналдыру.
Кері кодтау - үздікті сигналды хабарға түрлендіру.
Түзгіш - құрылғы, ақпаратты кодқа түрлендіреді.
Керітүзгіш - кодты ақпаратқа түрлендіретін құрылғы.
Кодтардың келесі сипаттамасы бар:
1. m - түзбенің негізі, ол алфавиттегі символдарына тең;
2. n - код ұзындығы, яғни код сөзіндегі белгілер саны.
Кодтардағы n- әрқашанда біркелкі деп атайды, кері жағдайда біркелкі емес деп атайды.
3. Код қуаты - берілген кодтағы мүмкін код сөзінің саны.
4. d-код ара-қашықтығы, әртүрлі екі жақын тұрған код сөзінің санымен анықталады, әртүрлі код сөздерінің бір позициясындағы символдардың санымен өрнектеледі.
Код ара-қашықтығы, кодтаудың коррекциялаушы күйін анықтайды. Мысалы:
00-1;
01-2;
10-3;
11-4.
Бұл кодтың ара-қашықтығы бірге тең “00” себебі “01”-ден бір позицияға өзгеше болып тұр. Байланыс арқылы біз “1” жіберуіміз қажет деп қарастырайық, яғни байланыс арнасына “00” сигналы келіп түседі, егер кіші разрядтағы байланыста бөгеу болатын болса, онда қабылдағыштың соңында “01” сигналы қабылданады, ол екіге сәйкес келеді [1] .
Көрініп тұрғандай, бөгеуіл ақпараттың бөгеуіне әкеліп соғады, яғни ақпараттың дұрыс қабылданбауына бір ғана қате жеткілікті.
Басқа мысалды қарастырайық. Келесі код берілсін:
00-1;
11-2.
Көрініп тұрғандай, “00” бір сәйкес, ал екіге “11” сәйкес, яғни код ара-қашықтығы екіге тең. Егер разрядтың біреуінде бөгеу бар болатын болса, “01” немесе “10” комбинациясы жалған, бірақ берілген комбинацияны анықтау өте қиын, себебі “01” немесе “10” “00”-ден “11” тең алшақты. Бұл кодтар тек қана бірлік қателерді таба алады. Бұл кодтар өте нәзік және кең қолданылмайды.
d=3 кодын құрайық.
Мысалы: 000-1;
111-2.
“001” комбинациясы қабылданды дерлік, көрініп тұрғандай жіберу кезінде қате кетті. Берілген комбинация “000” тең ықтималды, яғни біз бірлік қатені таптық және оны түзетуімізге болады. Басқа жағынан екілік қате кетті деуге нақтылы айтуға болмайды, яғни код тек қана бірлік қатені жөндейді немесе екілік қатені табады. Бірақ, мұндай жол қолайсыз, себебі код ара-қашықтығын үлкейту, оның өсуіне және қуаты мен ақпарат тығыздығының, код ұзындығының өсуіне әкеліп соғады. Бұның шешімі, арнайы кодтау, яғни кодтар математикалық заңдылық бойынша қарастырылады.
К. Шеннон теоремасына сейкес әрбір арна, жіберудің жылдамдығы қажеттіліктен үлкен болса, онда кодты арнадағы болатын ықтимал қатені минималға жеткізуге болады.
Мұндай кодтарды табу өте күрделі.
Жұптылыққа түзетілген, қайталанатын Хэмминг түзбелері құрылды. Осы қатені кодтар ашылғаннан кейін бақылайтын кодтар қарастырлады. Боуз және Чоудхури кодтары шықты, еселі қатені түзететін және екілік емес Рид-Соломон кодтары ашылды.
Басқа зерттеулершілер ықтималдық теоремасынан бас тартып, өте дәл кодтарды ашты, яғни олар үздіксіз және блоктар құрылды.
Бақыланған шамалардың үздікті мәнін беру үшін әртүрлі кодтар қолданылады. Бірақ көпшілік жағдайда сандық кодтар қолданылады. Сандық кодтар, ол импульстар тогы, оның әрбіреуі кодталанатын n - разряд саны разрядына сәйкес. Әрбір m- импульстер параметрлерінің мүмкін мәндер саны санауыштың негізіне тең. Импульстерге берілетін параметрлер мәні 0-ден m-1, түзбелер ансамбілін аламыз, 0-ден N m сандарына эквивалентті, мұндағы N m n - разряд саны бар m санағыштың негізі.
N m = m n - 1 (1)
Көп тараған екілік сан жүйесіндегі сигналдар түзбесі
N m = 2 n - 1 (2)
Беруді ыңғайлататын біркелкі кодтар қолданылады [2] .
2. 2 БҰРМАЛАНБАҒАН КОДТАР
Бұрмаланбаған кодтардың ерекшелігі, олардың құрамында болатын түзбе комбинациялары, бір-бірінен бір разрядқа ғана өзгешелігінде болып табылады, яғни d=1.
Мұндай түзбелер ақпаратты алып жүрушілердің арасындағы ең кең тараған түрі болып табылады.
Мысалы, төртразрядты екілік түзбе:
- (0) ; 1000 - (8) ;
0001 - (1) ; 1001 - (9) ;
0010 - (2) ; 1010 - (10) ;
0011 - (3) ; 1011 - (11) ;
0100 - (4) ; 1100 - (12) ;
0101 - (5) ; 1101 - (13) ;
0110 - (6) ; 1110 - (14) ;
0111 - (7) ; - (15) .
Көрініп тұрғандай, екі код немесе код сөздерінің арақашықтығы бірге тең, яғни d=1, сәйкесінше екілік код үшін Хэмминг ара-қашықтығы бірге тең. Осыдан шығатыны, бөгелуге тұра алмайтын екілік кодтарды телемеханикалық ақпараттарды байланыс арнасы арқылы жіберу абсолютті түрде мүмкін емес.
Жоғарыда айтылған кемшіліктер бойынша телемеханикада бұрмаланбаған кодтар қолданылмайды. Бұрмаланбаған кодтар кәдімгі кодтар деп аталады. Бүл кодтарға жататындар: екілік кодтар, Грей коды, бірлік-ондық код, екілік-ондық код, санды импульсті код Морзе коды. Бодо коды, халықаралық телеграф коды.
2. 3 БҰРМАЛАНҒАН КОДТАР
Қазіргі кезде қателерді табатын кодтардың бірнеше түрі белгілі. Көбінесе олар блок кодтар болып табылады, яғни n- символдан тұратын блоктар берілген, соның ішінде r-бақыланатын және k-ақпараттық символдар.
Блоктық кодтарды қолдану өте ыңғайлы, себебі егер қате кететіндей болса және ол табылып, бірақ түзетілмеген болса, онда бұл берілген блокты “жарамсыз” деп, қатені блоктың шегінен тыс шығарылмайды.
Жұптылыққа тексеруші түзбе.
Мұндай к- ақпарат символдарынан тұратын ақпаратты толықтыру жолымен жүзеге асады, бірақ m - (0 немесе 1) бақыланатын символдағы жалпы бірлер болу керек.
Қабылданатын жағында модул екі бойынша келіп түсетін символдарды қосындылауышы жүргізіледі. Егер символдар соммасы нөлге тең болса, онда қате жоқ немесе жұп сан қате кетті.
Комбинациядағы тұрақты нөлдер мен бірлер бар кодтар. Мұндай кодтарды тұрақты салмағы бар түзбелер деп атайды. Мұндай кодтардағы әрбір блоктың ішінде қатаң түрде орналасқан тұрақты нөлдер және бірлер сандары бар.
Мысалы, екілік бірдер бар бірразрядты код. Бұл кодтар бөгеуге тұра алады және көптеген бөгеулер санын таба алады.
00011 - (1) ;
00101 - (2) ;
01001 - (3) ;
10010 - (4) ;
11000 - (5) ;
Кодтағы кодтар комбинацияларын дұрыс қабылдануы, бірлердің мөлшерін санау арқылы анықталады және егер, мысалы кодтағы екі бір саны қабылданса, онда жіберуде қате кеткен. Код ара-қашықтығы екіге тең, яғни ол барлық бірлік қателерді таба алады.
Сонымен қатар, бұл код көпшілік бөлімдерін таба алады, егер бір нөлге ауысса, ал нөльдің біреуі бірге ауысатын болса, онда ол қателердің бөлімдерін таба алмайды. Аралас бөгеу жағдайда да табылмайды.
Таратылатын код та позициялық деп аталады. Фактілі түрде ол тұрақты салмақты деп саналады, ондағы бірлер саны бірге тең, ал басқа символдар нөлге тең. Бұл кодтар қатеден жақсы қорғалған және қодануға ыңғайлы, бірақ ақпарат тығыздығы өте төмен.
Жіберу кезінде ақпарат блогы қайталанады, 110 110110. Бұл кодтың жақсы коррекциялаушы мүмкіндігі бар, бірақ көп шығындалады, сондықтан оны өте жоғары нақтылы ақпарат үшін қолданады, ал разрядтың мәні ескерілмейді [1] .
Бұрмаланған кодтарға инверсиялы кодтар жатады. Бұл кодтардың бұрмаланған қабілетін жоғарылату үшін n- разрядты комбинациядағы анықталған ереже бойынша, тағы да n- разрядтар қосылады. Нәтижесінде сызықты еселенген символдар саны жіберіледі.
Түзбенің орналасу ережесі келесі: егер берілген комбинацияларда бірдің саны жұп болса, онда комбинация берілгенді қайталайды, егер тақ болса, онда қосылатын разрядтағы барлық нөлдер нөлге айналады, ал бірлер нөлге айналады.
2. 4 АЙНЫМАЛЫ КОДТАР
Ұсынылып отырған Рид-Соломон коды айнымалы кодтар болып табылады. Нақты, Рид-Соломон кодының ақпараттық және бағдарламалық жүзеге асуы, екілік айнымалы кодтармен көптеген байланыстары бар. Сондықтан да оларды терең қарастырамыз.
Айнымалы кодтар теориясы, топтар теориясы мен Галуа өрісіндегі көпмүшелік алгебрасына (базаланады, сүйенеді) негізделеді.
Айнымалы кодтар блокты жүйелі кодтар қатарына жатады, ондағы әрбір комбинация өздігінен түзбеленеді, яғни к - ақпарат және m - бақыланатын символдар анықталған орындарда орналасқан. Сонымен қатар, әрбір қатені жөндей алу мүмкіндігі жоғары және аппаратураны жүзеге асыру сызбасының қарапайымдылығы, осы кодтарды қолдануға мүмкіндік береді.
Белгілі жағдайда, көпмүшелік берілген өрістегі коэфициенттері бар төменгі дәрежелі көпмүшеліктің жасаушысы түрінде көрсетуге болыды және оны келтірілген деп атайды. Керісінше жағдайда, келтірілмеген деп атайды.
Бұл келтірілмеген көпмүшелікті Р(x) екілік немесе ондық сандар түрінде жазуға болады немесе алгебралық көпмүшелік түрінде, төменде айналмалы кодтарды құру үшін қолданылатын келтірілмеген көпмүшеліктер үшін кесте келтірілген. Екілік сан өрісіндегі көпмұшелікті келтірілмеген деп атайды, егер ол қалдықсыз бөлінетін болса.
Айналмалы кодтау негізінде Р(x) келтірілмеген көпмүшелікті қолдану жатқызылады, яғни айналмалы кодтарда қолданылатын осы көпмүшеліктің дәрежесі бақыланатын символдар санынан кіші болмау керек және нөлдік емес мүшелер саны код ара-қашықтығынан көп қажет. Сонымен қатар, яғни қалдықсыз бөлінетін. Кейбір көпмүшеліктер кесте 1-де көрсетілген.
Айнымалы кодтың кодтау комбинациясының берілген кодтау комбинациясының көпмүшелігін бөлу арқылы орындалады, немесе көбейту арқыыл. Кері кодтау сол сияқты көбейту немесе бөлу арқылы жүзеге асады. Егер қалдық жоқ болса, онда қабылдау және кері кодтау дұрыс орындалады, егер қалдық нөлге тең болса, онда оның мәнінде қате бар деп саналады, олардың санында және дислокациясында деп аталады.
Телемеханикадағы айнымалы кодтар өте ыңғайлығ яғни аппараттық жүзеге асыру кезінде кодтар тізбекті болуы керек. Сол себептен байланыс саны азаяды [2] .
Кесте 1 - Ондық дәрежеге дейінгі қарапайым көпмүшеліктер
 Equation. 3
Equation. 3
Кесте 1. жалғасы - Ондық дәрежеге дейінгі қарапайым көпмүшеліктер
3. ЕКІЛІК ЕМЕС АЙНЫМАЛЫ РИД-СОЛОМОН КОДЫНДА У АРҚЫЛЫ АҚПАРАТТЫ ЖІБЕРУ
Қатені түзейтін екілік кодтардың жетіспеушілігі - байланыс сызығының аз толықтырылуы. Байланыс сызығы арқылы екі сигнал ғана өтеді, 0 және 1 сигналы, ал осы мүмкін уақытта сызықтың мүмкіндігі кіші үзділікті және көп үздікті деңгейдің саны қабылданады.
Байланыс арасындағы бөгеуілдерден болатын қателер және сақтау арнасындағы алып жүрушілердің яизикалық жараққаттануы салдарынан көп ақпаратты енгізу қажет етіледі және олар сақталуы керек. 2 а негізі бар кодтары екілікті ақпаратты кодтарды өңдеу, құрылғының кодтау және керікодтауының жүзеге асуына қарапайым мүмкіндік беру.
Оларға 2 а негізі бар сызықты блокты кодтар жатады.
Кодтау әдісі және жалпы сипаттамасы.
Егер әрбір 2 а екілік емес векторлардың а- ұзындығы бар екілік емемс алфавиттен символдардың біреуін алып салыстырсақ, онда к• а ұзындықты екілік тізбектің орнына к- ұзындықты эквивалентті екілік тізбекті қарастыруға болады. Мұндай ақпаратты өңдеу орнықтылықты бөгеу к=2 а негізі бар әртүрлі түзбелер көмегімен мүмкін.
(n, k) сызықты блоктың кодтар жағдайында, берілген ақпарат векторын
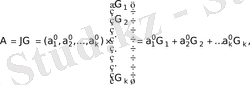 (3)
(3)
мұндағы
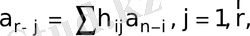 Equation. 3 (4)
Equation. 3 (4)
(3) және (4) қатынастарының өрнегі G үшін каноникалық түрде былай жазуға болады:
 (5)
(5)
мұндағы
\[\mathsf{H}=(\mathsf{R}\,,\mathsf{l}_{\mathsf{r}}),\](6)
А код векторлары Н матрицасының нөлдік кеңістігін құрайды.
\[\mathbb{A}\mathbb{H}^{\textsf{T}}=0,\]Equation. 3 (7)
Екілік емес алфавитті қосу.
Екілік емес алфавитті қосуоперациясы, сәйкес векторларды разряд бойынша (модул екі бойынша) қосу арқылы орындалады.
Мысалы:
(1011) +(0110) =(1101)
Барлық к- екілік емес ақпараттық символдары мультипликативті топты құрайды, ол өзінде 0 элементін қосады, оған сәйкесінше (00 . . . 0) векторы сәйкес, бірлік элементке (00 . . . 010) векторы сәйкес. Сонымен қатар барлық β - бүтін дәрежеден к-2 дейін сәйкес.
Сонымен қатар, барлық мультипликативті топқа айналымдық талап қойылады.
Екілік емес алфавитті көбейту.
Топтың элементтерін көбейту, эквивалентті векторлардың сақтау үшін,
 үшін 2 кестеде берілген. Яғни көбейту ережесі, кодттың разрядтылығы толып кетпеуі үшін қажет, яғни
үшін 2 кестеде берілген. Яғни көбейту ережесі, кодттың разрядтылығы толып кетпеуі үшін қажет, яғни
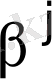 - ге бөлу
- ге бөлу
Мультипликативті топты құру үшін мысалын қарастырайық.
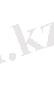
Кесте-2-
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz