ҚАЛА СЫРТЫ ЖОЛДАРЫНЫҢ ТЕМПЕРАТУРАЛЫҚ ЖАҒДАЙЫН ШЕКТІ ЭЛЕМЕНТТЕР ӘДІСІМЕН MATLAB ЖҮЙЕСІНДЕ ЗЕРТТЕУДІҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 62 бет
Таңдаулыға:

Ф-ОБ-001/003

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ

ҒЫЛЫМ МИНИСТРЛІГІ

Қ. А. Ясауи атындағы Халықаралық қазақ-түрік университеті

«Бағдарламалармен қамтамасыздандыру» кафедрасы

Д И П Л О М Д Ы Қ Ж Ұ М Ы С

Тақырыбы: MATLAB жүйесінде қала сырты автомобиль

жолдарындағы жылу таралу процестерін модельдеу

Орындаған: АБҚ-315 тобының студенті

Жұмабекова Индира

Ғылыми жетекшісі: тех. ғ. к., доцент

Айтбаев Қобланбек

Түркістан 2008

М а з м ұ н ыКіріспе . .:

М а з м ұ н ы

Кіріспе . .

3: 3

М а з м ұ н ыКіріспе . .:

І-тарау.

ҚАЛА СЫРТЫ ЖОЛДАРЫНЫҢ ТЕМПЕРАТУРАЛЫҚ ЖАҒДАЙЫН ШЕКТІ ЭЛЕМЕНТТЕР ӘДІСІМЕН MATLAB ЖҮЙЕСІНДЕ ЗЕРТТЕУДІҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ

3: 8

: 1. 1.

М а з м ұ н ыКіріспе . .: MATLAB жүйесіне кіріспе . . . ………

3: 8

: 1. 2.

М а з м ұ н ыКіріспе . .: Жол төсемелерiнiң температуралық режимiн шекті элементтер әдісімен зерттеудің теориялық негіздері . . . …. .

3: 19

М а з м ұ н ыКіріспе . .:

ІІ-тарау.

ҚАЛА СЫРТЫ ЖОЛДАРЫНЫҢ ТЕМПЕРАТУРАЛЫҚ

РЕЖИМIН ТЕОРИЯЛЫҚ ЖОЛМЕН ЗЕРТТЕУ . . .

3: 29

: 2. 1.

М а з м ұ н ыКіріспе . .:

Автомобиль жолдарының көпқабатты құрылымының

температуралық есебінің қойылуы . . .

3: 29

: 2. 2.

М а з м ұ н ыКіріспе . .: . Жол құрылымының температуралық күйінің жыл мезгiлдерiне байланысты өзгеру заңдылықтарын зерттеу . . .

3: 33

М а з м ұ н ыКіріспе . .:

НЕГIЗГI ҚОРЫТЫНДЫЛАР . . .

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТIЗIМI …… . . .

ҚОСЫМШАЛАР:

А. Есептеу программасының листингі . . .

Б. Есептеу нәтижесінің сандық кестесі . . .

КIРIСПЕ

Қазiргi кезде жоғары техникалық категориялы автомобиль жолдарында асфальт-бетон жамылғылы жол төсемесi кеңiнен таралған. Мысалы, Казақстанда пайдаланылып жүрген қатты жамылғылы автомобиль жолдарының 90-95% - да асфальт-бетон қолданылады.

Асфальт-бетон жамылғылы жол төсемесерi негiзiнен төрт, немесе одан да көп қабаттардан тұратын көп қабатты конструкция болып келедi. Әдетте, жоғарғы қабаттар асфальт-бетоннан жасалынады, ал қалған қабаттар берiктiгi төмендеу шашылғыш материалдардан тұрады. Асфальт-бетон жамылғының кернеулі-деформациялы жағдайына, демек оның берiктiгi мен жұмыс iстеу мерзiмiне көлiктердiң салмағымен қатар табиғи факторлар, ауа райының, әсiресе қоршаған ортаның температурасының өзгеру режимдерi қатты әсер етедi.

Жазғы кезде жол конструкцияларының асфальт-бетон қабаттары жоғары температуралардың әсерiне ұшырайды. Жоғары температураның әсерi көлiктердiң салмағымен қосылған кезде жол жамылғысында ығысу, ағу, төсемедегi толқындар сияқты қалдық деформациялар пайда болады.

Керiсiнше, температураның төмендеуi битумның тұтқырлығын жоғарылатып, асфальт-бетонның қатайыуына, оның деформациялық мүмкiндiктерiнiң төмендеуiне әкелiп соғады. Осының әсерiнен көлiк құралдарынан түсетiн салмақ көбейген жағдайда жол жамылғыларында жарықшақтар пайда болуы мүмкiн. Жарықшақтар әсiресе температура күрт төмендеген жағдайда жиi пайда болады. Демек, жарықшақтардың пайда болу процесiне қоршаған ортаның температурасының өзгеру жылдамдығы да әсер етедi. Оның үстiне суға қаныққан жол төсемесiнiң негiзi терiс температура әсерiнен, температураның нөлден жиi өтуiнiң әсерiнен аяздық күйреуге ұшырайды да, өзiнiң берiктiгiн жоғалтады.

Сонымен, автомобиль жолдарын жасау және оларды пайдалану кезiнде мынадай жағдайлар анықталды:

-жол төсемесiнiң қабаттарында көлiктiң салмағы әсерiнен ығысу кернеулерi пайда болады;

-өте жоғары оң таңбалы температура әсерiнен асфальт-бетон қабаттардың ығысуға қарсыласу қабiлетi төмендеп, жиі қайталанатын жүктiк күштер оларда қалдық деформациялардың бiртiндеп жиналуына әкеліп соғады. Бұл жағдай ығысу, ағу және төсемедегi толқындар түріндегі деформациялардың пайда болуына әсер етеді;

-асфальт-бетон салқындаған кезде ол сығылады да, жамылғыда созушы кернеулер мен деформациялар пайда болады. Осының әсерiнен жамылғыны түгел кесiп өтетiн периодты тәртiппен орналасқан көлденең жарықшақтар пайда болады.

Демек, автомобиль жолдарының негiзгi элементтерiнiң бiрi - жол төсемесiнiң кернеулi-деформациялық жағдайы, оның берiктiгi мен жұмыс iстеу қабiлетiнiң ұзақтығы көптеген факторға байланысты екен. Бұл факторлар көлiк құралдарының статикалық және динамикалық әсерлерi, қоршаған ортаның температурасы, жол төсемесiнiң негiзiнiң ылғалдылығы және де көптеген жағдайлардан тұрады.

Жоғарыда аталып өткен мәселелер Қазақстан жағдайында, атап айтқанда, оның оңтүстiк-шығысы үшiн толық зерттелмегендiктен, дипломдық жұмыста қарастырылып отырған тақырып бүгiнгi таңда актуалды болып табылады.

Қазақстанның кең байтақ территориясының әрбiр аймағының ылғалдылық жағынан, қоршаған ортаның температурасы мен оның жыл кезеңдерiнде өзгеру режимi жағынан және тағы да басқа өзiндiк ерекшелiктерi мол болғандықтан бүкiл Қазақстан үшiн асфальт-бетон жамылғыларының есептеу температураларын анықтаудың бiрегей тәсiлiн табу бүгiнгi таңда көптеген қиындықтарға әкелiп соғатыны түсiнiктi. Сондықтан аталған мәселелер дипломдық жұмыста тек оңтүстiк-шығыс аймақ үшiн зерттеледі.

Қарастырылып отырған есептердi теориялық тәсiлдермен шешуге мүмкiндiк бар. Көп қабатты жол конструкциясының ерекшелiктерiн ескеруге соңғы кезде кеңiнен таралған шектi элементтер әдісін қолдануға болады. Ол үшiн, бiрiншiден, есептің арнайы жасалынған математикалық моделін құрып, оны аталған әдіспен компьютерде есептеу қажет. Екiншiден, жол төсемелерiнiң температуралық жағдайының жыл бойы өзгерiске ұшырау заңдылықтарын анықтау үшiн қоршаған ортаның температурасының өзгеру заңдылықтарын метеостанциялардың жинаған мәлiметтерi арқылы анықтау керек.

Дипломдық жұмыстың мақсаты Қазақстанның оңтүстiк-шығыс аймағындағы көпқабатты автомобиль жолдарының температуралық жағдайының жыл бойы өзгеру заңдылықтарын математикалық модельдеу арқылы жанжақты зерттеу.

Қойылған мақсатты орындау үшiн мынадай жұмыстар атқарылуы керек:

Қазақстанның оңтүстiк-шығыс аймағындағы қала сырты жолдарының көлденең қималары үшiн есептеу схемалары мен есептеу алгоритмдерiн жасау және есептеу алгоритмдерiн компьютер арқылы жүзеге асыру;
теориялық есептеулер арқылы жол конструкциясының температуралық

күйінің жыл бойы өзгеру заңдылықтарын анықтау;

- жүргiзiлген зерттеулердiң нәтижелерi негiзiнде жол конструкцияларының

температуралық жағдайын жолдарды жобалау кезiнде ескерудiң тәсiлдерi

туралы ұсыныстар жасау.

Жұмыста есептеу-теориялық тәсілін қолдану арқылы оңтүстiк-шығыс жолдарының температуралық жағдайының жыл мезгiлдерiне байланысты өзгеру механизмi зерттеледi. Арнайы құрылған есептеу алгоритмiн компьютерде жүзеге асыру арқылы алынған мәндердi Қазақстанның қалған жолдарының жылдың кез келген мерзiмдегi температуралық жағдайын аталған алгоритм арқылы анықтауға болады.

Дипломдық жұмыс кiрiспеден, екі тараудан тұратын негiзгi бөлiктен, қорытындыдан, пайдаланған әдебиеттер тiзiмiнен және қосымшалардан тұрады.

Бiрiншi тараудың басында шекті элементтер әдісін компьютерде жүзеге асыруда қолданылатын MATLAB жүйесіне шолу жасалынады. MATLAB жүйесінің өзіндік алгоримдік тілінің құрылымына, оның мүмкіндіктеріне сараптама жасалынған.

Осы тарауда сонымен қатар автомобиль жолдарының төсемелерiнiң температуралық режимiн шекті элементтер әдісімен анықтаудың теориялық негіздері келтірілген. Стационарлы температуралық режимнің жылу алмасу процесі арқылы қалыптасатынын айта келіп жылу алмасудың конвективті, кондуктивті және сәулелік түрлері бар екені айтылады және олардың әрқайсысына сипаттама беріледі. Математикалық физика теңдеулері пәнінде қарастырылатын жылу өткізгіштіктің негізгі теңдеуі келтіріліп, оны шешудің жолдары сарапталынады және теңдеуді шешуге қажетті бастапқы және шекаралық шарттардың түрлері талқыланады. Тұтас денелер үшін мұндай теңдеуді шешудің ең тиімді жолы ретінде шекті элементтер әдісін қолдану қажет екені негізделіп, аталған әдістің негізгі теңдеулер жүйесін құру жолдары келтіріледі.

Екінші тарауда автомобиль жолдарының көпқабатты құрылымының температуралық есебі қойылған. Қала сырты автомобиль жолдарының көлденең қимасының эскизі келтіріліп, ондағы шекаралық шарттар температуралық түрде берілген. Автомобиль жолдарының көп қабатты болатыны ескеріліп жол қабаттарының жылу-техникалық сипаттамалары келтірілген. Тереңдігі 10 м болатын қабатта температураның жыл бойы өзгермей тұрақты шамада болатыны айтылады және жол қимасының екі шетіндегі температура тереңдікке байланысты сызықтық тәуелділікпен өзгеретіні ескеріледі. Тараудың екінші жартысында компьютерде есептелінген жол қимасындағы температуралық өрістер жыл мезгілінің әртүрлі маусымдары үшін температуралық изотермалар түрінде келтірілген. Жылу өткізгіштіктің негізгі теңдеуі итерациялық, жоғарғы релакциялық Зейдель тәсілімен шешілгеннен кейін жол қимасындағы температуралық өріс сандық кесте түрінде алынып жұмыстың қосындысында кестелер түрінде беріледі. Алынған сандық нәтижені талдауға ыңғайлы болу үшін DELPHI тілінде арнайы “Изолиниялар” деп аталатын программа құрылған. Осы программаның көмегімен сандық нәтижелер изотермалар түрінде алынып, дипломдық жұмыстың екінші тарауының соңында келтірілген.

Дипломдық жұмыс аумағында мынадай нәтижелер алынған:

есептік тәжiрибелер негiзiнде қоршаған ортаның температурасы мен асфальт-бетон төсемесiнiң қабаттарының температураларының арасындағы байланыс анықталынған;
теориялық есептеу кезiнде қоршаған ортаның ауасы мен асфальт-бетон жамылғы бетiнiң арасындағы жылу алмасу процессi конвективтi түрде өтетiнi ескерiлiп, бұл жағдайдың асфальт-бетон төсеменiң жоғарғы қабаттарына ғана маңызы бар екенi анықталған.

I ТАРАУ. ҚАЛА СЫРТЫ ЖОЛДАРЫНЫҢ ТЕМПЕРАТУРАЛЫҚ ЖАҒДАЙЫН ШЕКТІ ЭЛЕМЕНТТЕР ӘДІСІМЕН MATLAB ЖҮЙЕСІНДЕ ЗЕРТТЕУДІҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ

1. 1. MATLAB жүйесіне кіріспе

MATLAB - матрицалық лаборатория - ғылыми-техникалық есептеулерге арналған ең үздік программалау жүйесінің бірі. Бұл жүйе қазіргі таңда есептеу математикасына, мәліметтерді өңдеуге, электрондық приборларды жобалауға, экономикаға және т. б. қолданбалы ғылым салаларына арналған бірнеше ондаған қосымшалармен толықтырылған.

MATLAB ең алдымен сандық алгоритмдерді программалауға арналған жүйе. Ол 1970 жылдары АҚШ-та жасалған қолданбалы LINPACK және EISPACK пакеттерінің негізінде пайда болды. MATLAB-тың пайда болуы қазіргі таңда үздік дамыған MathCad, MAPLE және Mathematica жүйелерінің өмірге келуіне себеп болды. MATLAB жүйесінің дамуына есептеу математикасының дамуы мен жеке компьютерлердің архитектурасының өзгерулері көп ықпал етті.

MATLAB - жоғары деңгейдегі программалау жүйесі. Оның құрамында барлық есептеулер түрлерін жүргізуге, мәліметтер қорымен жұмыс істеуге және ақпараттарды графикалық түрде өңдеуге арналған командалардың бай қоры бар. Бұл командалар жүйенің әртүрлі директорияларында орналасқан тақырыптық топтарға бөлінеді. Жүйеде 800-ге жуық командалар бар, олардың тең жартысына жуығы жүйемен жаңа танысып отырған қолданушыға түсінікті. Мүмкіндігі кеңірек командалар С тілінде жазылған. Бірақ, командалардың басым көпшілігі MATLAB жүйесінің тілінде. Сондықтан бұл жүйе қолданушы үшін әрқашан ашық. Жүйеде екі-, және үш өлшемді графиктермен жұмыс істеуге және жүйеде бар командаларды қолданып өз командаларын құруға зор мүмкіншілік бар. Сонымен қатар, С және Фортран тілінде жазылған программаларды MATLAB жүйесінде қолдануға болады.

Бұл жерде келтіріліп отырған мәліметтер жүйемен жаңадан танысуға және MATLAB жүйесінің мүмкіндіктерін зерттеуге арналған.

MATLAB жүйесін РС-де немесе Мас-та іске қосу үшін MATLAB-тың фирмалық суретін екі рет шертсе болғаны. MATLAB-ты UNIX жүйесінде іске қосу үшін операциялық жүйенің жұмыс терезесіндегі командалық қатарда matlab сөзін теру керек. MATLAB-тан шығу үшін командалар қатарында quit сөзін тереді.

MATLAB жүйесін игерудің ең оңай жолы - ол матрицалармен жұмыс істеуді үйрену. Себебі, MATLAB жүйесінің басқа жүйелерден негізгі ерекшелігі, бұл жүйеде барлық сандар әртүрлі реттегі матрицалар деп қарастырылады. Мысалы, тұрақты сан (1 1) өлшемді матрица деп, ал вектор бір бағанадан немесе бір қатардан тұратын матрица деп қарастырылады. Жалпы түрдегі матрица деп төртбұрышты сандар массивын алады. Жүйенің тағы бір ерекшелігі, басқа жүйелерде матрицаны сандар жинағы деп қарастыратын болса, мұнда матрицаларға жеке сан ретінде қарап, оларға арифметикалық операциялардың барлық түрлерін сан ретінде қолдана береді. Осы айтылғандарды ескеріп MATLAB жүйесінде қолданылатын операцияларды матрицалары енгізуден бастайық.

Матрицаны енгізудің бірнеше тәсілі бар:

элементтердің толық тізімін беру;
матрицаны сыртқы файлдардан көшіріп алу;
жүйеде бар арнайы функциялар арқылы матрицаны есептеп шығу;
өзіңіз құрған М-файлдағы функция арқылы матрицаны есептеп шығу.

Матрицаны тізіммен енгізу үшін мынадай негізгі ережелерді ұстану керек:

элементтер өзара бос орын немесе үтір арқылы бөлінеді;
әрбір қатардың соңы нүкте-үтірмен (; ) белгіленеді;
матрицаның барлық элементтері квадрат жақшамен ( [ ] ) қоршалады.

Мысалы, сиқырлы матрица деп аталатын мынадай сандар массивын енгізейік:

A=[16 3 2 13; 5 10 11 8; 9 6 7 12; 4 15 14 1] .

Енгізілген матрица автоматты түрде MATLAB ортасында сақталады да,

оны кез келген уақытта А түрінде шақырып алуға болады.

Бұл матрицаның ерекшелігі, матрицаның кезкелген бағаналарының немесе кезкелген қатарларының элементтерінің қосындылары бірдей және ол 34 санына тең. Сонымен қатар, оның диагоналдарында орналасқан элементтердің қосындысы да 34 санына таң.

MATLAB енгізілген матрицаны былайша түрлендіреді:

А=

16 3 2 13

5 10 11 8

9 6 7 12

4 15 14 1

Матрицаның бағаналарының элементтерінің қосындыларынан вектор-қатар құрайық. Ол үшін sum(A) командасын енгізсе жеткілікті. MATLAB мынадай нәтиже шығарады:

ans =

34 34 34 34

Егер алынатын нәтижеге алдынала арнайы идентификатор белгіленбесе, онда MATLAB оны автоматты түрде ans деп атап, келесі қатардан бастап нәтижені шығарып береді. Бұл жерде ans идентификаторы ansver -жауап деген сөзден қысқартылып алынған. MATLAB жүйесінде алдымен бағаналар қарастырылатын болғандықтан, берілген матрицаның қатарларының элементтерін есептеу үшін алдымен берілген матрицаны транспондап аламыз. Матрицаны транспондау апостроф белгісімен іске асады.

командасының көмегімен матрица транспондалады да, нәтижесі былайша басылып шығады:

ans =

16 5 9 4

3 10 6 15

2 11 7 14

13 8 12 1

Енді матрицаның қатарларының элементтерін есептеу үшін

Sum(A') '

командасын қолданамыз. Нәтижесі вектор-бағана ретінде алынады:

ans =

Матрицаның диагональдарының элементтерін есептеу үшін алдымен бас диагоналдың элементтерінен массив құрайық. Ол үшін diag командасын пайдаланамыз:

diag(A) =

Енді sum(diag(A) ) командасы диагоналдық элементтердің қосындысын береді:

ans =

34.

Осылайша біз матрицаларға қолданылатын бірнеше операцияларды игердік.

Енді MATLAB-та қолданылатын индекстермен танысайық. Матрицаның қатары i индексімен, бағанасы j индексімен жабдықталады да A(i, j) арқылы белгіленеді. Мысалы сиқырлы матрицаның төртінші бағанасының элементтерін есептеу үшін

A(1, 4) +A(2, 4) +A(3, 4) +A(4, 4)

командасын қолданып

ans=

мәнін аламыз. Бірақ бұл тәсіл тиімді емес. Мұндай жағдайда матрицаның бір ғана индексін өзгерту тәсілін пайдаланған жөн. Мысалы, A(1:k, j) операторы массивтың j -шы бағанасының элементтерін 1-ден k -ға дейін тізбектеп береді. Ал

sum(A(1:4, 4) )

командасы алдында қарастырылған төртінші бағананың элементерінің қосындысын есептеп береді. Бұл жерде қолданылған (:) -қос нүкте операциясының MATLAB жүйесіндегі маңызы зор. Мысалы, sum(A(:, end) ) командасы арқылы матрицаның соңғы бағанасының элементтерінің қосындысы алынады.

Басқа алгоритмдік тілдер сияқты нақты программа құру үшін MATLAB жүйесінде де математикалық сөйлемдер құрылады. Олардың құрамында

айнымалылар;
сандар;
операторлар;
функциялар

болады.

MATLAB жүйесінің тағы бір негізгі ерекшелігі ол айнымалылардың типін анықтауды қажет етпейді. Жаңадан кездескен айнымалыға MATLAB автоматты түрде өзінің жадынан орын бөледі, ал егер ол айнымалы бұрыннан бар болса, онда оның құрамын өзгертіп, қажет болса жадынан қосымша орын тағайындайды.

Айнымалылар әріптермен, цифрлармен және астын сызу символымен белгіленеді. MATLAB бас әріптермен кіші әріптерді бөліп қарайды. Мысалы, A мен a екі түрлі айнымалы.

MATLAB жүйесінде сандар ондық есептеу жүйесінде қарастырылады. Ондық дәреже e әріпімен көрсетіледі. Комплекс сандардың жорамал бөлігін белгілеуге i немесе j әріптері суффикс ретінде пайдаланылады. Төменде MATLAB жүйесінде сандардың дұрыс жазылуына мысалдар келтірілген:

3 -99 0. 0001

9. 6397238 1. 60210 e -20 6. 02252 e 23

1 i -3. 14159 j 3e5i .

Сандардың бәрі компьютердің жадында IEEE стандартымен анықталатын long форматымен сақталады. Жылжымалы нүктемен сипатталатын сандарда 16 мағыналы цифр болады да, олардың мәндері 10 ^-308 -ден 10 ³⁰⁸ -ге дейінгі диапазонда өзгереді.

MATLAB жүйесінде мынадай операторлар қолданылады:

+ қосу;

- алу;

* көбейту;

/ бөлу;

\ сол жақтан бөлу;

^ дәреже;

' дефис-транспондау белгісі;

() есептеу тәртібін көрсететін жақшалар.

MATLAB жүйесінде элементарлық математикалық функциялардың үлкен қоры бар. Мысалы, abs, sqrt, exp, sin және т. б. Жүйеде теріс сандардың квадрат түбірлері мен логарифдері де есептеліп, нетижесі комплкс сандар түрінде алынады. Сонымен қатар күрделі, Гамма функциясы мен Бессель функцияларының да стандартты командалары бар. Барлық математикалық функциялардың тізімін алу үшін

help elfun

командасын қолданса болғаны.

Бірнеше арнайы функциялар жиі қолданылатын константаларды береді:

pi 3. 14159265 . . .

i жорамал бірлік,

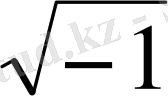
j мағынасы 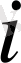-мен бірдей

eps жылжымалы нүктелі санның салыстырмалы дәлдігі, 2 ^-52

realmin ең кіші жылжымалы нүктелі сан, 2 ^-1022

realmax ең үлкен жылжымалы нүктелі сан, 2 ¹⁰²³

Inf шексіздік

NaN сан емес дегенді көрсетеді. Бұл белгі 0/0 немесе Inf-Inf операцияларының математикалық мағынасы жоқ екені туралы ескертеді.

Бұл функциялардың мағыналарын қажетінше өзгертіп отыруға болады. Мысалы

eps=1. e-6 .

Функцияның бастапқы мәніне қайта оралу үшін

clear eps

командасы орындалады.

Матрицалармен жұмыс істеу

Матрицаларды жүйенің көмегімен де құруға болады. Ол үшін

zeroбәрі ноль
onesбәрі бір саны
randкездейсоқ сандардың біркелкі таралуы
randnкездейсоқ сандардың нормальды таралуы

командалары қолданылады. Соңғы екі команда математикалық статистика есептерінде қолданылатын болғандықтан оларға арнайы тоқталу қажет. Ал алдыңғы екі команда сандық қатар элементтерін өзара қосу, немесе көбейту операцияларында нәтиже жинақталатын матрицаларды тазалап алу үшін қолданылады.

Мысалдар келтірейік:

Z=zero(2, 4)

0 0 0 0

F=5*ones(3, 3)

5 5 5

MATLAB жүйесінде сандардың массивынан тұратын матрица мәтіндік файл түрінде құрылады. Төртбұрышты кестенің элементтері өзара бос орын арқылы бөлінеді және матрицаның қатарларындағы элементтер саны бірдей болу керек. Мысалы MATLAB жүйесінің сыртында 4 қатардан тұратын мәтіндік файл құрайық:

16. 0 3. 0 2. 0 13. 0

5. 0 10. 0 11. 0 8. 0

9. 0 6. 0 7. 0 12. 0

4. 0 15. 0 14. 0 1. 0

Файлды magik. dat деген атпен сақтайық. Енді

load magik. dat

деген команда осы файлды оқып, берілген матрицадан тұратын magik деген айнымалыны құрады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.