Эксперимент берілістері бойынша объектілердің статикалық және динамикалық сипаттамаларын анықтау


ҚАЗАҚСТАН РЕСПУБЛИКАСЫ ҒЫЛЫМ ЖӘНЕ БІЛІМ МИНИСТРЛІГІ
Қ. И. Сәтбаев атындағы Қазақ ұлттық техникалық университеті
Технологиялық кешендердің электржетегі және автоматтандырылуы
кафедрасы
Курстық жобаға
ТҮСІНІКТЕМЕЛІК ЖАЗБА
Тақырыбы: Объектілердің статикалық және динамикалық сипаттамаларын эксперимент берілулері бойынша анықтау
Жетекші:
Малдыбаева Т. С.
“” 2006 ж.
Нормабақылаушы:
Ғ. П. Қалымбетов
“” 2006 ж.
Студент: Қошқарбаев Қ. С.
Мамандығы: 050718
Тобы: Ээб - 04 - 4к
Алматы 2006
ҚАЗАҚСТАН РЕСПУБЛИКАСЫ ҒЫЛЫМ ЖӘНЕ БІЛІМ МИНИСТРЛІГІ
Қ. И. Сәтбаев атындағы Қазақ ұлттық техникалық университеті
Автоматика және басқару институты
“Технологиялық кешендердің электржетегі және автоматтандырылуы”
кафедрасы
“БЕКІТЕМІН”
Кафедра меңгерушісі
тех. ғыл. докторы, профессор
А. Б. Бекбаев
“” 2006 ж.
Курстық жобаға
ТАПСЫРМА
Студент: Қошқарбаев Қ. С.
Жобаның тақырыбы: Объектілердің статикалық және динамикалық сипаттамаларын эксперимент берілулері бойынша анықтау
Аяқталған жобаны тапсыру мерзімі : 2006 ж
Жобаның бастапқы берілістері: вариант нөмірі - 23; .
.
.
Есептік түсініктемелік жазба мазмұны : .
.
.
Тапсырманың берілген күні : . 2006ж.
Кафедра меңгерушісі Бекбаев А. Б.
Жоба жетекшісі Малдыбаева Т. С.
Жобаны орындауға
алған студент Қошқарбаев Қ. С.
“ ” 2006 ж.
М а з м ұ н ы
К і р і с і п е . . . 2
1Сызықты объектілердің функционалды тәуелділіктерін ең кіші квадраттар әдісімен анықтау . . . 3
1. 1 Ең кіші квадраттар әдісі бойынша, cызықты объектілердің функционалды тәуелділігін анықтау . . . 3
1. 1. 1 Сызықты емес объектілердің функционалды тәуелділігін анықтау . . . 7
1. 1. 2 Бейсызықты объектінің статикалық сипаттамасын ең кіші квадраттар әдісімен түзету . . . 8
1. 2 Басқару объектілердің динамикалық сипаттамаларын екпін қисығы бойынша анықтау. . 11
1. 2. 1 Бірінші ретті динамикалық сипаттамаларын екпін қисығы бойынша анықтау . . . 12
1. 2. 2 Екінші ретті объектінің динамикалық сипаттамасын монотонды екпін қисығы бойынша анықтау15
1. 2. 3 Екінші ретті объектінің динамикалық сипаттамасын тербеліс екпін қисығы бойынша анықтау18
1. 3 Объектінің теңдеуін жиіліктік әдістер бойынша анықтау. . 20
1. 3. 1 Басқару объектісінің беріліс функциясын экспериментальды жиіліктік сипаттама бойынша анықтау20
1. 3. 2 Екпін қисығы бойынша кеңейтілген жиіліктік сипаттамасын алу………. . 23
Қорытынды. 30
Әдебиеттер тізімі 31
КіріспеҚазіргі кезде техника мен технологияның түрлі салаларында басқару процесіне жоғары талаптар қою - идентификацияның маңызды мәселелері болып табылады. Себебі, математикалық модель жеткілікті дәдігімен белгілі болмаса, жүйенің жоғары сапалы басқарылуын қастамассыз ету мүмкін емес.
Объектілердің динамикалық қасиеттерін зерттеу, детерминизмнің негізгі сұрақтарына жауап беру керек. Яғни, белгілі ықпал мен бастапқы кездегі белгілі координаттар бойынша кезекті уақытта координаттардың өзгеруін алдын ала болжау керек. Жүйенің анализі мен синтезін дамыту үшін басқару объектілері айнымлыларының өзара байланыс теңдеулерін білу қажет.
Объектілердің статика және динамика теңдеулері кіріс ықпалдың және шығыс координаттар арасындағы себеп - салдарлы тәуелділікті сипаттайды. Статика теңдеуі - динамика теңдеуінің жеке жағдайы болып табылады.
Кез келген технологиялық процесс, жеке типтік аппараттар түрінде орындалатын бірқатар операциялардан тұрады. Сондықтан, динамика анализі түрлі технологиялық процесстер үшін ортақ аппараттарды зерттеуден басталып, содан кейін спецификалық жағдайлар қарастырылады.
1 Объектілердің статикалық және динамикалық сипаттамаларын эксперимент берілулері бойынша анықтауЖобалау кезде нақты шешім үшін әріпті теңдеулер бағаланбайды. Жалпы әріпті теңдеу емес, нақты объектіге сәйкестігі бар сандық теңдеу болуы міндетті. Теориядан әрқашан сандық теңдеуді алу мүмкін емес. Осындай жағдайда эксперимент өткізеді, бұл кезде зерттелетін объектінің бір немесе бірнеше айнымалыларын немесе ауыспалы процестерін өлшеп тіркейді. Бұл процестер ізделетін дифферинциалды теңдеудің дербес шешіміне сәйкес келеді.
Өнеркәсіптік обьектілердің статикалық сипаттамаларын алу үшін активті эксперимент әдісін қолданады, егер объект активті ықпалды қолдану мүмкін болса, онда тік бұрышты толқын әдісін қолданады. Осы детерминистік әдістерден басқа, объектіге жасанды ықпал әсер етпейтін статистикалық динамика әдісіде қолданылады.
Айтылғандардың бәрінің сызықты объектіге қатысы бар. Сызықты емес объектілер үшін де, детерминистік және ықтималдық әдістерді қолдануға болады. Бірақ мұндағы әдістер әжептеуір қиын болатындықтан, әзірше практикалық түрде тек бірінші ретті объектілер үшін қолданылады. Барлық технологиялық жағдайларды қарастыру мүмкін емес, және ол керекте емес, өйткені әдістер белгілі динамикалық жүйелердің топтары үшін жалпы мінездеме береді. Әрі оларды қолдану, объектілердің физикалық табиғатына тәуелді емес. Днамиканың жалпы теңдеулерінің мәні: объектіні қандай да бір динамикалық класқа жатқызып, содан соң теңдеуді эспериментальды анықтайтын орынды әдісін таңдау.
Ескерте кету керек, бастапқы экспериментальды материалда өлшеу қателігі бар, өйткені ол оның қорытындысы болып табылады. Сондықтан эксперименттің тазалығы және дәлдігі өте қажет. Өлшеудің қателігі, оларды азайту әдісі, экспериментті жоспарлау, эксперименттің берілістердің нақтылығын жоғарылату мақсаты әдебиетте қарастырылған. Сондықтан, экспериментальды берілістерді өндеу әдістерін толығырақ қарастырамыз .
1. 1 Басқару объектілердің статикалық сипаттамаларын ең кіші квадраттар әдісімен түзету
Теңдеуді экспериментальды анықтау кезінде өлшемділік қате болады. Өлшеу процесі кезінде ол қатені жоюға тырысады, сонымен қатар қатені берілістерді жөндеу кезінде де азайтуға тырысады. Бұл жолдардың біреуі ККӘ болып табылады. Егер қателіктер қалыпты үлестірімге және статистикалы тәуелсіз болса (корреляциялы емес), әдіс - ықтималдық қортынды береді. Әдісті қолдану жағдайы, экспериментальды өлшемділіктер сандарының көптігіне байланысты. Егер бір белгісіз өлшенетін болса, онда бір эксперимент болу керек. Бірақ, бірнеше эксперимент жүргізіліп, қорытындылар орталанады. Бұл жағдайда орталау ККӘ-мен орындалады.
Айталық, белгісіз х мүшесін анықтау үшін n өлшем өткізіледі. Өлшемдердің берілістері: y 1 , y 2 , . . . , y n . y 1 -x, y 2 -x, …, y n - x айырымын және олардың квадратын ( y 1 -x) 2 , (y 2 -x) 2 , . . . , (y n - x) 2 құрастырамыз. х мұшесін, квадраттардың қосындысы минимальды болатындай таңдап, мынаны аламыз:
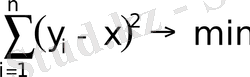 (1)
(1)
Осыған келесі шарт тура келеді:
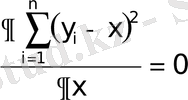 немесе
немесе
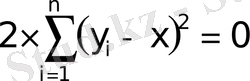 .
.
Бұдан алатынымыз:
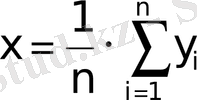 . (2)
. (2)
Егер кейбір өлшемдіктер нақты тең болмаса, онда келесі шаманы минимумдау керек:
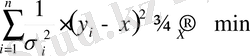 (3)
(3)
мұндағы
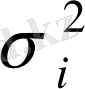 - жеке өлшемділік қателігі, дисперсиясы.
- жеке өлшемділік қателігі, дисперсиясы.
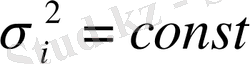 болғанда (1) - өрнекті аламыз.
болғанда (1) - өрнекті аламыз.
Бірнеше топтар арасындағы функциональдық тәуелдікті өлшеу кезінде, бұл әдіс өте қиын жолмен есептеледі. Ол үшін мысалдар қарастырылған.
1. 1. 1 сызықты объектінің статикалық сипаттамасын ең кіші квадраттар әдісімен түзету
1-кесте мен 1 а -суретте сызықты динамикалық жүйенің статикалық сипаттамасын экспериментальды анықтау берілістері келтірілген.
1-кесте
 x
і
= 27, 50
x
і
= 27, 50
 y
і
= 43, 20
y
і
= 43, 20
 x
і
2
= 96, 25
x
і
2
= 96, 25
 x
і
ƒy
і
= 131, 45
x
і
ƒy
і
= 131, 45
Енді ККӘ бойынша объектінің х кірісі мен у шығысы арасындағы статикалық тәуелділіктің шамасын табу керек.
Шешімі . Бастапқы тәуелділікті мына түрде жазамыз:
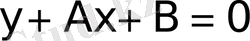 . (4)
. (4)
х і және y і - тің екі мәндерін алсақ жеткілікті, табылған екі теңдеуден А және В- ны табу керек. Бірақ оған басқа экспериментальды х і және y і шамаларын қойғанмен, теңдеуді қанағаттандырмайды:
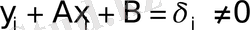 (5)
(5)
Алшақтықтар
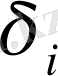 , геометриялық көзқараста (
х
і
, y
і
)
нүктелерінен алынған
у + Ах + В = 0
теңдеуімізге дейінгі аралыққа тең. Бұл түзуді, яғни оның
А
және
В
параметрлері, алшақтықтың орта мәні минимальді болатындай таңдап аламыз. Гаусстың ККӘ алшақтықтар квадратының қосындысы минимальді
, геометриялық көзқараста (
х
і
, y
і
)
нүктелерінен алынған
у + Ах + В = 0
теңдеуімізге дейінгі аралыққа тең. Бұл түзуді, яғни оның
А
және
В
параметрлері, алшақтықтың орта мәні минимальді болатындай таңдап аламыз. Гаусстың ККӘ алшақтықтар квадратының қосындысы минимальді
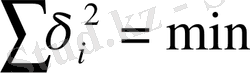 болатындай түзу жүргізеді.
болатындай түзу жүргізеді.
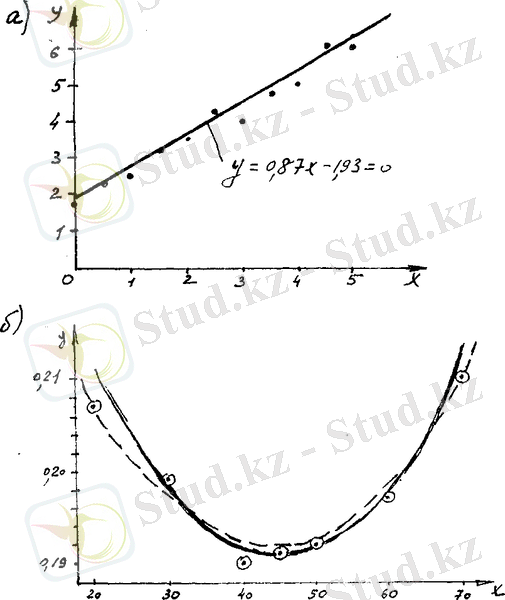
1-сурет. Сызықтық (а) және сызықсыз (б) тәуелділікті тегістеу
Әдісті қолданған жағдайда
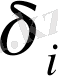 Equation. 3 кездейсоқ шама деп ал, заңы үлестірім нормальды деп аламыз. Айталық, бірдей шартта
х
і
және
y
і
шамаларын өлшегенде (4) үшін алынған келесі алшақтықтар
Equation. 3 кездейсоқ шама деп ал, заңы үлестірім нормальды деп аламыз. Айталық, бірдей шартта
х
і
және
y
і
шамаларын өлшегенде (4) үшін алынған келесі алшақтықтар
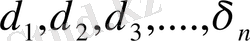 Equation. 3 болсын.
Equation. 3 болсын.
Бір-бірімен байланысы жоқ тәуелсіз алшақтықтардың бірлестік ықтималдықта пайда болуы, ықтималдықтардың көбейтіндісіне тең:
 Equation. 3 (6)
Equation. 3 (6)
А және В константалардың мәндері ықтималды, ал егер бұл шама ең үлкен болса, ол келесі жағдайда орындалады:
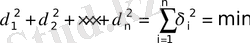 Equation. 3 . (7)
Equation. 3 . (7)
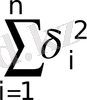 Equation. 3 минимумі квадраттық орта алшақтықтың минимумін береді:
Equation. 3 минимумі квадраттық орта алшақтықтың минимумін береді:
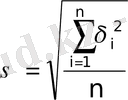
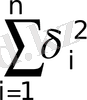 минимумін алу үшін
А
мен
В
қалай таңдап алу керек? Эстремум бар болудың қажетті шартын анықтайтын теңдеулер, ең негізі болып табылады:
минимумін алу үшін
А
мен
В
қалай таңдап алу керек? Эстремум бар болудың қажетті шартын анықтайтын теңдеулер, ең негізі болып табылады:
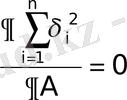 және
және
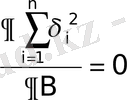 . (8)
. (8)
Оларды алу үшін, эксперименттен алынған мәндерден теңдеулердің шартты жүйесін құрады:
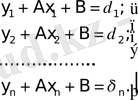 (9)
(9)
Әр шартты теңдеуді квадрат дәрежеге шығарады:
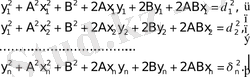 (10)
(10)
Бұлардың бәрін қосамыз:
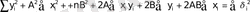 . (11)
. (11)
Бұдан екі нормаль теңдеуін табады:
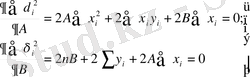 (12)
(12)
немесе:
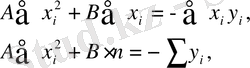
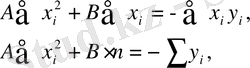
бұл жерден А мен В ықтималдық мәндерін есептейді.
Қарастырылып отырған сандық мысал үшін:
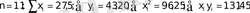 сандары 1-кестеде есептелінген. Берілген мысал үшін нормаль теңдеулер мына түрде болады:
сандары 1-кестеде есептелінген. Берілген мысал үшін нормаль теңдеулер мына түрде болады:
96, 25ƒA + 27, 5ƒВ = -131, 45.
27, 5ƒA + 11ƒB = -43, 20.
Бұдан:

Ізделген орталанған теңдеу мына түрге келді:
y - 0, 87ƒx - 1, 93 = 0.
1. 1. 2 Бейсызықты объектінің статикалық сипаттамасын ең кіші квадраттар әдісімен түзету
2-кесте мен 1 б -суретінде сызықтық емес объектінің статистикалық сипаттамасын анықтайтын эксперименттің қорытындысы келтірілген.
2-кесте
Ең кіші квадраттар әдісі бойынша объектінің кірісі - х және шығысы - y арасындағы аналитикалық тәуелділікті анықтау керек.
Шешімі . Алдымен аналитикалық тәуелділіктің түрін анықтау керек. Экспериментальдық берулілер бойынша (1 б- сурет) алынған нүтелерді параболамен тегістеуге болады:
y = A + Bx + Cx 2 . (13)
Мұндағы мақсат - А, В, С константалардың ықтималдық мәндерін анықтау.
Бірінші қадамда А’, В’, С’ жуық шамалар анықталады. Бұл үшін үш кез келген экспериментальды нүктелерді алып, олардың координаталарын бастапқы теңдеуге үш рет қоямыз. Бұл бізге үш теңдеуді береді, одан жуық А’, В’, С’ мәндері анықталады. Кіріс өзгерісінің берілген аралығынан бірқалыпты үлестірілген нүтелерді алған жөн. А’, В’, С’ тауып, ең кіші квадраттар әдісі бойынша коэффицеттердің түзетулерін табамыз.
А’, В’, С’ анықтау үшін 2-кестеден бастапқы параболаның контурын дәлдірек бейімділейтін, 1, 4 және 7 нүтелерді аламыз. Одан мына теңдеулерді аламыз:
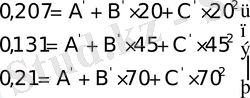 (14)
(14)
(14) -тен
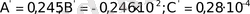 есептейміз. Енді түзетулерді қарастырамыз:
есептейміз. Енді түзетулерді қарастырамыз:
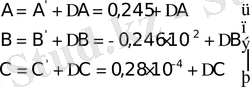 (15)
(15)
Енді
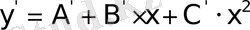 жуық параболадан экспериментальды нүкте ординаталарының ауытқуын табамыз. Ол үшін параболаның теңдеуіне
х
і
экспериментальды берілулеріне сәйкес келетін
x
1
=20; x
2
=30; …. ; x
7
=70
мәндерін қоямыз:
жуық параболадан экспериментальды нүкте ординаталарының ауытқуын табамыз. Ол үшін параболаның теңдеуіне
х
і
экспериментальды берілулеріне сәйкес келетін
x
1
=20; x
2
=30; …. ; x
7
=70
мәндерін қоямыз:
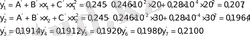
Сәйкес келетін экспериментальды у і шамалардан, табылған сандарды алып тастап, мынаны аламыз:
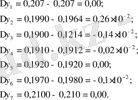
 ,
,
 ,
,
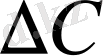 түзетулерді төмендегідей анықталады.
түзетулерді төмендегідей анықталады.
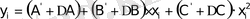 теңдеуіне
теңдеуіне
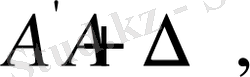

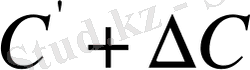 қойып одан,
қойып одан,
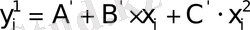 теңдеуін алып, түзетулерді есептеуге қажет теңдеуді аламыз:
теңдеуін алып, түзетулерді есептеуге қажет теңдеуді аламыз:
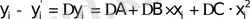
немесе сандық түрде:
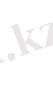
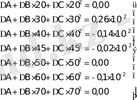 (16)
(16)
Бұл жүйеде, белгісіз мүшелердің санына қарағанда, теңдеулердің саны көп. Енді
 А,
А,
 В
және
В
және
 С
ықтимал мәндерін есептеу үшін ЕККӘ қолдану керек. Ол үшін барлық теңдеулерді квадраттап қосып, содан кейін:
С
ықтимал мәндерін есептеу үшін ЕККӘ қолдану керек. Ол үшін барлық теңдеулерді квадраттап қосып, содан кейін:
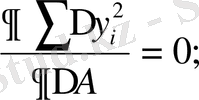
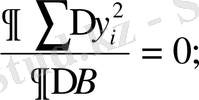
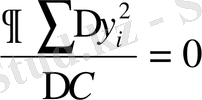 (17)
(17)
шарттан
 А,
А,
 В
және
В
және
 С
есептеп шығару үшін үш нормаль теңдеуді алу керек. Шартты жүйені нормаль түрге тез түрлендіруді келесі ереже бойынша жүргізуге болады:
С
есептеп шығару үшін үш нормаль теңдеуді алу керек. Шартты жүйені нормаль түрге тез түрлендіруді келесі ереже бойынша жүргізуге болады:
- бірінші нормаль теңдеуді құру үшін, осы теңдеудегі бірінші тұрған белгісіздің коэффициентіне әрбір шартты теңдеуді көбейтіп алынған теңдеулерді қосу керек;
- екінші нормаль теңдеуді құру үшін, осы теңдеудегі екінші тұрған белгісіздің коэффициентіне әрбір шартты теңдеуді көбейтіп барлық алынған теңдеуді қосу керек. Сол сияқты ары қарай жүре береді. Қанша белгісіздік болса, сонша нормаль теңдеу алынады. Бұл ережені 1-мысал үшін де қолдануға болады. (16) барлық теңдеуінде коэффициенті 1-ге тең болғандықтан, бірінші нормаль теңдеуді алу үшін, теңдеулерді қоссақ жеткілікті:
 Aƒ7+
Aƒ7+
 Bƒ315+
Bƒ315+
 Cƒ15925=0, 00.
Cƒ15925=0, 00.
Екінші нормаль теңдеуді алу үшін, мыналарды қосу қажет:

Бұдан алатынымыз:
 Equation. 3 Aƒ315+
Equation. 3 Aƒ315+
 Equation. 3 Bƒ15925+
Equation. 3 Bƒ15925+
 Equation. 3 Cƒ874125=-4, 7ƒ10
-2
.
Equation. 3 Cƒ874125=-4, 7ƒ10
-2
.
Үшін нормаль теңдеуді алу үшін тағы да мыналарды қосу қажет:
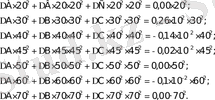
Бұдан аламыз:
 Equation. 3 Aƒ15925+
Equation. 3 Aƒ15925+
 Equation. 3 Bƒ874125+
Equation. 3 Bƒ874125+
 Equation. 3 Cƒ50850625=-3, 905.
Equation. 3 Cƒ50850625=-3, 905.
Табылған үш нормаль теңдеуден:
 Equation. 3 Aƒ7+
Equation. 3 Aƒ7+
 Equation. 3 Bƒ315+
Equation. 3 Bƒ315+
 Equation. 3 Cƒ15925=0, 00;
Equation. 3 Cƒ15925=0, 00;
 Equation. 3 Aƒ315+
Equation. 3 Aƒ315+
 Equation. 3 Bƒ15925+
Equation. 3 Bƒ15925+
 Equation. 3 Cƒ874125=-4, 7ƒ10
-2
;
Equation. 3 Cƒ874125=-4, 7ƒ10
-2
;
 Equation. 3 Aƒ15925+
Equation. 3 Aƒ15925+
 Equation. 3 Bƒ874125+
Equation. 3 Bƒ874125+
 Equation. 3 Cƒ50850625=-3, 905;
Equation. 3 Cƒ50850625=-3, 905;
түзетулер есептелінеді:

Алдында жуық есептеген параболаның параметрлеріне (15) түзетулерді енгізе отырып, мынаны аламыз:

Бұл кезде орталанған параболаның теңдеуі мына түрге келтіріледі:
y = 0, 2583 - 0, 2681ƒ10 2 ƒx + 0, 2873ƒ10 -4 ƒx 2 (18)
1. 2 Басқару объектілердің динамикалық сипаттамаларын екпін қисығы бойынша анықтау
Объектілердің теңдеулерін алу үшін, бір немесе бірнеше ауыспалы процестерді өлшеу және реттеу мақсатында эксперимент өткізеді. Бұл процестер ізделген дифференциалды теңдеудің дербес шешіміне сәйкес келеді.
Техникалық жүйелерде эксперименттің екі түрі кең қолданылады: екпін қисығы және жиіліктік сипаттамаларды алу. Бірінші жағдайда ізделіп отырған теңдеудің дербес шешімі, кіріс шама стандартты сатылы өзгеру кезіндегі, объектінің реакциясы болып табылады. Осы реакциядан объектінің теңдеуі табылады.
Екінші жағдайда, бір шешім емес, бірнеше шешім тіркеледі. Бұл шешімдер - түрлі белгіленген жиіліктер кезінде кіріс шаманың периодтық тербелістерінен амалсыз пайда болатын, объектінің шығыс шамасының тұрақталған тербелістері. Бұл дербес шешімдер - объектінің жиіліктік сипаттамалары - теңдеуді табу үшін қажетті алғашқы материал. Егер объектіде активті экспериментті қолдануға мүмкін болмаса, онда объектіге жасанды әсерді пайдаланбай, статистикалық динамиканың әдістерін қолданады.
Келесі сызықты дифференциалды теңдеу үшін:
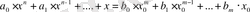 (19)
(19)
(мұнда n>m ; x, x 0 - объектінің кірісі мен шығысы)
нөлдік бастапқы шама кезінде және кірісі x 0 секірме түрде өзгерген кезде, шешімді уақыт функциясы мен коэффициенттер арқылы жазуға болады:
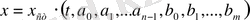 . (20)
. (20)
Керісінше, егер (19) объект теңдеуінің реті белгілі болып, кірісі сатылы түрде өзерген кезде, эксперимент арқылы екпін
x
ст
(t)
алынса, онда (19) теңдеуіндегі
a
і
, b
і
коэффициенттерін есептеуге болады (олардың саны
 ) . Ол үшін,
a
і
мен
b
і
коэффициенттері бар аналитикалық
x(t)
шешіммен (20), түрлі уақыт
t=t
і
(і=1, 2, …,
) . Ол үшін,
a
і
мен
b
і
коэффициенттері бар аналитикалық
x(t)
шешіммен (20), түрлі уақыт
t=t
і
(і=1, 2, …,
 )
кезіндегі
x’
ст
(t)
ықпал теңестіріледі. Нәтижеде,
a
і
, b
і
коэффициенттері бар
)
кезіндегі
x’
ст
(t)
ықпал теңестіріледі. Нәтижеде,
a
і
, b
і
коэффициенттері бар
 теңдеуден тұратын жүйе аламыз:
теңдеуден тұратын жүйе аламыз:
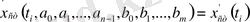 ,
,
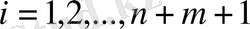 . (21)
. (21)
Бұл жүйеден, коэффициенттерді есептейді. Сонымен, екпін қисығының
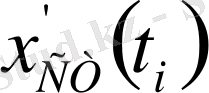 дискрет ординаты бойынша белгісіз
дискрет ординаты бойынша белгісіз
 коэффициентті анықтауға болады. Бұл идеяның түрлі вариациясы болуы мүмкін. Мысалы, басқа түрге ие ықпалды қолдану. Немесе, артық ординат санын алып, ең кіші квадраттар әдісін қолдануға болады.
коэффициентті анықтауға болады. Бұл идеяның түрлі вариациясы болуы мүмкін. Мысалы, басқа түрге ие ықпалды қолдану. Немесе, артық ординат санын алып, ең кіші квадраттар әдісін қолдануға болады.
Бізге тек қана (19) обьект теңдеуінің ретін білу қажет. (20) шешімдердің аналитикалық түрлері теңдеу ретіне байланысты әртүрлі болды. Егер теңдеудің қабылданған
n
реті, нақты реттен аз болса, онда аналитикалық шешімнің ординатасы мен “экспериментальды шешімді” теңестіру әдісі дұрыс емес -
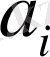 ,
,
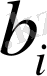 коэффициенттерін береді. Егер
коэффициенттерін береді. Егер
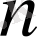 үлкен болып алынса, онда ол қауіпті емес, өйткені артық коэффициенттер нөлге тең болады.
үлкен болып алынса, онда ол қауіпті емес, өйткені артық коэффициенттер нөлге тең болады.
1. 2. 1 Бірінші ретті объектінің динамикалық сипаттамасын екпін қисығы бойынша анықтау
2-сурет. Екпін қисығы бойынша бірінші ретті обьектінің теңдеуін анықтау үшін
t
0
=0
тең уақыт кезінде кіріс
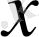 шаманы секірме түрде
шаманы секірме түрде
 бірлікке өзгертеміз. Санды түрде объект теңдеуін жазу қажет.
бірлікке өзгертеміз. Санды түрде объект теңдеуін жазу қажет.
Ізделген теңдеу төмендегідей болады:
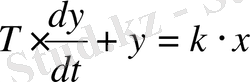 . 3 немесе
. 3 немесе
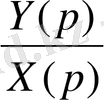 . 3=
. 3=
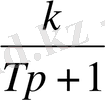 . 3. (22)
. 3. (22)
 мен
мен
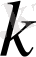 тұрақтыларын анықтау керек.
тұрақтыларын анықтау керек.
Алдымен берілген шарт кезіндегі теңдеу шешімінің аналитикалық өрнегін табамыз. Бұл шешімге
 мен
мен
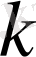 тұрақтылары кіреді. Алынған екпін қисығы графикалық шешім болғандықтан, графикті аналитикалық шешіммен салыстыра отырып, аналитикалық өрнектің тұрақтыларын табымыз.
тұрақтылары кіреді. Алынған екпін қисығы графикалық шешім болғандықтан, графикті аналитикалық шешіммен салыстыра отырып, аналитикалық өрнектің тұрақтыларын табымыз.
t=0 тең кездегі y=0 шарты үшін және t>0 болғанда, x=a шарты үшін, шешімнің жалпы түрі келесідей:
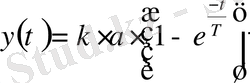 . (23)
. (23)
Графиктен екі нүктені алған жеткілікті. Содан соң, нүктелердің координаттарын шешімге қоя отырып, алынған екі теңдеуден
 мен
мен
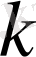 есептеуге болады. Бірақ, бұл теңдеулер трансцендентті:
есептеуге болады. Бірақ, бұл теңдеулер трансцендентті:
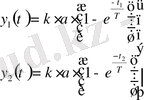 (24)
(24)
және олардың
 және
және
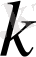 түбірлерін есептеу өте қиын. Сондықтан, келесі тәсілді қолдануға болады.
түбірлерін есептеу өте қиын. Сондықтан, келесі тәсілді қолдануға болады.
 кезінде
кезінде
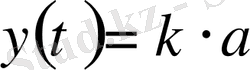 , демек, асимптота ординаты арқылы
, демек, асимптота ординаты арқылы
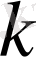 анықтауға болады:
анықтауға болады:
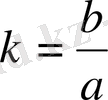 . (25)
. (25)
 анықтау үшін, шешімді дифференциялдаймыз:
анықтау үшін, шешімді дифференциялдаймыз:
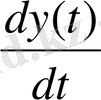 =
=
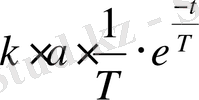
және
 ұмтылады:
ұмтылады:
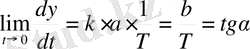 . (26)
. (26)
мұндағы
 -
-
 кездегі
кездегі
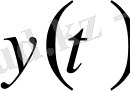 графигіне жүргізілген жанама сызықтың көлбеу бұрышы. Сондықтан:
графигіне жүргізілген жанама сызықтың көлбеу бұрышы. Сондықтан:
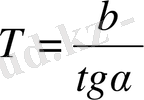 . (27)
. (27)
Сонымен
 саны, координат басынан асимптотамен қиылысқан нүктеге дейін, жанама сызық астындағы сызықтың ұзындығына тең. Бұл шешім ең қарапайым, бірақ дәл емес, өйткені жанама сызықты дәл жүргізу өте қиын әрі асимптотаның
саны, координат басынан асимптотамен қиылысқан нүктеге дейін, жанама сызық астындағы сызықтың ұзындығына тең. Бұл шешім ең қарапайым, бірақ дәл емес, өйткені жанама сызықты дәл жүргізу өте қиын әрі асимптотаның
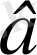 ординатын дәл белгілеу қиын. Бұл шешім кезінде графиктің басы мен аяғы ғана қолданылып, ал оның аралық нүктелері қарастырылмайды.
ординатын дәл белгілеу қиын. Бұл шешім кезінде графиктің басы мен аяғы ғана қолданылып, ал оның аралық нүктелері қарастырылмайды.
Енді дәлірек тәсілді қарастырамыз. Графикті бірдей ∆t аралық қашықтықтағы y 0 , y 1 , y 2 , … ординаталармен бөлеміз. Бұл нүктелер үшін теңдеудің шешімі бойынша мынаны жазуға болады:
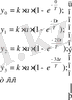 (28)
(28)
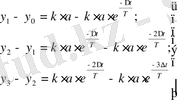 (29)
(29)
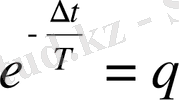 тең деп белгілейміз, онда:
тең деп белгілейміз, онда:
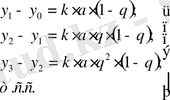 (30)
(30)
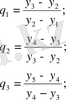 (31)
(31)
q 1 =1, 11; q 2 =0, 65; q 3 =0, 92.
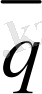 =(q
1
+q
2
+q
3
) /3=0, 61
=(q
1
+q
2
+q
3
) /3=0, 61
 санының бір-бірінен айырмашылығы - экспериментальды өлшеу мен
санының бір-бірінен айырмашылығы - экспериментальды өлшеу мен
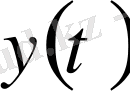
 тіркеудің қателігіне байланысты. Бөлек
тіркеудің қателігіне байланысты. Бөлек
 -дің орта арифметикалық
-дің орта арифметикалық
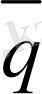 мәні - дәлірек орта мәнді береді. Содан соң, дәлденген уақыт тұрақтылығы
мәні - дәлірек орта мәнді береді. Содан соң, дәлденген уақыт тұрақтылығы
 мына өрнектен анықталады:
мына өрнектен анықталады:
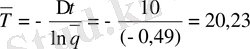 . (32)
. (32)
Сол сияқты белгілі
 бойынша
бойынша
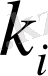 анықталады:
анықталады:
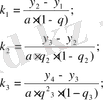 (33)
(33)
.
Содан кейін
k
1
, k
2
, k
3
, …-
терден орта арифметикалық
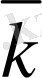 табылады. k
1
=-0, 0016; k
2
=0, 00088; k
3
=0, 0019;
табылады. k
1
=-0, 0016; k
2
=0, 00088; k
3
=0, 0019;
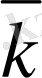 =0, 00039
=0, 00039
1. 2. 2 Екінші ретті объектінің динамикалық сипаттамасын монотонды екпін қисығы бойынша анықтау
3-суретте екінші ретті теңдеумен суреттелетін обьектінің екпін қисығы берілген:
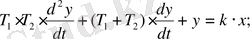 (34)
(34)
3-сурет. Бірқалыпты екпін қисығына ие екінші ретті обьектінің теңдеуін анықтау
Кірісіндегі сатылы әсер
 тең. Егер
t>0
кезінде кірісіндегі қобалжу бірлікке
тең. Егер
t>0
кезінде кірісіндегі қобалжу бірлікке
 тең екені белгілі болса,
Т
1
, Т
2
,
тең екені белгілі болса,
Т
1
, Т
2
,
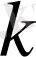 тұрақтыларын есептейміз.
тұрақтыларын есептейміз.
Жоғарыда қарастырылған жағдай сияқты, алдымен теңдеудің шешімін жалпы түрде жазу қажет:
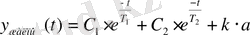 . (35)
. (35)
Содан соң бастапқы шарттардан,
t=0
болғанда
,
 ;
;
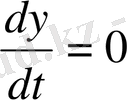 еркін тұрақтыларды анықтайды:
еркін тұрақтыларды анықтайды:
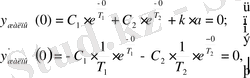 (36)
(36)
Бұлардан:
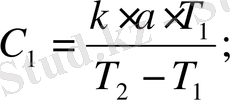
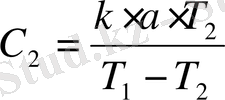 . (37)
. (37)
Ізделген дербес шешімді келесі түрде аламыз:
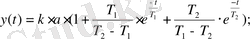 (38)
(38)
Енді берілген графиктен үш нүктенің
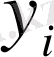 ,
,
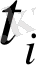 координаталарын алып, оларды үш рет теңдеуге қойып және осы тәсілмен алынған үш теңдеуден
координаталарын алып, оларды үш рет теңдеуге қойып және осы тәсілмен алынған үш теңдеуден
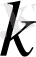 ,
,
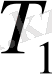 ,
,
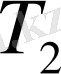 түбірлерін табуға болады. Бірақ бұл теңдеулер трансцендентті болғандықтан, түбірлерді есептеп табу өте қиын. Сондықтан А. Н. Крыловтың әдісін қолдану оңай .
түбірлерін табуға болады. Бірақ бұл теңдеулер трансцендентті болғандықтан, түбірлерді есептеп табу өте қиын. Сондықтан А. Н. Крыловтың әдісін қолдану оңай .
Ол үшін графикті бірдей
 аралық қашықтықтағы
аралық қашықтықтағы
 ,
,
 ,
,
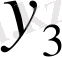 ,
,
 ординаталармен бөлеміз де, мына түрде жазамыз:
ординаталармен бөлеміз де, мына түрде жазамыз:
 (39)
(39)
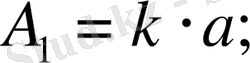
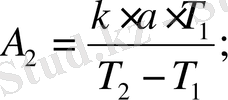
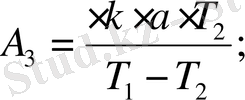
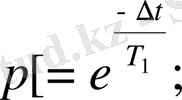
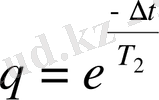 -деп белгілеп, өрнектерді төмендегі түрде жазамыз:
-деп белгілеп, өрнектерді төмендегі түрде жазамыз:
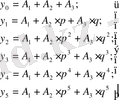 (40)
(40)
1,
 және
және
 сандарды кубтық теңдеудің:
сандарды кубтық теңдеудің:
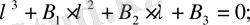 (41)
(41)
түбірлері деп есептейміз.
Бірінші жолды
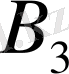 -ке, екінші жолды
-ке, екінші жолды
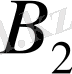 -ге, үшінші жолды
-ге, үшінші жолды
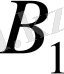 -ге, төртінші жолды 1-ге көбейтіп, оларды қосамыз. Бұл жағдайда, оң жақтағы бөлшектердің қосындысы нөлге тең болатындықтан:
-ге, төртінші жолды 1-ге көбейтіп, оларды қосамыз. Бұл жағдайда, оң жақтағы бөлшектердің қосындысы нөлге тең болатындықтан:
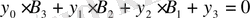 . (42)
. (42)
Сол операцияларды келесі төрт жолға қайта жасағанда:
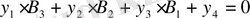 ; (43)
; (43)
Келесі төрт жолдан:
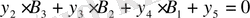 . (44)
. (44)
Осы үш теңдіктердегі
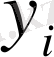 ординаталар екпін қисығынан белгілі, ал
ординаталар екпін қисығынан белгілі, ал
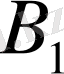 ,
,
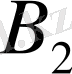 ,
,
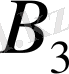 тұрақтыларды анықтау керек. Оларды анықтаған соң, кубтық теңдеудің түбірлерін есептеу керек:
тұрақтыларды анықтау керек. Оларды анықтаған соң, кубтық теңдеудің түбірлерін есептеу керек:
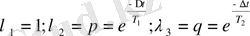 ; (45)
; (45)
Содан соң:
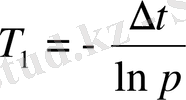 және
және
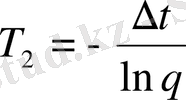 . (46)
. (46)
(40) жүйенің кез келген теңдеуінен (бірінші теңдеуден басқа),
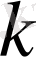 есептеу қажет. Дәлдікті көтеру үшін, алты бастапқы ордината емес, одан көп ординатаны алып, нәтижені орталандыруға болады. Бұл әдісте, берліген график, экспоненциалдық мүшелердің қосындысы арқылы жуықталады.
есептеу қажет. Дәлдікті көтеру үшін, алты бастапқы ордината емес, одан көп ординатаны алып, нәтижені орталандыруға болады. Бұл әдісте, берліген график, экспоненциалдық мүшелердің қосындысы арқылы жуықталады.
Енді сандық мысалды қарастырамыз.
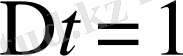 деп алып, екпін қисығынан (3-сурет) алты ординатаны өлшейміз (3-кесте) .
деп алып, екпін қисығынан (3-сурет) алты ординатаны өлшейміз (3-кесте) .
3-кесте
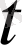
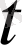 , с
, с
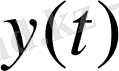

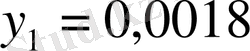
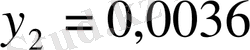
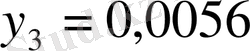
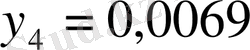
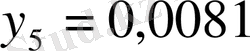
Теңдеулерден:
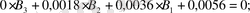
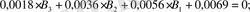
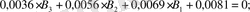
есептейміз:
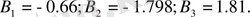
Кубтық теңдеудің түбірлерін табамыз:

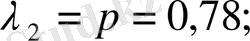
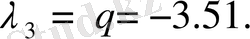
Содан соң:
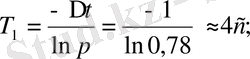
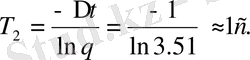
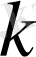 - ны есептеу үшін (2. 42) жүйедегі екінші жолды аламыз:
- ны есептеу үшін (2. 42) жүйедегі екінші жолды аламыз:
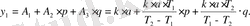
Сандарды қойған соң, мынаны аламыз:
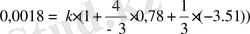 . 3
. 3
бұдан:
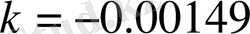 . 3;
. 3;
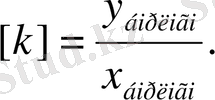 . 3
. 3
1. 2. 3 Екінші ретті объектінің динамикалық сипаттамасын тербеліс екпін қисығы бойынша анықтау
 кіріс шама сатылы түрде өзгерген кездегі (
кіріс шама сатылы түрде өзгерген кездегі (
 -дан
-дан
 -дейін,
м/мин
), шығыс ∆
-дейін,
м/мин
), шығыс ∆
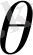 (t) реакциясынан объектінің теңдеуін табамыз (4-сурет) ;
(t) реакциясынан объектінің теңдеуін табамыз (4-сурет) ;
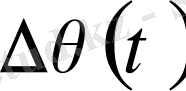 - температураның айырымы,
- температураның айырымы,
 - таспаның жылжу жылдамдығы.
- таспаның жылжу жылдамдығы.
Екпін қисығы тербеліс түрде болғандықтан, ізделіп отырған теңдеуді комплексті түбірлерге ие екінші ретті теңдеу деп алуға болады:
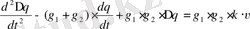 ; (47)
; (47)
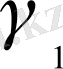 ,
,
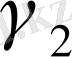 ,
,
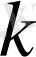 тұрақтыларды есептеу қажет. Бұл теңдеу жоғарыдағы теңдеу сияқты. Тек қана тұрақтылардың белгілеуі өзгертілген:
тұрақтыларды есептеу қажет. Бұл теңдеу жоғарыдағы теңдеу сияқты. Тек қана тұрақтылардың белгілеуі өзгертілген:
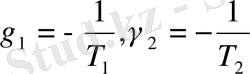 .
.

4-сурет. Тербеліс екпін қисығына ие е інші ретті объектінің теңдеуін анықтау
Тербеліс жүйенің теңдеуі әдетте мына түрде жазылады:
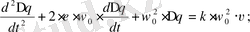 (48)
(48)
мұнда
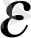 - демпфинг (азайту) коэффициенті;
- демпфинг (азайту) коэффициенті;
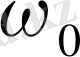 - жүйенің өзіндік жиілігі.
- жүйенің өзіндік жиілігі.
(47) және (48) теңдеулерден физикалық
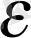 ,
,
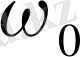 тұрақтыларымен
тұрақтыларымен
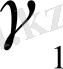 ,
,
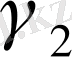 сандар арасындағы байланысты көреміз.
сандар арасындағы байланысты көреміз.
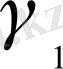 мен
мен
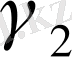 есептеуді оңайлату үшін енгізілген.
есептеуді оңайлату үшін енгізілген.
Жоғарыда алынған нәтижені қолданып, теңдеудің шешімін жазамыз:
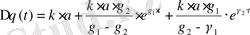 .
.
Басқару объектісі - тербеліс қасиеттерге ие болғандықтан, тұрақтыларды есептегенде нақты сан емес, комплексті санды аламыз:
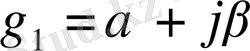 ;
;
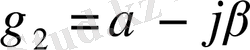 . (49)
. (49)
Эйлер формуласын (
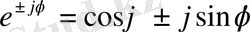 ) қолданып, (49) шешімді келесі түрде жазамыз:
) қолданып, (49) шешімді келесі түрде жазамыз:

 (50)
(50)
(50) теңдеуі екі гармониканың қосындысына сәйкес.
Екпін қисығынан бірдей
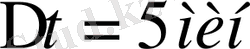 аралық қашықтықтағы алты ординатаны аламыз:
аралық қашықтықтағы алты ординатаны аламыз:
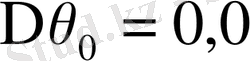 ;
;
 ;
;
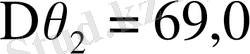 ;
;
 ;
;
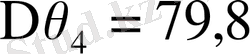 ;
;
 .
.
Кубтық (41) теңдеудің коэффициенттерін табу үшін теңдеулер жүйесін құрастырамыз:
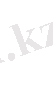
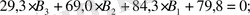
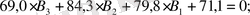
Бұдан:
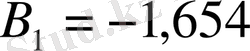 ;
;
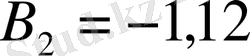 ;
;
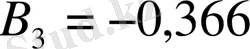 және келесі кубтық теңдеуді аламыз:
және келесі кубтық теңдеуді аламыз:
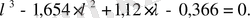
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz