Оптимизация әдістері: көп өлшемді оптимизация және симплекс әдісі


Қазақстан Республикасы Білім және ғылым министрлігі
Қ. И. Сәтбаев атындағы Қазақ ұлттық техникалық университеті
Электржетегі және технологиялық кешендерді автоматтандыру кафедрасы
Реферат
Оптимизация әдістері: көп өлшемді оптимизация.
Симплекс әдісі
Орындаған: ЭЭб-04-3к тобының студенті
Күзембаев Бақытжан ,
Қабылдаған: Сұлтанбекова Ж. Ж. ,
аға оқытушы
Алматы -2005
Мазмұны
Кіріспе . . . 3
- Оптимизацияның негізгі ұғымдары . . . 4
- Оптимизацияның көп өлшемді есептері . . . 5
- Симплекс әдісі . . . 12
Қолданылған әдебиеттер тізімі . . . 15
Кіріспе
ХХ ғасырдың орта шенінде атом энергиясын игерудің күрделі жұмыстарына байланысты алғашқы электрондық машиналардың пайда болуы және оларды ары қарай жетілдіру ғылым мен техника саласында революциялық өзгерістер жасады. Ғылымда зерттеу жұмыстарының әдістері күрт өзгеріп, күрделі құбылыстарды зерттеу мен болжау мүмкіндіктері жаңа деңгейге көтерілді. Соның нәтижесінде ғасырлар бойы шешілмей келген ірі ғылыми-техникалық проблемалар өз шешулерін тапты. Ғарышты, атом энергиясын игерудегі жетістіктер электроника мен информатика саласындағы табыстармен тікелей байланысты. Бүгінгі есептеу техникасы күнделікті отбасындағы тіршіліктен бастап ғарыштағы күрделі техникалық жүйелерді басқаруға дейін қолданылып отыр. Осы саладағы қол жеткен жетістіктер, бір жағынан, математика ғылымының жедел дамуына байланысты болса, екінші жағынан, электрондық есептеуіш машиналар математиканың дамуына өз әсерін тигізді. Мұның бір дәлелі - ЭЕМ-дер математикалық алгоритмдермен және бағдарламалармен жабдықталғандығында.
Электрондық машиналар арқылы есептеу және ойлау жылдамдығы бірнеше миллион есе артып, ғылым мен техниканың күрделі есептерінің математикалық модельдерін жасауға мүмкіндік туды.
Оптимизация әдістері
§1. Негізгі ұғымдар
1. Анықтамалар. Оптимизация сөзінің астында барлық мүмкіндердің ең жақсы түрін таңдау процесінің мағынасы жатыр. Инженерлік есеп-қисаптар тұрғысынан қарағанда оптимизация әдістері контрукцияның ең жақсы нұсқасын таңдауға, қорларды жақсырақ таратуға мүмкіндік береді.
Оптимизация есептерін шешу барысында берілген есепті анықтайтын кейбір параметрлердің үйлесімді мәндерін табу қажет. Инженерлік есептерді шешу кезінде оларды
жоба параметрлері
деп атау қабылданған, ал экономикалық есептерде оларды
жоспар параметрлері
деп атайды. Жоба параметрлері ретінде, сонымен қатар, объектінің, массаның, температураның және тағы басқалардың сызықтық өлшемдерінің мәндері бола алады.
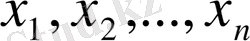 жоба параметрлерінің
n
саны оптимизация есептерінің мөлшерлілігін (және қиындық дәрежесін) сипаттайды.
жоба параметрлерінің
n
саны оптимизация есептерінің мөлшерлілігін (және қиындық дәрежесін) сипаттайды.
Үйлесімді шешімді таңдау немесе екі баламалық шешімдерді салыстыру жоба параметрлерімен анықталатын кейбір тәуелді шаманың (функцияның) көмегімен өткізіледі. Бұл шама мақсаттық функция (немесе сапа критерийі ) деп аталады. Оптимизация есептерін шешу барысында мақсаттық функция минимумді (немесе максимумді) болатын жоба параметрлерінің мәндері табылу керек. Сонымен, мақсаттық функция - бұл инженерлік немесе экономикалық есептер бейнеленетін математикалық модельдердегі үйлесімділіктің глобальды белгісі.
Мақсаттық функцияны мынадай түрде жазып қоюға болады
 (1. 1)
(1. 1)
Инженерлік және экономикалық есеп-қисаптарда кездесетін мақсаттық функцияның мысалы ретінде контрукцияның беріктігі немесе массасы, құрылымның қуаты, өнім шығарудың көлемі, жүктерді тасудың құны, пайда және т . б. бола алады.
Жоба параметрі біреу (n=1) болған жағдайда (1. 1) мақсаттық функциясы бір айнымалының функциясы болып келеді және оның графигі - жазықтықтағы қайсыбір қисық болады. n=2 болған кезде мақсаттық функция екі айнымалының функциясы болады және оның графигі бет болып келеді.
Ескеретін жайт, мақсаттық функция әрқашан формулалар түрінде көрсетілмейді. Кейде ол тек кейбір дискреттік мәндерді ғана қабылдауы, кесте түрінде берілуі және т. б. мүмкін. Барлық жағдайларда ол жоба параметрлерінің бір мәнді функциясы болу тиіс.
Мақсаттық функциялар бірнеше болуы мүмкін. Мысалы, машина жасау бұйымдарын жобалау кезінде бір мезгілде жоғары сенімділік, ең аз материал сыйымдылық, барынша көп пайдалы көлем (немесе жүк көтерімділігі) қамтамасыз ету талап етіледі. Кейбір мақсаттық функциялар сәйкес емес болуы мүмкін. Осындай жағдайларда сол немесе басқа мақсаттық функцияның приоритетін енгізу қажет.
2. Есептерді құру мысалы. Көлемі V=1 м 3 тең тік бұрышты параллелепипед формасындағы контейнерді жобалау керек болсын, сонымен бірге оны дайындауғаазырақ мөлшерде материал жұмсау керек болсын.
Қабырғаларының қалыңдығы тұрақты болған кезде соңғы шарт контейнердің толық бетінің ауданы
S
ең аз болуы керек екенін көрсетеді. Егер контейнер қабырғаларының ұзындығын
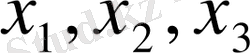 деп белгілесек, онда
деп белгілесек, онда
 (1. 2) функциясын минимизациялау керек болады.
(1. 2) функциясын минимизациялау керек болады.
Осы функция бұл жағдайда мақсаттық болады, ал V=1 - шектеу-теңдеуі шарты бір параметрді табуға мүмкіндік береді:
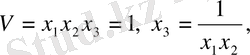
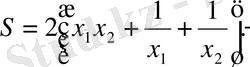 (1. 3)
(1. 3)
Мақсат екі айнымалы функциясының минимализазиялануына әкелінген. Есепті шешу қорытындысында
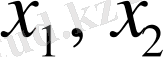 жоба параметрлері, сонан соң
жоба параметрлері, сонан соң
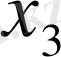 табылады. Шектеу-теңдеуі
табылады. Шектеу-теңдеуі
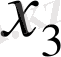 параметрін табу үшін қолданылғандықтан, келтірілген мысалда шынында (1. 3) мақсаттық функциясы үшін шексіз оптимизацияның есебі шықты.
параметрін табу үшін қолданылғандықтан, келтірілген мысалда шынында (1. 3) мақсаттық функциясы үшін шексіз оптимизацияның есебі шықты.
Сонымен бірге, қарастырылып отырған есепті күрделендіруге және қосымша шарттар қоюға болады. Мысалы, берілген контейнердің ұзындығы 2 м-ден кем емес болсын деп талап қояйық. Бұл шарт параметрлердің біреуіне шектеу-теңсіздік түрінде жазылады, мысалы
 (1. 4)
(1. 4)
Осылайша, біз оптимизацияның келесі шартты есебін алдық: (1. 3) -функцияны минималдап және (1. 4) -шектеу-теңсіздігін ескере отырып,
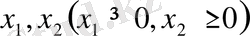 жоспар параметрлерінің мәндерін тауып.
жоспар параметрлерінің мәндерін тауып.
§2. Оптимизацияның көп өлшемді есептері
1. Бірнеше айнымалы функцияларының минимумы. Көбінесе практикалық қызығушылық тудыратын оптимизацияның нақты есептерінде мақсаттық функция көптеген жоба параметрлеріне тәуелді болады.
Көптеген
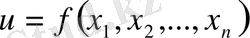 айнымалыларының дифференциалданатын функциясы минимумін оның дифференциал теңдеулер жүйесін шешуден анықталатын критикалық нүктелердің мәндерін зерттей отырып табуға болады
айнымалыларының дифференциалданатын функциясы минимумін оның дифференциал теңдеулер жүйесін шешуден анықталатын критикалық нүктелердің мәндерін зерттей отырып табуға болады
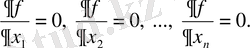 (2. 1)
(2. 1)
М ы с а л. Жоғарыда көлемі 1 м 3 контейнердің оптимал өлшемдерін табу туралы есеп қарастырылды. Есеп оның толық бетін минимализациялауға келтірілді, ол бұл жағдайда мақсаттық функция болып келеді
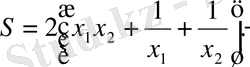 (2. 2)
(2. 2)
Ш е ш і м і. (2. 1) -теңдеуге сәйкес мына жүйені аламыз
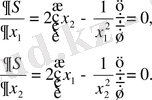
Осы арадан табамыз
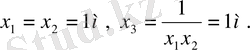 Осылайша, бұл жағдайда контейнердің оптимал формасы қабырғасының ұзындығы 1 м болатын текше болады.
Осылайша, бұл жағдайда контейнердің оптимал формасы қабырғасының ұзындығы 1 м болатын текше болады.
Қарастырылған әдісті тек дифференциалданатын мақсаттық функция үшін қолдануға болады. Бірақ бұл жағдайда да (2. 1) сызықты емес теңдеулер жүйесін шешу кезінде айтарлықтай қиындықтар тууы мүмкін.
Көптеген жағдайларда мақсаттық функция үшін ешқандай формула жоқ болады, тек қарастырылатын облыстың нүктелеріндегі мәндерін кейбір есептеу алгоритмі немесе физикалық өлшеулердің көмегімен табу мүмкіндігі туады. Функцияның барлық облыстағы жеке нүктелердегі белгілі мәндері кезіндегі ең аз мәнін жуықтап анықтау мақсат болады.
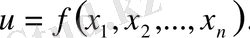 мақсаттық фнукциясының минимумы ізделетін G жобалау облысында осыған ұқсас есепті шешу үшін
мақсаттық фнукциясының минимумы ізделетін G жобалау облысында осыған ұқсас есепті шешу үшін
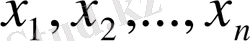 , параметрлерінің интервалдарын
, параметрлерінің интервалдарын
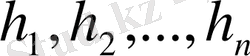 қадамымен бөліктерге бөлшектеу жолымен нүктелердің (түйіндердің) дискреттік жиынын енгізуге болады. Алынған түйіндерде мақсаттық функцияның мәндерін есептеуге болады және бұл мәндердің арасынан ең кішісін табуға болады.
қадамымен бөліктерге бөлшектеу жолымен нүктелердің (түйіндердің) дискреттік жиынын енгізуге болады. Алынған түйіндерде мақсаттық функцияның мәндерін есептеуге болады және бұл мәндердің арасынан ең кішісін табуға болады.
Ескеретін жайт, мұндай әдіс бір айнымалы функция үшін қолданыла алады. Жоба параметрлерінің саны бес және одан көпке жететін оптимизацияның көп өлшемді есептерінде бұл әдіс өте үлкен көлемді есептеулерді талап ететін еді.
Мысалы, бес белгісізі бар функцияның оптимизация есебін шешу кезінде жалпы іздеудің көмегімен есептеу көлемін бағалаймыз. Айталық, оның мәнін бір нүктеде есептеу 100 арифметикалық операцияны талап етсін (тәжірибеде бұл сан бірнеше мыңдарға және одан көпке жетуі мүмкін) . Жобалау облысын әрбір бес бағыттарда 100 бөлімдерге бөлеміз, яғни есептеу нүктелерінің саны 101 5 -не тең, яғни шамамен 10 10 . Сонда арифметикалық операциялардың саны 10 12 -не тең және осы есепті ЭЕМ-де 1 млн. оп. /с жылдамдықпен есептеу үшін 10 6 с (10 тәуліктен көбірек) машиналы уақыт қажет болады.
Жүргізілген бағалау жаппай алмастыруды қолдану арқылы жалпылай іздеу әдісі оптимизацияның көп өлшемді есептерін шешуге жарамайтынын көрсетеді. Мақсатқа бағытталған іздеуге негізделген арнайы сандық әдістер қажет. Солардың кейбіреуін қарастырамыз.
2. Координатты түсіру әдісі.
Айталық,
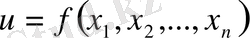 мақсаттық функциясының ең аз мәнін табу талап етілсін. Бастапқы жуықтау ретінде
n
өлшемді кеңістігінде кейбір
мақсаттық функциясының ең аз мәнін табу талап етілсін. Бастапқы жуықтау ретінде
n
өлшемді кеңістігінде кейбір
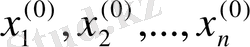 координаталы
М
0
нүктесін таңдаймыз.
u
функциясының біріншіден басқа барлық координаталарын жазып қоямыз. Сонда,
координаталы
М
0
нүктесін таңдаймыз.
u
функциясының біріншіден басқа барлық координаталарын жазып қоямыз. Сонда,
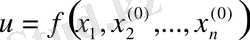 - бір
- бір
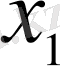 айнымалы функциясы. Оптимизацияның бір өлшемді есебін шеше отырып, біз
u
функциясы қалған координаталарда жазып алынған кездегі
x
1
координатасы бойынша ең аз мән қабылдайтын
М
0
нүктесінен
айнымалы функциясы. Оптимизацияның бір өлшемді есебін шеше отырып, біз
u
функциясы қалған координаталарда жазып алынған кездегі
x
1
координатасы бойынша ең аз мән қабылдайтын
М
0
нүктесінен
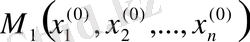 нүктесіне өтеміз. Мұнда
нүктесіне өтеміз. Мұнда
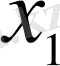 координатасы бойынша түсіруде жататыноптимизация процесінің алғашқы қадамы жатыр.
координатасы бойынша түсіруде жататыноптимизация процесінің алғашқы қадамы жатыр.
Енді
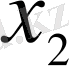 басқа барлық координаталарды жазып аламыз және осы айнымалының
басқа барлық координаталарды жазып аламыз және осы айнымалының
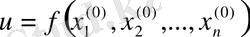 функциясын қарастырамыз. Қайтадан оптимизацияның бір өлшемді есебін шеше отырып, оның
функциясын қарастырамыз. Қайтадан оптимизацияның бір өлшемді есебін шеше отырып, оның
 кездегі ең аз мәнін табамыз, яғни
кездегі ең аз мәнін табамыз, яғни
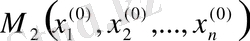 нүктесіндегі. Осыған ұқсас
нүктесіндегі. Осыған ұқсас
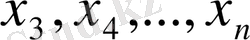 координаталары бойынша түсіру жүргізіледі, ал содан соң процедура қайтадан
координаталары бойынша түсіру жүргізіледі, ал содан соң процедура қайтадан
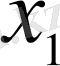 -ден
-ден
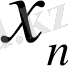 -ге дейін қайталанады және т. б. Осы процесс қортындысында мақсаттық функцияның мәні
-ге дейін қайталанады және т. б. Осы процесс қортындысында мақсаттық функцияның мәні
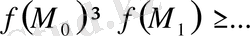 монотонды кемімелі тізбек құрайтын
монотонды кемімелі тізбек құрайтын
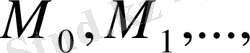 нүктелер тізбегі алынады. Кез келген
k
-ші қадамда бұл процесті үзуге болады және
f(M
k
)
мәні қарастырылып отырған облыстағы мақсаттық функцияның ең кіші мәні ретінде қабылданады.
нүктелер тізбегі алынады. Кез келген
k
-ші қадамда бұл процесті үзуге болады және
f(M
k
)
мәні қарастырылып отырған облыстағы мақсаттық функцияның ең кіші мәні ретінде қабылданады.
Осылайша, координатты түсіру әдісі көп айнымалы функциялардың ең кіші мәнін табу туралы есепті оптимизацияның бір өлшемді есептерін әрбір жоба параметрі бойынша қайта-қайта шешілуіне алып келеді.
Берілген әдісті үш өлшемді кеңістікте кейбір бетті суреттейтін екі айнымалының
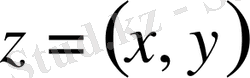 функциясының жағдайы үшін геометриялық түрде көркемдеу оңай.
функциясының жағдайы үшін геометриялық түрде көркемдеу оңай.
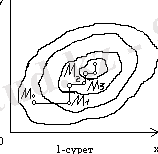
1-суретте осы беттің деңгей сызықтары жүргізілген. Бұл жағдайда оптимизация процесі келесі бейнемен жүреді.
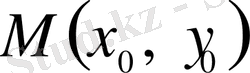 нүктесі бастапқы жуықтауды бейнелейді.
x
координатасы бойынша түсіру жүргізе отырып,
нүктесі бастапқы жуықтауды бейнелейді.
x
координатасы бойынша түсіру жүргізе отырып,
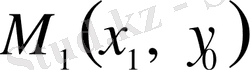 нүктесіне түсеміз. Онан әрі, ординаталар осьіне паралель қозғала отырып,
нүктесіне түсеміз. Онан әрі, ординаталар осьіне паралель қозғала отырып,
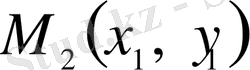 нүктесіне келеміз және т. б.
нүктесіне келеміз және т. б.
Бұл жерде оптимизацияның қарастырылып отырған процесінің жинақтылығы туралы сұрақ маңызды болып табылады. Басқаша айтқанда, мақсаттық функция мәнінің
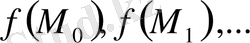 тізбегі берілген облыстағы оның ең кіші мәніне келе ме? Бұл - функция түріне және бастапқы жуықтауды таңдауға тәуелді болады.
тізбегі берілген облыстағы оның ең кіші мәніне келе ме? Бұл - функция түріне және бастапқы жуықтауды таңдауға тәуелді болады.
2-сурет. Координатты түсіру әдісінің блок-схемасы
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz