Транспорт есебінің моделі

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 16 бет
Таңдаулыға:

Қазақстан Республикасының білім және ғылым министрлігі

БҚОББ «Орал газ, мұнай және салалық технологиялар колледжі» МКҚК

«Математика және информатика»

ПЦК-сы

Курстық жұмыс

Пәні: «Өндірістік және экономикалық процестерді модельдеу»

Тақырыбы: «Транспорттық есеп»

Орындаған: СТ- 441 топ оқушысы

Нуртазина Н. Н

Тексерген: жетекші Лукпанова Д. М

Орал 2007

Мазмұны

І. Кіріспе . . . 3

ІІ. Негізгі бөлім

2. 1. Транспорт есебінің моделі . . . 5

2. 2. Алғашқы таяныш жоспарларды анықтау . . . 7

2. 3. Транспорт есебінің оптимал шешімі.

Потенциалдар әдісі . . . 9

2. 4. Excel программасының көмегімен транспорттық

есептің шешімін табу . . . 16

ІІІ. Қорытынды . . . 20

ІV. Қолданылған әдебиеттер . . . 21

Кіріспе

Қазіргі қоғамда болып жатқан ақпараттық дамудың өңделу, жеткізілу, сақталу заңдарының негізін ұғыну және дұрыс болжамдау үшін болашақ маманға компьютерлік модельдеу, ақпаратты өңдеу аса қажет.

Модельдеу - қазіргі заманғы ғылыми танымның басқарушы принципі. Адам таным затын оның барлық процестерінде толық көре алмайды. Сондықтан ол объектінің өзінің алдында тұрған мәселені шешуге қажетті жағын тануға ұмтылады.

Компьютерлік математикалық модельдеу информатика пәнімен технологиялық жағынан байланысады.

Сондай-ақ, ЭММ пәнін оқып үйрену кезінде математикалық программалау тақырыбының алатын орны ерекше.

Математикалық программалау шектеулі ресурстарды барынша тиімді пайдаланып, қойылған мақсатқа қол жеткізуді үйрететін математиканың саласы.

Әдетте математикалық программалау есебі екі бөліктен атап айтсақ, мақсатты функциядан f(х _1, х ₂ , х ₃ , . . . , х _n ) және есеп шарттарынан g _i ([х _1, х ₂ , х ₃ , . . . , х _n ] ) ≤b _i тұрады. Мұнда i=1 . . . m, ал j=1 . . . n дейін өзгереді, ал b _i - i-ші өндіріс ресурстарынның көлемін сипаттайтын шама.

Математикалық программалаудың 2 түрі бар: сызықтық программалау және сызықтық емес программалау.

Математикалық программалаудың қазіргі кезде көбінесе сызықтық теңсіздіктер немесе теңдеулер түрінде шарт қойылған, сызықтық функцияның ең үлкен немесе ең кіші мәнін табу.

Сызықтық программалаудың транспорт есептері экономикалық процестерді зерттеулер мен теориялық ізденістерде кеңінен қолданылады. Әсіресе өнеркәсіп және ауылшаруашылық өнімдерін тасымалдаудың ұтымды жоспарларын анықтап, әр түрі транспорттың тиімді жұмыс істеуін қамтамасыз етеді.

2. 1. Транспорт есебінің моделі

Транспорт есебінің математикалық қойылуы:

m жабдықтаушыда біркелкі өнім (жүк) жинақталған және оның әр жабдықтаушыдағы мөлшері а _і - ге (і=1, m) тең делік. Осы өнімдерді n - тұтынушылардың әрқайсысына b _j - ге (j=1, n) мөлшерінде жеткізу керек. Әр жабдықтаушыдан тұтынушыларға жүктің жеке бір бөлігін тасымалдау шығыны с _ij - ге тең. Олай болса, әр тұтынушының қажетін толық қанағаттандыратын әрі толық транспорт шығыны ең аз болатын жүк тасымалдаудың жоспарын табу қажет.

Егер x _ij деп і жабдықтаушысынан j - тұтынушысына тасымалданатын жүктің мөлшерін белгілесек, онда есептің берілгенін төмендегі кесте түрінде бейнелеуге болады.

Жабдықтау-шылар

Тұтынушылар

Жабдықтау- шылар

В ₁

В ₂

. . .

В _n

Жабдықтау-шылар: А ₁

Тұтынушылар:

С ₁₁

Х ₁₁

Жабдықтау- шылар:

С ₁₂

Х ₁₂

…

C _1n

X _1n

a ₁

Жабдықтау-шылар: А ₂

Тұтынушылар:

С ₂₁

Х ₂₁

Жабдықтау- шылар:

C ₂₂

X ₂₂

…

C _2n

X _2n

a ₂

Жабдықтау-шылар: . . .

Тұтынушылар: . . .

Жабдықтау- шылар: …

…

Жабдықтау-шылар: А _m

Тұтынушылар:

С _m1

X _m1

Жабдықтау- шылар:

C _m2

X _m2

…

С _mn

Х _mn

a _m

Жабдықтау-шылар:

Тұтынушылар: b ₁

Жабдықтау- шылар: b ₂

…

b _m

Бұл кестеде есептің негізгі үлестіру кестесі деп аталады. Егер есептің берілуі бойынша барлық жабдықтаулардағы жүк қорларының қосындысы мен тұтынушылардың қажеттіліктерінің қосындысы тең немесе мына

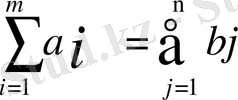
шарт орындалатын болса, онда бұндай есепті транспорт есебінің жабық моделі деп, ал орындалмаса ашық моделі деп атайды.

Транспорт есебінің моделінің жалпы түрі төмендегідей жазылады:

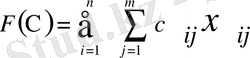
мақсат функциясына минимал мән әперетін және мына:

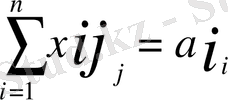i =1, 2, . . . , m

, j = 1, 2, . . . , n

x _ij = 0, i = 1, 2, …, m; j = 1, 2, …, n

шарттарын қанағаттаныратын Х = (Х _ij ) _mxn жүк тасымалдау жоспарын табу қажет.

Мысалы. Кестеде берілген транспорт есебінің моделін құру

а _i b _j

аibj: 60

20: 5

30: 6

40: 3

аibj: 50

20: 2

30: 4

40: 8

Шешуі: і - ші жабдықтаушыдан j - ші тұтынушыға жеткізілетін жүк мөлшерін х _ij ≥0 (i=1, 2) ; (j=1, 2, 3) деп белгілеп, алты айнымалы енгізіп, келесі математикалық модельді аламыз:

тұтыну мөлшері бойынша,

х _ij ≥ 0 (i=1, 2, 3)

теріс еместік шарты.

Мақсат функциясы:

Ғ(х) = 5х ₁₁ + 6х ₁₂ + 3х ₁₃ + 2х ₂₁ + 4х ₂₂ + 8х ₂₃ → min

Ескерту: Жабдықтаушылар қоры бойынша шектеулер теңсіздіктер түрінде берілген, себебі ∑а _і = 110 >∑b _j = 90, сондықтан жүктің артық 20 бірлігі жабдықтаушыларда қалады.

2. 2. Алғашқы таяныш жоспарларды анықтау

Транспорт есебінің алғашқы таяныш жоспарын табудың бірнеше қарапайым әдістері бар. Солардың арасында жиі қолданатыны «солтүстік-батыс бұрышы» әдісі мен «минимал элемент» әдісі. Транспорт есебінің жалпы теңдеулер жүйесі өзара сызықтық тәуелді болады да, ал сызықтық тәуелсіз теңдеулерінің саны m + n -1 -ге тең болады. Сондықтан транспорт есебінің айнымаған алғашқы таяныш жоспарында m + n -1 оң құрамы боп, қалған компоненттері 0-ге тең болады.

Келесі транспорт есебінің алғашқы таяныш шешімін «солтүстік-батыс бұрышы» және «минимал элемент» әдістерімен тауып, ол шешімдердің сызықтық функционалының мәндерін салыстырамыз.

а _i b _j

70 b _j

аibj: 100

90:

40:

50: 4

70 bj: 5

аibj: 70

90: 5

40:

50:

70 bj: 6

аibj: 80

90: 1

40: 6

50:

70 bj:

Шешуі: 1. «Солтүстік - батыс бұрышы» әдісінде кестені толтыру сол жақтағы ең жоғарғы клеткадан басталады. (Географиялық картадағы солтүстік - батысқа сәйкес) . Х ₁₁ - дің мәнін мына қатынастан табамыз: х ₁₁ =min {a _1, b ₁ }. Егер а ₁ < b ₁ болса, онда х ₁₁₌ а ₁ , ал а ₁ > b ₁ болса, х ₁₁ = b ₁ тең, қалған жүкті ары қарай үлестіре отырып, ең соңғы клетка толтырылған соң алғашқы таяныш жоспарын аламыз. Алынған таяныш айнымаған, себебі толтырылған клеткалар саны m + n - 1 = 3 + 4 - 1 = 6 - ға тең.

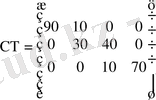
Осы таяныш жоспарға сәйкес сызықтық функционалдың мәнін немесе жалпы шығынын есептейік:

Ғ(x ^' T) = 90*7 + 10*3 + 30*7 + 40*3 + 10*5 + 70*3 = 630 + 30 + 210 + 50 + 210 = 1250

Шешуі: 2. «Минимал элемент» әдісінде транспорт тарифы ескеріледі. Кестені толтыру ең кіші элементтен басталады. Минимал элемент әдісін пайдаланып х _ij - дің мәнін табу үшін, транспорт тарифін көрсететін с _ij матрицасынан ең кіші элемент табылып, сол клеткаға а _і мен b _j - дің кішісі жазылады. Содан соң, бұдан кейінгі зерттеуден і - ші қатар (егер х _ij = a _i , болса) немесе j - баған (егер x _ij = b _j болса) шығарылады және тұтынушының

Қажеті немесе жабдықтаушыдағы жүктің қоры x _ij = a _i = b _j болса, онда бұдан кейінгі зерттеуден і - ші қатар мен j - ші баған шығарылады. Содан соң, матрицаның қалған эелементтерінен де минимал элемент анықталып, жоғарыда келтірілген амалдар қайталанады. Бұл процесс барлық жүктің қоры үлестіріліп және тұтынушылардың қажеті толық қанағаттандырылғанға дейін жалғанады. Алдыңғы қарастырған кестені осы әдіспен толтырайық.

а _i b _j

70 b _j

аibj: 100

90: 7

40:

50: 4

70 bj:

аibj: 70

90:

40: 7

50:

70 bj:

аibj: 80

90:

40: 6

50: 5

70 bj: 3

Нәтижесінде айнымаған келесі жоспарды аламыз:

Сәйкес сызықтық функционалының мәні:

Ғ(х ^'' т) = 40*3 + 60*5 + 10*5 + 50*3 + 10*6 + 80*1 = 760

Сызықтық функционалдың екі әдіс бойынша табылған мәндерін салыстырып, соңғы әдіс бойынша табылған таяныш жоспарға транспорт шығыны аз жұмсалғанын көреміз.

Ғ(х ^' _т ) =125, Ғ(х ^'' _т ) =760.

Әрине, бұдан барлық уақытта «минимал элемент» әдісі бойынша жақсы жоспар табылады деп жорамалдауға болмайды.

2. 3. Транспорт есебінің оптимал шешімі.

Потенциалдар әдісі

Алғашқы таяныш жоспар табылғаннан соң потенциалдар әдісінің көмегімен есептің оптимал шешімін табуға болады. Потенциалдар әдісінің негізгі алгоритмін келтірейік:

Жоғарыда келтірілген әдістердің бірімен алғашқы таяныш жоспар алынады.
Табылған жоспардың оптимал екенін тексеру үшін потенциалдар системасы құрылады. ui- қатар, vj- баған потенциалдары деп есептесек, онда әрбір жабық клетка үшін ui+ vj= cijтеңдеуі құрылады. Нәтижесінде m+n белгісіздері бар m+n-1 теңдеулер жүйесін аламыз. Бұл жүйенің белгісіздерінің саны теңдеулерінің санынан көп болғандықтан, оның көп шешімі болады. Сондықтан осы системаның кез келген бір шешімін алу үшін ui-дің біреуін нөлге тең деп алып, қалған потенциалдарды анықтаймыз. Мысалы: ui-дің мәні белгілі десек, онда ui+ vj= cijтеңдеуінен vj= cij- uiтабылады.
Әрбір бос клетка үшін ui+ vj>cijшарты орындалуын тексереміз. Егер осы шарт барлық бос клетка үшін орындалса, онда алынған жоспар оптимал болғаны.
Егер кемінде бір бос клетка үшін ∆ij=(ui+ vj) - cij>0 болса, онда жоспар жаңа жоспармен алмастырылады. Ол үшін ∆ij>0 клеткалар арасынанклеткасы таңдалып алынып, оған үлестіретін λ - жүк мөлшері жазылады.
λ -санын табу үшін жоғарыда анықталған (1, k) клеткасына (+) таңбасын жазып, сол клеткадан бастап төбелері жабық клеткаларда жататындай етіп, тік бұрышты тұйық контур саламыз. Осы контурдың қалған төбелеріне (+) және (-) таңбаларын алмастыра отырып, жазып шығамыз.
Үлестіруге тиісті жүк мөлшерін (-) таңбасы бар клеткаларда орналасқан хij-дің ең кішісіне тең деп аламыз.

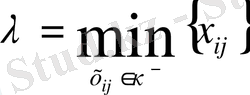
k ^- - контурдың (-) пен белгіленген белгілеген төбелері. Содан соң λ - санын (-) таңбасы бар клеткалардағы жүк мөлшерінен алып тастаймыз, ал (+) таңбасы бар клеткадағы жүк мөлшеріне қосып жазып жаңа жоспар аламыз.

Табылған жаңа жоспар қайтадан тексеріледі. Ол үшін 2-6 қадамдарды орындаймыз.

2-есеп. Бірінші есептегі «Солтүстік-батыс бұрышы» әдісімен алынған таяныш жоспарды потенциалдар әдісімен оптимал мәніне тексерейік.

а _і b _j

u _i

аіbj: 100

90:

40:

10 +

50: 4

70: 5

ui: u ₁ = 0

аіbj: 70

90: 5

40:

30 -

50:

40 +

70: 6

ui: u ₂ = 4

аіbj: u _i

90:

40: 8

50:

10 -

70:

ui: u ₃ = 6

аіbj: v _j

90: v ₁ = 7

40: v ₂ = 3

50: v ₃ = -1

70: v ₄ = -3

ui:

Шешуі: Алынған таяныш жоспар айнымаған. u ₁ = 0 деп алып, қалған потенциалдарды анықтаймыз.

u ₁ + v ₁ = 7 v ₁ = 7

u ₁ + v ₂ = 3 v ₂ = 3

u ₂ + v ₂ = 7 u ₂ = 4

u ₂ + v ₃ = 3 v ₃ = -1

u ₃ + v ₃ = 5 u ₃ = 6

u ₃ + v ₄ = 3 v ₄ = -3

Потенциалдар жүйесі құрылды:

U = (0; 4; 6) ; V = (7; 3; -1; -3)

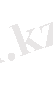
Барлық бос клеткалар үшін ∆ _ij = (u _i + v _j ) - c _ij мәндерін анықтаймыз.

∆13= u1+ v3- c13= 0-1-4=-5 <0
∆14= u1+ v4- c14= 0-3-5=-8 <0
∆21= u2+ v1- c21= 4+7-5=6>0
∆24= u2+ v4- c24= 4-3-6=-5 <0
∆31= u3+ v1- c31= 6+7-1=12 >0
∆32= u3+ v1- c32= 6+3-6=3 >0

Анықталған барлық ∆ _{ij -} дің мәндерін қарастыра келіп, А ₂ В ₁ , А ₃ В ₁ , А ₃ В ₂ клеткаларындағы мәндердің оң екенін көреміз. Демек, табылған жоспар оптимал емес. Осы клеткалардың ең үлкен мәні А ₃ В ₁ - ге сәйкес келеді. Сондықтан, оны жабық клеткаға айналдыру керек. Ол үшін осы клеткадан бастап төбелері жабық клеткада жататындай етіп тік бұрышты контур тұрғызамыз. Контурдың А ₃ В ₁ клеткасына (+) таңбасын, ал қалған төбелеріне (+) пен (-) таңбаларын алмастырып жазамыз.

Үлестірілуі тиіс жүк мөлшері λ - ны мына шарттан анықтаймыз. Берілген есепте λ = min{90, 30, 10}=10.

Жаңа жоспарды анықтау үшін контурдың (+) таңбалы төбелеріне

λ = 10 - ды қосып, ал (-) таңбалы төбелерінен алып тастаймыз. Кестенің қалған мәндері еш өзгеріссіз келесі кестеге көшеді. Нәтижесінде төмендегі кестеде жаңа жоспарды аламыз:

а _і b _j

u _i

аіbj: 100

90:

40:

20 +

50: 4

70: 5

ui: u ₁ = 0

аіbj: 70

90: 5

40:

20 -

50:

50 +

70: 6

ui: u ₂ = 4

аіbj: 80

90:

40: 8

50: 5

70:

ui: u ₃ = -6

аіbj: v _j

90: v ₁ = 7

40: v ₂ = 3

50: v ₃ = -1

70: v ₄ = 9

ui:

Алынған жоспар айнымаған, себебі жабық клеткалар саны m + n - 1 = 4+3-1=6 - ға тең. Осы жоспар бойынша транспорт шығынын есептейік:

Ғ=80*7+20*3+20*7+50*3+10*1+70*3=560+60+140+150+10+210=1130

Жаңа жоспарды оптималдыққа тексеру үшін потенциалдарды анықтаймыз.

u ₁ =0

u ₁ + v ₁ = 7 v ₁ = 7

u ₁ + v ₂ = 3 v ₂ = 3

u ₃ + v ₁ = 1 u ₂ = -6

u ₂ + v ₂ = 7 v ₃ = 4

u ₂ + v ₃ = 3 u ₃ = 6

u ₃ + v ₄ = 3 v ₄ = 9

Бос клеткалар үшін ∆ _{ij -} дің мәндерін анықтаймыз:

∆ ₁₃ =-5 <0, ∆ ₁₄ =4>0, ∆ ₂₁ =6>0,

∆ ₂₄ =7 <0, ∆ ₃₂ =-9 <0, ∆ ₃₃ =-12 <0

А ₁ В ₄ , А ₂ В ₁ , А ₂ В ₄ клеткаларында оптималдық шарты орындалмайды. А ₂ В ₁ клеткасынан бастап контур сызамыз. λ мөлшерін анықтаймыз:

λ= min{80, 20}=20.

Келесі кестеде жаңа жоспар аламыз:

а _і b _j

u _i

аіbj: 100

90:

40:

50: 4

70: + 5

ui: u ₁ = 0

аіbj: 70

90:

40: 7

50:

70: 6

ui: u ₂ = -2

аіbj: 80

90:

10 +

40: 8

50: 5

70:

70 -

ui: u ₃ = -6

аіbj: v _j

90: v ₁ = 7

40: v ₂ = 3

50: v ₃ = 5

70: v ₄ = 9

ui:

Айнымаған жоспар алынды. Транспорт шығынын есептейік:

Ғ=60*7+40*3+20*5+50*3+10*1+70*3=1010

Алынған жоспарды оптималдыққа тексереміз, потенциалдарды анықтайыз: u ₁ =0

u ₁ + v ₁ = 7 v ₁ = 7

u ₁ + v ₂ = 3 v ₂ = 3

u ₂ + v ₁ = 5 u ₂ = -2

u ₂ + v ₃ = 3 v ₃ = 5

u ₃ + v ₁ = 1 u ₃ =-6

u ₃ + v ₄ = 3 v ₄ = 9

Бос клеткалар үшін ∆ _ij - дің мәндерін қарастыра келіп, А ₁ В ₄ , А ₂ В ₄ , А ₃ В ₂ клеткаларындағы мәндердің оң екендігін көреміз. Жоспар оптимал емес. А ₁ В ₄ клеткасы бойынша тік бұрышты тұйық контур тұрғызамыз. λ мөлшерін анықтаймыз:

λ= min{60, 70}=60

Келесі кестеде жаңа жоспар аламыз:

а _і b _j

u _i

аіbj: 100

90: 7

40:

50: 4

70:

ui: u ₁ = 0

аіbj: 70

90:

40: 7

50:

70: + 6

ui: u ₂ = 2

аіbj: 80

90:

70 +

40: 8

50: 5

70:

10 -

ui: u ₃ = -2

аіbj: v _j

90: v ₁ = 3

40: v ₂ = 3

50: v ₃ = 1

70: v ₄ = 5

ui:

Айнымаған жоспар алынды. Транспорт шығынын есептейік:

Ғ=40*3+60*5+20*5+50*3+70*1+10*3=770

Алынған жоспардың оптималдыққа тексереміз, потенциалдарды анықтаймыз:

u ₁ =0

u ₁ + v ₂ = 3 v ₂ = 3

u ₁ + v ₄ = 5 v ₄ = 5

u ₃ + v ₄ = 3 u ₃ = -2

u ₃ + v ₁ = 1 v ₁ = 3

u ₂ + v ₁ = 5 v ₂ = 2

u ₂ + v ₃ = 3 v ₃ = 1

Бос клеткалардың үшін ∆ _ij - дің мәндерін анықтаймыз:

∆ ₁₁ =-4 <0, ∆ ₁₃ =-3<0, ∆ ₂₂ =-2<0,

∆ ₂₄ =1 <0, ∆ ₃₂ =-5 <0, ∆ ₃₃ =-6 <0

Осы анықталған мәндер бойынша бір клеткада, яғни А ₂ В ₄ оптималдық шарты орындалмайды. Сондықтан, осы клеткадан тұйық тік бұрышты контур тұрғызып, λ мөлшерін анықтап, λ= min{20, 100}=10, жаңа жоспар аламыз:

а _і b _j

u _i

аіbj: 100

90: 7

40:

50: 4

70:

ui: u ₁ = 0

аіbj: 70

90:

40: 7

50:

70:

ui: u ₂ = 1

аіbj: 80

90:

40: 8

50: 5

70: 3

ui: u ₃ = -3

аіbj: v _j

90: v ₁ = 4

40: v ₂ = 3

50: v ₃ = 2

70: v ₄ = 9

ui:

Айнымаған жоспар алынды. Транспорт шығынын есептейік:

Ғ=40*3+60*5+10*5+50*3+10*6+80*1=760

Алынған жоспардың оптималдыққа тексереміз, потенциалдарды анықтаймыз:

u ₁ =0

u ₁ + v ₂ = 3 v ₂ = 3

u ₁ + v ₄ = 5 v ₄ = 5

u ₃ + v ₄ = 6 u ₃ = 1

u ₃ + v ₁ = 5 v ₁ = 4

u ₂ + v ₃ = 3 v ₃ = 2

u ₃ + v ₁ = 1 v ₃ = -3

Бос клеткалардың үшін ∆ _ij - дің мәндерін анықтаймыз:

∆ ₁₁ =-34 <0, ∆ ₁₃ =-2<0, ∆ ₂₂ =-3<0,

∆ ₃₂ =-3 <0, ∆ ₃₃ =-6 <0, ∆ ₃₄ =-1 <0

Демек, барлық бос клеткалар үшін ∆ _ij <0 болғандықтан, соңғы табылған жоспар оптимал болады. Сонымен

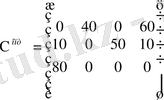; Ғ(Х ^опт ) =760

2. 4. Excel программасының көмегімен транспорттық

есептің шешімін табу

«Солтүстік-батыс бұрышы» мен «минимал элемент» әдістерімен шығарылған есепті Excel жүйесінде қарастырайық.

Жабдықтаушылардың қуаттылығы

Тұтынушылардың қуаттылығы

Жабдықтаушылардың қуаттылығы: 100

Тұтынушылардың қуаттылығы: 7

Жабдықтаушылардың қуаттылығы: 70

Тұтынушылардың қуаттылығы: 5

Жабдықтаушылардың қуаттылығы: 80

Тұтынушылардың қуаттылығы: 1

Есептің шешімін табу үшін мынадай қадамдар орындау қажет:

Есептің шешімін табу үшін форма құру.

Бұл қадамда жүк тасымалы матрицасы құрылуы қажет. Ол үшін өзгеретін ұяшықтарды резервтеу қажет, сол себепті В3:В5 ұяшықтарына «1» санын енгізі арқылы сол орынды резервтейміз. Есептің шешімін тапқаннан кейін бұл орындарда жүк тасымалдауға кететін шығындар саны көрсетіледі.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.