АТМОСФЕРАНЫҢ ШЕКАРАЛЫҚ ҚАБАТЫНЫҢ САНДЫҚ ҮЛГІЛЕРІ

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 33 бет
Таңдаулыға:

Жұмыстың өзектілігі:
Жаңа талаптарға сәйкес ғылым және техника үшін лабораториялық және
табиғи жағдайларда экспериментальдық зерттеу өте күрделі және қымбат, кей
жағдайларда тіпті мүмкін емес болғандықтан, қазіргі кезде жылу-масса
алмасу процестерін сандық үлгілеудің маңызы зор. Жылу мен масса алмасу
процестерін сандық үлгілеу әртүрлі ғылыми-зерттеу, конструкторлық-жобалау
және өндірістік мекемелерінің жұмыс тәжірибесіне сәтті кіруде. Мұндай
мекемелердің көпшілігі есептеу мүмкіндігі жоғары компьютерлермен
жабдықталған.
Сандық моделдеу тәсілдері салыстырмалы түрде бұрыннан қолданылады.
Бірақ соңғы уақытта есептеу техникасының қарқынды дамуы, ресурстық
есептеулер жүргізуге және физикалық тұрғыдан ақталған нәтижелер алуға
мүмкіндік берді. Сонымен қатар суперкомпьютерлерді және параллель
бағдарламаларды қолдану есептеу өнімділігін (сонымен бірге дәлдікті)
бірнеше есе жоғарлатады.
Қазіргі уақытта көппроцессорлы жүйеде параллель бағдарламалаудағы, ең
дамыған жүйе болып табылады. Көппроцессорлы жүйе тиімді, сенімді және
тасымалданатын жоғарғы деңгейлі параллель бағдарламаларды құруға мүмкіндік
береді.
Бұл курстық жұмыста шекаралық қабаттың қалыңдығын, жер үстінен 5-10 м
биіктіктен бастап атмосфераның жоғарғы қабатына дейін алынып, яғни жер
бедері мен қаланың биік ғимараттарынан туатын кедергілерді жалған облыстар
әдісін қолдана отырып сипатталынған. Өте күрделі физикалық процестердің
математикалық үлгілерін толық параметрлік зерттеуге жаңа талаптарға сай
есептеу әдістері мен компьютерлер мүмкіндік береді. Осындай зерттеуді
сандық эксперимент деп атайды.

1 АТМОСФЕРАНЫҢ ҚҰРЫЛЫМЫ ЖӘНЕ ОНДАҒЫ АУА ҚОЗҒАЛЫСЫ

Атмосфера (грек. atmos – бу және shaira – шар) – Жер шарының өзімен
бірге айналатын және оның тәуліктік, жылдық айналымына қатысы бар газ
қоспаларынан тұратын ауа қабаты. Ол газдан, су тамшыларынан, шаңнан, мұз
кристалдарынан тұрады. Массасы 5,15*1015 т. Жер бетінен жоғарылаған сайын
Атмосфераның қысымы мен тығыздығы төмендей түседі де, біртіндеп планета
аралық кеңістікке ұласып кетеді.

1.1 Атмосфераның қабаттық құрылымы

Температураның өзгеруіне қарай Атмосфера тропосфера, стратосфера,
мезосфера, термосфера және экзосфера қабаттарына ажырайды. Жер үстіндегі
бірінші қабат – тропосфера қабаты, оның биіктігі 10-12 км, ал экватордың
үстінен есептегенде 16-18 км биіктікте орналасқан. Тропосферада
атмосфераның 80 %-і шоғырланған. Осы қабатта әрбір 1 км жоғары көтерілген
сайын ауа температурасы 60-қа төмендейді. Тропосфераның үстінде қалыңдығы
80 км-ге дейін жететін стратосфера қабаты мен ионосфера қабаты орналасқан.
Тропосфера қабатынан қысқа толқынды радиациялардың өтуіне қатысты оны
жұқа қабат деп айтуға болады. Атмосфераның шашыранды Күн радиациясын
жартылай өзіне сіңіріп, өзінен ұзын толқынды инфрақызыл сәуле бөліп
шығарады, сонымен қатар жер бетінің ұзын толқынды сәулесінің ¾-ін қайта
сіңіреді. Жер беті мен Атмосфера арасында жылу және ылғал тұрақты.
Сондықтан, атмосфераның қабаттарында оның жалпы айналым әрекеттерімен
қатар, физикалық процестер де жүріп жатады. Атмосфераның нақты жоғарғы
шекарасын көрсетуге болмайды, себебі ауаның тығыздығы биіктікпен бірге
азайып отырады. Жер бетінде құрғақ ауаның тығыздығы 0 °С –та орта есеппен
1290г м3, ал 10 км биіктікте 400гм3, 20 км биіктікте жуық шамамен 90 г
м3 тең болады.
Сонымен, тропосфера күннің сәулелеріне қатысты мөлдір болғанмен, ол
біріншіден, ауаның вертикальды ауысуы мен су буының конденсациясы,
бұлттардың түзілуі және жауын-шашынның болуы жер қабатынан бастап
қыздырылады. Трапосферада температура орта есеппен әрбір 100 м биіктікте
0,5-0,6 °С-қа азаяды.
Стратосфера қабатының 15-60 км биіктігінде ультракүлгін сәулелерді
қарқынды сіңіретін аз мөлшерде азон қабаты бар, сондықтан мұнда
температураның кемуі тоқтатылады, ал 30-40 км биіктікте температураның өсуі
байқалады, 60 км биіктікте температура +75 °С жетеді, осыдан кейін 80 км
биіктікте температура -75°С қайтадан азаяды (1-сурет). Стратосферада су
буы мүлдем болмайды, себебі онда жауын-шашын тудыратын бұлттар жоқ.
Атмосферада температураның анықталуы: атмосфераның төменгі
қабаттарына және жер бетінің қасиетіне, сонымен қатар, жердің, судың,
құрғақ даланың біртекті орналасуы географиялық көлемге байланысты.
Температураның бірқалыпсыз орналасуы қысымның бірқалыпсыз
орналасуына әкеліп соғады. Нәтижесінде атмосфераның ортақ церкуляциясы
құрылып, ауа ағындары пайда болады.

Сурет 1.1. Атмосфера қабаттары

Атмосфера қабаты биік болғанмен, ауа райына тек қана тропосфера
қабаты әсер етеді. Тропосфера тұрақты болмайды, себебі онда су буы
конденсациясын тудыратын және бұлттар мен жауын-шашын пайда болатын
вертикальды ағындар түрленеді.
Ауаның вертикаль бағытты бойынша ауысу жылдамдығы горизонталь
бағытпен салыстырғанда көп жағдайда айқындалмайтын өлшемдер құрады. Ауаның
вертикаль бағыты бойынша үлкен кедергілердің үстіндегі орташа жылдамдығы
орта есеппен 7 смс.
Ауа массасының диффузияға қабілеттілігі температураның вертикаль
бойынша орналасуымен анықталады.
Атмосферада әр 100 метр сайын температураның өзгеруін температура
градиенті деп атайды. Барлық биіктіктерде өзгермеген температурада
вертикальды градиент температурасын изометриялық деп атайды.

1.2 Жер бедерінің тегіс емес жерлерін ауа ағындарының орағытып
ағуы

Атмосферадағы ауа массасының қозғалыс бағыты баричтің градиенттік
бағытымен сәйкес келмейді, яғни бірдей аралықтағы қысымның төмендеу
өлшемдерімен қандай да бір бұрышты құрайды. Сонымен ауаның қозғалыс
массасының өзгеруіне Жердің айналу күші мен қажалу күші әсер етеді. Жердің
айналу күшін Кориолис күші деп атайды.
Қажалу күші жер қабатында пайда болады және жер бедерінің тегіс емес
жерлеріне ескеріледі. Қажалу күші сонымен қатар әр түрлі қозғалыстағы ауа
қабаттарының арасында пайда болады. Биіктіктің өсу бойынша шегіндіру
(отклонения) бұрышы да тез өседі және 1000 м биіктікте 50С максимальды
мәнге ие болады. Сонымен, ауа қозғалысы изобара бағытымен, яғни түзудегі I
бірдей атмосфераның қысымы бағытымен қозғалады. Мұндай жел градиент деп
аталады. 500 м биіктікте жел бағыт бойынша шамамен 20-ға шегіндіреді.
Жер үстінің бірқалыпты қызбауы және жер рельефі атмосфераның төменгі
қабаттарында желдің пайда болуына себеп болады. Мұндай жергілікті желдер
ауа қозғалысының жылдамдығы болмағанда немесе ауа жылдамдығының 2-3 мс
аспағанда пайда болады.
Жел сонымен қатар векторлық өлшемдерді ұсынады. Оның мінездемесіне
жылдамдықпен қатар оның бағытын да міндетті түрде көрсету қажет. Сонымен
қатар, ауа ағынының жылдамдығы белгілі шарттарға сәйкес, яғни ауаның
қарапайым қабаттары мен орташа жылдамдықтарында, ауа ағысының ауысуы
жүретін турбулентті қозғалысы бар.
Метеостанцияларда желдің жылдамдығын және бағытын жер үстінен арнайы
i биіктікте 10 немесе 15 м –де, флюгердің көмегімен айқындайды. Өлшеулер
күніне 4 рет жүргізіледі.
Құрылғылармен қолдануға болмайтын жағдайда визуальды көрініс жүреді.
Сонымен қатар желдің жылдамдығы халықаралық метеорологтардың комиссиясымен
қабылданған Бофорт шкаласы бойынша есептелінеді. Бұл шкалада анемометрмен
өлшенген желдің жылдамдығы мен объективті белгілері қарастырылған (кесте-
1).

Кесте 1.2. Бофорт шкаласы.

Бофорт Желдің Толық мәлімет Жел жылдам-
балдары мінездемесі дығы мс
1 2 3 4
0 тымық Тұрбадан шыққан түтін вертикаль 0-0,5
көтеріледі;
1 тұнық Желдің бағыты флюгердің 0,6-1,7
қозғалысымен емес, түтіннін
бағытымен анықталады;
2 жеңіл Адам беті желді сезе бастайды; 1,83,3
Жапырақтардың сыбдыры естіледі;
флюгер қозғалады;
3 баяу Жапырақтар бірқалыпты қозғалыста 3,4-5,2
болады; жеңіл жалаушалар шайынады;
4 біркелкі Ауаға қағаз қалдықтары мен шаңдар 5,3-7,4
көтеріледі; жіңішке бұтақтар
тербеледі;
5 жаңа Кішкентай ағаш жапырақтары 7,5-9,8
шайқалады;
6 күшті Үлкен бұтақтар қозғалады; 9,9-12,4
Телеграфта желдің дауысы естіледі;
7 мықты Ағаштардың бұтақтары бірқалыпты 12,5-15,2
қозғалыста болады;
8 теңіз дауылыАғаш бұтақтары сынады; желге қарсы 15,3-18,2
жүрілмейді;
9 қатты теңіз Кіші мекемелерге зақым келеді, 18,3-21,5
дауылы тұрбалар құлайды;
10 теңіз дауылыАғаштар тамырымен қопарыла құлайды;21,6-25,1
үлкен мекемелерге зақым келеді;
11 қатал теңіз Үлкен қирату; 25,2-29,0
дауылы
12 ураган Алапат әрекеттер; 29.0

Жер бедерінің тегіс емес жерлерін ауа ағындарының орағытып ағуы.
Кедергілердің үстінен айналып өтуде ауа ағындарының 4 түрлі типі бар:
1. Ламинарлы ағын. Өте баяу жел соққанда байқалады. Тоқ
линиясының күрт өсуі оның формасын қайталануына әкеледі, соған байланысты
биіктік амплитудасының өсуі төмендейді. Кедергілерді айналып өтуде
ешқандай өзгерістер байқалмайды.
2. Иірім ағыны. Біркелкі қатты жел соққанда байқалады. Кедергілерге
жел соққан жағында горизонталь осьпен есептегенде иірімдер пайда болады.
Бұл иірім өзінің орнын ауыстырмайды. Тұрақты иірім болған кезде
кедергілердің үстіндегі ағын ауа ағыны бойымен араласады. Жел соққан
аймақтарда басты ағындарға қарсы ауа ағындары пайда болады.
3. Ағынның толқынды қозғалысы. Қатты жел соққан аймақтарда байқалады, жел
соққан аймақтарда иірімдер системасы бойынша стацианарлы иірім
жайылады.
4. Ротор ағыны. Өте қатты жел соққанда иірімдер тудырады. Толқын жүйесі
бұзылады және қозғалыс анықталмайтындай мазмұндар туындайды.
Экспериментальды мәліметтердің толықсыздығынан, кедергі үстіндегі
қандай да бір ауа ағынының айналу параметрін нақты анықтай алмайды.

1.3 Есептің қойылуы

Бұл курстық жұмыстың артықшылығы, шекаралық қабаттың қалыңдығын, жер
үстінен 5-10 м биіктіктен бастап атмосфераның жоғарғы қабатына дейін
алынуы, яғни жер бедері мен қаланың биік ғимараттарынан туатын кедергілерді
жалған облыстар әдісін қолдана отырып ескеру. Жұмысты зерттеу барысында:
- атмосфераның шекаралық қабатының теңдеуі жалған облыстар әдісі
арқылы шығарылады;
- теңдеулер жүйесіне алғашқы мәндермен шекаралық шарттарды койылады;
- атмосфераның шекаралық қабатының теңдеуінің сандық шешімінің
алгоритмі физикалық процесстерге жіктеу әдісімен іске асырылып белгілі
кезеңдермен іске асырылады;

2. АТМОСФЕРАНЫҢ ШЕКАРАЛЫҚ ҚАБАТЫНЫҢ САНДЫҚ ҮЛГІЛЕРІ

Атмосфералық процесстер жаратылыстану және антропогендік факторлар
мен әртүрлі кеңістік уақытша масштабтар бірігуінен туындаған әсерлер
нәтижесінде дамиды. Сондықтан да бір уақытта екі жағдайдың математикалық
моделін қалай құру керек деген сұрақ туындайды. Бір жағынан физикалық
процесстерің көп жақтылығы және кең спектрді есепке алу қажеттілігі.
Модельдердің физикалық мазмұны бойынша бай болуын, ал олардың
дискреттік аппроксимациялары жоғары кеңістік уақытша кеңейтілуін
қамтамассыз етуін талап етеді. Сонымен қатар бұл модельдерді есептеуіш
машиналарында эффективті нақтылау қажет. Атмосфера физикасының есептерін
шешуде бар тәжірибені есепке ала отырып, негізі етіп ылғал алмасу және
жердің термиялық пен орографиялық бірыңғай емес беткі қабатымен
атмосфераның өзара әсерлесуін есепке алғандағы адиабаталық емес
жуықтауындағы атмосфераның гидротермодинамикасының толық теңдеулер
жүйесімен сипатталатын модельдерді алған жөн. Активті факторлар қатарына ең
алдымен шектелген территориядағы ауа массасының фондық процесстерге әсері
және жылу, ылғал, әртүрлі қоспалар сияқты антропогенді жерлер және жердің
беткі қабатының динамикалық гидрометеорологиялық және жылу – физикалық
мінездемелерін жатқызуға болады.

1. Ақырлы айырымдар ұғымы

Ақырлы айырымдар ұғымын келесі сызықты гиперболалық теңдеудің
мысалында қарастырайық

,
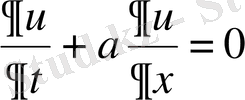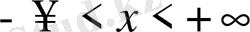(1.1)

мұндағы 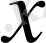кеңістіктік айнымалы, - уақыт, -
тұрақты.

Бұл теңдеудің шешімі жалғыз болуы үшін қандайда бір уақытында
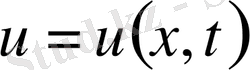функциясын анықтауымыз қажет. Сонымен қандайда бір уақытында

,
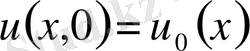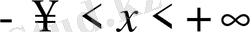(1.2)

болсын. Бұл теңдеу (1.1) үшін бастапқы шарт деп аталады. Ал (1.1)
-(1.2) есебі Коши есебі деп аталады.

Енді (1.1) - (1.2) Коши есебін сандық шешу үшін ақырлы-айырымдық схема
құруды қарастырайық. Сандық шешімнің аналитикалық шешімнен өзгешелігі,
сандық шешім 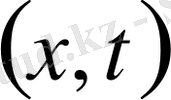жазықтығының қандай-да бір дискреттік нүктелерінде
табылады. Ох осінде келесі шексіз нүктелерді енгізейік

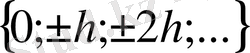(1.3)

мұндағы 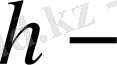қандай-да бір берілген оң шама. Бұл нүктелер жиыны
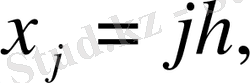
есептеу облысы немесе кеңістіктік тор деп аталады. 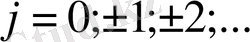нүктелері
кеңістіктік тордың тораптары деп аталады. 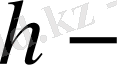шамасы кеңістіктік тордың
қадамы деп аталады.

Теңдеудің шешімі ақырлы 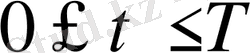, мұндағы берілген шама, ,
аралығында ізделінсін. (1.3) – ке ұқсас біз осінде де торды анықтай
аламыз:

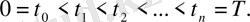(1.4)

Егер келесі шарттар орындалса (1.3) , (1.4) торлары бірқалыпты
торлар деп аталады:

;
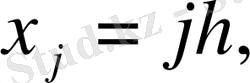
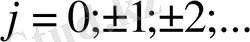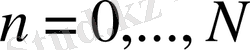(1.5)

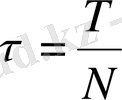шамасы уақыттық қадам деп аталады.

Енді 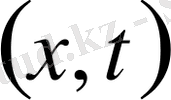жазықтығында торын келесі түзулердің қиылысу
нүктелері жиыны ретінде енгізейік:

; .

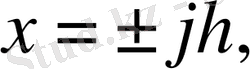
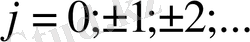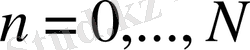Осы тордың түйіндерінде анықталған 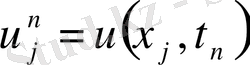функциясы торлық функция деп
аталады. Біз теңдеуді ақырлы айырымдар әдісімен шешкенде (1.1) - (1.2)
есебінің торындағы 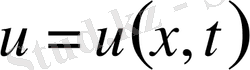шешімінің мәндерінің келесі таблицасын
табуымыз керек

.

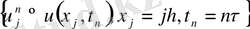Ақырлы айырымдық схема құрудың ең қарапайым әдісі осы теңдеудегі
дербес туындыларды ақырлы айырымдармен алмастыру. Біздің мысалда дербес
туындыларды келесі ақырлы айырымдармен алмастыруға болады:

;
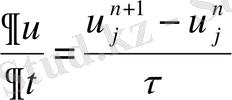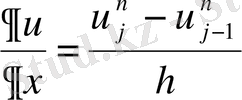(1.6)

Осы теңдіктерді берілген теңдеуге қойып, келесі айырымдық теңдеуді
аламыз

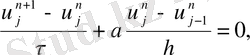
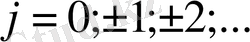
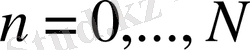(1.7)

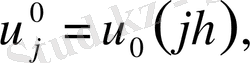
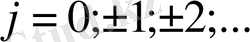(1.8)

(1.7) теңдеуі ақырлы айырымдық теңдеу деп, ал (1.7)-(1.8) есебі ақырлы
айырымдық Коши есебі деп аталады.

.

. 2.1 Гидростатикалық жуықтаудағы атмосфераның шекаралық қабатының
теңдеуі

Локальді масштабтың шектелген территориясындағы атмосфералық
процесстердің гидротермодинамикасының моделін қарастырайық. Теңдеуді жазу
үшін x, y, z, тікбұрышты координатасының сол жақ жүйесін қолданайық (х өсі
шығысқа, у- солтүстікке, z- вертикаль жоғары бағытталған) үзіліссіз күйдегі
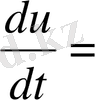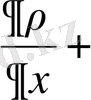
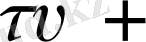
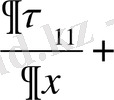
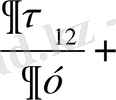
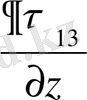-, (2.1)
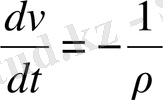
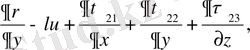(2.2)
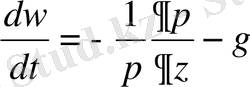(2.3)
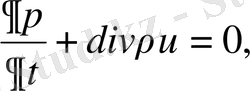
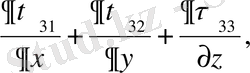(2.4)

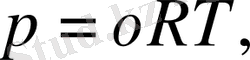(2.5)
жылу ағыны

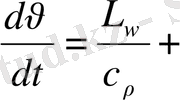
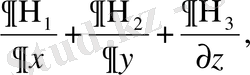(2.6)
салыстырмалы ылғалдылық
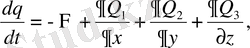(2.7)
онда
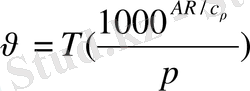
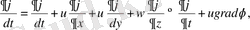(2.8)

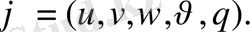
мұндағы t- уақыт, u, 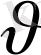, - сәйкесінше x, y, z декарт
координаталары бағытындағы жел жылдамдығы векторының компоненттері T-
температура, 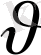- потенциалдық температура, р- қысым, q-бөлінетін
ылғалдылық, 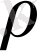- тығыздық, R- универсальды газдық тұрақты, -
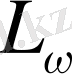конденсация жылуы, Ф- сұйық фазаның түзілу жылдамдығы, 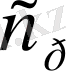- тұрақты
қысымдағы ауаның жылу сыйымдылғы, 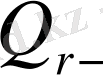жылу ағынының радиациялық құраушысы,
А- жұмыстың термиялық эквиваленті, g- еркін түсу үдеуі, L- Кориолис
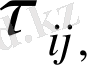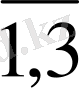параметрі, i=, j=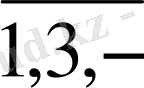Рейнальде кернеуінің тензоры,
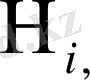
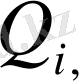i=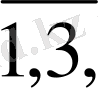- сәйкесінше x, y, z бағытындағы жылу және ылғалдылық ағыны. -
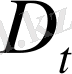облысында қарастыратын боламыз: DX[0, 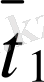], мұндағы D={x 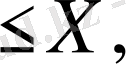y
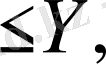0- кеңістік айнымалылардың өзгеру облысы, ал 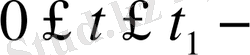уақыт интервалы.
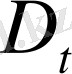- облысының өлшемдері кіріс параметрлері болып табылады. (1.1.1)-
(1.1.8) теңдеулер жүйесі жалпы жағдай үшін берілген, ол әртүрлі масштабтағы
атмосфералық процестерді процестерді есепке алады және де бұл теңдеулер,
жіктелу реттері бірдей емес. Сондықтан да нақты есептерді шешуде кейбір аз
мөлшердегі жіктелулерді қысқартуға болады. Мысалы: сызықты емес
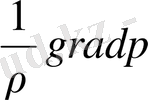түріндегі жіктелуін қарастырайық. Осы мақсатпен жаңа функция енгізейік,
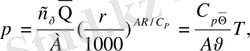(2.9)
мұндағы 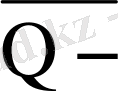потенциалдық температураның орта мәні (2.8).
Потенциалдық температура анықтамасын және функциясын қолданып
келесіні аламыз.
-
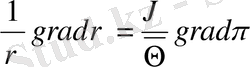(2.10)
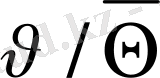1 болғандықтан, 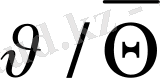=(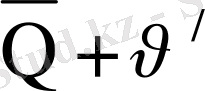), екенін ескеріп (2.1) –
(2.3) теңдеулер жүйесін келесі түрге келтіреміз:
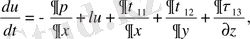(3.11)
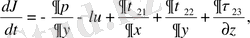(3.12)
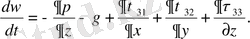(3.13)
Тығыздықтың, кеңістіктің – уақытша өзгерістерін өте аз деп ұйғарып,
(2.4) теңдеуін мына түрде жазайық:
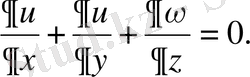(2.14)
(3.14)
Сонымен қатар атмосфералық қозғалыстарды квазистатикалық жуықтауда
қарастырумен шектелейік. Онда бастапқы теңдеуді мына түрде жазуға болады:

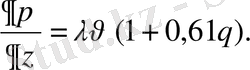(2.15)
Локальді атмосфералық қозғалыстар үшін келісімді теңдеулер жүйесін
алу үшін метеорологиялық жазықтықтар түрінде көрсетейік:
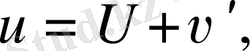
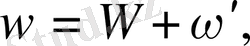
, (2.16)

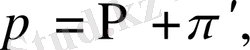
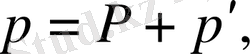
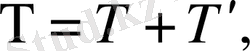
мұнда үлкен әріптермен метеорологиялық жазықтық, фондық ірі масштабты
қүраушылары, ал китрих бар әріптермен – ауытқулар белгіленген. (2.15)
өрнекті (2.16), (2.7) және (2.11) – (2.15) теңдеулеріне қоя отырып және
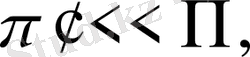
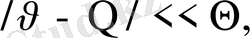ұйғаруы негізінде пайда болған өте аз
шамаларды есепке алмай, пайда болған теңдеуден фондық жазықтықтарға сйкес
келетін мезометефологияның ізделінді теңдеулер жүйесін аламыз. Енді
қарсылық теңдеулер жүйесіне негізделген атмосфераның орографиялық және
термиялық біртексіз сырғанақ бетіндегі шекаралық қабатындағы динамикалық
сандық моделін қарастырайық. Орографияның әсер етуін есепке алу үшін (x, y,
z) декарттық координаталар жүйесінен қисық сызықты жүйесіне ауысамыз:
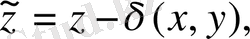(2.17)
мұндағы 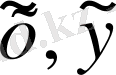өзара ортогональ және рельеф бойымен бағытталған, ал
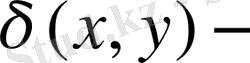рельефін сипаттайтын функция. Атмосфера өте аз деп ұйғарылған,
сондықтан х және у – ті тәжірибе жүзінде горизонталь координаталар деп
қарастыруға болады. Сол себепті u және 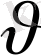ретінде жылдамдық векторының
горизонталь құраушыларын алуға болады. Бастапқыда ауа массасының Н биіктік
тұрақтысы болсын және оның төменгі бөлігі квазистационар h=h(x, y)
биіктіктегі жерге жақын қабатын білдіреді. Атмосфераның төсеніш бетімен
өзара әсерін жердің беткі қабатының моделі көмегімен сипаттайық, ал қабат
үшін жоғарыдағы ұйғаруларды есепке ала отырып, келесі теңдеулер
жүйесін аламыз:
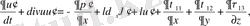(2.18)
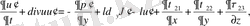(2.19)
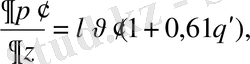(2.20)
(2.21)
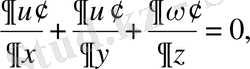(2.23)
мұндағы 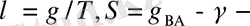конвекция және стратификация параметрлері, ылғалды
адиабаталық температура градиенті, 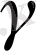- стандартты атмосфераның вертикаль
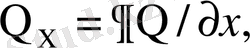
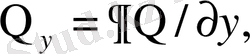
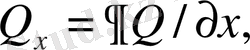
градиенті, 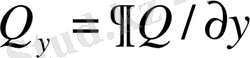- декарт координаталар жүйесіндегі
фондық потенциалдық температурамен бөлінетін ылғалдылықтың горизонталь
градиенттері: 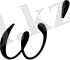шамасы жоғарғы ретті аз шамаға дейінгі дәлдікпен жел
жылдамдығы векторының 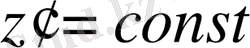координаталар бетіне нормаль құраушыларын
көрсетеді, (2.18) – (2.23) теңдеулеріндегі 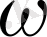вертикаль жылдамдығы
декарт координаталар жүйесіндегі 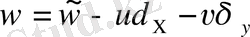қатыстағы 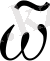вертикаль
жылдамдығымен байланысты.
Осылайша модельге фондық потенциалдық температура мен бөлінетін
ылғалдылықтың горизонталь градиентінің әсері енгізіледі, немесе басқаша
айтқанда фондық ағынмен, жылумен ылғалдылық адвекциясы есептеледі. Нақты
көрсеткіштермен жүргізілген бақылаулардың анализ нәтижелері, мұндай
адвекциялар әсерінің заттық болуы да мүмкін екендігін көрсетеді.
Горизонталь бойынша шектік шарттар шешімінің Экман моделіне немесе Прандатл
жел моделінің шығуына мүмкіндік береді.

2.3 Гидростатикалық емес жуықтаудағы атмосфераның шекаралық
қабатының теңдеуі

Жоғарғы тегіс емес қабаттарды ескере отырып атмосфераның шекаралық
қабатын анықтау мақсатында, математикалық үлгілеудің мезометрологиялық
процесстерін қарастырайық. Ол үшін атмосфераның турбулентті шекаралық
қабатының термогидродинамикалық теңдеулер жүйесіне оралайық. Солтүстік
жарты шар үшін ең ортақ жорамал кезінде бастапқы мәндер үшін келесі
теңдеулерді қарастырайық:
1) қозғалыс теңдеуі

,
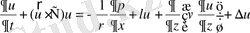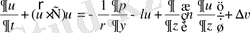, (2.1.1)
,

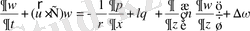2) үзіліссіздік теңдеуі

,
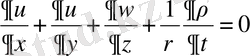(2.1.2)
3) күйін анықтайтын Клапейрон теңдеуі

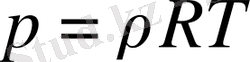
(2.1.3)
4) жылу ағысының теңдеуі

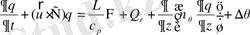, (2.1.4)

5) потенциалды температура үшін теңдеу

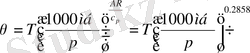, (2.1.5)

6) бу тәрізді ылғал үшін теңдеу

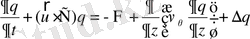, (2.1.6)

7) сұйық үшін тамшы тәрізді сұйық фазаның теңдеуі

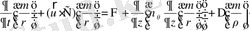. (2.1.7)

Мұнда 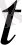- уақыт; 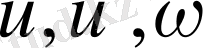- сәйкесінше 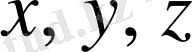декарт координаталары
бағытындағы жел жылдамдығы векторының компоненттері; -температура;
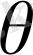- потенциальды температура; - қысым; - тығыздық; -
универсальды газдық тұрақты; - буланудың жасырын жылуы; - сұйық
фазаның түзілу жылдамдығы; 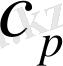-ауаның тұрақты қысым кезіндегі меншікті
жылу сыйымдылығы; - жылу ағынының радиациялық құраушысы; -
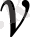турбулентті ағымның вертикалды коэффициенті; 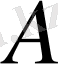- жұмыстың термиялық
эквиваленті; 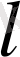- Кориолис параметрі; - сұйықтық. Сонымен қатар
қатынаушы операторлар келесі түрде өрнектеледі:

; .

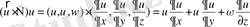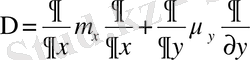Мұнда 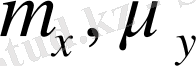- турбулентті ағымның горизонталь коэффициенттері.
Тегіс емес жерлерді есепке ала отырып, атмосфераның шекаралық
қабатының қозғалысын анықтау мақсатында аз мөлшерде әсер ететін
қосылғыштарды алып тастаймыз, сонымен қатар қарапайымдылық үшін ылғалды
есептемейміз.
(2.1.1)-(2.1.7) теңдеулер жүйесі мезометеорологиялық құбылыстардан
басқа дыбыстық қысқа толқындарды, үлкен масштабты метеорологиялық
процесстерді және басқа да мезометеорологиялық шуларды суреттейді. Осы
теңдеулер жүйелерін тұтастай қарастыру тиімсіз болып келеді. Себебі жүйенің
барлық мүшелерінің мәндері біртекті болып келмейді.
Көптеген осындай жұмыстарда мезометеорологиялық есептерде шешу
кезінде метеорологиялық параметрлерді өзгерген және өзгермеген өрістерге
келесі түрде бөліп қарастырады.
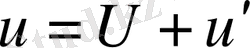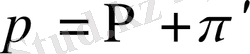, , , , (2.1.9)
Ал, жергілікті жерлерде метеорологиялық параметрлерді өзгерген және
өзгермеген өрістерге бөлу үлкен масштабты мезометеорологиялық есептерде
болмаса, жергілікті жердің атмосфералық құбылысын зерттеуде тиімсіз болып
келеді. Себебі ауа ағысының өзгермеген өрістерінің әсерінен өзгерген
өрістерді бағалау мүмкін емес болады. Сол себепті бұл ғылыми жұмыста
өзгерген өрістер ғана қарастырылып, өзгермеген өрістер шекаралық және
бастапқы шарт ретінде ескеріледі.
Өлшем бірліксіз қысым келесі түрде анықталады:

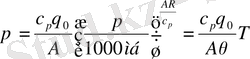(2.1.8)
мұнда 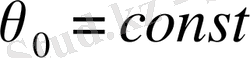- потенциальды температураның орташа мәні. Онда (2.1.1)-(2.1.7)
теңдеулер жүйесі келесі түрде болады:
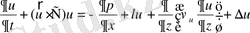, (2.1.9)
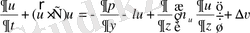, (2.1.10)
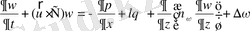, (2.1.11)
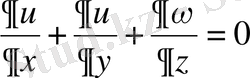, (2.1.12)
, (2.1.13)
мұнда 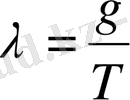- конвекция параметрі, 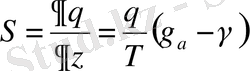- стратификация параметрі, -
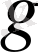еркін түсу үдеуі, 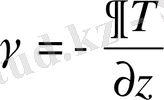- стандартты атмосфера температурасының вертикалды
градиенті, 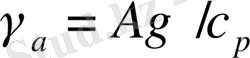- құрғақ адиабаталық градиент.

2.1.1 Бастапқы және шекаралық шарттардың қойылуы

Бастапқы және шекаралық шарттардың қойылуы әрбір есептің
ерекшелігіне сәйкес негізделеді. Көп жағдайда мезометеорологиялық есептерді
шешу кезінде шекаралық аймақтардағы процесстерді дәл суреттеу немесе
мәндерін тауып қою қиындық туғызады. Себебі қарастырылып отырған шекаралық
аймақ тұйықталмаған еркін аймақ болып келеді. Мұндай жағдайларда әдетте
еркін айналу шарттары қойылады, мысалға нормаль бағыттағы вектордың
градиенті нөлге тең деген шекаралық шарт қойылды. Ол ішкі ағымды шекарада
тура бейнелейді.

Бұл дипломдық жұмыста атмосфераның шекаралық шарттарын үлгілеуде
әртүрлі жағдайлар қарастырылған, себебі ауа ағындарының жалпы табиғаты
стационарлы емес және әрдайым қозғалыста болады.

болғанда атмосфераның шекаралық қабаттарының бастапқы шарты
келесі өлшемдер бойынша беріледі, сонымен қатар кіру параметрлерінің
сандарына кіреді. Аудандардың физико-географиялық климаттық мінездемелеріне
байланысты нақты есептерді шешуде төмендегідей бастапқы шекаралық шарттарды
қолдану тиімді:

, , , (2.1.14)

мұнда нақты атмосфераның өлшемдерімен анықталады. Тегіс емес жерлерді
ескере отыра (төбешіктердің биіктігі, аңғалдардың немесе сайлардың
тереңдігі) ауаның температурасы биіктік бойынша азаяды, яғни
метеорологиялық курсыдан белгілі, тропосфера қабатында температура, қысым
және тығыздық биіктік бойынша кемиді. Температура жуық шамамен 100 м –де
.

Кірістегі қырдың шекарасына уақыт бойынша фондық желдің өзгерісі
ретінде келесідей шекаралық шарттарды қолдануға болады.

, , , при

, , , при (2.1.15)

мұнда функциялар , берілген өлшемдермен ескеріледі. Ал шығыстағы
қырдың шекарасына жанама құрылғандарға өзгермеген ағынның шарттары қойылады
А на выходах боковых границ ставятся условия невозмущенных потоков для
касательных составляющих, а невозмущенное ускорение для нормальных
составляющих.

Мұндай қойылған шекаралық шарттар уравнения неразрывности шарттарын
орындалуын қамтамасыз етеді, сонымен қатар бос шекараларға жылдамдық пен
желдің бағытын сақтауға мүмкіндік береді.

, , при

, , при (2.1.16)

Шекаралық шарттар (2.1.16) графикалық түрде төмендегі 2.1.-суретте
айқын көрсетілген.

2.1 - Сурет – Оңтүстік-шығыс бағыттымен соққан желдің шекаралық
шарттары

Көптеген жұмыстарда [5, 8, 41, 60] жылдамдықтардың барлық
компоненттерінде өзгермеген ағынның шарттары қойылады немесе тек қана
орташа құрылғандарға жұмсақ шекаралық шарт қойылады, ал жанама
құрылғандар нолге тең болады. Мұндай шарттардың қойылуы негізінен дұрыс
болып саналмайды. Мысалы, бірінші жағдайда шекараларда неразрывность
теңдеуі орындалмайды. Оның орындалуы үшін келесілерді дәлелдеуіміз қажет,
яғни сәйкес бағыттағы қарастырылып отырған шекарада әрбір компоненттің
градиенті нөлге тең болуы қажет, ал екінші жағдайда мұндай кемшіліктер жоқ,
бірақ қарастырылып жатқан шекарада ағынның бағыты нормальдың бағыты
бойынша түзеледі.

Егер желдің бағыты сәйкес келіп немесе координат осінің горизонталь
бағытымен сәйкес келмейтін болса, онда сәйкес келетін шеткі шекараларға
сырғанау шарттары төмендегідей қойылады:

, , (2.1.17)

Мұнда , - Облыстың шеткі қырларының шекарасындағы жылдамдықтың
нормаль және жанама компоненттерінің мөлшері.

2.2-сурет –шығыстан соққан желдің шекаралық шарттары

Енді төменгі және ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.