Компьютерлік модельдеу
Мазмұны
Кіріспе
Курстық жобаның мақсаты - «Экономикалық және өнімдік процесстерді модельдеу» курсты оқыту процессінде студенттермен алынған білімді бекіту мен тереңдету, нақты оптимизационды есептерді шешуінде өздік жұмысының біліктілігін дамыту, математикалық программалау есептері үшін компьютерлік программаларды меңгеру мен практикалық қолдану.
Компьютерлік модельдеу - бұл ақпараттық тәртіптердің циклындағы жаңа және күрделі бағыт.
Компьютерлік модельдеу табысты игеруіне әр түрлі саланы жақсы білу қажет: - біріншідең, таңдап алынған сала облысында - егер біз физикалық процесті модельлесек, физикалық заңдардаң белгілі бір білім деңгейі болу керек, экология процесті модельлесек - биология заңдылықтарын, экономика процесті модельдеуде - экономика саласынан білімді болу керек, сонымен қатар компьютерлік модельдеуде математиканың барлық саласы қолданылады, негізгі математиканың пәндерін білу керек - алгебра, математикалық негіз, дифференцалдық теңдеулер теориясы, математикалық статистика ықтималдық теориясы.
Математикалық есептерді компьютерде шығару үшін теңдеулердің сандық әдістерімен толық көлемде таныс болу ұзындық теңдеулердің жүйелерінің, дифференциалды теңдеулердің, функциялар аппроксимациялау және интерполяциялауға білу қажет.
Және де қазіргі заманға сай ақпараттық технологияларды еркін колдана білу, бағдарламалау тілін білу және қолданбалы бағдарламаларды өңдеуді игеру.
1 Жалпы бөлім
1. 1 Компьютерлік модельдеу
Компьютерлік модельдеу, математикалық модельдеудің бір бағыты ретінде компьютерлік технологиялардың дамуымен компьютерлердің қолданудың дербес және маңызды облысы болып қалыптасты. Қазіргі кезде компьютерлік модельдеуге ғылыми және практикалық зерттеулерді танудың негізгі әдістерінің бірі болып табылады.
Ірі ғылыми және экономикалық мақсаттарды - компьютерлік модельдеудің көмегісіз шешу мүмкін емес. Қарастырып жатқан объекті есептеуіш техниканын матемтикалық модельс арқылы Күрделі проблемалардың зерттеу технологиясы істеп шығарылған.
Зерттеудің осындай әдісі есептеуіш тәжірибиесі деп аталады. Есептеуіш тәжірибе ғылымның барлық дерлік саласында қолдалынады - физика, химия, астрономия, биология, экология, сондай - ақ психология, филология, лингвистика сияқты гуманитарлық ғылымдарда қолдалынады. Ғылыми облыстар басқа есептеуіш тәжірибелер экономика, социология, өнеркәсіп басқаруында кеңінен қолданылады.
Өткізілген есептеуіш тәжірибе табиғи тәжірибеден бірқатар артықшылықтары болады:
- Есептеуіш тәжірибе үшін күрделі лабораториялық жабдықтаудың қажеті жоқ;
- Тәжірибе аз уақыт ішінде жасалынады;
- өз бетіменді олардың басқару мүмкіншілігі, параметрлермен өзгертудің, әр түрлі мағыналар беруге болатындығы;
- Есептеуіш тәжірибенің ыңғайлылығы табиғи тәжірибені өткізе алмайтын жерлерде өткізу мүмкіншілігі болады, қайда - бір кеңістікте зерттейтін құбылыстың қашығына байланысты (астрономия), немесе оның уақытының ұзақтылығынан байланысты (биология), немесе оқылатын процес қайтарымсыз болатын болса.
КМ осы жағдайларда қолдалынады. Сонымен қатар бірім беру және оқу процесінде КМ кеңінен қолданылады.
КМ табиғи ғылымды оқуда барабар келеді. КМ оқу информатика мен математиканың және басқа әлуметтік және табиғи ғылымдармен байланысын көрсетуге мүмкідік ашады.
Модельдеудің ұғымы - өте кең ұғым, ол тек қана математикамен модельдеумен шектелмейді.
Модельдеу элементтері жиі балаларларын ойындарда кездеседі, балалардың сүйікті жұмысы - қол астындағы заттармен үлкен адамдардың өмірдегі қатынастарына модель жасайды. Балалар бой жетеді, адамзат есйеді.
Адамзат қоршаған ортаны тани бастайды, нақты объектілермен сыртқы ұқсастықтығын жоғалтып модельлер абстракты бола бастайды. Зерттеулер нәтижесінде анықталғандай, модельлердің терең заңдылықтары бар.
Модельлердің ролінде әр түрлі объектілерді алуға болады: бейнелеулер, схемалар, карталар, графикалар, компьютерлік бағдарламалар, математикалық формулалар және т. б.
Егер біз математикалық формулалармен нақты объектіні ауыстырсақ ( ньютон 2 заңы мүмкін, сәйкес, жүйемен - дененің қозғалысын сықтық емес теңдеумен сипаттайық, немесе жылу өткізгіштік заңына сәкес жылудың таралуын 2 - ші реттік дифференциалдық теңдеумен сипаттайық) оны математикалық улгілеу деп атайда, сол сияқты егер нақты обектерді компьютерлік бағдарламамен алмастырсақ - оны компютерлік модельдеу деп атайды.
Модельлер ролінде қандай обект болса да, модельдеу объектіні зерттеу арқылы нақты объектінің өгеру процесін бақылап оның қасиеттері туралы ақпататты жіберу болып табылады.
Осы процес модельдеу деп аталады. Орны алмасушы объекті түпнұсқа деп ал, орнын басушы - модель деп аталады.
Компьютерлік модельдеу технологиясында келесі негізгі ұғымдарды ерекшелеуге болады.
Модель - жасанды жасалған объекті, нақты объекті - түпнұсқасын айқын түрде көрсетеді.
Компьютерлік модель - модель жүйесі туралы компьютерлік құралдарымен ұсынуы.
Жеке элементтердің қасиеттерінен өзгеше қасиеті бар өзара байланысқан элементтерді - жүйе деп атайды.
Элемент - модельдеу мақсаттарына арналған маңызды қасиеттері бар объекті.
Компьютерлік модельде элемент қасиеттері элемент мөлшерлермен - мінездемелерімен беріледі.
Элементтер арқасындағы байланыс мөлшерлер және алгоритмдер арқылы сонымен қатар есептеуіш формулалардың арқылы сипатталады.
Жүйенің күй-жағдайы элементтер арасындағы байланысты және компютерлік модельдің элементтерінің мінездеме топтарымен көрсетіледі. Берілгендердің құрылымын сипаттайтын күй - жағдай нақтылы күй-жағдайға тәуелді болмайды және күй-жағдайлардың ауысуында өзгермейді тек қана мінездемелердің мағынасы ғана өзгереді.
1. 2 Модельдеу түрлерінің классификациясы
Пәндік және абстрактты модельдеу түрлерін айырады.
Пәндік модельдеуде физикалық моделін салады, бейне негізгі физикалық қасиеттер және модельденуші объекті мінездемелерін суреттейді.
Осы жағдайда да модель модельденуші объектімен салыстырғанда физикалық табиғаты басқа бола алады.
Егер модельдің және объектің физикалық табиғаты бірдей болса, онда бұл модельді физикалық модельдеу деп атайды.
Осы кезге дейін күрделі техникалық объектілерді жасауда физикалық модельдеу кең қолданылды.
Объектке қоятын талапты орындау үшін - әдеттегі макеттік немесе техникалық объектің тәжірибелі модельді дайындалып, оған сынау өткізіледі, осының барысында оның шығатын параметрлері және мінездемесі қайсылардың, жұмыс жасау сенімділігі және техникалық талаптардың орындалу дәрежесі бағаланды.
Егер қойылған мақсат орындалмаса, онда барлығын қайтадан жасайды, яғни модельнің бұл түрі уақыттық және материалдық шығындарға ұшырайды
Пәндік модельдеуді басқа жағынан да қарастыруға болады. Бар физикалық табиғаттың
Әртүрлі құбылыстары көптеген ұқсас сандық заңдылы болады және осылардың бәр бір математикалық аппараттың көмегімен ған анықталады. Бұл жағдай кейбір құбылыстың сандық сипаттауды, процесті тіптем басқа физикалық табиғатпен зеттеуді мүмкін етеді. осындай әдіс модельдеуге ұқсас деп аталады.
Сондай жақын келу аналогтық модельдеумен аталады, ал негізгі процестің модельдеу басқа физикалық механизім - аналогтік модель арқылы іске асады.
Абстракты модельдеу абстракты модельді құрумен байланысты. Осындай модель графтардың, схемалардың, диаграммалардың матиматикалық қатынасын көрсетеді.
Математикалық модельдеу ең қуатты және әмбебаб абстракты модельдеу болып табылады.
Матиматикалық модельдеу математикалық символдардың және тәуелділіктердің көмегімен, болып жатқан процестерді суреттеуге мүмкіндік береді.
Математикалық модель - бұл математикалық объектілердің жиынтығы және олардың арасындағы қасиеттері және зерттейтін объектінің мінез-құлығын бейнелейтін қатынас.
Егер зерттелген қасиеттері қабылдауға болатын дәлдікпен көрінсе, модель барабар болып есептеледі.
Дәлдік - модельде есептеу тәжірбиесі кезіндегі анықталған мағыналардың нағыз мағыналармен сәйкес келу дәрежесімен анықталады.
Математикалық объектілер ретінде сандарды аламыз, айнымалылар, жиындар, векторлар, матрицалар және т. б.
Математикалық модельді құру процессі және оны талдауға және синтездеуде қолдану математикалық модель деп аталады.
Зерттеулерді осындай модельде өткізу есептеуіш тәжірибесі деп атайды.
ЭВМ - де есептеуіш тәжірибені жүргізу үшін математикалық модельдің орындау алгоритмын өндіру қажет.
Алгоритм - есептеуіш процесс операцияларының орындалу тізбектілігін анықтайтын алдын - ала жазылу.
Формада жазылған алгоритмді есептеуіш машина, бағдарламалық модель ретінде қабылдайды. Бағдарламалау процесі бағдарламалық модель деп атайды.
Математикалық модель дифференциалды теңдеулер жүйесін (кәдімгі немесе жеке туындылар), алгебралық теңдеулер жүйелерін, қарапайым алгебралық теңдеулерді, бинарлық қатынас, матрицалар және т. б.
Күрделі модель есептеуіш тәжірибелердің өткізуіне уақыттардың үлкен шығындарының талап етед.
Осындай модельдердің дәрежелері келісулері жаман болады, осы жағдай есептеу процесіне қамтамасыз етуіне уқытты жіберу кезіндегі дәлдігі қиындық тудырады.
2 Негізгі бөлім
2. 1 Курстық жобаға тапсырма
1. Симплекс-әдісі
F= 900x
1
+1100x
2
+1500х3 → max,
x
1
+2x
2
+4х
3
≤ 360.
2x
1
+4x
2
+2х
3
≤ 250,
x
1
+x
2
+2х
3
≤ 220.
x
1
, x
2
, х
3
≥ 0.
2. Геометриялық шешім
F= x
1
+0, 25x
2
→ max,
x
1
+2x
2
≤ 10,
3x
1
+2x
2
≤ 18,
x
1
-x
2
≤ 10,
2x
1
-x
2
≤ 19,
x
1
, x
2
≥ 0.
3. Транспорттік есеп
2. 2 Симплекс-әдісі
F= 900x
1
+1100x
2
+1500х3 → max,
x
1
+2x
2
+4х
3
≤ 360.
2x
1
+4x
2
+2х
3
≤ 250,
x
1
+x
2
+2х
3
≤ 220.
x
1
, x
2
, х
3
≥ 0.
Симплекстік әдісі . Сызықты программалау есептерін шешудің симплекстік әдісі бір опорлық жоспары екіншіге өтуде негізделген, бұл жерде мақсаттық функцияның мәні өспелі болады.
Қарастырылған ауысу мүмкін болады, егер қандай-да бір ізделінді опорлық план белгілі болса.
Егер ізделінді опорлықты анықтағаннан кейін бастапқы деректер мен есептің шарттын кесте түрінде көрсетсек, онда есептеу процессін және тиімділікке зерттеулерді жүргізуді ыңғайлы болады.
Бұл кестенің Сб бағанында берілген базистің векторының индекстеріне ие болатын мақсатты функцияның белгісіздерінің коэффициенттері жазылады.
P 0 бағанында ізделінді опорлық жоспарының оң компоненттері жазылады, осы жерде есептеулер нәтижесінде тиімді жосарының жақсы компоненттерін алады.
Iитерацияның симплекстік кестесін құрастырамыз, z j -c j , F 0, мәндерін есептейміз және ізделінді опорлық жоспарын тиімділікке тексереміз.
Кесте 1.
1 кестенің 4 қатарынан z 1 -c 1 =-900, z 2 -c 2 =-1100. z 3 -c 3 =-1500үш теріс сан бар екені анық.
Теріс сандар өңделетін өнімнің жалпы бағасысының артту мүмкіндігін дәлелдеуі мен қатар жоспарға өнімнің қандай да бір бірлігін ендіруінде бұл сома қаншалықты өсетінің көрсетеді.
Абсолютті шамасы бойынша максималды теріс сан
i
- Р
3
вектор бағының 4-ші қатарында тұр.
Сондықтан базиске Р 3 векторын енгіземіз. Базистен шығаруға тиіс векторды анықтаймыз. Ол үшін a i3 >0 үшін min(b i /a i3 ) табамыз, яғни min(360/4; 250/2; 220/2) =360/4.
Осы жерден Р 4 векторы базистен шығаруға жатады. Р 3 векторының бағаны және 1-ші қатары бағыттаушы болып саналады.
II итерацияның кестесін құрастырамыз (кесте 2. )
Кесте 2.
2 кестенің 4-ші қатарынан z 1 -c 1 =-525, z 2 -c 2 =-350 екі теріс сан бар екенің көрініп тұр.
Абсолютті шамасы бойынша максималды теріс сан
i
- Р
1
вектор бағының 4-ші қатарында тұр.
Осы жерден Р 1 векторын базиске енгіземіз. Базистен шығаруға тиіс векторды анықтаймыз.
Ол үшін a i1 >0үшін min(b i /a i1 ) табамыз, яғни min(90/(1/4) ; 70/(3/2) ; 40/(1/2) ) =70/(3/2) .
Осы жерден Р 5 векторы базистен шығаруға жатады. Р 1 векторының бағаны және 2-ші қатары бағыттаушы болып саналады.
III итерацияның кестесін құрастырамыз (кесте 3. )
Кесте 3.
3 кестенің нәтиесінде жаңа опорлық жоспарын аламыз Х=(0, 140/3, 235/3, 0, 0, 50/3)
Берілген опорлық жоспарының тиімділігін тексереміз. Ол үшін 4 кестенің 4 қатарын қарастырамыз.
Бұл қатарда теріс сандар жоқ екені анықталды. Сондықтан табылған опорлық жоспар тиімді болып саналады.
2. 3 MS Excel ЭК көмегімен есепті симплекс - әдісімен шешу
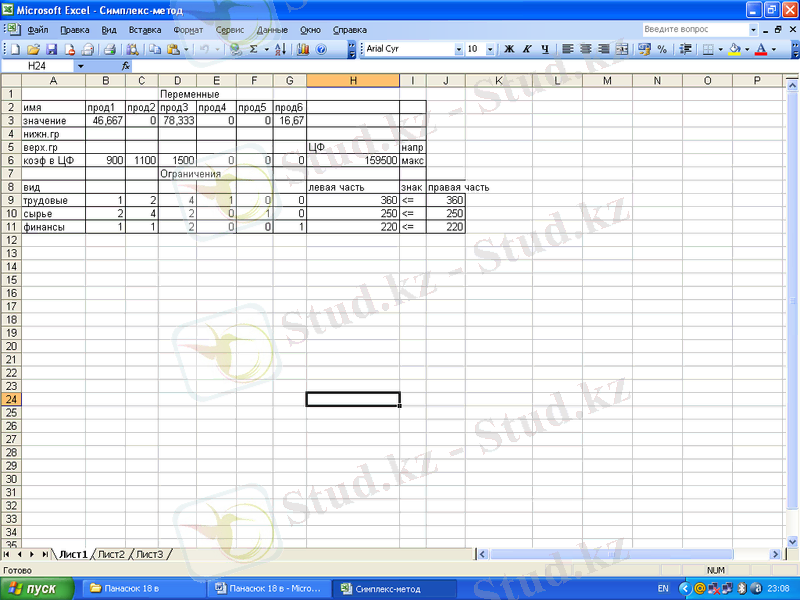
Сурет 1, 2 - MS Excel ЭК көмегімен есепті симплекс - әдісімен шешу
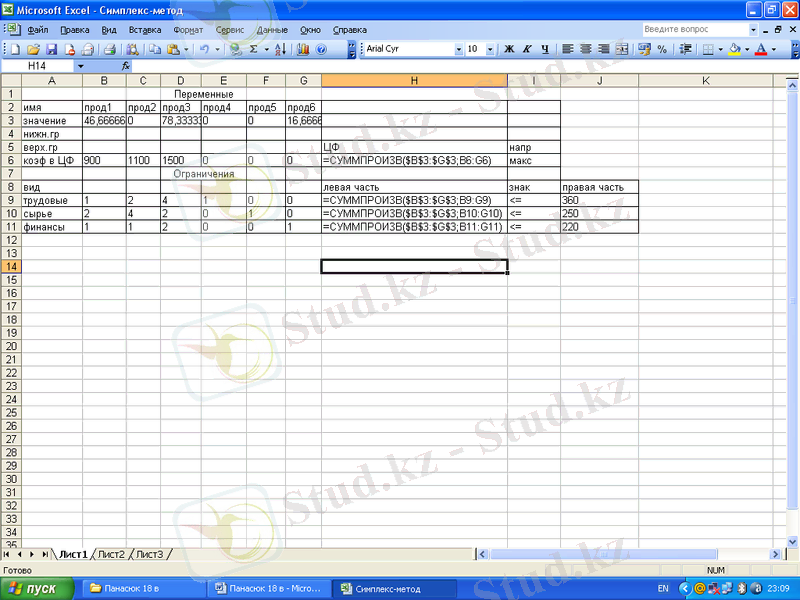
Сурет - 2
2. 4 Геометриялық шешімі
F= x
1
+x
2
→ max,
x
1
+2x
2
≤ 10,
3x
1
+2x
2
≤ 18,
x
1
-x
2
≤ 10,
2x
1
-x
2
≤ 19,
x
1
, x
2
≥ 0.
Геометриялық шешімін табу үшін теңдеу таңбаларын теңдік таңбаларға ауыстыру қажет:
I теңдеу x 1 +2x 2 = 10
II теңдеу 3x 1 +2x 2 = 18
III теңдеу x 1 -x 2 = 10
IV теңдеу 2x 1 -x 2 = 19
Содан кейін түзулер құрастырылады:
- x1+2x2= 10
х 1 =0 теңестіреміз, сонда х 2 =5
х 2 =0 теңестіреміз, сонда х 1 =10
(0; 5), (10, 0) координаталарымен түзу шығады
- 3x1+2x2= 18
х 1 =0, х 2 =9
х 2 =0, х 1 =6
(0, 9), (6; 0) координаталарымен түзу шығады
- x1-x2= 10
х 1 =0, х 2 =-10
х 2 =0, х 1 =10
(0, -10), (10; 0) координаталарымен түзу шығады
- 2x1-x2= 19
х 1 =0, х 2 =-19
х 2 =0, х 1 =8
(0; -19), (8; 0) координаталарымен түзу шығады
С(С
1
, С
2
) векторын құрастырамыз. С
1
, С
2
координаталары - бұл мақсаты функцияның х
1
және х
2
-дегі коэффициенттері, яғни С
1
=1, С
2
=0, 25. L
С шартында L деңгейлі түзуін құрастырамыз және жазықтықты векторға жылжытамыз. Минимум нүктесі I және II түзулер қиылысуында орналасады. Бұл нүктенің координаталарын табу үшін теңдеулер жүйесін шығару керек.
I теңдеу x 1 +2x 2 = 10
II теңдеу 3x 1 +2x 2 = 18
бұл жерден x1 =4, x2 =3. Минимум нүктесі (4; 3) координаталарына ие.
2. 5 Транспорттік есеп
Солтүстік - табыс бұрышының әдісі
Солтүстік - табыс бұрышының әдісімен транспорттік есептің опорлық жоспарын табу кезінде әр қадамында жіберу пункттерінің біріншісін және келу пәнкттерінің біріншісін қарастырады.
Шарттар кестесінің торларын толтыру x11 белгіссіз үшін сол жақтағы жоғарғы ұяшығынан және xmn белгіссіз үшін аяқталады, яғни солтүстіктен табысқа кестенің диагоналімен жүреді.
Есеп.
Берілген транспорттік есебінің тасымалдау жоспарын солтүстік - табыс бұрыштың әдісімен табу.
Шешімі.
Алдымен қорлар қажеттіліктерге теңдігін. Берілген есепте қорлар 600бірлікке және де қажеттіліктер де 600 бірлікке тең болады.
Бұл жерде жіберу пункттер саны m=3, ал келу пункттер саны n=4 тең. Сондықтан, есептің опорлық жоспары 3+4-1=6 толтырылған ұяшықтарда тұрған сандармен анықталады.
Кестенің толтыруын x 11 белгіссізден бастаймыз, яғни жіберудің бірінші пункт қорларының негізінде келудің бірінші пунктінің қажеттіліктерін қанағаттандыруға тырысайық. A 1 пунктінің B 1 қорлары пунктінің қажеттіліктерінен арттық болғандықтан, x 11 =120 деп болжамдаймыз, осы мәнді кестенің сәйкес ұяшығына жазамыз және A 1 пунктінің қорлары 80 бірлікке тең деп ұйғарып қарастырудан В 1 пунктін алып тастамаймыз. Содан кейін В 2 пунктін қарастырамыз, оның қажеттіліктері 80 бірлікке тең, x 12 =80 ұйғарып A 1 және В 2 пункттерін қарастырудан алып тастамаймыз.
... жалғасыСіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.
Ақпарат
Қосымша
Email: info@stud.kz