Моделдерді есептеу әдістері

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 15 бет
Таңдаулыға:

Мазмұны
Кіріспе
1. Жалпы бөлім
. Пәндік аумақты сипаттау
. Моделдерді құрастыру. Олардың түрлері.
. Моделдерді есептеу әдістері.
2. Арнайы бөлім
. Ойындар теориясының негізгі түсініктері және анықтамалары
(2x2), (2хn) және (mх2) түріндегі қарапайым ойындарды шешу Аралас
стратегияны қолдану
Қорытынды
Қолданылған әдебиеттер тізімі
Қосымшалар

Кіріспе

Студенттер курстық жобаны орындау барысында өзі ғылыми-техникалық
әдебиеттермен жұмыс істеп, қолданбалы тапсырмаларды орындау керек. Қазіргі
замандағы технологияға сай бағдарламалау жасап, бағдарламалық құжаттарды
стандарттық талаптар бойынша өңдеп, өз жұмысының нәтижелерін көрсету
мақсатында аудитория алдында қорғауы тиіс.
Курстық жоба студенттерді күрделі есептерді шешуге және дипломдық жоба
жазуға көмектеседі.
Менің курстық жобамның тақырыбы ойындар теориясы, аралас стратегия.
Курстық жобаны орындау барысында математикалық есептерді құрау үшін
модель таңдауы қажет, ЭЕМ машинасының көмегімен зерттелген немесе өзіндік
қаралған тәсілдер көмегімен қорытындыға келеді, сосын нәтижелерді анализін
жүргізіп, соңынан түсіндірме жазбаны өңдейді.
Экономика саласында басқару есептерін шешу кезінде өндіріс шараларында
әрдайым ауыспалылығын сипаттайтын ауыспалы шаманы ескере отыру керек.
Экономикада және басқарудағы есептерді шығаруға арналған, қазіргі
кездегі математикалық әдістердің аппараттары, өздігінен дамыған ғылымға
және қолданбалы аймаққа айналды. Дегенмен де, қолданбалы математикалық
әдістерді оқып, үйренуде күнделікті өмірде жиі қолдануды қалыптастыруда
көптеген қиыншылықтар мен түсініспеушіліктер кездеседі. Халық
шаруашылығының көптеген мамандары математикалық әдістердің өзекті мәнісін
әлі де болса дұрыс түсінбейді де, олардық қажеттілігін және осы әдістер
арқылы әр істе кереметтей нәтижеге жетуге болатынын көп сезінбейді. Осы
айтылғанның дәлел ретінде мынадай мәселеге көңіл аударайық. Мысалға,
кейінгі кезде Республикамыздың көптеген жоғарғы оқу орындарында қолданбалы
математикалық пәндер халық шаруашылығының әр саласы мамандарын дайндауға
арналған мемлекеттік стандарттарға бірде енгізіліп, бірде алынып
тасталынады немесе өте аз сағат бөлініп, факультативтік пән ретінде
жүргізіледі. Сонымен қатар, қазіргі компьютерлік техника мүмкіншілігінің
өсуіне және көптеген қолданбалы математикалық әдістері бойынша компьютерге
арналған қолданбалы программалар пакеттері жасалуына байланысты олардың
математикалық аппаратары, яғни есепті шығару алгоритміндерін оқып, терең
түсіну қажет емес деген сөз де жиі айтылады.
Адамның жасаған көптеген жұмыстарына байланысты өмірде өзінің кәсібі
бойынша әр түрлі құралдарды қолдана алатын адам әмбебап тәсілдерді
меңгерген адамға қарағанда, артық нәтижеге жетеді. Мысалыға бірде ойша
немесе қағазға жазып, ал үшінші жағдайда – компьютер арқылы, төртіншіде
арнайы бағдарлама арқылы оптималды есептеулер жүргізген тиімді болуы
мүмкін. Сондықтан әмбебап және жекелеген тәсілдерді білу мен қолдана алу
тез әрі оңай қойылған мақсатқа жеткізеді. Сөйтіп тәжірибелік есептерді
математикалық әдістермен шығару алгоритмдерін білу және қолдана алу,
есептің мәнісін, сонымен қатар мағынасын терең түсініп, ұғуға ықпал
жасайды. Сондай көптеген әдістерді қолдану арқылы экономикалық
тапсырмалардың нәтижесін алуға мүмкіндік беретін Өндірістік және
экономикалық процестерді модельдеу пәнінің біздің, яғни бағдарламашылардың
өмірінде зор маңызы бар. Себебі осы пәндегі көптеген тәсілдерге біз
бағдарлама құру арқылы оның нәтижесін тез ала аламыз.

1. Жалпы бөлім

1 Пәндік аумақтық сипаттау

Модель – кез-келген заттың, мәселенің, процесстің өңдеуге және
басқаруға қолайлы түрдегі формасы.
Модельдеу этаптары:
1 Мақсатты анықтау – бұл модель құру барысында бізге не керек соны
анықтау керек.
2 Параметрлерді анықтау – есептің берілгендері аталады.
3 Басқарушы айнымалыларды анықтау – олардың мәні табылғанда есептің
шешімі шығатын айнымалылар.
4 Шектеулерді анықтау – басқарушы айнамалылардың қабылдайтын мәндерінің
жиыны.
5 Кездейсоқ факторларды анықтау – зерттеушіні еркінен тыс оған
бағынбайтын факторлар.
6 Бірінші бөлімнен анықтаған мақсатты жоғарыда айтып кеткен
параметрлер, басқарушы айнымалылар және кездейсоқ факторлар арқылы
өрнектеу.
Дискретті модельдер – дискретті сигналдарды пайдаланады. Үзіліссіз
модельдер үзіліссіз сигналдарды пайдаланады.
Белгісіз факторлар ескерілмейтін модельдер деп айтылады. Олар:
- сызықтық
- сызықтық емес
- динамикалық
- графикалық
Сызықтық модельдер деп не функцияда және шектеулерде сызықтық
функциялары бар модельдер.
Сызықтық емес деп не функцияда не шектеулерге айнымалының сыықтық
емес түрі араласқан моделі.
Динамикалық модельдерде уақыт ескеріледі.
Стохастикалық модельдерде айнымалылар және параметрлер кездейсоқ
немесе бізге белгісіз заңдылықпен анықталады. Олар математикалық күту,
дисперсия, орта квадраттық ауытқу.
Жалпыға қызмет көрсету модельдері:
- лифт
- эскалатор
- кассалар
Бұл модельдерге шығынды белгілі заңдылықтарға бағынбағанда қолданыс
болып табылады. Ойындар теориясы моделінде есеп ойын түрінде қарастырылады,
онда бірнеше ойыншы болады. Мысалы: конкуренция тұрғысындағы нарық.

- иммитациялық модельдер – нақты объектте модельдеу мүмкін болған
жағдайда қолданылады.
Кез-келген модельді құру кезінде келесі деңгей этаптарын ұстанған жөн.
Негізгі модельдеу этаптары:
1 Берілген жұмысты шығарып, қандай мақсатқа жеткізуді анықтау.
2 Модель параметрлерін анықтау, яғни мәндеріне зерттеу әсер етпейтін,
алдын-ала белгіленген факторларды анықтау.
3 Мәндерін өзгерте отырып басқарушы айнымалыларды қалыптастыру.
Басқарушы айнымалылардың маңызы бұл жұмысты шешу.
4 Басқарушы айнымалыларды шектелген аймақтарда анықтау, берілген
есептерді шығару.
5 Белгісіз факторларды анықтау. Оның көлемінің ойда жоқта өзгеруі
мүмкін немесе анықтаусыз қалпында болады.
6 Жұмыстардың оптималды эффектісі дегеніміз - барлық тұтас қызметінің
құрастырылуы. Басқарушы айнымалысы арқылы мақсаттың өрнектелуі.
Келесі шартты белгілерді енгіземіз:
α – модель параметрі
х – басқарушы айнымалылар немесе есептеулер
Х – аймақтық есептерге рұқсат етуі
β – кенеттен немесе анықталған факторлар
W – тұтас қызметі немесе критерий эффектісі
Тауарды өткізу жұмыс жоспарын құрастыру.
Әр-түрлі фирмада әр-түрлі заттарды өткізеді.Ол үшін арнаулы заттарды
пайдаланады.(техникалық,ақшалай,ада ми)Заттардың жалпы артығы, әр заттардың
санын өткізуде тауардың бірлігін пайдалана отырып өткізу.Сол затты
сатқандағы түскен пайдасы. Заттарды өткізу жоспарын құрастырғанда, соған
сол фирмадан көп пайда түсуіне мүмкіндік жасау.
Нәтижесінде моделдің есебі. Әр заттардың сандық көрcеткіштермен
анықтайды, фирмаларда максимальды пайда түсірумен қамтамассыз ету.
Жабдықты тиімді енгізудің есебі
Кәсіпорын қолда бар жабдық көмегімен өндірістік тапсырманы орындауы
қажет. Жабдықт бірлігінің әрқайсысына берілген:
- жұмыс уақытының қоры
- өнім түрінің әр данасын дайындауға кететін өзіндік құны
- өнімділік, яғни уақыт бірлігімен көрсетілетін өнімнің әр түрінің
данасының саны
Жабдық арасында өнімнің жалпы өзіндік құны аз болатындай етіп,
өнім шығуын тарату керек.

1.2. Математикалық модельді құру

1. Мақсат болып - өзіндік құнды минимизациялау табылады
2. Модель параметрі:
n – жабдық бірлігінің саны
m – номенклатура, яғни өндірістегі өнімнің саны

bi - өнім бірлігінің саны i – түрі, i =1.. m;
aij – i түрінде өнім өндіргендегі j түріндегі жабдық
өнімділігі
Tj – j түріндегі жабдықтың жұмыс уақытының қоры, i =1.. m; j =1..
n;
3. Басқарушы айнымалылар xij, i =1.. m; j =1.. n – бұл j түріндегі
жабдық i түріндегі өнімді өндіру кезіндегі уақыт.
4. ОДР жұмыс уақыты қорының шектелуі және номенклатурасы xij оң емес
Модель m * n белгісіз (басқарушы айнымалылар) кері еместік шартты
есепке алмағанда m+n шектеулері бар. Модельді есептеуден кейін жабдықты
тиімді енгізу анықталады, яғни жабдықтың өнімді дайындауға кететін уақыты.
Материалды пішу
Пішуге (аралауға) материалдардың анықталған түрлерінің бірнеше саны
араласады. Олардан бірнеше өнім жасалуы тиіс. Материал әр-түрлі тәсілдермен
пішілуі мүмкін. Кез-келген тәсілде өзіндік құны бар және әр-түрлі өнім
алуға мүмкіндік береді. Ең минималды жалпы өзіндік құны бар пішу тәсілін
анықтау.
Математикалық модельді құру
1. Пішудің өзіндік құнын минимизациалау мақсат болып табылады.
2. Параметрлер:
n – пішімге түсетін материалдар түрі;
dj - j түріндегі материал саны j = 1.. n;
m - өнімді дайындау үшін қажет материал түрі;
bi – і түріндегі өнім саны,
l – пішудің түрлерінің саны
aijk - j түріндегі материал бірлігінен k түріндегі тәсіл бойынша
алынатын і түріндегі өнім саны, і =1.. m, j =1.. n, k=1..1;
с jk - j түріндегі материалды k түріндегі тәсілмен пішудің өзіндік
құны, j =1.. n, k=1..1;
3. Басқарушы айнымалылар хij - j түріндегі материал бірлігінің саны k
түріндегі тәсіл бойынша анықталады j =1.. n, k=1..1;
4. Рұқсат етілген шешімдер аймағы қолданылатын материалдар саны
шектеулерімен шығару шектеулерімен және басқарушы айнымалылардың кері
еместік шарттарымен анықталады.

12 Модельдерді есептеу әдістері

Сызықтық модельдер деп не функцияда және шектеулерде сызықтық
функциялары бар модельдер.
Сызықтық емес деп не функцияда не шектеулерге айнымалының сыықтық емес
түрі араласқан моделі.
Динамикалық модельдерде уақыт ескеріледі.
Стохастикалық модельдерде айнымалылар және параметрлер кездейсоқ
немесе бізге белгісіз заңдылықпен анықталады. Олар математикалық күту,
дисперсия, орта квадраттық ауытқу.

1. Арнайы бөлім
1. Ойындар теориясының негізгі түсініктері және анықтамалары

Тиімділік есептерінің басты шарттарының бірі - бұл белгісіз жағдайларда
белгілі бір шешім қабылдау. Ойындар теориясы – бұл теория ойыншылардың
қызығушылары әр-түрлі жағдайларда, яғни ойындар теориясында әрбір ойыншы өз
мақсатына әр-түрлі жолдармен жетеді.
Арнайы терминдер:
I. Ойыншылар ойыға қатысып отырған жақтар немесе конфликтіге қатысып
отырған жақтар.
II. Ұтыс. Конфликттің нәтижесі.
III. Жүріс. Белгілі бір ережелерді сақтап, жолдарды қолдану және таңдау.
IV. Стратегия. Ойыншының өз қалауын жасайтын жоспар.
V. Тиімді стратегия. Бұл ойыншыға минималды орташа ұтыс әкеледі немесе
минималды орташа ұтыс әкеледі.
Жағдай конфликтті болып саналады егер бұл жағдайға қатысып отырған
жақтардың қызығушылары қарама-қарсы болса.
Ойын – бұл кем болмағанда екі адам қатысып отырған нағыз немесе
формалды конфликт.
Егер ойыншылардын саны 2-ге тең болса ойын қарапайым болып саналады.
Айталық екі ойыншы болсын:
А ойыншы өзінің m стратегиясына і-нші стратегияны қалайды.
В ойыншы n-ыншы j-інші стратегияны қалайды.
Нәтижесінде А ойыншы аіj шамасын ұтып алады. Ал В ойыншы сол шамадан
ұтылады.

А=

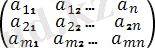
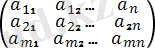
A=(A1, A2...Am)
B=(B1, B2...Bn)

A матрицасы томақы матрица деп аталады.
α саны ойынның төменгі бағасы деп саналады, ал α стратегиясы
максимильдік стратегия деп аталады.

α=max(min aij) (1)

β саны жоғарғы саны деп аталады, ал β стратегиясы минималды стратегия
деп аталады.

β=min(max aij) (2)

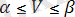
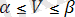(3)

Егер А=β=V болса онда ойын ершік нүктесі деп аталады.
Егер αβ болса аралас стратегия қолданылады.

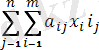
(4)

1 Теорема. Әрбір матрицалық ойын өз шешімін аралас стратегиялар арқылы
есептеледі. Таза стратегия аралас стратегиялардың түрі деп саналады.

2 Теорема. В ойынның бағасы болып, ал х*y* ойынның тиімді стратегиялары
болуы үшін келесі шарттардың болуы қажетті

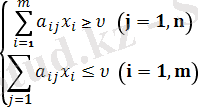
(5)

3 Теорема. Егер ойынның бірі тиімді стратегияны қолданса, онда ойынның
бағасына тең.

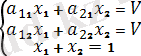
(6)

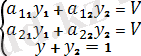
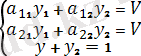(7)

Ойындар теориясының 2 әдісі бар:
1. Аналитикалық
2. географиялық

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.