Эксперттік жүйелердегі анықсыздық: сенімділік коэффициенті, шартты ықтималдық, айқын емес логика және мүмкіндік теориясы


МАЗМҰНЫ
Кіріспе . . . 5
І - бөлім
- Анықсыздық көздері . . . 6
1. 2. Сенімділік коэффиценті . . . 10
1. 3 Сенімділік коэффициенті және шартты ықтималдылық . . . 12
ІІ бөлім
2. 1. Айқын емес көпшілік . . . 16
2. 2. Айқын емес логика . . . 18
2. 3. Мүмкіндік теориясы . . . 20
ІІІ бөлім
3. 1 Анықталмаған мәселелердің анықталмаған жағдайы . . . 22
Қорытынды . . . 23
Қолданылған әдебиеттер . . . 25
КІРІСПЕ
Эксперттік жүйелер (ЭЖ) - бұл жасанды интеллект (ЖИ) облысындағы анық және жылдам үдеуші бағыты. ЭЖ пайда болған кезінен бастап өзіне қызығушылық білдіретіні -адам шығармашылығының кейбір облыстарындағы тапсырмаларды шешу мүмкіндігі болып табылады. Мүмкін ЭЖ қолданылмаған немесе кем деген де ондай әрекет жасамаған проблемалық облысы табылмас.
ЭЖ - өз облысы бойынша қандай да бір мәселені шешкенде эксперттің функцияларын орындайтын программалық қамтама немесе программалар жиынтығы. ЭЖ эксперт-адамындай өз жұмысын орындаған кезінде біліммен байланысады. ЭЖ-дің жұмысына қажет пәндік облысы бойынша білім ЭЕМ жадысында формалданан және жүйенің дамуы кезінде өзгеріп және толықтырылып отыратын білім базасы ретінде ұсынылған.
ЭЖ кеңес береді, талдау жүргізеді, топтастыруды орындайды, диагноз береді және кеңес береді. Олар тапсырмаларды шешуге негізделген және әдетте адам-экпертпен экспертиза өткізуді талап етеді. Процедуралық талдау қолданатын машиналық программаларға қарағанда ЭЖ дедуктивалық пікір негізінде тапсырмаларды тар пәндік облыстарында шешеді. Бұндай жүйелер көбінесе құрылымсыз және шамалы анықталған тапсырмаларды шешуге қабілеті бар. Олар эвристикалық тартуы жолымен құрылым жоқтығымен келіседі, яғни толық талдау жүргізу үшін қажетті білімнің немесе уақыттың жетіспеуі кезіндегі жүйелерге төбеден алынған ережелері.
ЭЖ басты ерекшелігі - білім жинау мүмкіндігі, оларды ұзақ уақыт сақтауы, жаңарту және онымен нақты ұйымның, ондағы квалификацияланған мамандардан тәуелсіздігін қамтамасыз ету. Білімді жиниауымен тексерілеген шешімдердің жақсыларын қолданып, кәсіпорында жұмыс істейтін мамандардың квалификациясын көтеру болып табылады.
Экономикада және көлік құрылыс кәсіпорындарында жасанды интеллект машықтық қолдануы ЭЖ -ге негізделген.
- АНЫҚСЫЗДЫҚ КӨЗДЕРІ
Мәселені шешу кезінде біз әдетте кездесеміз көптеген көздердің белгісіз ақпарат қолданылатынын, бірақ көптеген жағдайда оларды 2 категорияға бөлуге болады. Жетіспейтін толық білім аймақты пәндер және жетіспейтін мәліметтер жақсы жағдайлар болады. Теория пәндер аймағы біздің біліміміз осы аймақ туралы түсініксіз және толық емес болуы мүмкін. Онда жетіспейтін нақты форалданған концепциялық немесе құбылыстарды оқу жетіспеушілігі қолданылады. Мысалы диагностикада психологиялық ауырулар бар бірнеше ерекшеленген шизафренді симптомалардың пайда болуы. Белгісіз білім мынаған соқтырады, не ереже әсері жай жағдайларда әрқашанда мәнді нәтижелер бермейді. Толық емес білімді береді. Біз нақты болжай алмаймыз, қандай эффект береді немесе басқа іс қарайды:Мысалы: Терапияда қолданылатын жаңа препораттар көбінесе күтпеген нәтижелер береді және сонында пәндер аймағы теориясын толық біз білгенмен, эксперт санауы мүмкін, эфектылықты қолданады, эвристикалық әдістер дәл емес. Осындай әдістер дұрыс емес алып тастау керек. Электрондық блокта ауыстыру жолымен күдікті түйіндер өте эффекті болып шығады. Струплезді анализ шынжыры іздеу бөлшектерді қатардан шығарып тастайды. Бірақ дәл емес білімдер белгісіз болуы мүмкін, дәл емес немесе жақсы жағдайлар немесе мәліметтер керексіз болуы мүмкін. Әрбір сенсор шектелген рұқсат етілген мүмкіндіктер және 100 % -дік сенімді емес. Есеп беруді құрғанда, қателер болуы мүмкін, немесе олардың дұрыс емес мәліметтер түсуі мүмкін. Тәжірибеде әрқашан толық жауаптар алу мүмкін емес қойылған сұрақтарға және қосымша әртүрлі ақпараттар қолдануға болады. Мысалы: қымбат процедура мен хирургиялық жолмен көмектеседі мұндай әдістер өте сирек қолданылады. Қымбаттығына және қауіпсіздігіне байланысты. Барлық уақыттың факторы бар. Керек мәліметтерді жылдам алуға мүмкіндік жоқ, қандай жағдайға тез шешім қабылдау керек болады. Егер ядролық реактор жұмыста қауіп тудырса тексерулердің бітуін кім болса да күтпейді, оны тоқтату жөнінде шешім қабылдайды. Айтылғандардың барлығын қосса, ескерілетін жағдай эксперименттер дұрыс емес әдістерді екі негізгі себептерге бөліп қолданады. Дәл әдістері жоқ, дәл әдістері бар, бірақта тәжірибеде қолдануға болмайды, себебі белгілі көлемдегі мәліметтер болмайды және құнына байланысты қатерлі мүмкіндікті, мәліметті жинауға уақыты жоқ. Көптеген зертеулер айналасыда жағдай жансыз интелектерді бір шешімге келген, не дұрыс емес әдістер рол ойнайды. Негізгі рол эксперименттік жүйені құрайды бірақта көптеген таластырар сұрақтар туғызады, қандай әдіс қолдану керек. Ақырғы уақытта көбі бірдей келісті, Мак Карти және Хейеса айтқанындай мүмкіндік теориясы тапсырманы шешуде адекваттылық құрал болмайды. Берілген белгісіз білім және мәліметтер (Me Canthy and hayes ) 1969 жылы шықты.
Мына пікірге келесі аргументер кіреді.
Мүмкіндік теориясы сұрақа жауап бермейді, мүмкіндікті сандық мәліметтен біріктіру қалай болады екенін көрсетеді.
Ықтималдылықтардың тағайындалуы белгісіз ақпаратты талап етеді. Түсініксіз сандық бағалау мұндай жағдай әрқашан кездеседі тәжірибеде, түсініктер көптеген жағдайда сирек және мұндай шамамен бағалау, қандай ескі немесе биік мүмкіндік теориясын қолдану тыйымды. Инженерлерден параметірлердің нақты бағасын беруге талап етеді, және олар дәл бағалай алмайды. Бағаны жаңарту өте қымбат тұрады. Қаншама үлкен көлемді аударуды қажет етеді. Барлық осы ойлар жаңа формалардың ақпаратында жұмыс істеу үшін туады, қайсысы тақ емес, логика деген атау алады немесе сенімділік теориясы деп атайды. Соңғы жылдары адвокаттар мүмкіндік теориясын қолданды.
D шартты ықтималдылық оқиғаның S берілсе- бұл ықтималдылық D оқиғасы келіп түскендегі S оқиғасы болып табылады. Мысалы: Егер науқас шынын да D ықтималдылығына тырысса, онда оның тек S симптомына ие болғанын білдіреді.
Дәстүрлі мүмкіндік теориясы шартты ықтималдылықтар жағдайында D берілсе, ал S келесі формулада қолданылады.
P(d/s) =(d^s) /p(s)
Көріп тұрғандай негізгі мүмкіндік терминдері табылады, ұқсастық мүмкіндігі пайда болу жағдайында D немесе S түрінде және мына формуламен шығарылады.
P(D^S) =P(D/S) P(D) (1)
Егерде екі бөліке бөлсек P(S) және оң жақ бөлігіне қойса, (1) ережесіне байланысты Бейес жалпы түрін аламыз.
P(s/d) =(s/d) P(d) /P(d) . (2)
Бұл ереже, кейдеинверсия деп аталатын функцияның шартты ықтималдылығы үшін оның P(D/S) тең болғанда D оқиғасының анықтамасы рұқсат береді, бірақ D оқиғасының пайда болуы P(S/D) шартты ықтималдылық S оқиғасы арқылы таны алатындығы болып отыр. P(D) априорлы ықтималдылыққа ие болған мәндер P(D/S) апостерорлы ықтималдылық оқиғасына тең, онда D оқиғасы S оқиғасының белгілі болған жағдайда салыстырып орындалғанын қамтамасыз етеді.
Жүйеге арналған білімдерге негізделген формула (1) өте ыңғайлы формула (9. 1) сіздің бұған көзіңіз жетеді. Болжаулар бойынша науқастың ауруының белгісі деп болжайық, мысалы: омырауы ауырады оны білу үшін қандай мүмкіндіктерді білу үшін бұл симптома белгісі ауру белгісі.
Мысалы: Инфарк миокарда және перикарда (өкпенің ауыруы) немесе бұданда қауіпті асқазан қорытпауы сияқты есептеп шығару P(инфарк миокардо кеуде ауруы) формула (1) білу керек. Немесе қанша адамды әлемде мұнай ауырумен аурады. Инфарк пен миокарда және омырау аурулары шағымдар түсіреді. Ереже бойынша мұндай ақпарат жоқ және соңында қайсысы керек екенін анықтап есептеп шығару үшін P сол сияқты табу формаласы мен берілген (1) Клиникалық тәжірибеде қолдана алмайды.
Белгіленген қиындық алынған кейін керек ақпарат көптеген специолистердің теріс қарым-қатынаста себеп болды. Бұл теріс қарама-қарсы нығайтылды, класикалық көптеген жұмыста мүмкіндік теориясының түсінігі табылды. Қанай обьективтілік анығырақтың пайда болуы жалғастырылған тәуелсіз жасалған пікірлері бар. Бұл базалық болжамдар теңестірілусіз тәжірибелік пікірлер көзге түсті. Мысалы [Pearl 1982] және (Cheeseman 1985) жақтаушалары бұл субьектіні ұстанады. Анықтауыш мүмкіндігі кейбір жағдайдың пайда болу ісімен бағаланады, мұндай көзқарас заттарды байланыстырады, мүмкіндік жағдайлары субъективтілікке сенімді жағдайлар анығында түсіріледі.
Мысалы: дәрігер білмеуі мүмкін немесе табуға мүмкіндік жоқ қандай науқас бөлігі омырауының ауыратынын инфаркт ауратынын, бірақ та өзінің тәжірибелеріне сүйене отырып бағалайды, қандай бөлігінде науқастың аурумен ауратындығын. Куәгерлер оның нық мағынасын бағалай алады, P(субъектілік пікір табиғат анық Бейеса ережесімен тығыз байланысты) .
Мына себептерге байланысты, бізде бағалайтын жеткілікті мәліметтер бар делік, 5-синдром мағынасын береді, d-ауру формасы бойынша(2) анықтап есептеуге болады, мағынасын бағалау, дәрігер өзінің зертеулерінде негізіндеуге мүмкін. Есептеулер қиындық туғызбайды, бір симптом жайлы сөз болғанда, көптеген аурулар бар P және көптеген симптом S әрқайсына D есептеу анықтау керек, науқастарға осы аурумен ауратындар тексеріледі.
Бір анықталған симптом мүмкіндіктерінен S көптеген D бар мүшесі көптеген S-n мүшесі есептеуді қажет етеді, mn+m+n бағалау оңай жұмыс, егер медициналық диогностика жүйесі қолданылады. 2000 түрлі ауру және үлкен сан әртүрлі симптомдар бар. Бірақ жағдайлары қиынырақ, егер біз процеске қойылған диогнозге біреу емес бірнеше симптом қосып көрсек.
Бейеса ережесі жалпы мына формула түрінде:
P(d/sl^…^sk) =P(sl^…^sk/d) P(d) /P(sl^…^sk) (3)
және есептеуді қажет етеді (mn) k+m+nk бағалау үлкен емес мағнада да А: Бұл бағалау қажет етеді, сол себептен жалпы жағдайда есептеулер P(sl^…. ^sk) алдын ала есептеу керек, P(s1s2^…^sk) =P(s2s3^…sk) …. P(sk) . біреуін егер болжасақ кейбір симптомдар бір-біріне тәуелсіз көлемі есептеулер төмендейді. Тәуелсіз әрбір пара симптом Si және Sj мағнасы P(Si) =P(Sl\Sj) .
Онда мына қатынас шығады:
P(Si^Sj) =P(Si) P(Sj) .
Егер барлық симптом тәуелсіз көлемін есепте. Симптомда бір диогноз тіркелген болса жағдай қалай болса олда солай болады. Бұл бірақ болмаған жағдайда тәуелсіздікті тікелей болжауы мүмкін. Бұл мағына парасимптом S\ және Sj тәуелсіз болады. Көбіне біздің қарауымызда кейбір қосымша куәліктер бұған байланысты және фундаменталдылық білім Е. Осымен P(Si, SjE) =P(Si\E)
Мысалы: егер менің көлігімде отын болмаса және жарық жұмыс істемейдімен айталам бұл тәуелсіз симптом, себебі менің білімдерімді көліктің бөліктері толық бар, деп болжка үшін олардың арасында себептер байланысы жоқ. Бірақ егер көлігім тұтанбаса және жарық істемесе бұл симптом тәулсіз деп атау дұрыс емес, себебі олар болуы мүмкін, демек сол бір аккумулятор батареясынан болуы мүмкін. Сенімділік деңгейі симптомда жарық жұмыс істейді, егер пайда болса, онда қозғалтқыш іске қосылмайды. Қажеттілік бақлауда програмалардың байланысында және сенімділік деңгейін жобалау симптомы көлемін үлкейтеді, жалпы жағдайда есепптеулер осындай мақсатта қолданылады. Ықтималдылықтар теориясында біздің алдымызға келесі мәселені қояды, барлық таңдалған тапсырма терминдерін біріктіру керек. Немесе априори болжанады, барлық мәліметтер тәуелсіз және қолдану есептеу әдістерін төлеуге тура келеді, нәтижелер дәлдігі төмендейді. Тәуелсіз мәліметтер қолдану олардың арасындағы байланысты бақылау осы тәуелділікті сандық тұрғыдан бағалау нормативтік ақпаратта негізделген жаңартылған шындыққа шығару. Есептеуді қиындату бірақ өте дұрыс нәтижелер берілген. Символдық әдістерін бақылау тәуелсіздік арасына қолданылатын мәліметтерді кейбір сандық әдіс моделінен тәуелсіздік арасындағы ықтималдылықты сипаттайды. Келесі бөлімінде біз қарастырамыз. Кейбір қиындықтарды эксперттік жүйесінде құрылғыларын қарастырамыз.
1. 2. СЕНІМДІЛІК КОЭФФИЦЕНТІ
Біз сенімділік коэффицентіне ораламыз, 3 тарауда айтылып кеткендей MYCIN жүйесіндегі принцеп жұмыстарын қарастырамыз. Идеолдық әлемде ықтималдылықты есептеуге болады P(Di) қайда Di-i-я диогностикалық категориялар, a & қажеті толықтыруларды көрсетеді немесе фундаменталді білім, және ықтималдылықты пайдалану Fi клиникалық бақылауларды меңгереді. Біздер Бейса ережесіне және есептеулерді орындауына сенімді болдық, ол біріншіден барлық мағынаға ие болса P(Si/Di) және екіншіден шындыққа жақын сөздер тәуелсіз симптомада MYCIH жүйесінде қолданылады.
Егер науқасқа көрсетілген симптом болса Sl^…^Sk және оның орны фондық шартта белгіленеді, науқас ауыруына сенімді болса, онда науқас аурумен аурады. Сенімділік коэффиценті T диопозрны [-1+1] мынадай мағнаға ие болады, T=+1 барлық айтылған шарттарды сақтау ережесі құрылады шешілетін шындығына сенімді, Di ал егер T-1 аталған барлық сақтаулар шарттарды сенімділік қателігі осы шешімнен күшті +1 оң мағынаға ие болады. Сенімділік коэффициент сенімділігі көрсетіледі. Шешімнің дұрыстығын Di а теріс мағына дәрежесіне ие болады және сенімділігі оның қателіктерінде көрсетіледі. Негізгі идея мынадан тұрады, ереже көмегімен пайда болған, осы түрдегі өзгертуге және анықтауға тырысады, P(Di) Sl…^sk) келтірілген бағасы сол бейнеде тексеріліп қаралады. 3 тарауда көрсетілгендей ережені қолдану нәтижелері мұндай түрдегі сенімділік коэффициентіне байланысты болады. CT- көмегімен соңғы шешім сенімділік мағынасы а, ал қосымша шарт t1^…^tm ; Тm және фондық білімді ұсынады және нақты ережені қолданумен шектеледі. Көбінесе бұл шарт интерпретативті мағынаны яғни «ақиқат»немесе «өтірік», +1 немесе -1 коэффициентінің мағынасы болуы мүмкін. Сондықтан бірлік коэффицентінің симптомының мінездемесі Sl^…^Sk тең болады. Фондық білім ережеге сай емес анықтамаларға тиым салады. Мысалы диагностикалық ереже бойынша жүктілік болуы мүмкін. Бұл ереже тек әйел адамдарға ғана тән болуы тиіс, себебі ол фондық білім болып табылады.
Бучана және Шортлифф дәлелдегендей, қатаң түрде Байес ережесін жазсақта бұл толық мағынаны бермейді, себебі бұл субьекті ықтималдық болып табылады[Buchanan and Shortliffe, 1984, Chapter 11] . Өзіміз көргендей негізгі аргумент ықтималдылыққа қарсы жақындау. Бірақ мұндай аргумент ықтималдық туралы обьективті түсінікті болжайды. Сонымен қатар «дұрыс» мәндер өмір сүреді, бірақ біз оны қолданыла алмймыз, бұл Байес ережелеріне қарсы. Бұл аргументтің схоластикалық реңкі бар, себебі кез-келген инженерлік білімнен өткен экспертиза адам қолымен істелетін болғандықтан дүние жүзі мойындайды. Теорияның көзқарасы бойынша айқын емес деректерге формализм гөрі матиматикалық формализмді қолданған жөн.
Перл [Pearl, 1988, p. 5] ережесінде негізделген керекті практикалық жақындауға көңіл бөлді. Сенімділік коэффициенттінің қортындысы берілген ережеден басқа бөтен ақпаратты қабылду мүмкін емес болғандықтан, модулдік түрде мінезделеді. Сондықтан шығыс деректерін мінездейтін сенімділік коэффициенттінің мағынасы болмайды.
Эксперттік жүйелерді құрған кезде осы негіз қолданылады. Барлық анықталған параметрлері бар ережелер үшін алғы шарт әр ереже логикалық тәуелсіз болып саналады. MYCIN жүйесін анализ деген Шортлифф көптеген тәуелсіз белгілерді біріктіру үшін жалпы бір ережені ойлап шығаруды ақыл берді.
Мысалы Е 1 және Е 2 белгілерінің арасында тәуелсіздік болса, алдымен Е 1 болса, онда Н с қортындысы сенімді түрде t келеді, ал Е 2 болса, олда да Н с қортындысы сенімді түрде t келеді.
Осы анықтамада ықтималдық теориясының негізі бар. Талап ықтималдығын модулі ретінде қарастыру мүмкін емес. Анықтама:
P(B\A) =t
1. 3 СЕНІМДІЛІК КОЭФФИЦИЕНТТІ ЖӘНЕ ШАРТТЫ ЫҚТИМАЛДЫЛЫҚ
Адаме көрсетті, егер қарапайым ықтималдық моделі Байес ережесіне негізделсе, онда MYCIN жүйесіндегі сенімділік коэффициенттінің гипотезі [Adams, 1976] белгілерін шешу кезінде гипотез ықтималдылығына сәйкес келмейді. Бірақ Адаме сонымен қатар егер сенімділік коэффициентті екі гипотез сәйкес ықтималдылықпен керісінше саналады. Бұл сұраққа тоқталайық.
Эксперттің қорытындысына негізделгендіктен субьектті P(h) белгілейміз h гипотеза ақиқат болғандықтан ықтималдылық мәні. P(Н) мәні h гипотезінің ақиқттылығындағы эксперт сенімділігінің кезеңін көрсетеді. Бұл жағдайды қиындату үшін бұл гипотезге е мәнін қосымша қолданамыз. P(Н) > P(h) .
Эксперт сенімділік кезеңінде гипотез әділдігі өседі, бұл қатынас төмендегідей болады.
МВ (h, e) =[P(h\e) -P(h) ] \[-P(h) ]
Мұндағы МВ- сенім өлшемін білдіреді.
Егер е белгісі h белгісіне сәйкестелінбесе P(h\e) <P(h), онда бұл гипотездің әділеттілігіні сенімділік өлшемінің экспертті өседі. Сенімсіздік өлшемін MD төмендегідей білеміз:
MD (h, e) =[P(h) -P(h\e) ] \P(H) ]
Түрлі қосымша әдістері бар бір гипотездің сенімділік кезеңі анықталуы мүмкін еместігін Адаме көрсетті.
Егер кейбір белгілер нақты аурудың абсолютті диогностикалық индикаторы болса, егер s 1 симтпомды емделушілер dj ауруымен науқасталса, онда басқа белгілер диагнозды өзгерте алмайды. Басқаша айтқанда, екі қос белгі s 1 және s 2 болады, және
P(d i \s j ) =P(d i \S1^S2) =1
P(d i \s 2 ) =P(d l )
Объективті гипотезге Адаме сынды түрде қарады. MYCIN негізіне қойылған моделі бөлек гипотездің сенімділік өлшемінің d 1 ^d 2 гипотезінің сенімділік өлшемінің кішкенесіне сәйкес келуі тиіс, ал сенімсіздік өлшемі- бөлек гипотездің сенімділік гипотезі үлкен бөлуі керек. Мұндағы d 1 ^d 2 белгілері бір-бірінен тәуелсіз. Онда P(d 1 ^d 2 \е ) =0 кез-келген белгіден е және тәуелсіз сенім өлшемі немесе d 1 нмесе d 2 сенімсіздіктері.
Бучанан және Шортлифф гипотезге арналған сенімділік немесе сенімсіздік өлшем комбинациясын сандық бағалау үшін сенімділік өлщемінің коэффициенттін анықтаған. Олар сенімділік және сенімсіздік өлшемінің арасындағы өлшем айырмшылығын көрсетті:
CF(h, e a ^e f ) = MB(h, e f ) - MD(h, e a ),
e f - гипотезді куәландыратын белгі; һ, а e a - гипотезге қарсы белгілер. Бірақ осындай жолмен алынған мәндер һ гипотезінің ықтималдылығы Байес ережелеріне сәйкес келеді:
P(h\e a ^e f ) =[P(e a ^e f h) P(h] \[P(e a ^e f ) ]
Осылайша сенімділік кезеңі анықталған ережемен болғандықтан сенімділік коэффициентті комбинарлық баға болып саналады. Ол негізгісі төмендегідей болады:
Формальді пікірлерді орындау кезінде программалық қадамдарын басқару;
Кеңестік жағдайындағы ізденіс мақсаттын басқару процессі;
Барлық белгілерді өңдегенен кейінгі гипотез жиынтығы;
Бірақ Адаме көрсеткендей, коэффициент сенімділігіне негізделген гипотез қорытындысы ықтималдық әдісіне қарсы болып келеді. Ол оны нақты келесі мысалды келтіреді.
d 1 және d 2 -екі гипотез, ал е- бір гипотездің куәландырады.
Осындай априорлықтар ықтималдылықтар арасында қатынас болсын:
P(d 1 ) > P(d 2 ) және P(d\ \e) > P(d 2 \e) . Басқаша айтқанда субъективті ықтималдылық d 2 қарағанда d\ гипотезіне әділ болып келеді. Қосымша әдіс қабылданғаннан кейін бұл қатынас сақталады.
Адаме көрсетті бұл қатынаскері блуы мүмкін CF(d 1. e) < CF(d 2. e) сенімділік гипотездің расындағы коэффциент
Ықтималдылықтың келесі мәндерін қрастырайық:
P(d 1 ) =0. 86.
P(d 2 ) =0. 2.
P(d 1 e ) =0. 9.
P(d 2 e ) =0. 8.
Онда d 1 арналған жоғарланған сенімділік (0, 9-0, 8) \0, 2=0, 5 болады, ал d 2 арналған жоғарланған сенімділік (0, 8-0, 2) \0, 8=0, 75
P(d 1 e ) ‹ P(d 2 e ) болғандығына қрамастан CF(d 1. e) < CF(d 2. e) тең болды.
Адаме сенімділік коэффициенттінің «ойластырылмаған қасиеттін» қарастырды. Бұл жағдай болмауы үшін, барлық априорлық ықтималдылық тең болуы тиіс. Жоғарда келтірілген мысалдан шығатын қорытынды е белгісі d 2 қарағанда үлкен априорлық ықтималдылық үшін d 1 куәландырады.
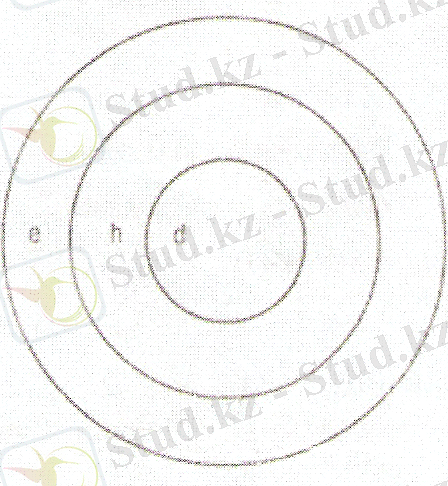
Осылайша транзистік қатынастарда жүйелік ережелерін шығару бірінші қадамда әділ болады, бірақ көп жағдайда олай болмайды деген пікір қалады. Бұл категорияларға байланысты ережелер арасындағы байланыс көбеюі төмендегі 1. 1. суреттегідей болуы мүмкін.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz