Екі еселі, үш еселі, беттік және қисық сызықты интегралдар: теориясы, есептеу әдістері және физикадағы қолданылуы


Мазмұны:
- Кіріспе
- Негізгі бөлімТікбұрышты координаталармен берілген екі еселі интегралҮш еселі интегралҚисық сызықты интегралдарЕкі еселі және үш еселі интегралдардың физикада және техникада қолданылуыҚисық сызықты интегралдарды пайдаланып физикада қолданылуы
- Қорытынды
- Пайдаланылған әдебиеттер
К і р і с п е
Президенті Н. Ә. Назарбаев 2008 жылдың 6 ақпанында Парламент палаталарының отырысында «Қазақстан халқының әл-ауқатын арттыру - мемлекеттік саясаттың басты мақсаты» жолдауында “Білім беру саласының басты міндеті - 2010 жылға дейінгі білім беруді дамыту жөніндегі мемлекеттік бағдарламаны орындай отырып, осы саланың сапалы қызмет көрсету аясын кеңейту.
Бірінші. Білім және ғылым министрлігі үш жылдың ішінде заманға сай білім алуға және озық технологияларды игеруге мүмкіндік беретін білім берудің тиімді инфрақұрылымын жасауды аяқтайтын болсын.
Екінші. Үкіметке, мемлекеттік холдингтерге облыстардың, Астана жіне Алматы қалаларының әкімдерімен бірлесе отырып, кәсіптік-техникалық білім беруді одан әрі дамыту бағдарламасын әзірлеп, іске асруды тапсырамын ” - деп, атап көрсетті.
Осы тұрғыда болашақ математика пәнінің мұғалімдерін даярлау үшін математикалық анализдің физика, экономика, топография, механика және т. б. салаларда қолданбалылығын пайдалану іргелі білімді меңгеруге кең көлемде мүмкіндік туғызады. Математикалық анализ курсындағы беттік интегралдар бөлімінің практикалық мазмұнды есептерді шешуде қолданылуын көрсету арқылы бұл тарауларды меңгеруде жақсы нәтижедерге жетуге болады.
Нақты мысалдарға тоқталайық:
1-мысал.
z = (1/2) (x 2 +y 2 ), (0≤z≤1) формуласымен берілген, тығыздығы μ = z заңы бойынша өзгеретін параболалық қаптаманың массасын табу керек.
Шешуі:
М = ∫ s ∫ μ(x, y, z) dS, (1)
Формуланы пайдаланып, мынаны аламыз:
М = ∫ s ∫ zdS.
S бетінде z = 1/2*(x 2 +y 2 ) теңдігі орындалады. Және Oxy жазықтығындағы радиусы √2 ге тең шеңберге проекцияланып, беттің көптеген нүктелері бойынша интегралданады.
dS = √Ҝ(1+x 2 +y 2 ) dxdy,
осы формуланы және жоғарыдағыны ескере отырып, беттік интегралды 2-ші ретті интегралмен алмастырып, полярлық координаттарға көшеміз:
2π √2 √2
М = (1/2) ∫dφ∫ρ 3 (√1+ρ 2 ) dρ = π∫ ρ 3 (√1+ρ 2 ) dρ.
0 0 0
1+ρ 2 = t 2 деп алмастыру енгізе отырып, мынаны аламыз:
√3 √3
М = π∫t 2 (t 2 -1) dt = π(t 5 /5-t 3 /3) = 9π(6√3+1) /15.
1 1
2-мысал.
Тығыздығы М(х, у, z) әр бір нүкте тығыздығы z/a тең. х 2 +у 2 +z 2 =a 2 (z≥0) формуласымен берілген жарты сфераның массасын анықтау керек.
Шешуі:
(1) формула бойынша
М = (1/а) ∫∫zds,
S
мұндағы, S- берілген жарты сфера.
Жарты сферада мынадай теңдеулер орындалады:
z=√a 2 -x 2 -y 2 , ds=adxdy/(√a 2 -x 2 -y 2 ),
және ол Oxy жазықтығындағы x 2 +y 2 ≤a 2 шеңберіне проекцияланады.
Осыған байланысты, беттік интегралды 2 реттіге алып келіп, алатынымыз:
М = ∫ ∫ dxdy = πa 2 .
x 2 +y 2 ≤a 2
3-мысал.
Координаттық жазықтығына қатысты х+у+z=a, (x≥0, y≥0, z≥0) бірқалыпты үшбұрышты пластинканың статикалық моментін табу керек.
Шешуі:
Ауданы dS болатын пластинка элементінін Oxy жазықтығына байланысты осы элементтің жуықтап статикалық моментін табайық.
Пластинка элементінің осы жазықтықтан ара қашықтығы, dS=√3 dxdy болғандықтан
dM Oxy = zdS = (a-x-y) dS = (a-x-y) √3 dxdy болады.
Пластинканың барлық элементтерін қосу арқылы мына формулаға келеміз:
M Oxy =∫ ∫(a-x-y) dS=√3 ∫ ∫ (a-x-y) dxdy,
S D
Мұндағы, D={0≤x≤a, 0≤y≤a-x}- Oxy жазықтығына түсірілген пластинканың проекциясы. Екінші ретті интегралды шеше отырып, мынаны аламыз:
a a-x a
M Oxy = √3 ∫ dx ∫ (a-x-y) dy = (√3/2) ∫ (a-x) 2 dx=a 3 /2√3.
0 0 0
Симметрияның ұғымы бойынша, мына теңдіктер орынды болады:
M Oyz = M Oxz = M Oxy =a 3 /2√3.
4-мысал.
Oz осіне қатысты тығыздығы ө o -ге, x 2 +y 2 +z 2 =a 2 , (z ≥ 0) формуласымен берілген сфераның сыртқы қабатының инерциялық моментін анықтау керек.
Шешуі:
I z = ∫ ∫ (x 2 +y 2 ) ө(x, y, z) dS, (2) формула бойынша
S
I z =ө o ∫ ∫ (x 2 +y 2 ) dS,
S
мұндағы, I z - Oz осіне қатысты S бетінің инерциялық моменті, S-жарты сфера x 2 +y 2 +z 2 =a 2 (z≥0) .
dS=adxdy/√(a 2 -x 2 -y 2 ),
теңдігіне сүйене отырып, беттік интегралды екінші реттіге айналдыра отырып, мынаны аламыз:
I z =ө o a ∫ ∫ (x 2 +y 2 ) dxdy /√(a 2 -x 2 -y 2 ) .
x 2 +y 2 ≤a 2
полярлық координатарға өте отырып, табатынымыз,
2π a 0 a
I z == ө o a ∫dφ∫ ρ 3 dρ/√(a 2 -ρ 2 ) = 2πө o a(ρ 2 √(a 2 -ρ 2 ) +2∫ρ√(a 2 -ρ 2 ) dρ) =
0 0 a 0
a
(4/3) πө o a (a 2 -ρ 2 ) 3/2 = 4 πө o a 4 /3.
0
5-мысал
(x 2 /a 2 ) +(y 2 /a 2 ) -(z 2 /b 2 ) = 0 (0 ≤ z ≤ b) формуласымен берілген, тығыздығы - ө o -ге тең . x/1= y/0=z-b/0 түзуіне қатысты конусты дененің сыртқы қабатының инерция моментін есептеу қажет.
Шешуі:
Берілген түзу Ox осіне параллель, Oxy жазықтығында жатады және Oz осінен ұзындығы b-ға тең кесіндіні қияды. M(x, y, z) нүктесі конустық сыртқы қабатының бетінің элементіне тиісті және ауданы dS -ке тең. Онда М нүктесінен берілген түзуге дейінгі арақашықтықтың квадраты мына формула бойынша анықталады:
r 2 = x 2 + y 2 + (b-z) 2
ал берілген түзуге қатысты алынған элементтін инерциялық моменті жуықтап мына шамаға тең:
ө o r 2 dS.
Ізделінді инерция моментін I деп алып, мына формулаға келеміз:
I =ө o ∫ ∫ (x 2 +y 2 +(b-z) 2 ) dS.
S
z = (b/a) √x 2 +y 2 , dS=(√a 2 +b 2 ) dxdy/a, осыны ескере отырып және беттік интегралды екінші реттіге алып келсек, мынаны аламыз:
I = ө o √(a 2 +b 2 ) /a ∫ ∫ (x 2 +y 2 +b 2 ((1-(√x 2 +y 2 /a) ) 2 ) dxdy.
x 2 +y 2 ≤a 2
полярлық координаттарға өте отырып, соңынан табатынымыз:
2π a
I =ө o √a+b/a ∫ dφ∫ (ρ 2 +b 2 (1-ρ/a) 2 ) ρdρ =
- 0
а
(2πµ o √a 2 +b 2 ) /a ∫(ρ 3 (1+(b 2 /a 2 ) ) +b 2 ρ-(2b 2 ρ 2 /a) ) dρ =
0
=((2πө o √a 2 +b 2 ) /a) (a 4 /4(1+(b 2 /a 2 ) ) +(a 2 b 2 /2) -(2a 2 b 2 /3) ) =
(πө o /6) (a√a 2 +b 2 ) (3a 2 +b 2 ) .
- Тікбұрышты координаталармен берілген
екі еселі интеграл
Айталық,
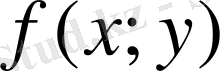 функциясы хОу жазықтығының D шенелген тұйық облысында анықталсын. D облысын аудандары
функциясы хОу жазықтығының D шенелген тұйық облысында анықталсын. D облысын аудандары
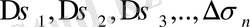 және диаметрлері d
1
, d
2
, . . . , d
n
(облыстың диаметрі деп осы облыстың шекарасының ең қашық екі нүктесінің арасының ұзындығын айтады) болатын “n” облыстарға бөлшектейік. Әрбір элементар облыста кез келген . . . нүктемін таңдап алайық және функцияның . . . нүктесіндегі мәнін осы облыстың ауданына көбейтейік.
және диаметрлері d
1
, d
2
, . . . , d
n
(облыстың диаметрі деп осы облыстың шекарасының ең қашық екі нүктесінің арасының ұзындығын айтады) болатын “n” облыстарға бөлшектейік. Әрбір элементар облыста кез келген . . . нүктемін таңдап алайық және функцияның . . . нүктесіндегі мәнін осы облыстың ауданына көбейтейік.
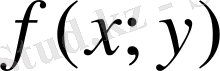 функциясы үшін D облысы бойынша интегралдық қосындысы деп келесі қосындыны айтады:
функциясы үшін D облысы бойынша интегралдық қосындысы деп келесі қосындыны айтады:
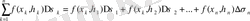 (1)
(1)
Егер maxd k →0 ұмтылғанда интегралдық қосындының D облысын элементар бөлшектерге бөлуге әдісінен және осы облыста Р к нүктелерін таңдап алудан тәуелсіз анықталған ақырлы шегі болса, яғни
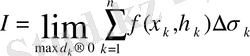 (2)
(2)
онда бұл шек D облысындағы
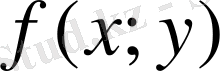 функциясының
екі еселі интегралы
деп аталады және былай белгіленеді:
функциясының
екі еселі интегралы
деп аталады және былай белгіленеді:
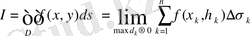 (3)
(3)
Ескерту.
Егер D облысында
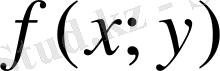 >0 болса, онда
>0 болса, онда
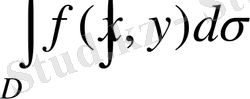 екі еселі интеграл - жоғарыдан
екі еселі интеграл - жоғарыдан
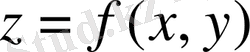 бетімен, бүйірінен құраушылары Oz осімен параллель болатын цилиндрлік бетпен және төменнен хОу жазықтығының D облысымен шектелген цилиндрлік дененің көлеміне тең болады.
бетімен, бүйірінен құраушылары Oz осімен параллель болатын цилиндрлік бетпен және төменнен хОу жазықтығының D облысымен шектелген цилиндрлік дененің көлеміне тең болады.
Екі еселі интегралдың негізгі қасиеттері
1
0
.
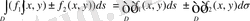
2
0
.
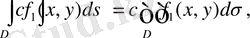 мұнда с-тұрақты сан.
мұнда с-тұрақты сан.
3 0 . Егер D интегралдау облысы D 1 және D 2 облыстарына бөлінсе, онда
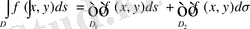
4
0
.
Екі еселі интегралды бағалау.
Егер
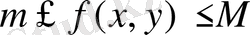 болса, онда
болса, онда
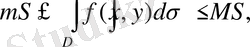 мұнда S - D облысының ауданы, ал m және M -
мұнда S - D облысының ауданы, ал m және M -
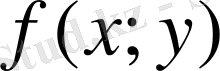 функциясының D облысындағы сәйкес ең кіші және ең үлкен мәндері.
функциясының D облысындағы сәйкес ең кіші және ең үлкен мәндері.
Екі еселі интегралдарды есептеу ережелері
Интегралдау облысының негізгі екі түрі болады.
1. D интегралдау облысы сол жақтан және оң жақтан x=a x=b (a<b) түзулерімен, ал төменнен және жоғарыдан әрқайсысы вертикаль түзумен тек бір нүктеде қиылысатын
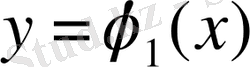 және
және
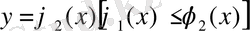 үзіліссіз қисықтармен шектелген (1-сурет) .
үзіліссіз қисықтармен шектелген (1-сурет) .
Мұндай облыс үшін екі еселі интеграл келесі формула бойынша есептеледі:
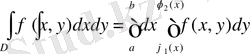
және де алдымен ішкі интеграл
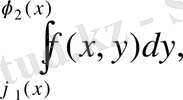 х-ті тұрақты алып есептеледі.
х-ті тұрақты алып есептеледі.
2. D интегралдау облысы төменнен және жоғарыдан у=с және y=d(c<d) түзулерімен, ал сол жақтан және оң жақтан әрқайсысы горизонталь түзумен тек бір нүктеде қиылысатын үзіліссіз
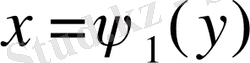 және
және
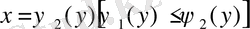 қисықтармен шектелген (2-сурет) .
қисықтармен шектелген (2-сурет) .
Мұндай облыс үшін екі еселі интеграл келесі формула бойынша есептеледі:
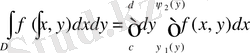
және де алдымен ішкі интеграл
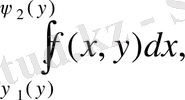 у-ті тұрақты деп алып есептеледі.
у-ті тұрақты деп алып есептеледі.
Көрсетілген формулалардың оң жақтары қайталанбалы интегралдар деп аталады. Жалпы жағдайда интегралдау облысы бөлшектеу жолымен жоғарыдағы негізгі интегралдарға келтіріледі.
Мысалдар:
1.
D облысы
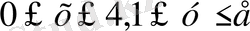 тікбұрышы болғанда
тікбұрышы болғанда
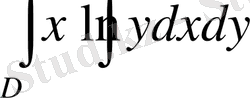 екі еселі интегралды есептеңіз.
екі еселі интегралды есептеңіз.
Шешуі:
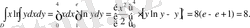
2. D облысы
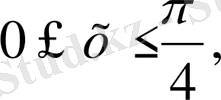
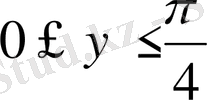 квадраты болғанда
квадраты болғанда

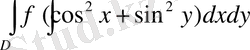 екі еселі интегралды есептеңіз.
екі еселі интегралды есептеңіз.
Шешуі:
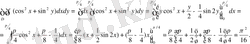
2. 2 Үш еселі интеграл
Айдалық,
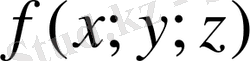 функциясы шектелген тұйық кеңістік Т облысында анықталған болсын. Т облысын кез келген әдіспен диаметрлері
функциясы шектелген тұйық кеңістік Т облысында анықталған болсын. Т облысын кез келген әдіспен диаметрлері
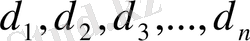 және көлемдері
және көлемдері
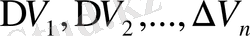 болатын
болатын
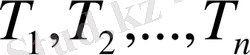 - n элементар облыстарға бөлшектейік. Әрбір элементар облыста кез келген
- n элементар облыстарға бөлшектейік. Әрбір элементар облыста кез келген
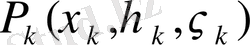 нүктесін таңдап алайық және функцияның
нүктесін таңдап алайық және функцияның
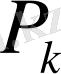 нүктесіндегі мәнін осы облыстың көлеміне көбейтейік.
нүктесіндегі мәнін осы облыстың көлеміне көбейтейік.
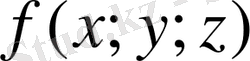 функциясы үшін Т облысы бойынша
интегралдық қосындысы
деп келесі түрдегі қосындыны айтады:
функциясы үшін Т облысы бойынша
интегралдық қосындысы
деп келесі түрдегі қосындыны айтады:
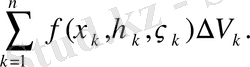
Интегралдық қосындының
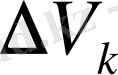 элементар облыстарының диаметрлерінің ең үлкені нөлге ұмтылған кездегі шегін
элементар облыстарының диаметрлерінің ең үлкені нөлге ұмтылған кездегі шегін
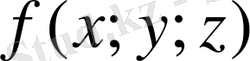 функциясынан Т облысы бойынша алынған үш еселі интегралы деп атайды және ол келесі түрде белгіленеді:
функциясынан Т облысы бойынша алынған үш еселі интегралы деп атайды және ол келесі түрде белгіленеді:

Бұл түрдегі ақырлы шек тек қана шектелген функция үін ғана бар болады.
Егер Т облысында
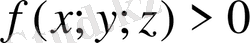 болса, онда
болса, онда
 үш еселі интегралы Т облысын алып жататын және
үш еселі интегралы Т облысын алып жататын және
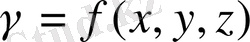 тығыздығы айнымалы болатын дененің массасы болады (үш еселі интегралдың физикалық мағынасы) .
тығыздығы айнымалы болатын дененің массасы болады (үш еселі интегралдың физикалық мағынасы) .
Үш еселі интегралдың негізгі қасиеттері екі еселі интегралдың қасиеттеріне сәйкес болады.
Декарттық координаталарда үш еселі интеграл келесі түрде болады:
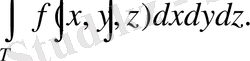
Айталық, Т интегралдау облысы
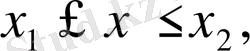
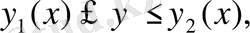
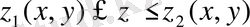 (мұнда
(мұнда
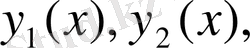
 - үзіліссіз функциялар) теңсіздіктерімен анықталсын.
- үзіліссіз функциялар) теңсіздіктерімен анықталсын.
Сонда
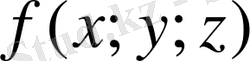 функциясынан Т облысы бойынша алынған үш еселі интеграл келесі формуланың көмегімен есептеледі:
функциясынан Т облысы бойынша алынған үш еселі интеграл келесі формуланың көмегімен есептеледі:
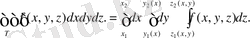
Егер үш еселі интегралды есептегенде x, y, z айнымалыларынан
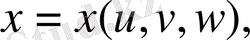
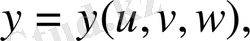
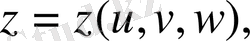 өрнектері арқылы байланысатын
өрнектері арқылы байланысатын
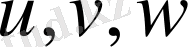 айнымалыларына көшу керек болса (мұнда
айнымалыларына көшу керек болса (мұнда
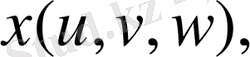
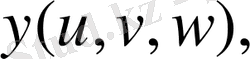
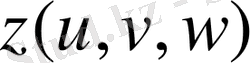 - өздерінің бірінші ретті дербес туындыларымен бірге үзіліссіз функциялар), Oxyz кеңістігінің Т облысы мен
- өздерінің бірінші ретті дербес туындыларымен бірге үзіліссіз функциялар), Oxyz кеңістігінің Т облысы мен
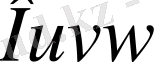 кеңістігінің Т
'
облысының нүктелерінің арасында өзара бірмәнді және екі жаққа да үзіліссіз сәйкестік орнатылады және Т
'
облысында J якобианы нөлге айналмайды:
кеңістігінің Т
'
облысының нүктелерінің арасында өзара бірмәнді және екі жаққа да үзіліссіз сәйкестік орнатылады және Т
'
облысында J якобианы нөлге айналмайды:
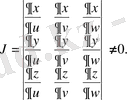
Онда келесі формуланы пайдалану керек:
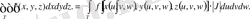
Дербес жағдайда x, y, z декарттық координаталардан осы координаталармен
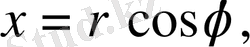
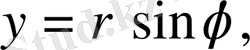
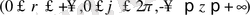 өрнектері арқылы байланысатын
өрнектері арқылы байланысатын
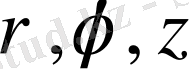 цилиндрлік координаталарға көшу кезінде түрлендіру якобианы
цилиндрлік координаталарға көшу кезінде түрлендіру якобианы
 және үш еселі интегралды цилиндрлік координаталарға түрлендіру формуласы келесі түрде болады (17-сурет) :
және үш еселі интегралды цилиндрлік координаталарға түрлендіру формуласы келесі түрде болады (17-сурет) :
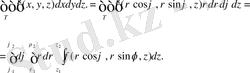
x, y, z декарттық координаталардан осы координаталармен
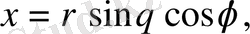
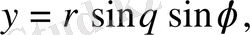
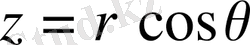 (
(
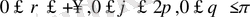 ) өрнектері арқылы байланысатын
) өрнектері арқылы байланысатын
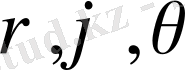 сфералық координаталарға көшу кезінде түрлендіру якобияны
сфералық координаталарға көшу кезінде түрлендіру якобияны
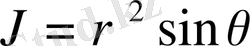 және үш еселі интегралды сфералық координаталарға түрлендіру формуласы келесі түрде болады (18-сурет) :
және үш еселі интегралды сфералық координаталарға түрлендіру формуласы келесі түрде болады (18-сурет) :
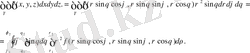
Мысалдар.
№ 1.
Т облысы
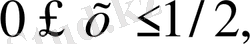
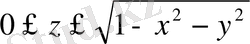 теңсіздіктерімен анықталатын
теңсіздіктерімен анықталатын
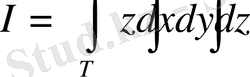 үш еселі интегралды есептеңіз.
үш еселі интегралды есептеңіз.
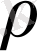
Шешуі:

- Қисық сызықты интегралдар
1. Доғаның ұзындығы бойынша қисық сызықты интеграл.
Айталық,
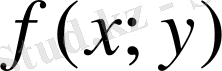 функциясы К жатық қисығының АВ доғасының нүктелерінде анықталған және үзіліссіз болсын.
функциясы К жатық қисығының АВ доғасының нүктелерінде анықталған және үзіліссіз болсын.
АВ доғасын кез келген әдіспен A=A
0
, A
1
, . . . , A
n
= B нүктелерімен n элементар доғаларға бөлейік. Әрбір элементар доғада кез келген
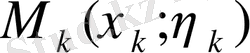 нүктесін таңдап аламыз және
нүктесін таңдап аламыз және
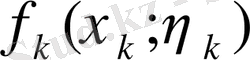 функциясының осы нүктедегі мәнін сәйкес доғаның
функциясының осы нүктедегі мәнін сәйкес доғаның
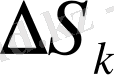 ұзындығына көбейтеміз.
ұзындығына көбейтеміз.
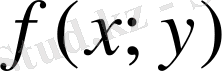 функциясы үшін АВ доғасының ұзындығы бойынша интегралдық қосындысы деп келесі түрдегі қосындыны айтады:
функциясы үшін АВ доғасының ұзындығы бойынша интегралдық қосындысы деп келесі түрдегі қосындыны айтады:
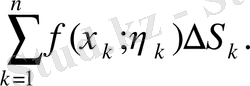
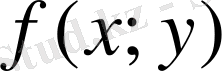 функциясының АВ доғасының ұзындығы бойынша қисық сызықты интегралы (немесе І текті қисық сызықты интегралы) деп
функциясының АВ доғасының ұзындығы бойынша қисық сызықты интегралы (немесе І текті қисық сызықты интегралы) деп
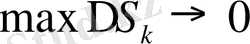 ұмтылған кездегі интегралдық қосындының шегін айтады:
ұмтылған кездегі интегралдық қосындының шегін айтады:

(
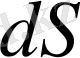 -доғаның дифференциалы) .
-доғаның дифференциалы) .
Егер қисық
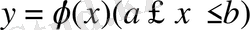 теңдеуімен берілсе, онда І текті қисық сызықты интеграл келесі формулалар бойынша есептеледі:
теңдеуімен берілсе, онда І текті қисық сызықты интеграл келесі формулалар бойынша есептеледі:
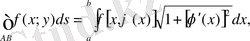
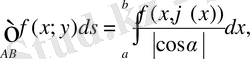
мұнда
 - қисыққа жүргізілген жанама мен Ох осінің арасындағы бұрыш.
- қисыққа жүргізілген жанама мен Ох осінің арасындағы бұрыш.
Егер К қисығы
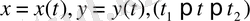 параметрлік теңдеулерімен берілсе, онда
параметрлік теңдеулерімен берілсе, онда
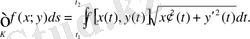
Дәл осылай кеңістік қисық бойынша
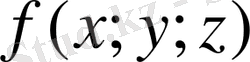 үш айнымалы функциясы үшін І текті қисық сызықты интеграл анықталып, есептеледі. Егер кеңістік қисық
үш айнымалы функциясы үшін І текті қисық сызықты интеграл анықталып, есептеледі. Егер кеңістік қисық
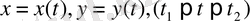 теңдеулерімен берілсе, онда
теңдеулерімен берілсе, онда
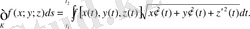
Егер
 болса, онда
болса, онда
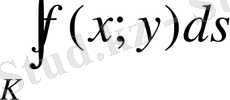 І текті қисық сызықты интегралы
І текті қисық сызықты интегралы
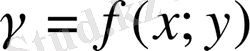 айнымалы сызықтық тығыздығы бар К қисығының массасын көрсетеді (физикалық мағынасы) .
айнымалы сызықтық тығыздығы бар К қисығының массасын көрсетеді (физикалық мағынасы) .
Егер
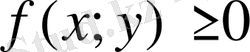 болса, онда
болса, онда
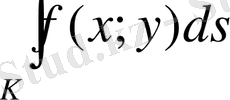 І текті қисық сызықты интегралы К бағыттауышы хОу жазықтығында жататын, ал құраушылары оған перпендикуляр болатын цилиндрлік беттің бөлігінің ауданына тең болады; бұл цилиндрлік бет жоғарыдан
І текті қисық сызықты интегралы К бағыттауышы хОу жазықтығында жататын, ал құраушылары оған перпендикуляр болатын цилиндрлік беттің бөлігінің ауданына тең болады; бұл цилиндрлік бет жоғарыдан
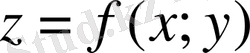 бетімен, ал төменнен хОу жазықтығымен шектеледі (геометриялық мағынасы) .
бетімен, ал төменнен хОу жазықтығымен шектеледі (геометриялық мағынасы) .
І текті қисық сызықты интегралдың негізгі қасиеттері:
1 0 . І текті қисық сызықты интеграл интегралдау жолының бағытына тәуелді болмайды.
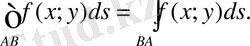
2
0
.
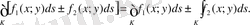
3
0
.
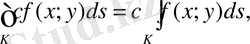 где c = const.
где c = const.
4 0 . Егер интегралдау контуры К 1 және К 2 екі бөлікке бөлінген болса, онда
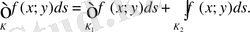
2. 4 Екі еселі және үш еселі интегралдардың физикада және техникада қолданылуы
Егер тығыздық
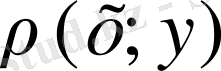 нүктенің функциясы болса, жазық облыстың массасы:
нүктенің функциясы болса, жазық облыстың массасы:
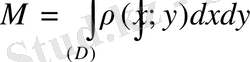
формуласы бойынша есептеледі.
Жазық облыстың координаталық осьтерге сай статикалық моменттері
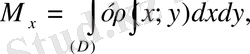
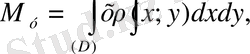
Формулалары бойынша табылады.
Жазық (D) облысының координаталық осьтерге сай инерциялық
моменті:
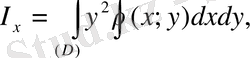
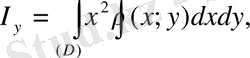
формулалары бойынша табылады.
Координаталар басы О(0; 0) -ға сай инерциялық моменті:
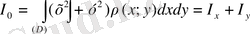 -ке тең
-ке тең
Кейбір түзуге симметриялы орналасқан жазық облыстың центрін іздегенде бұл фигураның ауырлық центрі дәл сол түзудің бойында жататындығын есте сақтау керек. Егер әдейі ескетрпе жасалмаса, алдағы уақытта тығыздықты тұрақты және 1-ге тең деп санаймыз.
4. Жабық
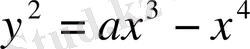 қисығымен шенелген (шекетлген) жазық фигураның ауырлық центрін табу керек.
қисығымен шенелген (шекетлген) жазық фигураның ауырлық центрін табу керек.
Шешуі: берілген қисықты салу үшін берілген функцияны зерттейміз. Айнымалы у теңдеуде жұп дәрежелі, сондықтан берілген қисық Ох осіне симметриялы орналасқан, демек берілген қисықпен шенелген (шектелген) ауданның ауырлық центрі
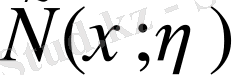 Ох осінде жатады, ал олай болу
Ох осінде жатады, ал олай болу
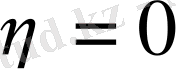 деген сөз. Сөйтіп, берілген қисық - тұзақ болып шықты.
деген сөз. Сөйтіп, берілген қисық - тұзақ болып шықты.
Берілген қисықтың координаталар осьтерімен қиылысу нүктелерін табамыз.
Ох осімен:
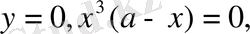


Оу осімен:


Енді берілген қисықтың мінезін туындының жәрдемімен зерттейміз:
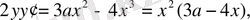
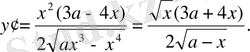
Бұл туындыдан х=0 болғанда
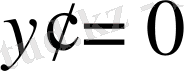 екенін көреміз, демек, қисыққа бұл нүктеде жүргізілген жанама Ох осі болып табылады;
екенін көреміз, демек, қисыққа бұл нүктеде жүргізілген жанама Ох осі болып табылады;
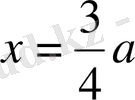 нүктесінде де туынды нөлге тең, сонымен бірге бұл нүктеден өтерде туындының таңбасы плюстен минуске ауысады, демек,
нүктесінде де туынды нөлге тең, сонымен бірге бұл нүктеден өтерде туындының таңбасы плюстен минуске ауысады, демек,
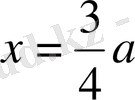 нүктесінде функцияның максимумы бар. Оның шамасы:
нүктесінде функцияның максимумы бар. Оның шамасы:
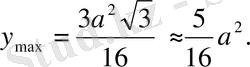
х = а болғанда
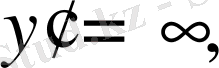 демек қисықтың х = а нүктесіндегі жанамасы Ох осімен бұрыш жасайды.
демек қисықтың х = а нүктесіндегі жанамасы Ох осімен бұрыш жасайды.
Табылған нәтижелер қисықты салуға жеткілікті. (42-сурет) .
әуелі берілген жазық фигураның ауданы S-ты табамыз:

Берілген ауданның ауырлық центрі былай табылады:

Сөйтіп, берілген ауданның ауырлық центрі
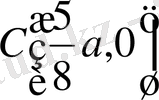 нүктесінде.
нүктесінде.
5.
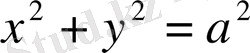 дөңгелегі жартысының диаметрге сай инерциялық моментін табу керек.
дөңгелегі жартысының диаметрге сай инерциялық моментін табу керек.
Шешуі: есеп берілген жарты дөңгелектің Ох осіне сай инерциялық моментін табу жөніндегі есепке айналды. Ол момент
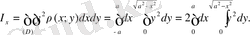
Мұнда жұп функцияның интегралының қасиеті пайдаланылды. Екі еселі интегралды есептеу үшін полярлық координаталары
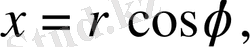
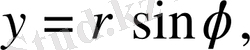
 -ны пайдаланамыз. Жарты дөңгелектің полярлық теңдеуі
-ны пайдаланамыз. Жарты дөңгелектің полярлық теңдеуі
 болады.
болады.
Екі еселі интеграл астында айнымалыларды ауыстырғанда

болады.
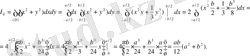
6.
Қабырғалары a мен b-ге тең тік төртбұрыштың өз диагональдарының қиылысу нүктесіне сай инерциялық моментін табу керек (жазық фигура бір текті, яғни тығыздық
 ) .
) .
Шешуі: тік төртбұрышты 44-суретте көрсетілгендей етіп орналастырамыз. Сонда берілген есеп біртекті жазық фигураның координаталар басына сай инерциялық моментін табуға айналады. Сонымен:
7.
Айналу параболоиды
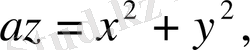 цилиндр
цилиндр
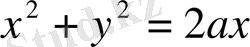 және
және
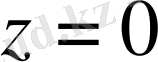 жазықтығының арасында орналасқан дененің көлемін табу керек.
жазықтығының арасында орналасқан дененің көлемін табу керек.
Шешуі: көлемін табу талап етіліп отырған дене 47-суретте кескінделген. Бұл дененің
 жазықтығындағы проекциясы
жазықтығындағы проекциясы
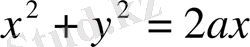 дөңгелегі болады (48-суретте кескінделген) .
дөңгелегі болады (48-суретте кескінделген) .
Берілген дененің
 жазықтығына симметриялылығын пайдаланып, көлемнің жартысын ғана іздейміз. Дененің көлемі үш еселі интегралдың жәрдемімен формуласы бойынша есептелетіні белгілі:
жазықтығына симметриялылығын пайдаланып, көлемнің жартысын ғана іздейміз. Дененің көлемі үш еселі интегралдың жәрдемімен формуласы бойынша есептелетіні белгілі:
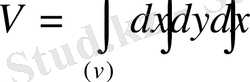
Айнымалы х-тің 0≤х≤2а кесіндісіндегі мәнін бекітсек, х-тің бекітілген кез келген мәнінде у-тің мәні 0-ден
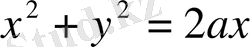 шеңберінің нүктесінің ординатасына дейін, яғни
шеңберінің нүктесінің ординатасына дейін, яғни
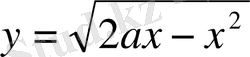 мәніне дейін өзгеретіні көреміз.
мәніне дейін өзгеретіні көреміз.
Бекітілген х пен у те нүкте тек вертикаль бойынша ғана
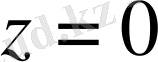 жазықтығынан
жазықтығынан
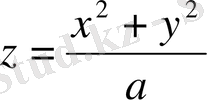 айналу параболоидына дейін қозғала алады.
айналу параболоидына дейін қозғала алады.
Үш еселі интегралды қайталама интегралдармен ауыстырсақ, берілген дененің ізделістегі көлемі былай өрнектеледі:
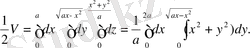
Шыққан интегралды поляралық
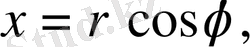
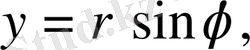
 координаталарына көшіп есептейміз. Сонда облыс шенінің (шекарасының) поляаралық теңдеуі
координаталарына көшіп есептейміз. Сонда облыс шенінің (шекарасының) поляаралық теңдеуі
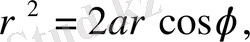
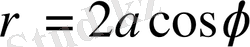
болады.
интеграл астындағы функция
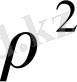 болады, поляаралық бұрыш (жарты көлемге сәйкес) 0-ден
болады, поляаралық бұрыш (жарты көлемге сәйкес) 0-ден
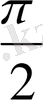 -ге дейін өзгереді. Интеграл астында айнымалыларды ауыстырсақ,
-ге дейін өзгереді. Интеграл астында айнымалыларды ауыстырсақ,
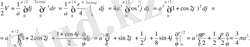
(куб. бірлік) болады.
Ендеше, барлық көлем мұнан екі есе үлкен, яғни
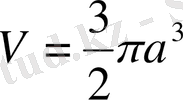 (куб. бірлік) .
(куб. бірлік) .
Егер (V) денесінің тығыздығы
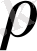 облыс нүктесінің функциясы, яғни
облыс нүктесінің функциясы, яғни
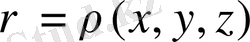 болса, дененің массасы
болса, дененің массасы
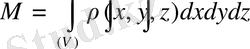
формуласымен анықталады.
8.
Kоординаталық жазықтықтар және x+y+z=1 жазықтығымен шенелген (шектелген) пирамиданың әр нүктесіндегі тығыздығы сол нүктенің координаталарының қосындысына тең, яғни
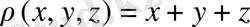 болатын жағдайдағы пирамида массасын есептеп табу керек.
болатын жағдайдағы пирамида массасын есептеп табу керек.
Шешуі: массасы ізделінетін дене 49-суретте кескінделген. Бұл дененің хОу жазықтығындағы проекциясы АОВ үшбұрышы болады. Айнымалы у-ті ОА кесіндісінде (0≤х≤1 болғанда) бекітсек, х-тің бұл кесіндідегі кез келген бекітілген мәнінде айнымалы у 0 ден х+у=1 түзуінде жатқан нүктенің ординатасына дейін, яғни y=1-x -ке дейін өзгереді (шынында: Оу осіне параллельтүзу интегралдау облысы (D) -ге y=0 түзуі арқылы енеді де, x+y=1 түзуі арқылы облыстан шығады) . Бекітілген х пен у те нүкте вертикальдың бойымен z=0 жазықтығының x+y+z=1 жазықтығына дейін, яғни z=1-x-y -ке дейін ғана қозғала алады.
Айтылғандарды ескеріп, берілген дененің массасын табамыз, ол:
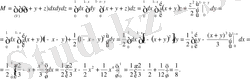
9.
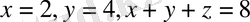 жазықтықтарымен шенелген (шектелген) қиық призманың ауырлық центрін табу керек.
жазықтықтарымен шенелген (шектелген) қиық призманың ауырлық центрін табу керек.
Шешуі: егер дене бір текті, яғни оның тығыздығы тұрақты болса, ондай дененің ауырлық центрінің координаталары
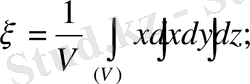
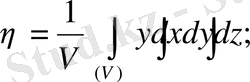
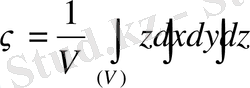
формулалары бойынша табылады.
Ауырлық центрі ізделістегі берілген дене 50-суретте кескінделген.
Әуелі бұл дененің көлемін табамыз. Ол
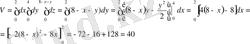
(куб. бірлік) .
Енді ауырлық центрінің координаталарын табу үшін қажет үш еселі интегралдарды есептейміз. Олар:
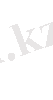
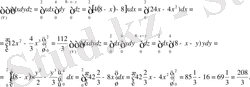
Шыққан нәтижелерді және жоғарыда жазылған формулаларды пайдаланып, ауырлық центрінің координаталарын табамыз, яғни:
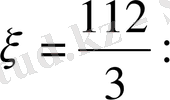
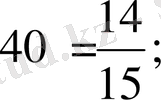
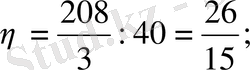
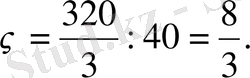
Сөйтіп, берілген қиық призманың ауырлық центрі
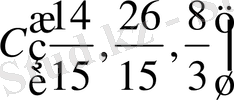 нүктесінде болып шықты.
нүктесінде болып шықты.
Екі еселі интегралдың физикада қолданылуы
Егер пластинка хОу жазықтығының D облысын алып жатса және оның
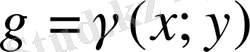 беттік тығыздығы айнымалы болса, онда пластинканың М массасы екі еселі интеграл арқылы былай өрнектеледі:
беттік тығыздығы айнымалы болса, онда пластинканың М массасы екі еселі интеграл арқылы былай өрнектеледі:
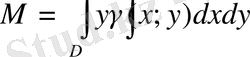
Пластинканың Ох және Оу осьтеріне қатысты статикалық моменті келесі формулалар бойынша табылады:
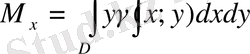
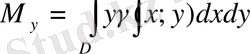
Пластинка біртекті болғанда
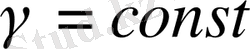 .
.
Пластинканың ауырлық центрінің координаталарын келесі формулалар арқылы есептеуге болады:
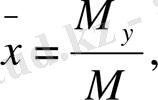
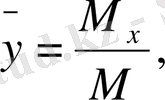
мұнда М - пластинканың массасы, ал М х , М у - оның координаталар осьтеріне қатысты статикалық моменттері.
Пластинка біртекті болса, онда бұл формулалар келесі түрде болады:
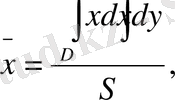
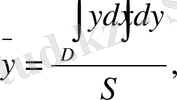
мұнда S - D облысының ауданы.
Пластинканың Ох және Оу осьтеріне қатысты инерция моменттері келесі формулалар бойынша табылады:
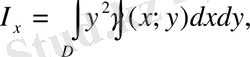
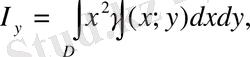
ал координаталар бас нүктесіне қатысты инерция моменті келесі формула бойынша есептеледі:
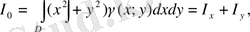
Бұл формулаларда
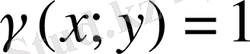 деп алсақ, жазық фигураның геометриялық инерция моменттерін есептеуге арналған формулаларды аламыз.
деп алсақ, жазық фигураның геометриялық инерция моменттерін есептеуге арналған формулаларды аламыз.
Мысалдар:
1. у 2 =4х+4, у 2 =-2х+4 сызықтарымен шектелген фигураның ауырлық центрінің координаталарын анықтаңыз. (16-сурет)
Шешуі: фигура Ох осіне қатысты симметриялы болғандықтан,
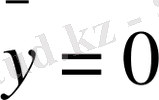 болады.
болады.
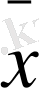 -ті табу керек.
-ті табу керек.
Берілген фигураның ауданын табамыз:

Сонда
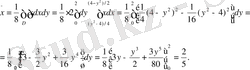
2.
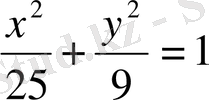 эллипсімен және оның
эллипсімен және оның
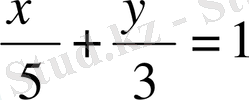 хордасымен шектелген фигураның ауырлық центрінің координаталарын анықтаңыз.
хордасымен шектелген фигураның ауырлық центрінің координаталарын анықтаңыз.
Шешуі: сегменттің ауданын табамыз:
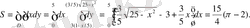
Сонда


3.
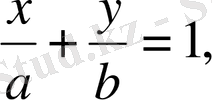

 сызықтарымен шектелген фигураның полярлық инерция моментін анықтаңыз.
сызықтарымен шектелген фигураның полярлық инерция моментін анықтаңыз.
Шешуі: координата бас нүктесіне қатысты иенрция моменті төмендегідей болады:
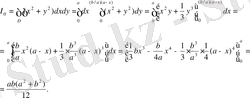
4.
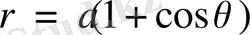 кардиодасымен шектелген фигураның Ох осіне қатысты инерция моментін анықтаңыз.
кардиодасымен шектелген фигураның Ох осіне қатысты инерция моментін анықтаңыз.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz