Екі активті инвестициялар: портфельді оңтайландыру және сызықтық бағдарламалау әдістері


Қазақстан Республикасы білім және ғылым министрлігі
Экономикалық және ақпараттық технологиялар колледжі
Курстық жұмыс
Тақырыбы:
«Екі активті инвестициялар жөнінде есеп»
Орал - 2011 жыл.
Мазмұны:
І. Кіріспе бөлім
1. 1 Кіріспе . . . 3
ІІ. Негізі бөлім
2. 1 Екі активті инвестициялар туралы есептер . . . 4
2. 2 Екі компонентті қоспалар туралы есеп . . . 10
2. 3 Инвестициялар туралы есептер . . . 12
2. 4 Қаржы нарығының негіздері . . . 18
2. 5 Қаржы активтерінің мінездемесі . . . 20
2. 6 Акцияларды бағалау . . . 24
ІІІ. Қорытынды бөлім
3. 1 Қорытынды . . . 26
3. 2 Қолданылған әдебиеттер . . . 27
Кіріспе
Экономикалық жүйелердің әр түрлі деңгейлерінде кездесетін жоспарлау, басқару, шектелген ресурстарды бөлу, өндірістік процестерді талдау, күрделі объектілерді жобалау сияқты есептердің ұтымды және оптимизациялық шешімдерін табу табиғи және ғылыми-техникалық прогресс қажеттіліктерінен туған мәселе.
Жұмыстың сипатына қарай өмірде өзінің кәсібі бойынша әр түрлі құралдарды қолдана отырып, ол қағазға жазып, компьютер арқылы, арнайы бағдарлама арқылы есептің оптималды шешімін жүргізу тиімді. Сондықтан да әр түрлі және жекеленген тәсілдерді білу мен қолдана алу тез әрі оңай қойылған мақсатқа жеткізеді. Тәжірибелік есептерді математикалық әдістермен шығару алгоритмдерін білу және қолдана алу, есептің мәнісін, мағынасын терең түсініп, ұғуға ықпал жасайды.
Оптимизациялық есептердің қойылым түрлері әр түрлі математикалық әдістерді тиімді пайдалануға мүмкіндік береді.
Математикалық әдістерді пайдалану үшін, ең алдымен, тиімді шешімін таппақшы болған есептің өзінің қойылымын жазуымыз қажет. Математикалық қойылымда берілген ресурстар, өндірістік технология, қорытынды шешімдер және олардың арасындағы байланыстар математикалық өрнектер, теңсіздіктер арқылы көрсетіледі.
Екі активті инвестициялар туралы есептер
Инвестиция - бұл пайда табу мақсатында белгілі бір мөлшерде салым салу және осы пайда көзі инфляциялық жоғалтуларды жабуы тиіс.
Инвестордың негізгі мақсаты - инвестицияның табыстылығын және тәуекелділік деңгейін анықтау болып табылады. Инвесторды ең алдымен инвестиция салудың нәтижесіндегі алатын табыс қызықтырады.
Төлемдердің инвестициялық ағындары инвестициялар (шығындар) және пайда болып екіге бөлінеді. Инвестициялардың ең қарапайым мысалын қарастырайық. Инвестор кейбір жұмыс түріне белгілі бір ақша қаражатын іске салады. Нақтылы бір мерзімнен кейін ол іске салған сомманы және сонымен қатар пайыздарды алады. Инвестициялардың пайдалылығын анықтау.
Пайыздар (пайыздық ақша қаражаттары) - бұл белгілі бір мөлшерде және кез келген оның формасында қарызға берілген ақша қаражатынан түсетін табыстың абсолютті шамалары.
Қарыздың қосылған соммасы - бұл бастапқы сомма және мерзімнің аяғындағы есептелген қарыздар пайыздары:
мұндағы S - қарыздың қосылған соммасы; Р - бастапқы қарыздың соммасы; І - мерзімнің аяғына есептелген қарыздар пайызы (кіріс) .
Өсімшенің пайыздық қойылымы (ставкасы) - бұл жылдық пайыздың қарыздық соммасына қатынасы.
Пайыздық қойылым - кез келген қаржы операциясының пайдалылық дәрежесінің өлшеуіші. Бұл жағдайда пайыздық қойылым пайдалылық деп аталады.
Өсімшенің қарапайым пайыздық қойылымы - бұл есептеу базасының қойылымының әрдайым тұрақтылығын қамтамасыз ететін процесс.
(2)
мұндағы Р - қарыздың бастапқы соммасы; n - қарыздың жыл бойынша мерзімі; і - өсімшенің қарапайым пайыздық қойылымы (ондық бөлшек) .
Қаржылық құжаттамаларда өсімшенің пайыздық қойылымы математикалық пайыздар түрінде беріледі. Мысалы, өсімшенің қойылымы 20% тең деп оқып шығуға болады. Формулаға 20-ны 100-ге бөлгендегі пайда болатын 0, 2 санын қоюға болады.
(3)
Мына
(4)
мұндағы t - қарыз күндерінің саны; К - уақытша база немесе жылдағы күндер саны.
Қабылданған әдістемеге байланысты уақытша базаның екі түрін қолданады:
1. Қарапайым пайыздық есептеуде - К = 360;
2. Дәл пайыздық есептеуде - К = 365(366) .
1 - мысал. 28000 тг. көлеміндегі қарыз Жылдық қарапайым 16% пайызбен 185 күнге берілді. 360 және 365 күнге уақытша базадағы пайызды және арттыру соммасын анықтау.
Ш е ш у і. Жылдық мерзімді (4) формуламен анықтаймыз, ал пайыздардың шамасын - (2) формула бойынша:
- Қарапайым пайыздар үшін (2) сәйкес:
- Дәл пайыздар үшін:
Арттыру соммасын (1) формула бойынша табамыз:
- Қарапайым пайыздар үшін:
- Дәл пайыздар үшін:
Өсімшенің күрделі пайыздық қойылымы - бұл есептеу базасының қойылымының айнымалы болуы, яғни пайыздар пайыздарға есептеліп қойылады.
Күрделі пайыздың формуласы мына түрде болады:
мұндағы S - арттыру соммасы; Р - қарыздың бастапқы соммасы; n - жылдық қарыз соммасы; і - күрделі жылдық пайыздық арттыру қойылымы (ондық бөлшек) .
Белгілі бір шығындарға арналған ақшалай соммалар бюджеттік шектеулер деп аталады.
Екі түрлі акцияларға инвестиция салу жағдайларын қарастырайық. S бюджеттік шектеуі бірінші р 1 және екінші р 2 акцияларының бағаларымен байланысқан:
Бюджеттік шектеуден тыс инвестор шектеуді тәуекел шамасынан жоғары қояды.
Тәуекелді сипаттаудың бір әдісін қарап көрейік.
Инвестор жүзеге асыруға қажетті қаржылық операциялардың пайдалылығы кездейсоқ мән болып табылады. Инвестор белгілі бір жобаға инвестиция сала отырып, оның пайдалылығының шамасын алдын ала білмейді. Мысалы, инвестор акцияны сатып алу барысында, оны иелену кезіндегі пайдалылығын кейбір белгілерге байланысты тек қана шамамен жори алады.
Әдетте кездейсоқ шама - тарату заңы немесе осы заңның моменттерімен суреттеледі. Ең алғашқы моменттерді қарастырайық: математикалық күтім және дисперсия.
Математикалық күтім (орташа таңдаулы мән) күтілетін кездейсоқ шаманың ең ықтимал мәндерін анықтайды, мысалы пайдалылығын. Егер инвестициялық жобаның барлық кездейсоқ бастапқы шамалары дұрыс таңдалған болса, онда, бұл шамалардың математикалық күтімі болып табылады.
Дисперсия және орташа квадраттық ауытқу математикалық күтімге қатысты кездейсоқ шаманың шашылуымен сипатталады. Дисперсияның немесе орташа квадраттық ауытқудың шамасы неғұрлым көп болса, шашылу соғұрлым көп болады. Мысалы, екі топ оқушыларының орташа жас шамасы 25 жасқа тең. Бірінші топтағы жастың орташа квадраттық ауытқуы 1, 2 жылға тең, екінші топтағы - 2, 8 жыл. Осыдан оқушылардың жас бойынша шашылуы екінші топта көбірек екені анықталады. Байқайтын болсақ, дисперсияны орташа квадраттық ауытқуды шаршыға шығару арқылы табамыз. Математикалық күтім және орташа квадраттық ауытқу ылғи да бірдей өлшемдерде болатынын есте сақтау керек.
Көп жағдайда орташа квадраттық ауытқу тәуекелділік шара ретінде таңдалады. Мұндай таңдаудың заңдылығын дәлелдейік.
1 - суретте пайдалылықтың екі кездейсоқ процесстеріндегі f(q) тығыздықты үлестіру ықтималдылығы көрсетілген.
Сондықтан бірінші жоба екінші жобаға қарағанда кіші тәуекел деңгейге ие. Келтірілген пікірлер жобаның пайдалылығының тәуекел шарасы ретінде үйреншікті ауытқу қызмет көрсете алады деген қорытынды жасауға мүмкіндік береді.
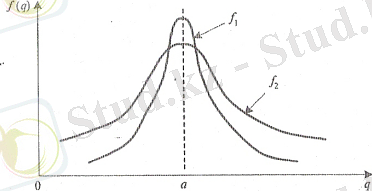
1 - cурет.
Акцияның екі түрін сатып алуға қайтып оралайық. Инвестор тәуекелді шектеуге тырысады. Орташа квадраттық ауытқу мен күтілетін пайдалылықтың шамалары бірдей өлшемге ие болатындықтан, тәуекелділікті таңдауда оны пайдалылықпен салыстырады. Егер акцияның күтілетін пайдалылығын і арқылы белгілесек, онда көрсетілген шектеуді мына түрде жазуға болады:
мұндағы K - коэфициент, инвестордың тәуекелге бағыты (неғұрлым инвестордың тәуекелге бағыты көп болса, соғұрлым берілген коэфициент те үлкен болады) ; p - акцияның бағасы; х - осы түрдегі акциялардың алынатын саны; S - акцияның барлық түрін сатып алуға арналған ақша соммасы;
K -ның үлкеюі, басқа да осындай жағдайларда инвестор акцияны
Бағалы қағаздар портфелінің ұтымды құрамын анықтау үшін арналған сызықтық бағдарламалаудың есебін белгіленген шектеулер бойынша төмендегіше құрастырылуы мүмкін.
Мақсаттық функция инвестициялық портфельдегі мәліметтердің әкелетін пайдасымен анықталады, және мынадай түрде болады:
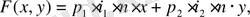
мұндағы p 1 , p 2 - акцияның бірінші және екінші түрлерінің нарықтық бағасы; і 1 , і 2 - акцияның бірінші және екінші түрлерінен күтілетін пайда; n - операциялардың жыл бойынша мерзімі; x , y - инвестициялық портфельдегі акциялардың бірінші және екінші түрлерінің саны.
Бюджеттік шектеу (8) формуламен анықталады.
Тәуекел бойынша шектеуді мына түрде жазу ыңғайлы:
(7)
мұндағы
3 - мысал. Кестеде көрсетілген сипаттамалар бойынша акцияның екі түрінің І және ІІ портфелін құрастыру үшін 5 мың тг. бөлінген. Инвестордың акцияның бірінші және екінші түрлеріне қатысты тәуекел коэффициенті 5-ке тең.
1 - кесте.
Күтілетін
пайда
%
Акцияның нарықтық бағасы
тг.
І
ІІ
12
20
18
23
25
20
Жыл бойынша осы портфельден күтілетін пайда және портфельдің ұтымды құрамын анықтау.
Ш е ш у і. Сызықтық бағдарламалау есебі мынадай түрде болады:
мына шектеулерге
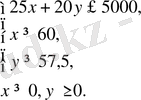
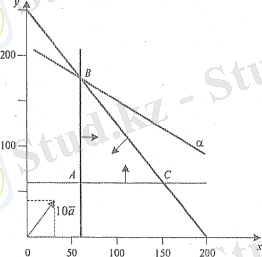
2 - сурет.
Сонымен, 880 тг. тең ең көп мөлшердегі күтілетін пайда түсіру үшін инвестор бірінші түрдегі 60 акцияны және екінші түрдегі 175 акцияны сатып алуы керек.
Екі компонентті қоспалар туралы есеп
Берілген құрамдағы қоспаны алу мақсатында әртүрлі компоненттерді ұтымды пайдалану кезінде қоспалар туралы есепті шешуге тура келеді. Мұндай есептер мал шаруашылығында мал азығын рациондау, тамақ өнеркәсібінің, жеңіл өнеркәсіп, парфюмерия өнімдерінің құрамын анықтауда көптеп кездеседі.
Қоспалар туралы есептер бір және көпөнімді болып бөлінеді. Өнімдерге шектеу қойылады. Берілген шектеулермен қоспаны өндіруге жұмсалатын шығын немесе алынатын пайда оптималдандырылады. Шығынды оптималдау кезінде есеп минимумға, ал кірісті оптималдауда максимумға шығарылады.
4 - мысал. Мал шаруашылығы фермасы араластыру арқылы A , B және C дәрумендері бар бірінші және екінші түрдегі екі компоненті жем шығарады. Бірінші түрдегі бір компонент құны - 1 тг., екінші түрдегі бір компонент құны - 2 тг. 1 кг. компоненттің әр түріндегі дәрумендер құрамы мен олардың күндік рациондағы минималды нормасы (мөлшері) төмендегі кестеде көрсетілген.
2 - кесте.
A
B
C
20
18
9
8
4
-
4
6
6
Ең төменгі құнға ие күндік рационды құру.
Ш е ш у і. Егер күндізгі рационға кіретін х - бірінші түрдегі компоненттердің саны, ал y - екінші түрдегі компоненттердің саны болса, онда сызықтық бағдарламалау есебін мына түрде жазуға болады:
мына шектеулерге
Сонымен, ең көп мөлшерде 1 421 176 тг. тең пайда табу үшін, мекеме бірінші түрдегі заттың - 2000 кг., екінші түрдегі заттың - 212 кг., үшінші түрдегі заттың - 294 кг. өндіріп шығаруы тиіс.
Инвестициялар туралы есептер
Әдетте, портфель бағалы қағаздардың бірнеше түрі арқылы құрастырылады және олардың саны екеуден көп болады.
5 - мысал. Сипаттамалары төмендегі кестеде көрсетілгендей І, ІІ және ІІІ үш түрлі акциялар бар. Осы акциялар арқылы портфель құрастыру үшін 5 мың тг. бөлінген. Инвестордың бірінші, екінші және үшінші түріне бейім тәуекел коэффициенты беске тең.
Күтілетін пайда
%
Пайданың орташа квадраттық ауытқуы
%
І
ІІ
ІІІ
12
20
24
18
23
30
25
20
10
3 - кесте.
Осы портфельдың жылдық портфель құрамын және күтілетін пайданы анықтау.
Ш е ш у і. Бір акциядан түсетін пайда (1. 14) формуласы бойынша анықталады. Сызықтық бағдарламалау есебі мынадай түрде болады:
мына шектеулерге
Есепті канондық түрге келтіреміз және оны минимумды табу мақсатында көрсетеміз:
мына шектеулерге
Негіз ретінде мынаны таңдаймыз
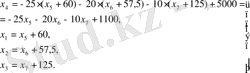 (9)
(9)
Мақсаттық функция мына түрде болады:
(10)
Мақсаттық функция белгісіз еркін коэфициенттер барысында теріс болғандықтан, негіздеуішті келесі негіздеуішке алмастырамыз. Сонда есептің 3 жағдайына ие боламыз.
Мақсаттық функцияда х 6 және х 7 үшін коэффициенттер теріс болып келеді. Сонымен қатар бірінші және екінші теңсіздіктердегі мүмкін болатын түрдегі х 6 және х 7 жүйелері коэффициенттері де теріс. Сондықтан да есепті шешуге болатын 3 мүмкін жағдайға ие боламыз.
х 4 = x 7 = 0 үшін х 6 мәнін жетілдіру тәсілін орындаймыз.
Енді х 6 мәнін мақсаттық функция теңсіздігінің мүмкін болатын жүйесіне қоямыз:
(15) мақсаттық функциядағы коэффициент х 7 үшін теріс таңбалы. x 5 = x 4 =0 үшін х 7 мәнін жетілдіреміз:
х 7 үлкейту барысында х 6 және х 2 айнымалылары нольге айналады: бірінші жүйе теңсіздігі үшін х 7 = 110, үшінші үшін х 7 = 225. Cондықтан
х 7 мәнін (15) мақсаттық функциясына және мүмкін болатын (16) жүйе теңсіздігіне қоя отырып, сызықтық бағдарламалауды мына түрге келтіреміз:
мына шектеулерге
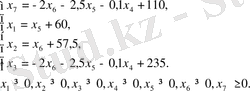
F мақсаттық функциясы үшін белгісіз базистік емес мәндер теріс болғандықтан, біз есептің 1 жағдайына ие боламыз. х 1 =60, x 2 =57, 5, x 3 =235 базистік шешімдері оптимальды болып табылады.
Басынан бастап берілген есеп ең үлкен мәнді табуға байланысты бағытталғандықтан, мақсаттық функцияның максимальды мәні берілген шектеулерге байланысты:
F max = 974.
Cондықтан, төмендегідей қорытынды келтіруге болады: бірінші типті 60 акция, екінші типті 57(58) акция және үшінші типті 235 акция сатып алғанда инвестордың жылдық күтім пайдасы 974 теңгені құрайды.
6 - мысал. Менеджер әртүрлі кәсіпорындарға 1 доллар ақша қаражатын кредит ретінде бөліп орналастырмақшы. Менеджер жылдық табыстан келісілген пайыз мөлшерінде келетін ақшадан максимальды пайда табу үшін, осы кредитті әр кәсіпорынға тиімді орналастыру жоспарын құруы керек.
Кәсіпорындардың аттарын: А, В, С, Д деп белгілейік. Келісім-шарт бойынша, әр кәсіпорын жылдық табыстың мынадай пайыздарын қайтаруға міндетті:
А - 6 % , B - 8 % , C - 10 % және Д - 9 % . Сонымен қатар әр кәсіпорында қауіпсіздік немесе тәуекелділік дәрежесі, капиталдың қайтымы, басқа нарық жағдайлары, мысалға, салық төлеу саясаты және т. б. түрлері белгілі болсын.
Инвестиция жұмысының қауіпсіздігін азайту үшін, менеджер капиталдың жартысынан кем емес бөлігін А және В кәсіпорындарына орналастыруға, соынмен қатар капиталдың қайтымдылығын (ликвидность) қамтамасыз ету үшін, барлық ақшаның 25%-дан астам бөлігін Д кәсіпорнына орналастыруға шешім қабылдады. Өкіметтің саясатының өзгеруіне байланысты С кәсіпорнына 20%-дан аспайтын, ал салық саясатының ерекшелігіне байланысты, барлық капиталдың 30%-дан кем емес бөлігін А кәсіпорнына орналастыру керек.
Ш е ш у і. Әр кәсіпорынға бөлінген оптималды инвестиция мөлшерін: А - Х 1 мың доллар, В - Х 2 мың доллар, С - Х 3 мың доллар және Д - Х 4 мың доллар деп белгілейік.
Барлық кәсіпорынның жылдық табысынан бөлінген пайыздан түсетін ақшаның өлшем бірлігіндегі мөлшері максималды болуы қажет, яғни:
\[Z=0.06X_{1}+0.08X_{2}+0.10X_{3}+0.09X_{4}.\]
Сонымен қатар мынадай шарттар орындалуға тиіс:
- барлық инвестиция мөлшері:
- инвестиция қауіпсіздігін (риск) қамтамасыз ету:
- капиталдың қайтымдылығын (ликвидность) қамтамасыз ету:
- өкіметтің саясаты бойынша:
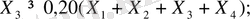
- салық салу саясаты бойынша:
- белгісіздердің теріс болмау шарты:
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz