Pascal программалау тілінде математикалық маятник тербелісін моделдеу

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 21 бет
Таңдаулыға:

Мазмұны
Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...3
... ... ... ... ... ... ... ... .. ... ... ... ... .
1. Математикалық маятник тербелісі және оның түрлері,
заңдылықтары ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ...5
... ... ... ... ... ... ... ... .. ... ...
1.1 Маятниктің қозғалыс заңы және Эйлер 5
әдісі ... ... ... ... ... ... ... . ... ... ... ... ..
1.2 Математикалық маятник және гармоникалық 8
тербелістер ... ... ... ... ... ... .
1.3 Айналмалы математикалық 11
маятник ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
2. Pascal программалау тілінде математикалық маятник тербелісін
моделдеу ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ...14
... ... ... ... ... ... ... ... .. ... ... ... ...
2.1 Математикалық маятниктің epкiн тербелісін 14
моделдеу ... ... ... ... ... ... .. ...
2.2 Математикалық маятниктің epкiн тербелісін 16
моделдеу ... ... ... ... ... ... .. ...
Қорытынды ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ...25
... ... ... ... ... ... ... ... .. ... ... ..
Қолданылған 27
әдебиеттер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
... ... ... ... ... ..

Кіріспе

Қазіргі кезде кеңінен қолданылатын программалау жүйесінің негізі Турбо
Паскаль. Кез-келген программалау тілінде, соның ішінде Турбо Паскальда әр
түрлі деңгейдегі есептерді шығаруда программалар құру үшін әр түрлі
программалау жүйелері қолданылады.
Қарастырылып отырған курстық жұмыс программалау тілдері пәндерінің
көмегімен “Математикалық маятник тербелісін моделдеу” тақырыбын зерттейді.
Аталған тақырып бойынша математикалық маятниктердің түрлері, олардың
тербеліс заңдары туралы нақты айтылады.
Курстық жұмыстың мақсаты: Паскаль программалау тілінде математикалық
маятник тербелісін моделдеу және оны зерттеу болып табылады. Курстық
жұмыстың орындалуы graph, crt модульдерінің және циклдік құрылымдардың
көмегімен жүзеге асты. Математикалық маятник тербелісін моделдеуде графика
маңызды роль атқарады, себебі суреттер және графикалар мұндай
программалардың көмегінсіз жүзеге аспайтын еді. Маятник тербелісін
моделдеуді орындау жұмыстары кезінде CRT.TPU және GRAPH.TPU стандартты
модульдері қолданылды. Олардың алғашқысы енгізу-шығару процедуралары болса,
екіншісі – стандартты графикалық процедуралардың пакетінен болып табылады.
OpenGraph процедурасы 640х480 өлшемді монитор жұмысының графикалық
режимдегі жұмысын анықтайды. Display процедурасы экранды алдыңғы өткен
суреттен тазартып, келесісін шығарып отыруды қамтамасыз етеді. Программаның
негізгі бөлімінде алдымен монитор жұмысының графикалық режимдегі жұмысы
инициализациялауда InitGraph қолданылады.
Кез келген сурет жеткілікті түрде қарапайым геометриялық фигуралардан
құралады. Олар нүкте, түзулер қимасы, шеңберлер және тағы басқалар.
Геометриялық обьектілердің орны мен пішіні нүктенің координаталарымен
берілетіндігі геометриядан белгілі. Өз кезегінде, графикалық қорытындыны
программалау үшін графикалық обьектілердің координаталарын беруді үйрену
қажет. Көптеген процедуралар мен функциялар экрандағы қадамын бағыттаушыны
қолданады, оның ерекшелігі мәтіндік курсорға қарағанда көрінбейді. Бұл
бағыттаушының орны экрандағы кез келген координата секілді сол жақ жоғарғы
бұрышқа қатысты координаталарға ие болады. Осылайша экранның тігінен
орналасқан координатасы солдан оңға қарай өседі, ал көлденең орналасқан
координата жоғарыдан төменге қарай өседі.
Курстық жұмыстың міндеттері:
• Маятник және оның түрлері туралы ақпаратты игеру;
• Паскаль программалау тіліндегі математикалық маятник тербелісін
моделдеуге қатысты графиканың мүмкіндіктерін зерттеу;
• Graph және Crt модулдерін пайдалану арқылы программа құру;
• Математикалық маятник тербелісін моделдеудің негізгі ерекшеліктерін
зерттеу;
• Математикалық маятник тербелісін моделдеу тақырыбына есептер шығару.
Қазіргі таңда Галилейдің собордағы мінәжат ету кезінде қола аспашамның
тербелуін мұқият бақылағандығы туралы аңызға сену қиын. Ол аспашамның әрлі-
берлі қозғалуына кеткен уақытты бақылап және анықтап отырған. Бұл уақытты
кейін тербеліс периоды деп атап кеткен. Галилейде сағат болмаған, сондықтан
әр түрлі ұзындықтағы шынжырларға ілінген аспашамның тербеліс периодын
салыстыру үшін өзінің пульсінің соғу жиілігін қолданды. Кез келген маятник
толық анықталған тербеліс периодынан тұрғандықтан, оларды сағат жүрісін
реттеп отыру үшін пайдаланады. Сонымен қатар, маятник геологиялық барлау
жұмыстары кезінде маңызды орын алады. Жер шарының әр түрлі жерлерінде g
мәні әр түлі болатындығы белгілі. Оған қоса, кендер көптеп орналасқан
жерлерде g аномальді жоғары болып келеді, оған кейбір металл қазбалары
мысал бола алады.
Математикалық маятник деп салмағы дененің салмағына қарағанда
әлдеқайда кем жіңішке созылмайтын жіпке ілінген шағын көлемдегі денені
айтады.

1. Математикалық маятник тербелісі және оның түрлері, заңдылықтары
1.1 Маятниктің қозғалыс заңы және Эйлер әдісі

Математикалық маятник – механикалық жүйеден құралған, созылмайтын
салмақсыз жіпте немесе салмақсыз стерженьде орналасқан материалдық нүктеден
тұратын осциллятор.
Маятниктің аз бұрылу қозғалысы – белгілі гармониялық тербелістер.
Маятниктің қозғалыс заңы келесі түрде жазылады:
x=acos(+)
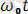
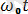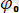
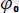(1)
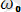
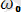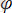
мұнда - тербелістің жиілігі, a - амплитуда, 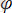- бастапқы
фаза. Егер бұрылулар аз болмаса, тербелістерді сипаттайтын теңдеу.
Маятниктің қозғалысының зерттеу нәтижелерін (x,v) жазықтықта қисықтар
жиыны ретінде салу ыңғайлы, мұнда v=x – бұрыштың өзгеру жылдамдығы, (x,v)
жазықтығы фазалық жазықтық деп, ал x=x(t), v=v(t) (2) параметрлік қозғалыс
заңымен анықталатын қисықтар - фазалық траекториялар деп аталады.
Сызықты осциллятордың фазалық траекториялары энергияның сақтау заңымен
анықталатын эллипс болады. Математикалық маятник үшін бұл аз бұрылу бұрышы
кезінде дұрыс. Үлкен бұрылу бұрышы кезінде математикалық маятниктің
қозғалысы күрделі болады: маятник тербеліс жазықтығынан басқа жан-жаққа
айналу мүмкін.
(2)-теңдеудің аналитикалық шешімі өте күрделі болғандықтан, маятниктің
қозғалысы сандық түрде зерттеледі. (2)-теңдеудің бірінші ретті теңдеулер
жүйесі ретінде жазылуы:
x=v,
v=-w02sinx
(3)
Кәдімгі дифференциалдық теңдеулерді (КДТ) сандық түрде шешкенде [1]
бастапқы дифференциалдық теңдеулер орнына шекті-айрымды КДТ шешімі
табылады. Шекті-айрымды теңдеулерге өту келесі түрде жүргізіледі. Туындының
дәл мәнінің орнына оның айырымдық аналогы қарастырылады
,
.
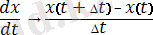
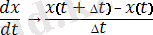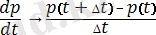
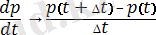(4)
мұнда мейлінше аз шама. Соңғы айырымдар арқылы (3)-жүйе келесі
түрде жазылады:
,
,
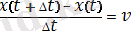
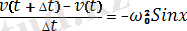
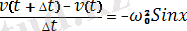(5)
Бұдан нүктесінде координаттар мен жылдамдықтың мәндерін табуға
арналған формулалар алынады:
,
.
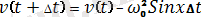
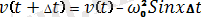(6)
Осындай есептеулерді көп рет қайталап, x(t) және v(t) тәуелділіктерді
табуға болады, осындай әдіс жанама әдісі немесе Эйлер әдісі деп аталады.
Бағдарламаны құруға кірісуден бұрын, қолданатын бағдарламалау тіліне
сай, есепті тәуелсіз тапсырмалар тізбегіне бөлу керек, яғни алгоритм
құрастырылады. Берілген есеп шешімінің бағдарламасы келесі бөліктерден тұру
керек:
1. Бастапқы шарттарды белгілеу.
2. Функцияны белгілеу.
3. Бойында шешім табылатын кесіндіні және интегралдау қадамын беру
(интегралдау қадамын беруден гөрі интегралдау кесіндісі бөлінетін
интервалдар санын беріп, қадамның мәнін есептеу ыңғайлы).
4. Дифференциалдық теңдеудің шешімдері анықталатын нүктелердің
координаттарын есептеу.
5. Зерттелетін теңдеуді шешу.
6. Нәтижені шығару.
Эйлер әдісінің дәлдік бойынша шектелулері бар. Дәлірек 4-ретті Рунге-
Кутт әдісі болып табылады. Бүл әдіс келесі итерациялық формуламен жүзеге
асырылады:
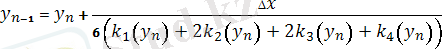
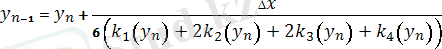(7)
мұндағы k1, k2, k3, k4 - мына формулалармен есептелетін түзетулер
,
,
,
.
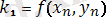
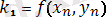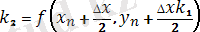
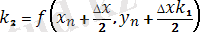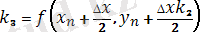
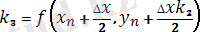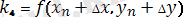
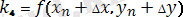(8)
MatLab пакетінде кәдімгі дифференциалдық теңдеулерді 4-ретті Рунге-
Кутт әдісімен шешу ode45 функциясымен іске асырылған [2]. Төменде MatLab
тілінде (3)-кәдімгі дифференциалдық теңдеулер жүйесінднің оң жағындағы
функцияның анықтамасы келтірілген oscil атты файл-функция, маятниктің
қозғалыс теңдеуін сандық шешуге және бейнелеуге арналған программаның
мәтіндері берілген.
% oscil.т файл-функцияның листингі function F=oscil(t,y)
% (3)-КДТ жүйесіндегі оң жағындағы % функцияны анықтау, global omega;
F=[у(2); -omega^2tsin(y(1))];
Файл-функцияны дискде міндетті түрде oscil. атымен сақтау қажет. Әрі
қарай программаның өзі жазылады:
% маятниктің қозғалыс теңдеуін сандық шешуге
% және бейнелеуге арналған программаның листингі
% айнымалыны ауқымды жариялау global omega;
% х(0)=2, бастапқы шарттарды беру
Ү0=[2;3];
%х және мәндерін табу және экранға
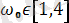
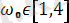кезіндегі
% бейсызық маятниктің фазалық портреттің қисықтар үйірін
% шығару for omega=1:0.3:4
[T,Y]=ode45{‘oscir,[0:0.005:4*pi],Y 0);
% oscil - функцияның анықтамасы бар файл-функцияның аты;
% [0:0.Ö05:4*pi] - интегралдау интервалын анықтайтын вектор;
% хО - бастапқы шарттар векторы
plot(T, Ү(;11),’г’) % x(t) графигі grid on
xlabel('t'); % абсцисса өсінің аты
ylabel (‘х’); % ордината өсінің аты
end
figure(2);
plot(Y(:,1),Y{:,2),’k’); % (х) графигі
figure(3);
plot(T,Y(:,2);kJ);
% графигі

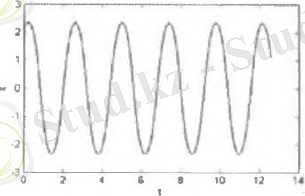
Сурет 1. Координатаның уақытқа тәуелді сызбасы

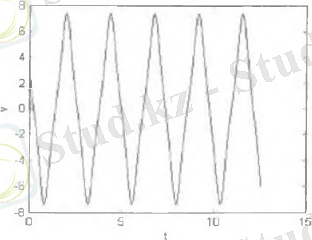
Сурет 2. Тербеліс жылдамдығының уақытқа тәуелді сызбасы

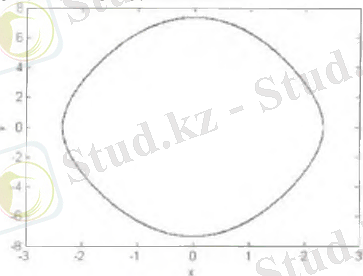
Сурет 3. Фазалық портрет

1.2 Математикалық маятник және гармоникалық тербелістер

Математикалық маятник деп салмағы дененің салмағына қарағанда
әлдеқайда кем жіңішке созылмайтын жіпке ілінген шағын көлемдегі денені
айтады.
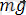
Маятник тепе-теңдік жағдайында 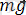ауырлық күші жіптің керілу күшіне
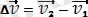
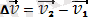тең болады.
(9)
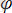
Маятниктің тепе-теңдік жағдайынан кейбір 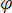бұрыштарға бұрылу
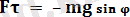
кезінде 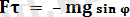ауырлық күшіне тең жанама пайда болады (сурет 4).
(10)
Бұл формуладағы минус таңбасы жанаманың маятниктің бұрылу бағытына
қарама-қарсы бағытталғандығын білдіреді.

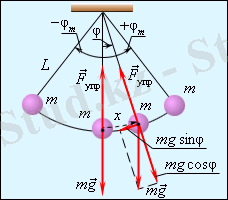
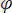
Сурет 4. Математикалық маятник. 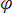– маятниктің тепе-теңдік
жағдайынан бұрыштық бұрылуы, – маятниктің доғасы бойынша ығысуы

Егер радиусы l шеңбердің доғасы бойынша тепе-теңдік жағдайында тұрған
маятниктің сызықтық ығысуын х арқылы белгілесе, онда оның бұрыштық ығысуы
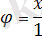
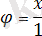. Жанамаға бағытталған үдеу мен күштің векторлы проекциялары үшін
жазылған Ньютонның екінші заңы келесі формуланы береді:

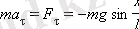(11)
Бұл қатынас математикалық маятниктің, маятникті тепе-теңдік күйіне
келтіруге талпынған күш секілді, күрделі сызықтық емес жүйе екендігін
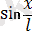
көрсетеді. Тек шағын тербеліс кезінде 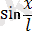мәнін мәніне жуықтап
алмастыруға болатын болса, онда математикалық маятник гармоникалық
осциллятор болып табылады, яғни гармоникалық тербелістер жасай алатын жүйе
ретінде қарастырылады. Тәжірибе жүзінде мұндай жуықтаулар 15–20°
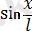
шамасындағы бұрышытар үшін әділ болады, сол кезде 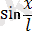шамасының
қарағанда 2 % өзгешелігі бар. Жоғары амплитуда кезіндегі маятниктің
тербелісі гармоникалық болып табылмайды. Математикалық маятниктің шағын
тербелістері үшін Ньютонның екінші заңы мына түрде жазылады:
.
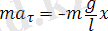
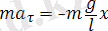(12)
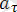
Осылайша, маятниктің 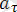тангенстік үдеуі оның кері шамада алған х
ығысуына тура пропорционал. Бұл жүйенің гармоникалық осциллятор болып
табылатын шарты. Барлық жүйелер үшін жалпы ережес бойынша еркін
гармоникалық тербеліс жасау мүмкіншілігі үдеу мен тепе-теңдік күйіндегі
ығысудың арасындағы пропорционалдық коэффициентінің модулі айнымалы
жиіліктің квадратына тең:
; .
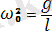
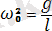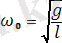
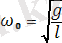(13)
Бұл формула математикалық маятниктің шағын тербелісінің меншікті
жиілігін береді. Осы формулаға сәйкес келесісі орындалады:
.
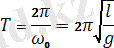
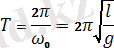(14)
Ауырлық өрісінде еркін тербеліс жасай алатын, айналмалы көлденең осьте
орналасқан кез келген дене маятник болып табылады. Мұндай маятниктер
физикалық деп аталады (сурет 5). Ол математикалық маятниктен массасының
реті бойынша ерекшеленеді. Физикалық маятникттің нық тепе-теңдіктегі
массасының центрі С ось арқылы өтетін тігінен орналасқан О айналу осінің
төменгі жағында орналасқан.
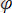
Маятникті 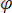бұрышына бұру кезінде маятникті тепе-теңдік күйіне
келтіруге тырысатын ауырлық күшінің моменті туындайды:
M = –(mg sin φ)d.
(15)
Мұндағы d – айналу осі мен С массасының центрі арасындағы арақашықтық.

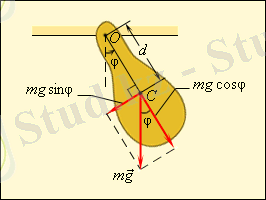
Сурет 5. Физикалық маятник

Формуладағы минус таңбасы әдеттегідей күш моменті маятникті тепе-
теңдік күйінен қарама-қарсы бағытқа бұруға тырысады. Математикалық
маятниктің жағдайындағыдай М қайтару моменті sin φ мәніне пропорционал
болады. Бұл физикалық маятниктің тек sin φ ≈ φ, яғни бұрышы кіші болған
кезінде ғана еркін гармониялық тербелістер жасауға мүмкіндігі бар екендігін
көрсетеді. Аз тербеліс кезінде:
M = –mgdφ.
(16)
Сызықтық емес маятник. Үлкен амплитудамен тербелетін маятниктің қозғалыс
заңы қиынырақ болып келеді:

(17)

мұндағы  — бұл Якоби синусы,  периодтық функция болып табылады,
жанындағы аз  қарапайым тригонометриялық синуспен сәйкес келеді.
параметрі мына өрнек арқылы орындалады:

(18)
иұнда —t−2 бірлігіндегі маятник энергиясы
Сызықтық емес маятник тербелісінің периоды.

(19)
мұнда K — бірінші түрі эллиптикалық интеграл.
Тәжірибе жүзінде есептеуде эллиптикалық интегралды қатарға жіктеген
ыңғайлы:

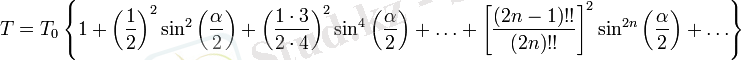
(20)
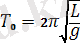
мұнда 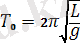— шағын тербеліс периоды,  — маятниктің тігінен ауытқу
бұрышы.
1 радианға дейінгі бұрыштарда (≈60°) қолайлы дәлдікпен (қателік шамамен
1 %)) бірінші жуықтауды қолдануға болады:
.
(21)
Егер ауытқыған маятник бастапқы жылдамдығын хабарласа, онда С нуктесі
сферада екі параллель арасына алынған z = z1 және z = z2 l радиусты
сипаттайтын болады, ал z1 және z2 (сурет 5) алғашқы шарттарға тәуелді болып
келеді (сфералық маятник). Жеке жағдайда z1 = z2 болғанда (сурет 6) С
нүктесі шеңберді көлденең жазықтықта сипаттайтын болады. Айналмалы емес
маятниктердің ішіндегі циклоидалдық маятникке назар аударыла бастады,
олардың барлық тербелістері кез келген мөлшердегі амплитудаға қарамастан
изохронды.
Физикалық маятник аспаның айналасындағы көлденең ось ауырлық күшінің
әсерінен істейтін қатты дене деп аталады. Аз бұрылу салдарынан маятник
гармоникалыққа жақын периодтты тербеліс жасайды.

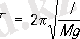(22)
мұндағы l маятниктің аспалы осіне қатысты инерция моменті, l – аспаның
осіне О ауырлық центріне дейінгі арақашықтық. Физикалық маятниктің тербеліс
периоды ұзындығы l0 = IMl болатын математикалық маятниктің тербеліс
периодымен сәйкес келеді. Бұл ұзындық берілген физикалық маятниктің
реттелген ұзындығы болып табылады.
Аспаның осінен l0 қашықтықта орналасқан К нүктесі түзуінің жалғасы OC
физикалық маятниктің тербеліс центрі деп аталады. Осы кезде
OK = l0 арақашықтығы OC = l қарағанда улкен болады.
Маятник құрамы түрлі құрылғыларда қолданылады, мысалы, сағаттар, еркін
түсу удеуін анықтайтын құралғы (маятникалық құрылғы), жедел қозғалатын
денелер, гиперскопикалық құрылғылар, дененің инерциялық моментін
эксперементалды анықтайтын құралдар және тағы басқалары.

1.3 Айналмалы математикалық маятник

Маятник – қозғалмайтын нүктенің немесе осьтің айналасында күшпен
(әдетте ауырлық күші) әсер ету нәтижесінде тербеліс жасайтын дене.
Қарапайым маятник жіңішке стерженьге ілінген жүктен тұрады. Егер стерженьді
созылмайтын болса әрі стерженьнің ұзындығымен салыстырғанда жүктің көлемін,
ал стерженьнің салмағын жүктің массасымен салыстырғанда кемітетін болса,
онда мұндай жүйені О ілінген нүктесінен l қалыпты арақашықтықта орналасқан
m салмағы бар материалдық нүкте деп қарастыруға болады. Бұл идеалданған
маятник математикалық деп аталады.
Егер тепе-теңдік қалпынан бұрылған маятникті жіберетін болса, онда ол
бір тік жазықтықта тербелетін болады, ал оның ауырлық центрі шеңбердің
доғасы бойымен қозғалады. Бұл жағдайда маятникті математикалық жазық немесе
айналмалы деп атайды және оның кеңістіктегі орны бір координатамен
анықталады. Аталған жүйені бір дәрежелі еркін жүйелер деп атайды.
Егер байланысқан күштердің әсерінен материалдық нүкте берілген
қисықпен жүруге мәжбүр болған кезде, нүктенің қозғалысы еркін болмайды.

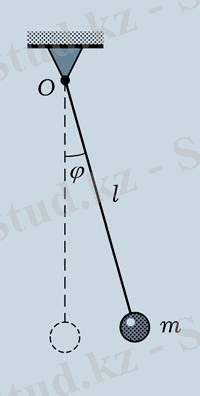
Сурет 6. Айналмалы математикалық маятник

Ортақ айналу осі бар екі математикалық маятник. Бұл жағдайда бірдей
ұзындыққа ие және ортақ іліну нүктесі бар екі айналмалы маятниктен тұратын
жүйе қарастырылады. Маятниктер бір-бірімен соғылуына бақылау жүргізе отырып
тік жазықтықта тербеледі.

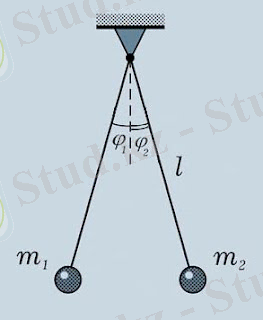
Сурет 7. Ортақ айналу осі бар екі математикалық маятник

Серпімді байланыстағы екі математикалық маятник. Аталған тербелмелі
жүйе бір тік жазықтықта тербелетін бірдей немесе әр түрлі ұзындық пен
массалардан тұратын екі айналмалы математикалық маятникті береді. Маятник
серпімді байланыстан тұрады, олардың іліну нүктелері бір көлденең сызықта
орналасқан.

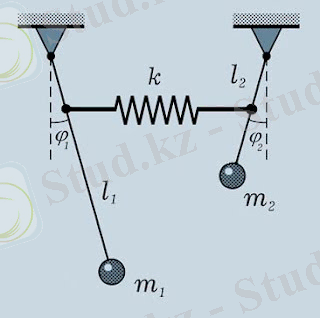
Сурет 8. Серпімді байланыстағы екі математикалық маятник

2. Pascal программалау тілінде математикалық маятник тербелісін
моделдеу
2.1 Математикалық маятниктің epкiн тербелісін моделдеу

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.