Есептің математикалық моделін құру

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 16 бет
Таңдаулыға:

Жоспар

Кіріспе3

I. Сызықтық бағдарламалау әдістері мен модельдері4

1. 1 Сызықтық бағдарламалау элеметтері4

1. 2 Сызықтық бағдарламалау есептерінің модельдерінің түрлері және құру жолдары6

1. 3 Симплекс әдісінің негіздері8

II. Сызықтық бағдарламалау есептерін шешу10

2. 1 Тәжірибиелік операциядағы есептің қойылуы10

2. 2 Негiзгi математикалық моделінің құрастырылуы11

2. 3 Есептеу процедурасының дәлелдеу және сипаттау кезеңдері13

2. 4 Оптималдау есебін сиплекс технологиясы негізінде шешу14

2. 5 Негiзгi аналитикалық модел мен модификация туралы ұсыныстар нәтижелерiн талдау. 16

2. 6 MS EXCEL ортасында «ПОИСК РЕШЕНИЯ» («SOLVER» пакеті) құралы арқылы оптималдық мәнді тексеру18

Қорытынды20

Пайдаланылған әдебиеттер тізімі21

Кіріспе

Кез келген кәсiпорынның, кез келген менеджерлер буындарының негiзгi жұмыстарының бiрі дұрыс шешiм қабылдау болып табылады. Әр түрлi шарттарға байланысты шешiм қабылдау, процесстiң толық негізін түсiну, әр түрлi әдiстер және шешiм қабылдаудың үлгiлерiн қолдану, жұмыстың тиiмдiлiгiнiң жоғарылауындағы түбегейлi рөлдi атқарады.

Сонымен қатар белгілі кәсіпорынның аз ғана шығын жұмсай отырып, максималды көлемде пайда табау жобалары жүзеге асырылып, нарық ағынына қарай өзгертіліп жыл сайын жаңартылып отырады. Оны ғылыми түрде оптималды шешім қабылдау деп атайды. Яғни, оптималды шешім қабылдау арқылы ғана белгілі бір мекеме, кәсіпорындардың көздеген жетістіктеріне жетулеріне мүмкіндіктері бар.

Экономиканың моделдеу әдiстерi соңғы 30 - 40 жылдарда өте екпінді түрде шығарылып отырды. Олар экономикалық мақсаттардың теориялық талдауы үшiн, іс жүзінде жоспарлауда жаттығу мақсаттары үшiн және басқару және болжау үшін құрастырылды. Негізінде экономикалық модель мындай негiзгi процесстердi бiрлестiредi: өндiрiс, жоспарлау, қаражат және басқару т. б. Дегенмен, тиiстi моделдерде кандай болмасын бір процеске тіреу істелінеді (мысалы, жоспарлау процесі), сонда барлық калған процестер ықшамдалған түрде көрiнедi.

Зерттеу мақсаты: Сызықтық бағдарламалаудың әдістері мен моделдері негізінде кәсіпорындарда оптималды шешім қабылдау.

Зерттеу міндеттері:

Берілген есепті іс жүзінде коя білу
Сызықтық бағдарламалау есептiң моделін құру
СБЕ есебін сиплекс әдісімен шешу
Оптималды шешімді қабылдау

Курстық жұмыстың өзектілігі: Операциялық зерттеулердің өткiзілуi, математикалық моделдің құрастырылуы, есептi талдауға және оның оптималды шешiмiн таңдап немесе ұсынылған шешiмдердi дәлелдеуге мүмкiндiк бередi.

Зерттеу пәні: өндiрiстiк - коммерциялық жұмыс үлескен материалды және оған сәйкес қаржылық, ақпараттық ағын.

Зерттеу нысаны: Нарықта кәсіпорындардың оңтайлы, ықшамдалған, оптималды шешімі

Зерттеу әдістері: ашу, іздеу, жүктеу, аудару, талдау, бөлімдерге бөлу, жазу.

I. Сызықтық бағдарламалау әдістері мен модельдері

1. 1 Сызықтық бағдарламалау элеметтері

Күнделікті өмірде қажетті есептердің жобасын жасау және оларды шешу әр түрлі. Дегенмен барлық есептерге ортақ есепті құру және шешу тәсілдерін көрсетуге болады. Жалпы тәжірибиелік есептерді шығару жұмыстарын мынадай кезеңдерге бөледі: есепті қою, есепті формалдау (яғни реттеп-тәртіптеп жазу, керекті мәліметтерді жинау және өңдеу), есептің математикалық моделін құру, есепті шығару әдісін таңдау, есепті күрделі болса, онда оны таңдап алған әдіспен компьютер арқылы шығару үшін программа құру, есепті шығару, есептің шыққан нәтижесін талдау және тәжірибиеде қолдану.

Есептің қойылуы. Қандай есеп құрастырылса да, алдағы мақсаты ашық және толық, түсінікті, нақтылы болуы міндетті түрде қажет. Былайша айтқанда, әр түрлі жағдайларға байланысты не талқыланады? Алға қойған мақсатты орындау үшін қандай мүмкіндіктер бар? Қолда бар қаражат және қорларымыз жете ме? Мақсатты орындауға керекті жағдайларымыз қандай?

Міне осыларға байланысты есептің мақсаты және оны орындауға қажетті шарттар нақтылы сөз жүзінде көрсетіледі. Осы жағдайды есептің сөз жүзінде берілуі (қойылуы) дейді.

Есепті формалдау. Бұл кезең өте жауапты және ауыр қажетті іс-әрекеттерді жасауды қажет етеді. Осы кезеңде есептің математикалық моделі нақтылы, шындыққы жақын болу үшін, есепті шығаруды қажет етіп отырған тұтынушымен, оны математикалық әдіспен шығарушы, яғни орындаушы мамандардың арасында бір-біріне деген толық түсінушілік болуы қажет. Сонымен қатар, есептің сандық математикалық моделін құруға қажетті мәліметтердің сан мәндері толығымен жиналып және олар математикалық-статистикалық әдістермен өңделіп, талдануға тиісті.

Есептің математикалық моделін құру. Алдымен модель деп нені айтатындығына тоқталайық. Қарапайым тұрғыдан қарағанда модель деген әркімге таныс. Мысалы, ойыншық ұшақ - кәдімгі ұшақтың моделі, ойыншық ат - аттың моделі бола алады. Бұл сияқты моделдерді адамдар күнделікті өмірде көп кездестіреді. Күнделікті өмірде аз кездесетін моделдер де бар, ол моделдерді кейбір әр түрлі жағдайда көрсетуге болады. Мәселен, табиғаттың моделін фотосурет түрінде, жоспар түрінде немесе географиялық карта түрінде көрсетуге болады.

Бір затпен екінші немесе үшінші заттардың байланысын математкалық формула түрінде көрсетуге болады, мұны заттардың бір-бірімен өзара байланысын көрсететін математикалық модел дейді. Мсыалы, белгілі формула: S=V*t - материалдық нүктенің бір қалыпты қозғалыс жолының моделі. Есепті сөзбен айтқанда, бір қалыпты қозғалған дене жолының ұзындығы, сол дененің қозғалыс жылдамдығы мен уақытының көбейтіндісіне тең. Сөйтіп, мұндай моделді математикалық модель дейді. Берілген мәліметтерді және есептің шешуінен шығатын қорытындыны матрицалық модель түрінде беру көп жағдайларда талдау жасауларға өте ыңғайлы келеді.

Жоғарыда айтылған ойыншық ат, ұшақ, фотосурет, жоспар, математикалық формула, матрица және тағы басқаларды бір сөзбен айтқанда модель деуге болады. Модельдің қасиеті - оны сол затқа ұқсатуында және заттардың арасындағы заңдылықты толық көрсетуінде (мысалы математикалық, матрицалық т. б) . Модель кейде қарастырып отырған заттың барлық қасиеттерін толық көрсетпеуі мүмкін. Мысалы, ұшақ шығаратын зауыт директорының үстелінде тұрған ұшақ моделі, зауыт шығаратын ұшақтың формасын анық көрсеткенімен, ұшу қабілетіне сәйкес емес. Модель кейде шын затқа ұқсап та, онша ұқсамауы да, қарапайым да, күрделі де болуы мүмкін.

Ғылым мен техниканың өсуіне кибернетика мен электрондық есептеу машиналарының жоспарлау және басқару мәселелеріне кеңінен пайдалануына байланысты кейінгі жылдары экономикалық-математикалық модель деген термин көп қолданылып жүр. Мұны экономикалық үрдістердің математика тілінде жазылуы деп қарастыруға болады. Бұл жағдайларда модельге кірген математикалық символдардың, коэффициенттердің барлығының экономикалық теңеуі (мәні) болуы қажет. Экономикалық-математикалық модельдер формула түрінде де, матрица түрінде де берілуі мүмкін.

Берілген мәліметтердің мазмұнына, есептеу тәсілдері мен қойылу шарттарына байланысты модель статистикалық (егер экономиканың әр түрлі жағдайын қарастырса) және динамикалық (егер экономиканың өсу келешегі қарастырылса) болып бөлінеді. Жоғарыда айтылғандардан, берілген есептің математикалық моделін құру дегеніміз - алға қойған мақсатты және оны орындау үшін қажетті шарттарды математикалық формула түрінде көрсету.

Табылған математикалық модельді шешуге ыңғайлы әдісті таңдап алу керек. Берілген математикалық модельді шешуге көптеген әдістер қолданылуы мүмкін, сөйтіп олардың ішінен тиімді әдісті немесе алгоритмді таңдап алу қажет. Мысалы, сызықтық алгебралық теңдеулер жүйесі үшін Гаусс, Зейдел, кері матрица әдістері, ал оптималды шешімді анықтау үшін симплекс әдістері қолданылады. Осылардың ішінен есептің мақсатына байланысты бір әдісті таңдап алу үрдісі жүзеге асырылады.

1. 2 Сызықтық бағдарламалау есептерінің модельдерінің түрлері және құру жолдары

Экономикалық, техникалық және басқа жоспарлау есептерін құруда теңсіздіктердің маңызы зор. Алгебралық теңсіздіктердің көмегімен көптеген есетердің шарттарын математика тілінде жазуға болады.

Алгебралық теңсіздіктердің тәжірибиелік сызықты ппрограммалау есептерінде қолдану негізін түсіну үшін біраз қарапайым мысалдар қарарастырылады.

1-есеп. Менеджео тігін фабрикасына екі түрлі матадан екі үлгідегі киім тігу жұмысының ұтымды жоспарын құруы керек. Әрбір үлгіде тігілетін киімге матаның екі түрі пайдаланылатын болсын. Әрбір үлгіден бір киім тігуге төменгі кестеде көрсетілгендей әр мата метрі қажет, Бұл көрсеткігтерді экономикалық тілде нормативтік коеффициенттер деп атайды.

Тігілетін киім

1-мата, м

2-мата, м

Тігілетін киім:

1 үлгідегі

2 үлгідегі

1-мата, м:

0, 6

0, 8

2-мата, м:

1, 2

0, 6

Тігін орнында матаның бірінші түрінен 24 метр, екінші түрінен 36 метр болсын. Ал бірінші үлгі бойынша тігілген киімнің бағасы 16 мыы теңге, екінші үлгімен тігілген киімнің бағасы 12 мың теңге болса, қолдағы бар матадан қандай үлгіден тігілгенде ең көп табыс келтіретін жоспар жасау қажет.

Есепті шешу үшін бірінші үлгіден жасалатын киімнің бізге белгісіз саны Х1 ал екінші киімнің санын Х2 деп алайық. Бұл белгілеу бойынша тігілген киімдерден түсетін жалпы табысты былай өрнектеуге болады:

Z=16X1+12X2 max;

Мұндағы 16Х1 - бірінші үлгідегі киімнен түсетін табыс. 12Х2 - екінші үлгідегі киімнен түсетін табыс, ал Z екі үлгідегі киімнен түсетін жалпы табысты көрсетеді. Есептің шарты бойынша Z ең көп табыс болу керек, сондықтан ең көп (ең үлкен) дегенді максимум немесе қысқаша математика тілінде MAX деп белгілеуге болады.

Енді есептің шарттарын жазайық. Бірінші матадан бірінші үлгідегі киімнің бір данасына 0, 6 м керек болса, Х1 данасына 0, 6Х1 болар еді, ал осы матадан екінші үлгідегі бар дана киімді жасау үшін 0, 8 м керек болса, Х2 данасына 0, 8Х2 қажет. Екі үлгідегі киімге жұмсалатын матаның қолда бары 24 метрден артпауы керек. Ендеше бірінші мата үшін мына теңсіздік орындалады:

0, 6Х1+0, 8Х2≤24;

Екінші мата теңсіздігі келесі түрде болады:

1, 2Х1+0, 6Х2≤36;

Алгебралық теңсіздіктерді шешкенде Х1 мен Х2 мәндері теріс сандар да болуы мүмкін. Ал қарастырылып отырған есепте Х1 мен Х2-нің мәндері тек оң сан немесе нөл болуға тиіс. Белгісіздердің мәндері оң сан болса, онда белгіленген үлгілі киім тігіледі, ал нөлге тең болса, онда ол киім тігілмейді дегенді білдіреді. Белгісіздің мәні теріс болуы мүмкін емес. Онда жоғарғы шарттармен қоса есепке мынадай шарттар қосу қажет: Х1≥0, Х2≥0;

Есепте қойылған шарттарды математикалық түрде былай өрнектеуге болады:

Z=16X1+12X2 max

0. 6X1+0. 8X2≤24

1. 2X1+0. 6X2≤36

X1≥0, X2≥0;

1. 3 Симплекс әдісінің негіздері

Жалпы математикалық бағдарламалау пәні өмірдің қажеттілігінен пайда болған қолданбалы математиканың ең негізгі бөлімі. Жоғарыда айтылғандай математикалық бағдарламалаудың ішіндегі барлық халық шаруашылығына көп таралғаны, әртүрлі әдістері терең зерттелген бөлімі сызықтық бағдарламалау әдістері болып есептелінеді. Математикалық бағдарламалау пәнінің ең негізгі бөлімі сызықтық бағдарламалау есептері дүние жүзінде ең бірінші рет 1930 жылдары жарық көрді. Сызықтық бағдарламалау есептері басқа тәжірибиелік есептерге қарағанда өте қарапайым, зерттеуге ыңғайлы.

Сызықтық бағдарламалау есебін шешудің кең тараған түрлерінің бірі болып симплекс әдісі табылады. Симплекс әдісінің геометриялық мағынасы болып: Сызықтық бағдарламалау есебінің оптималды шешімін табу болып табылады. Симплекс ағылшынның (Кеңістіктегі қарапайым көп бұрыштың немесе көп жақты бейненің түсінігі) ретінде беріледі. Оның бұрыштарының координаттары ізделініп отырған белгісіздердің оптималды мәндеріне сәйкес. Симплекс әдісінің негізгі мақсаты - егер мақсат функция максимумға ізделінсе онда алғашқы төбеден келесі төбеге жылжығанда оптималды шешімді табуды қамтамасыз ету. Егер есеп оптмалдауға ізделінсе онда алғашқы мақсат функцияның мәнінен кейінгі мәні кіші болуын қамтамасыз ету. Симплекс әдісі арқылы бір төбеден келесі төбеге көшкенде белгілі бір бағытта жоспарлы түрде көшіріледі. Симплекс әдісі бір мүмкін шешімнен келесі мүмкін шешімге өтуді жүзеге асырады. Нәтижесінде мақсат функция өседі немесе кемиді. Оптималды шешім белгілі бір қадамдар жүргізілгеннен кейін табылады. Симплекс әдісін 1947 жылы неміс ғалымы Г. Даицинг шығарған. Симплекс әдісін басқаша жоспарды тізбектей жақсарту әдісі деп те атайды.

Симплекс әдісінің мақсаты мен идеясын толық түсіну үшін есепті жалпы түрде қарастырып, әдісті тәжірибелік есептерге қолдану жолы қарастырылады. Ол үшін ең алдымен сызықтық бағдарламалау есептерінің жалпы моделінің мәнісіне тоқталынады. Сызықты бағдарламалаудың негiзгi есебі төмендегiше тұрғызылады: қатар айнымалы болады 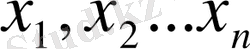. Мұндай сызықты теңдеулердiң жүйесiне қанағаттандыратын олардың терiс емес мәндерiн табу керек болады:

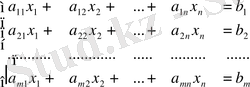(1. 1)

және бұдан басқа, сызықты мақсаттық функцияны минимумға айналдыру

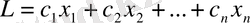
Мақсаттық функция аударуы керек болған жағдай минимум емес, егер функцияның таңбасын өзгертсе және функцияның орынына қарап шықса максимумға ұмтылатыны анық

Ұйғарымды шешiм деп 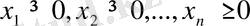жеткiлiктi жиынтықты айнымалыны атайды (1. 1) .

Ұтымды шешiммен мақсаттық функцияның жанында минимумға айналған деп атайды.

Сызықты бағдарламалау есептеріндегі шектеулерi iс жүзiнде жиi теңдеулер емес, теңсiздiк түрінде берiлген. Сызықты бағдарламалауда негiзгi есепке осы жағдайда өтуге болады.

Шектеулермен болатын сызықты бағдарламалаудың есептерін қарап шығамыз, олар мына түрде болады

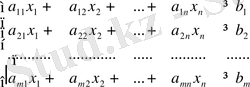(1. 2)

және сызықты - тәуелсiз болып табылады. Соңғысы ешқандай да олардың iшiнен сызықты комбинацияның басқа түрiнде көрсетуге болмайтынын бiлдiредi. Теңсiздiктерге қанағаттандыратын және минимумдарға айналдыратын 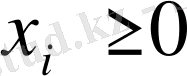табу керек болады

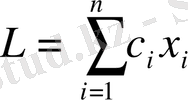
Теңдеу енгiземiз

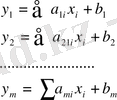: (1. 3)

Онда 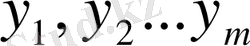- қосымша айнымалылар, сол сияқты 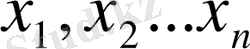терiс емес болып табылады.

Сайып келгенде, сызықты бағдарламалаудың ортақ есебін аламыз - 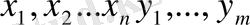, терiс емес табу, олар (1. 2. 3 ) теңдеулердiң жүйелерiне қанағаттандыру үшiн минимумдарға айналдыру

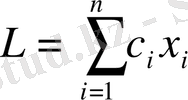
II. Сызықтық бағдарламалау есептерін шешу

2. 1 Тәжірибиелік операциядағы есептің қойылуы

«Флора» мен «Росток» тыңайтқыштарын шығарғанда кәсіпорын мынадай 3 түрлі шикізатты қолданады: азот қышқылы, амиак және калий тұзы. Әрбір 1 т тыңайтқышты шығаруға кететін шикізат көлемі, шикізат қоры және әрбір 1 т тыңайтқыштарды сатумен түскен пайда төмендегі кестеде көрсетілген:

Шикізат түрлері: Шикізат түрлері

Қор (т): Қор (т)

1 т тыңайтқышқа кететін шикізат шығыны (т): 1 т тыңайтқышқа кететін шикізат шығыны (т)

Шикізат түрлері: "Флора"

Қор (т): "Росток"

Шикізат түрлері:

Азот қышқылы

Аммиак

Калий тұзы

Қор (т):

900

1000

800

1 т тыңайтқышқа кететін шикізат шығыны (т):

2, 5

Шикізат түрлері: Түскен пайда

Қор (т): 5

1 т тыңайтқышқа кететін шикізат шығыны (т): 8

2. 2 Негiзгi математикалық моделінің құрастырылуы

Берілген есептің математикалық моделін құру үшін Х1 және Х2 айнымалыларын енгіземіз және олардың көмегімен мақсат функция мен шектеулер жүйесін құрамыз.

X1−шығарылатын шикізат көлемі «Флора» (тонна) ;

Х2−шығарылатын шикізат көлемі «Росток» (тонна) ;

Есептiң шартын есепке алатын шектеулердi құрамыз. Азот қышқылының шығынына шектеудi құраймыз. 1 т «Флора» тыңайтқышын шығару үшін 1 т азот қышқылы жұмсалады. Яғни, флораның барлық көлемін шығаруға жұмсалатын азот қышқылының көлемі Х1 тонна «Расток» тыңайтқышын шығаруға 4Х2 тонна азот қышқылы жұмсалатын болады. Сонымен, жұмсалатын азот қышқылының көлемін былай жазуга болады:

X1 + 4X2т. Мұнда азот қышқылының көлемі 900 т аспауы керек, себебі азот қышқылының қордағы көлемі тек 900 т құрайды. Сол себепті келесі шектеуді белгілейміз:

X1+4X2 ≤ 900;

Сол сияқты амиакқада шектеу құрауға болады:

2, 5X1+2X2≤ 1000;

Және калий тұзын жұсамға шектеу;

3Х1+2Х2≤800;

Бұдан басқа, X1 және X2 айнымалылары өз беттерiнше терiс мәндер қабылдай алмайды, өйткені оларда тыңайтқыштардың тонна бойынша сандары берілген. Сондықтан тыңайтқыштар саны теріс сан болмауы үшін шектеу көрсету керек:

X1>0, X2>0;

Берілген есепте шығарылатын тыңайтқыштар тонналарының санын анықтау және оларды өндіргенде кәсіпорын максимал пайда табатындай етіп шығару керек. 1 тонна «Флора» тыңайтқышын шығарғанда кәсіпорынға 5 тг пайда түседі. Ал барлық «Флора» тыңайтқышын шығарғанда 5Х1 тг. «Росток» тыңайтқышын шығарғандағы кіріс көлемі 8Х2 құрайды. Сонымен тыңайтқыштарды шығару арқылы түскен жалпы кіріс көлемі 5Х1+8Х2. Келесі кезекте кәсіпорынға түсетін кіріс көлемі максимал болатындай Х1 және Х2 мәндерін табу керек.

Сондықтан, осы есеп үшiн мақсаттық функция келесi түрде болады:

Е = 5X1 + 8X2 →max

Бұл функцияны симплекс әдісімен шешу үшін оны стандартты формаға келтіру қажет. Барлық «<, >, =» шектеулерін міндетті түрде «=»-ге ауыстыру керек. Ол үшiн әрбiр шектеуге (қалдық ) қосымша айнымалы қосу керек болады. Стандартты формадағы есептiң математикалық модельі келесi түрде болады:

Х1+4Х2+Х3=900

2, 5Х1+2Х2+Х4=1000

3Х1+2Х2+Х5=800

Е = 5X1 + 8X2 →max

X1>0, X2>0.

Х3 - азот қышқылының қалдығы;

Х4 - аммиак қалдығы;

Х5 - калий тұзының қалдығы.

2. 3 Есептеу процедурасының дәлелдеу және сипаттау кезеңдері

Пайданы максималды түрде тауып «Флора» мен «Росток» тыңайтқыштарының шығарылымының ұтымды көлемiн анықтайтындай етіп, берілген есепті шығару керек. Есептiң математикалық моделін құру арқылы мақсат функция мен шектеулер сызықты екеніне көз жеткіздік. Онда бұл есеп сызықтық бағдарламалау есептеріне жатқызылады. Берілген математикалық моделін шешу үшін сызықтық бағдарламалаудың көптеген әдістер қолданылуы мүмкін. Солардың ішінен ең тиімді, ыңғайлы Симплекс әдісі таңдалынды.

Сызықтық бағдарламалау есептерін шешудің кең тараған тәсілдерінің бірі болып симплекс әдісі болып табылады. Симплекс әдісінің геометриялық мағынасыболып: Сызықтық бағдарламалау есептерінің оптималды шешімін табу. Симплекс ағылшынның кеңістіктегі қарапайым көп бұрыштың немесе көп жақты бейненің түсінігі ретінде беріледі. Оның бұрыштарының координаттары, ізделініп отырған белгісіздердің оптималды мәндеріне сәйкес. Симплекс әдісінің негізгі мақсаты - егер мақсат функция максимумға ізделінсе, онда алғашқы төбеден келесі төбеге жылжығанда оптималды шешімді табуды қамтамасыз ету. Сонымен, симплекс әдісін қолданғанда бір төбеден келесі төбеге көшкенде белгілі бір бағытта жоспарлы түрде көшіледі, бұл жағдайда кейбір «керексіз» көпжақтының төбелері қарастырылмай қалып қалады да, есептің шешу жұмысы ұтымды, жылдам жүргізіледі.

2. 4 Оптималдау есебін сиплекс технологиясы негізінде шешу

Шығарылатын есептiң математикалық моделі келесi түрде болады:

Х1+4Х2+Х3=900

2, 5Х1+2Х2+Х4=1000

3Х1+2Х2+Х5=800

Е = 5X1 + 8X2 →max

X1>0, X2>0.

Бастапқы симплекс кестесі құрастырылады (кесте. 1) :

Кесте 1.

Базис: Базис

Х1: Х1

Х2: Х2

Х3: Х3

Х4: Х4

Х5: Х5

Решение: Решение

Базис: E

Х1: -5

Х2: -8

Х3: 0

Х4: 0

Х5: 0

Решение: 0

Базис: Х3

Х1: 1

Х2: 4

Х3: 1

Х4: 0

Х5: 0

Решение: 900

Базис: Х4

Х1: 2, 5

Х2: 2

Х3: 0

Х4: 1

Х5: 0

Решение: 1000

Базис: Х5

Х1: 3

Х2: 2

Х3: 0

Х4: 0

Х5: 1

Решение: 800

Базистік айнымалы анықталынады.

Х2 айнымалысының қатарыннан базистік айнымалы анықталады. Өйткенi оған E жолының модул бойынша максимал терiс коэффициентi (-8) мәні сәйкес келедi. Бұл «Росток» тыңайтқышының шығарылымының үлкеюiн бiлдiредi. Есеп және мақсаттық функцияның шарттарынан «Росток» тыңайтқышының шығарылымының үлкеюi, «Флора» тыңайтқышының шығарылымының үлкеюіне қарағанда, мақсат функцияны жылдамырақ өсіріп алып келгенiн көруге болады: «Росток» тыңайтқышының әрбiр тоннасының шығарылымынан мақсат функция 8 тенгеге үлкейсе. Ал флораның әрбiр тоннасынан мақсат функция тек 5 тенгеге үлкейеді.

Базистен шығару үшiн айнымалы анықталады. Ол үшiн шешiм бағанасының коэффициенттерiн Х2 бастаушы бағананың коэффициенттерiне бөлуге керек. (сонымен бiрге бастаушы бағананың коэффициенттерi оң сан болуы керек) . Нәтижесінде симплекстік қатынас шығады:

900/4=225; 1000/2=500; 800/2=400.

Базистен шығарылып тасталынатын айнымалыны iздестiрудің мәні мынада: кестеге жаңа базистікайнымалыны қосқанда, оның мәнi үлкейедi. Сонымен бірге есептiң бастапқы шектеулерiн сақтап отыру үшін, базистiк айнымалыларды азайтып отыру қажет. Айнымалыларды тек 0-ге дейін ғана азайтуға болады. Симплекс қатынасы базиске енетін айнымалылардың қанша үлкеюлерінен кейін, базистік айнымалы 0-ге жақындайтынын көрсетеді. Сондықтан ең төменгi симплекстік қатынас көрсететін айнымалы базистен шығарылады. Базистен алынып тасталынатын жол мен айнымалы басқару жолы деп аталады. Сонымен, базистік айнымалыдан Х3-ті алып тастаймыз, (симплекстік қатынасының мәні 225) және Х3 жолы бастауыш болып табылады. Х3 басқару жолымен Х2 басқару бағанының қиылысқан жерінде орналасқан элемент, басқару элементі деп аталады. Берілген кесте үшінбасқару элементі 4-ке тең.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.