Тригонометриялық теңсіздіктерді шешу әдістері мен дәлелдері


МАЗМҰНЫ
Кіріспе . . . 3
- Тригонометриялық теңсіздіктер . . . 5
- Тригонометриялық теңсіздіктерді шешу әдістері . . . 7тригонометриялық формулаларды қолдану әдісі . . . 7Бірлік шеңбер әдісі . . . 9Графиктік әдіс . . . 19
- Теңсіздіктерді дәлелдеу . . . 22
- Шартты теңсіздікті дәлелдеу . . . 24
Қорытынды . . . 29
Әдебиеттер тізімі . . . 30
- Кіріспе
Тригонометрияның тарихы жөнінде. «Тригонометрия» сөзі алғаш рет (1505 ж. ) неміс геологы және математигі Питискустың кітабының мазмұнында кездеседі. Бұл сөз грек тілінен алынган: ұшбүрыш, өлшеуіш. Басқаша сөзбен айтқанда, тригонометрия - ұшбұрыштарды өлшеу жөніндегі ғылым. Атауы біршама кейінірек шыққанмен, тригонометрияға қатысты казіргі ұғымдар мен фактілер бұдан екі мың жыл бұрын белгілі болған.
Синус ұғымының тарихы әріден басталады. Фактіге жүгінсек, ұшбұрыш пен шеңбер кесінділерінің арасындағы әр түрлі қатыстар (шын мәнінде тригонометриялык функциялардың да) біздің заманымызға дейінгі III ғасырда өмір сүрген Грецияның ұлы математиктері -- Евклидтің, Архи-медтің, Аполлоний Пергскийдің еңбектерінде кездеседі. Бұл қатыстарды римдік кезеңде, арнайы атауға ие болмағанмен, М е н е л а й (б. з. I ғ. ) барынша жүйелі зерттеген еді. Қазіргі күнде а бұрышының синусы, мысалы, шамасы а-га тең центрлік бұрышқа тірелетін жарты хорда ретінде немесе екі еселенген доғаның хордасы ретінде зерттелді. Косинус сөзі одан көп кейін пайда болды.
Косинус - латынның «толықтауыш синус» (немесе, басқаша айтканда, «толықтауыш доғаның синусы») деген сөз тіркесінің қысқарған түрі.
Біз тригонометриялық функциялармен жүмыс істегенде «ұшбұрыш өлшеу» такырыбына берілген есептер шеңберінен шығып кетеміз. Сондықтан белгілі математик Ф. К л е й н (1849-1925) «тригонометриялық» функциялар туралы ілімді басқаша - гониометрия деп атауды ұсынған (латынша «бұрыш» дегенді білдіреді) . Алайда бұл атау қабылданбаған.
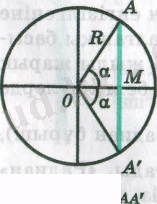
Тангенстер көлеңкелердің ұзындықтарын анықтау жөніндегі есептерді шығаруға байланысты пайда болды. Тангенс (сондай-ақ котангенс, секанс жене косеканс) атауын X ғасырда араб математигі Абу-л-Вафа енгізген, ол тангенстер мен котангенстерді табуға арналған кестелерді де түңғыш рет жасады.
Тригонометриялық теңсіздіктерді шешу-сандық теңсіздіктерді, сандық теңсіздіктер жүйелерін шешу сияқты маңызды тақырыптармен тең келеді.
Тригонометриялық теңсіздіктер мен теңдеулерге мектеп курсынан ақ ерекше орын болінуі тарихи қалыптасқан жағдай. Тіптен ежелгі гректер тригонометрияны маңызды ғылым деп санаған себебі геометрия - математика патшасы, ал тригонометрия - геометрияның патшасы. Сондықтан біз де ежелгі гректерге қарсы шықпай, тригонометрияны - мектеп курсыныңі және де математика ғылымың маңызды бөлімі деп есептейік.
Мектеп курсында тригонометриялық теңсіздіктерді шешу неден басталады? Әрине тригонометриялық функциялардың өздерінен. Ен әуелі sin x, cos x, tg x және ctg x қатынастары өзі беріледі. Бұл қарастырылып отырған ұшбұрыштар мысалында беріледі.
- 1. Тригонометриялық теңсізідіктер
Тригонометриялық теңсіздіктерді шешу үшін бірнеше маңызды кезеңдерден өту керек.
- sin x, cos x, tg x и ctg x ұғымдарын енгізу. Радиусы 1-ге тең, центрі координаталар басында жататын шеңбердібірлік шеңбердеп атайды. Бірлік шеңбердіңРанүктесі Р0(1; 0) нүктесін а радианға тең бұрышқа бұрғанда шыққан болсын. Ранүктесінің координатасы - а бұрышының косинусы екенін аңғару қиын емес
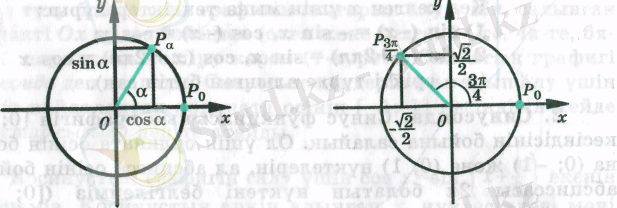
Анықтама. у = sin х және у = cos х формулаларымен берілген сандық функцияларды сәйкесінше синус және косинус деп атайды
Анықтама. у = tg х және у = ctg х формулаларымен берілген сандық функцияларды сәйкесінше тангенс және котангенс деп атайды
- келесі қадам функцияларды енгіземіз y = sin x, y = cos x, y = tg x и y = ctg x. Бұл кезеңде осы функциялардың қасиетері, анықталу облысы мен мәндер облысы қарастырылып өтеді, ал ең маңызды - графиктерімен танысу.
- Және тригонометриялық теңсіздіктерді шешуге дайындыққа ең соңғы кезең. Бұл кезеңде оқушылар маңызды тригонометрия формулаларымен және оларды қалай қолдану керек екендігімен танысады. Бұл кезеңде алынған біліммен оқушылар бүкіл математика курсында колдана алады. Меңгерілген формулалар көмегімен өте қиын, көлемді тригонометриялық теңдеулер мен теңсіздіктерді жеңіл шешуге болады.
Енді, оқушылар бастапқы кезеңдерді жақсы меңгеріп, біздің тақырыбымызға жетеді, яғни тригонометриялық теңсіздіктерге. Әрине теңсіздіктерді шешу қарапайымдардан басталады sin x > a, sin x < a; cos x > a, cos x < a; tg x > a, tg x < a. Осы теңсіздіктерді меңгергеннен кейін қиындығы жоғары теңсіздіктерге келеді, бұнда әр түрлі дәрежелі күрделі функциялар. Әрине 16-17 жастағы балалар үшін мұндай материалды меңгеруді жеңіл деп айта алмайсын. Ол абстракті ойлауды, мидың аналитикалық қалыптсуы және ең маңыздысы ойлаудың шапшаңдығын қажет етеді. Сол себептен бұндай күрделі материалды меңгеруге қосымша методикалар қажет. Бағымызға орай мұндай қарапайым тригонометриялық теңсіздіктерді шешудің жеңіл тәсілдері табылды. Олар бір емес екі.
Бұл жерде зейінді оқырман келесі сұрақ қойуы мүмкін. Қарапайым теңсіздіктерді шешуге арнайы әдіс тәсілдердің ойластырылуының қажеті не егер қарапайым теңсіздіктер онсыз да өзі шешіліп тұрса. Бірақ бұған жауап беруге болады, кез - келген тригонометриялық теңсіздік, сырттан қарағанда ауқымды және күрделі болып көрінсе де оларға негізгі тригонометриялық түрлендірулерді қолданып қарапайым түрге келтіруге болады. Түрлендіргеннен кейін теңсіздікті тригонометриялық шеңбер арқылы немесе функцияның графигі арқылы шешеміз.
Негізінде мектеп курсында тригонометриялық теңдеулерді шешуде қандай әдісті қолдану тиімді екендігі жөнінде нақты нұсқаулар жоқ. Бұл жерде таңдау тек мұғалімдердің өз қалауларына байланысты болады. Менің ойымша тригонометриялық шеңберді қолдану тиімдірек болады. Себебі бұл өте көрнекі тәсіл және дәптерде аз орын алады. Негізі қарапайым тригонометриялық теңсіздіктерді шығарған кезде уақыт мүмкіндік беріп жатса екі тәсілді де қолданған жөн. Сонымен айтып кеткенімдей тригонометриялық теңсіздіктеріне тригонометриялық түрлендірулер қолданып оны қарапайым түрге келтіргеннен кейін тригонометриялық шеңбер немесе графикалық әдісті қолданамыз.
2. Тригонометриялық теңсіздіктерді шешу әдістері
2. 1 Тригонометриялық формулаларды қолдану әдісі
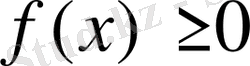 түріндегі қүрделі тригонометриялық теңсіздіктерді шешкенде оларға тригонометриялық түрлендіру формулаларын қолданып оны қарапайым түрге келтіріп алуға болады. Бұған келесі формулалар қолданылады
түріндегі қүрделі тригонометриялық теңсіздіктерді шешкенде оларға тригонометриялық түрлендіру формулаларын қолданып оны қарапайым түрге келтіріп алуға болады. Бұған келесі формулалар қолданылады
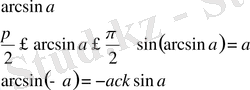
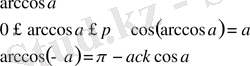
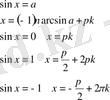
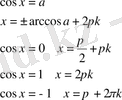
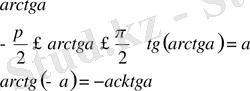
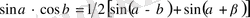
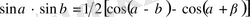
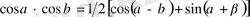
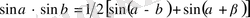
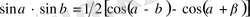
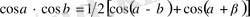
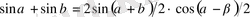
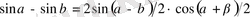
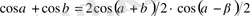
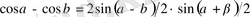
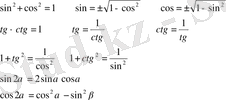
- 2. 2 Бірлік щеңбер арқылы тригонометриялық теңсіздіктерді шешу
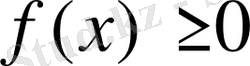 түріндегі тригонометриялық теңсіздіктерді шешкенде, бұл жерде
түріндегі тригонометриялық теңсіздіктерді шешкенде, бұл жерде
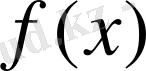 - тригоноометриялық функциялардың бірі, тригонометриялық шеңберді теңсіздікті көрнекі түрде шығарып жауабын жазып алуда қолданған қолайлы
- тригоноометриялық функциялардың бірі, тригонометриялық шеңберді теңсіздікті көрнекі түрде шығарып жауабын жазып алуда қолданған қолайлы
Есеп шешудің алгоритмі:
- бірлік шеңбер сызамыз
- t-ның берілген теңсіздікті қанағатандыратын мәндерінде бірлік шеңбердің барлықнүктелерінің ординаталарыадан үлкен немесе оған тең және кіші немесе оған тең болады.
- қарай берілген функцияға байланысты - сағат тілінің қозғалысын анықтаймыз
- ендіментабамыз данеанықтаймыз
- Ұзындығыге тең пайда аралықтағы теңсіздіктің шешімдерін табамыз.
 ,
,
 ,
,
 ,
,
 түріндегі теңсіздіктерді шешу
түріндегі теңсіздіктерді шешу


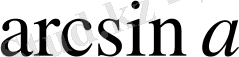
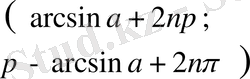



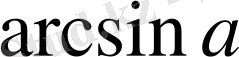
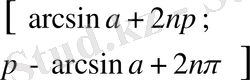


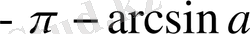
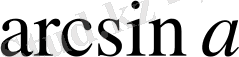
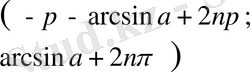


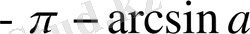
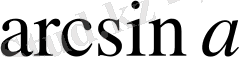
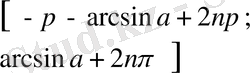

 ,
,
 ,
,
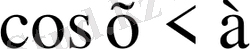 ,
,
 түріндегі теңсіздіктерді шешу
түріндегі теңсіздіктерді шешу



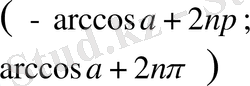




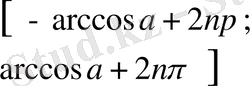

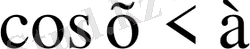

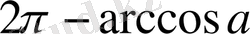
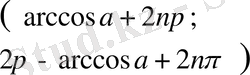



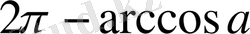
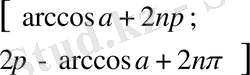

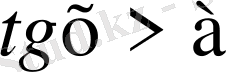 ,
,
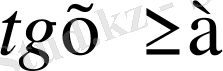 ,
,
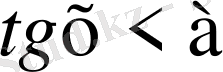 ,
,
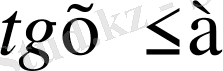 түріндегі теңсіздіктерді шешу
түріндегі теңсіздіктерді шешу
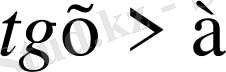
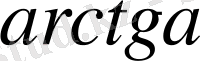
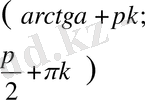
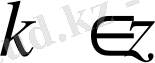
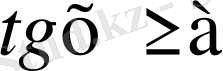
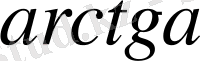
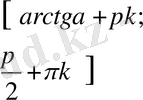
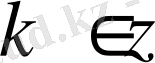
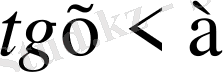
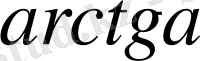
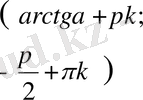
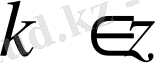
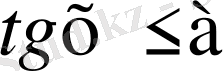
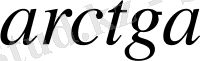
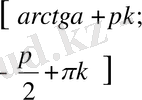
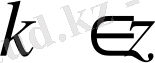
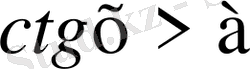 ,
,
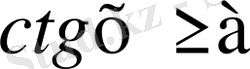 ,
,
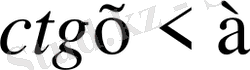 ,
,
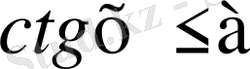 түріндегі теңсіздіктерді шешу
түріндегі теңсіздіктерді шешу
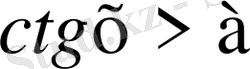
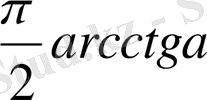
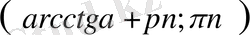

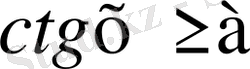
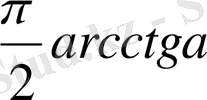
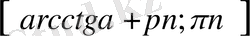

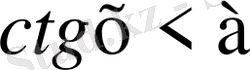
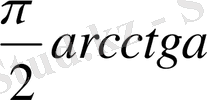
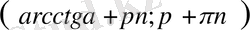

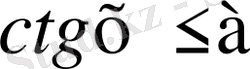
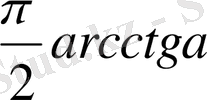
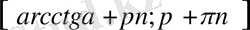

Мысал - 1
теңсіздікті шешіңіз
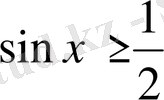 .
.
Шешуі.
Тригонометриялық шеңбер сызып бойында нүктелерді белгілейік. Ордината
 аспайтын.
аспайтын.
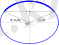
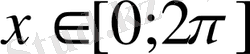 үшін бұл теңсіздіктің шешімі
үшін бұл теңсіздіктің шешімі
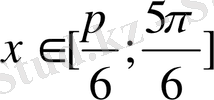 . Және тағы егер кез келген х саны берілген интервалдан
. Және тағы егер кез келген х саны берілген интервалдан
 айырмашылық болса, онда
айырмашылық болса, онда
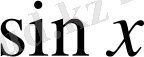 те
те
 кіші болады. Яғни табылған кесіндінің соңына жай ғана
кіші болады. Яғни табылған кесіндінің соңына жай ғана
 қосу керек.
қосу керек.
жауабы.
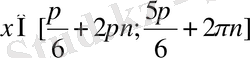 .
.
Мысал - 2
теңсіздікті шешейік .
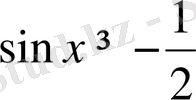
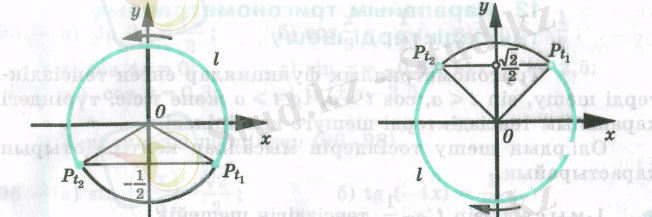
t-
ның берілген теңсіздікті қанағатандыратын мәндерінде бірлік шеңбердің барлық
 нүктелерінің ординаталары
нүктелерінің ординаталары
 - ден үлкен немесе оған тең болады. Осындай нүктелердің жиыны -
- ден үлкен немесе оған тең болады. Осындай нүктелердің жиыны -
 доғасы, ол суретте қалың кара сызықпен көрсетілген.
доғасы, ол суретте қалың кара сызықпен көрсетілген.
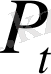 нүктелерінің осы доғада жату шартын табайық.
нүктелерінің осы доғада жату шартын табайық.
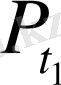 нүктесі оң жақ жартышеңбердің бойында жатады және ординатасы
нүктесі оң жақ жартышеңбердің бойында жатады және ординатасы
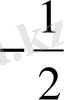 -ге тең, олай болса,
-ге тең, олай болса,
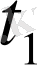 ретінде
ретінде
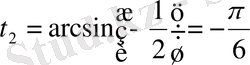
мәнін алған ыңғайлы. Біз
 доғасын
доғасын
 нүктесінен
нүктесінен
 нүктесіне қарай сағат тілінің қозғалысына қарсы бағытта жүріп өтеміз деп елестетейік. Сонда
нүктесіне қарай сағат тілінің қозғалысына қарсы бағытта жүріп өтеміз деп елестетейік. Сонда
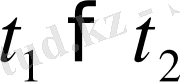 және
және
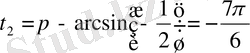 - болатынын түсіну оңай. Сонымен, егер
- болатынын түсіну оңай. Сонымен, егер
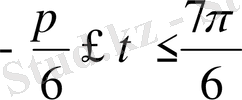 болса,
болса,
 нүктесі
нүктесі
 доғасында жатады. Сөйтіп, үзындығы
доғасында жатады. Сөйтіп, үзындығы
 ге тең
ге тең
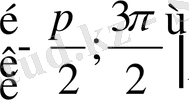 аралығына тиісті теңсіздіктердің шешшдері
аралығына тиісті теңсіздіктердің шешшдері
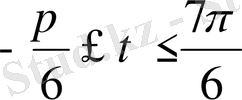 болады. Синус периодты функция екенін ескеріп, табылған шешімге периодын қосып, қалған шешімдерін ала-мыз. Сонымен жауабы мынадай болады:
болады. Синус периодты функция екенін ескеріп, табылған шешімге периодын қосып, қалған шешімдерін ала-мыз. Сонымен жауабы мынадай болады:
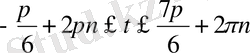
Мысал 2:
теңсіздікті шешіңіз .
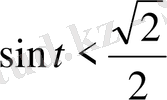
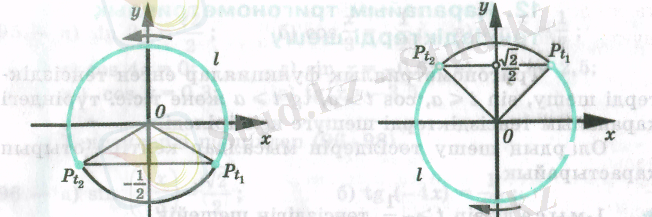
Бұл теңсіздік бірлік шеңбердің барлық
 нүктелерінің
t
-
ның берілген теңсіздікті қанағаттандыратын мәндерінде ординатасы
нүктелерінің
t
-
ның берілген теңсіздікті қанағаттандыратын мәндерінде ординатасы
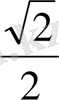 ден кіші болатынын білдіреді. Осындай барлық нүктелердің жыны
ден кіші болатынын білдіреді. Осындай барлық нүктелердің жыны
 доғасы, суретте жуан қара сызықпен көрсетілген. Доғаның ұштары
доғасы, суретте жуан қара сызықпен көрсетілген. Доғаның ұштары
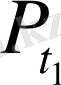 және
және
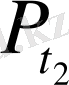 қарастырып отырған жиынға енбейді, өйткені олардың ординаталарыден
қарастырып отырған жиынға енбейді, өйткені олардың ординаталарыден
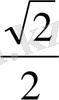 кіші емес, оған тең.
кіші емес, оған тең.
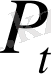 Нүктесінің көрсетілген жиынға тиістілік шартын анықтау үшін
Нүктесінің көрсетілген жиынға тиістілік шартын анықтау үшін
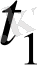 мен
мен
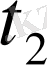 табамыз.
табамыз.
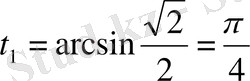 Деп аламыз.
Деп аламыз.
 доғасының бойымен
доғасының бойымен
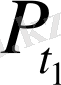 нүктесінен
нүктесінен
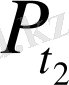 нүктесіне қарай сағат тілінің қозғалыс бағытымен жүруді қарастырайық
нүктесіне қарай сағат тілінің қозғалыс бағытымен жүруді қарастырайық
 және
және
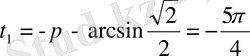 . Ұзындығы
. Ұзындығы
 ге тең
ге тең
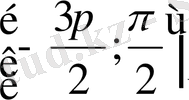 аралығындағы теңсіздіктің шешімдері
аралығындағы теңсіздіктің шешімдері
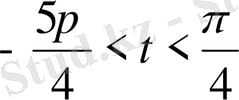 болады. Синус периодты болғандықтан, теңсіздіктің барлық шешімдері:
болады. Синус периодты болғандықтан, теңсіздіктің барлық шешімдері:
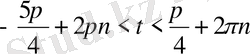
Мысал3:
теңсіздікті шешіңіз .
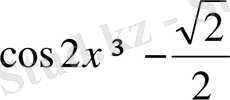
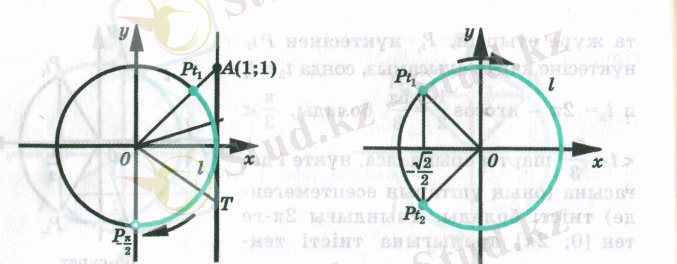
2х-ті t арқылы белгілесек, теңсіздік
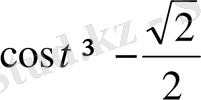 түріне келеді. суретте осы теңсіздікке сәйкес келетін
түріне келеді. суретте осы теңсіздікке сәйкес келетін
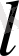 доғасы жуан қара сызықпен көрсетілген.
доғасы жуан қара сызықпен көрсетілген.
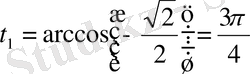 болатынын табамыз, бұдан
болатынын табамыз, бұдан
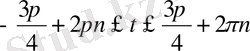 .
Белгілеудегі t ның орнына 2х ті апарып қойсақ
.
Белгілеудегі t ның орнына 2х ті апарып қойсақ
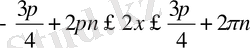 ;
;
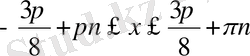
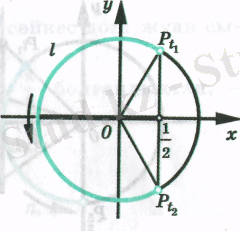 Мысал4:
теңсіздікті шешіңіз .
Мысал4:
теңсіздікті шешіңіз .
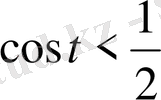
Абциссалары
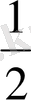 ден кіші болатын бірлік шеңбер нүктелерінің жиыны
ден кіші болатын бірлік шеңбер нүктелерінің жиыны
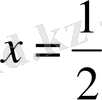 түзудің сол жағында жатады. Суретте жуан қара сызықпен көрсетілген
түзудің сол жағында жатады. Суретте жуан қара сызықпен көрсетілген
 доғасы. Доғаның ұштары
доғасы. Доғаның ұштары
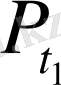 және
және
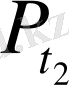 қарастырып отырған жиынға енбейді.
қарастырып отырған жиынға енбейді.
 мен
мен
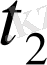 табамыз. Нүктесі жоғарғы шарты шеңберде жатады, абциссасы
табамыз. Нүктесі жоғарғы шарты шеңберде жатады, абциссасы
 ге тең сондықтан
ге тең сондықтан
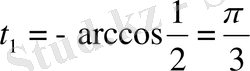
 доғасының бойымен сағат тілінің қозғалысына қарама-қарсы бағытта жүре отырып,
доғасының бойымен сағат тілінің қозғалысына қарама-қарсы бағытта жүре отырып,
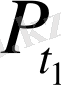 нүктесінен
нүктесінен
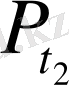 нүктесіне қарай ауысамыз, сонда
нүктесіне қарай ауысамыз, сонда
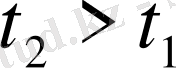
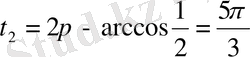 болады.
болады.
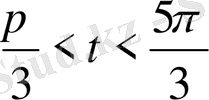 шарты орындалса,
шарты орындалса,
 нүкте доғасына тиісті болады. Ұзынды
нүкте доғасына тиісті болады. Ұзынды
 -ге тең
-ге тең
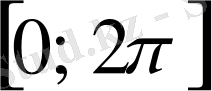 аралығына тиісті теңсіздіктердің шешімдері:
аралығына тиісті теңсіздіктердің шешімдері:
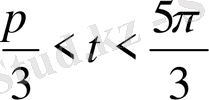 . Косинустың периодты екенін ескеріп, теңсіздіктің шешімдер жиынын мына түрде жазамыз
. Косинустың периодты екенін ескеріп, теңсіздіктің шешімдер жиынын мына түрде жазамыз
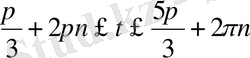 .
.
Мысал5:
теңсіздікті шешіңіз
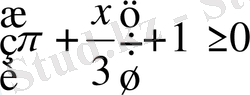 .
.
Шешуі. .
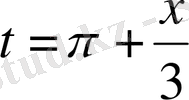 деп белгіліейік, онда теңсіздік қарапайым түрге келеді:
деп белгіліейік, онда теңсіздік қарапайым түрге келеді:
 . Тангенстің ең кіші оң периодты ұзындығына тең интервалды қарастырайық
. Тангенстің ең кіші оң периодты ұзындығына тең интервалды қарастырайық
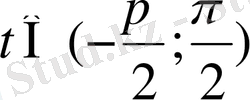 . Осы кесіндіде
. Осы кесіндіде
тангенстер сызығының көмегімен
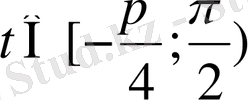 орнатамыз. Енді есімізге
орнатамыз. Енді есімізге
 қосу керек екенін түсіріміз, өйткені
қосу керек екенін түсіріміз, өйткені
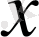
 . Сонымен,
. Сонымен,
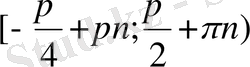 .
.
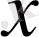 айнымалысына оралсақ, келесіні аламыз
айнымалысына оралсақ, келесіні аламыз
 .
.
Жауабы.
.
- Тригонометриялық теңсіздіктерді графиктік әдіспен шешу
Есеп шешудің алгоритмі:
- функциясының графигін саламыз.
- осінде, берілген аралыққа сәйкес келетін х мәнін таңдаймыз
Байқауымызша егер
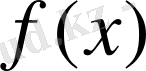 --- периодтық функция болса, онда
--- периодтық функция болса, онда
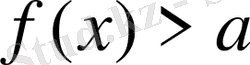
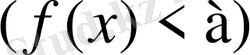 теңсіздіктерінің шешімін
теңсіздіктерінің шешімін
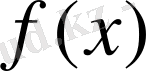 функциясының периодының ұзындығына тең кесіндіден іздеу керек.
функциясының периодының ұзындығына тең кесіндіден іздеу керек.
Келесі теңсіздікті қарастырайық
 (
(
 ) .
) .
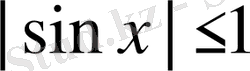 болғандықтан,
болғандықтан,
 болған жағдайда теңсіздіктің шешімі жоқ болады. Егер
болған жағдайда теңсіздіктің шешімі жоқ болады. Егер
 , онда
, онда
 теңсіздігінің көпмүшелігі барлық нақты сандардың көпмүшелігі болады.
теңсіздігінің көпмүшелігі барлық нақты сандардың көпмүшелігі болады.
 болсын. Синус функциясы ең кіші оң периодты
болсын. Синус функциясы ең кіші оң периодты
 қабылдайды, сондықтан
қабылдайды, сондықтан
 теңсіздігінің шешімін алдымен
теңсіздігінің шешімін алдымен
 аралығында іздеу керек. Мысалы
аралығында іздеу керек. Мысалы
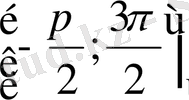 аралығында.
аралығында.
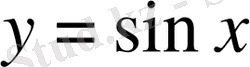 және
және
 (
(
 ) аралығында функцияның графигін құрамыз.
) аралығында функцияның графигін құрамыз.
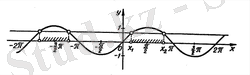
 аралығында синус функциясы өседі және
аралығында синус функциясы өседі және
 , мұндағы
, мұндағы
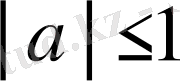 теңдеуінің жалғыз түбірі бар
теңдеуінің жалғыз түбірі бар
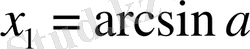 .
.
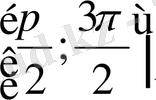 аралығында синус
аралығында синус
функциясы кемиді және
 жалғыз түбірі бар
жалғыз түбірі бар
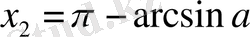 .
.
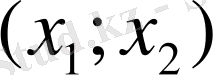 сан аралығында
сан аралығында
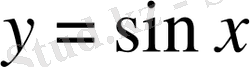 функциясының графигі
функциясының графигі
 графигінен жоғары жатады. Сондықтан
графигінен жоғары жатады. Сондықтан
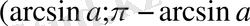 ) аралығындағы барлық х үшін
) аралығындағы барлық х үшін
 орындалады, егер
орындалады, егер
 . Синустың периодтылығы себебінен
. Синустың периодтылығы себебінен
 теңсіздігінің шешімі келесі түрде болады:
теңсіздігінің шешімі келесі түрде болады:
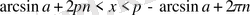 .
.
Сол секілді
 ,
,
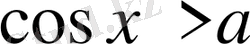 , шешіледі.
, шешіледі.
Мысал1:
теңсіздікті шешіңіз
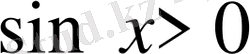 .
.
Шешуі.
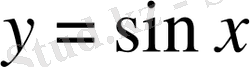 функцияның графигін қарастырайық
функцияның графигін қарастырайық

 осінде
осінде
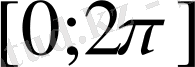 аралығында х мәнін таңдайық, оларға
аралығында х мәнін таңдайық, оларға
 осінен жоғары жатқан нүктелер сәйкес келеді. Ондай аралық
осінен жоғары жатқан нүктелер сәйкес келеді. Ондай аралық
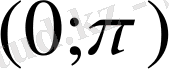 .
.
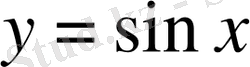 функциясының периодтылығын ескере отырып,
функциясының периодтылығын ескере отырып,
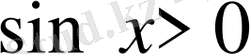 теңсіздігінің барлық шешімін келесі түрде жаза аламыз:
теңсіздігінің барлық шешімін келесі түрде жаза аламыз:
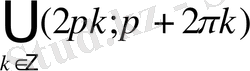 .
.
жауабы.
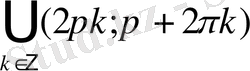 .
.
Мысал2:
теңсіздікті шешіңіз
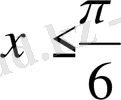 .
.
Шешуі.
 функциясының графигін сызайық. Осы графиктің
функциясының графигін сызайық. Осы графиктің
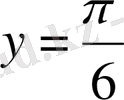 горизонталь функциямен қиылысу нүктесін табамыз.
горизонталь функциямен қиылысу нүктесін табамыз.

Абсциссамен бұл нүкте
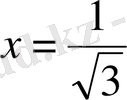 . Графикте барлық
. Графикте барлық
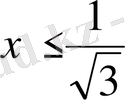 үшін функция графигі
үшін функция графигі
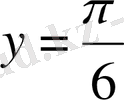 түзуінен төмен жатқанын байқаймыз
түзуінен төмен жатқанын байқаймыз
Жауабы.
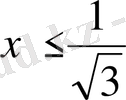 .
.
- Теңсіздіктерді дәлелдеу.
Белгілі бір өрнектерді сан мәндері бойынша бағалау не бір өрнектің екінші өрнектен қандай айырмашылығы бар екенін көрсету т. б себептерден теңсіздіктерді дәлелдеудің қажеттелігі туады.
Алгебралық теңсіздіктерді дәлелдеу әдістерінің барлығы тригонометриялық теңсіздіктерді дәлелдеуге қолданылыны.
1 - мысал:
(1)
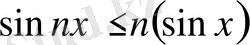 . Мұндағы
. Мұндағы
 (1)
теңсіздікті математикалық индукция әдісімен дәлелдейік.
(1)
теңсіздікті математикалық индукция әдісімен дәлелдейік.
Дәлелдеу:
- oнда
- (1) теңсіздікүшін дұрыс болсын, яғни, (2)
Енді
(1)
теңсіздіктің
 үшін дұрыстығын дәлелдейік. Яғни
(3)
үшін дұрыстығын дәлелдейік. Яғни
(3)
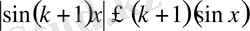 теңсіздігінің дұрыстығын дәлелдейік.
теңсіздігінің дұрыстығын дәлелдейік.

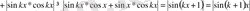 Онда
Онда
 болғандықтан
(1), (2)
теңдіктерден
болғандықтан
(1), (2)
теңдіктерден
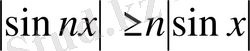
2 - мысал:
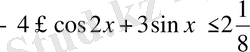 теңсіздікті дәлелдейік.
теңсіздікті дәлелдейік.
Дәлелдеу:
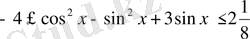
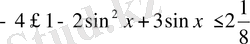
Теңсізідіктің екі бөлігіне де - 1-ді қоссақ
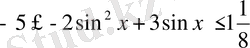
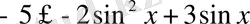 теңсіздігінен
теңсіздігінен
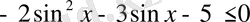 ,
,
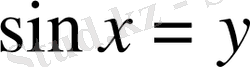 десек
десек
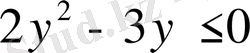 немесе
немесе
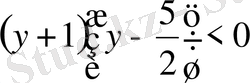
(4 - ті қараңыз) . Бұл арада
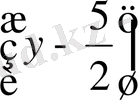 әрқашан да теріс. Ол үшін
әрқашан да теріс. Ол үшін
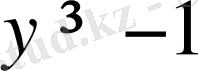 болуы керек, олай болса әуелгі теңсіздік дұрыс. Оң жағы да осылайша дәлелденіледі.
болуы керек, олай болса әуелгі теңсіздік дұрыс. Оң жағы да осылайша дәлелденіледі.
3 - мысал: теңсіздікті дәлелдейік.
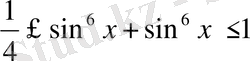
Дәлелдеу:
берілген теңсіздікті
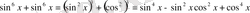 деп жазуға болады.
деп жазуға болады.
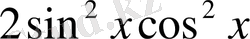 өрнегін
өрнегін
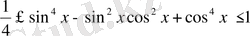 теңсіздігіне қоссақ және алсақ, сонда
теңсіздігіне қоссақ және алсақ, сонда
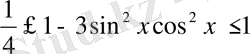 .
.
Теңсіздіктің барлық жағынан 1-ді алсақ
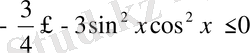 шығады. Теңсіздікті - 3-ке бөліп түрлендірсек,
шығады. Теңсіздікті - 3-ке бөліп түрлендірсек,
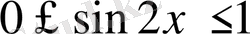 ақиқаттығы белгілі теңсіздік шығады. Олай болса, бастапқы теңсіздік орындалады.
ақиқаттығы белгілі теңсіздік шығады. Олай болса, бастапқы теңсіздік орындалады.
4 - мысал:
теңсіздікті дәлелдейік:
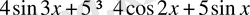
Дәлелдеу:
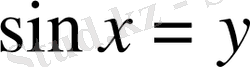 десек, берілген теңсіздікті түрлендірсек
десек, берілген теңсіздікті түрлендірсек
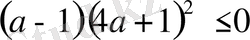 болады. Мұндағы
болады. Мұндағы
 ғана нольден кіші не тең, яғни
ғана нольден кіші не тең, яғни
 . Бұл ақиқаттығы белгілі теңсіздік. Олай болса бастапқы теңсіздік орындалады.
. Бұл ақиқаттығы белгілі теңсіздік. Олай болса бастапқы теңсіздік орындалады.
- Шартты теңсіздіктерді дәлелдеу
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz